Sample Paradoxes Of Decision And Choice Research Paper. Browse other research paper examples and check the list of research paper topics for more inspiration. iResearchNet offers academic assignment help for students all over the world: writing from scratch, editing, proofreading, problem solving, from essays to dissertations, from humanities to STEM. We offer full confidentiality, safe payment, originality, and money-back guarantee. Secure your academic success with our risk-free services.
Choice paradoxes are cases where people make decisions that systematically violate the implications of a theory that is considered (at the time of the ‘paradox’) a viable representation of human decision-making. In the days of the classic paradoxes, a rational person’s choices were thought to be normative and so paradoxes of choice also influenced theoreticians’ ideas of what is rational. Results considered paradoxical from the viewpoint of one theory are explained by newer theories proposed to provide more accurate representations of decision-making. Modern paradoxes are violations of clearly stated premise or implications of a descriptive model.
Academic Writing, Editing, Proofreading, And Problem Solving Services
Get 10% OFF with 24START discount code
1. The Classic Paradoxes
Before 1738, it was considered that a rational person should choose between gambles according to their expected values. The expected value (EV ) of a gamble with n mutually exclusive and exhaustive possible outcomes can be written:
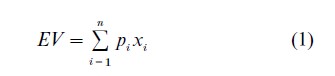
where pi and xi are the probability and prize for outcome i.
1.1 St Petersburg Paradox Refutes EV
The St Petersburg paradox presents a case where scholars insisted that they would and should prefer a small amount of cash to a gamble with much higher EV. Consider the following gamble: a fair coin will be tossed and if the outcome is heads, the prize is $2 and the game ends; however, if it is tails, the coin will be tossed again. If the second toss is then heads, the prize is $4; if tails, the coin is tossed again, and the prize for heads doubles for each successive tails that occurs before heads. When heads occurs, the prize is awarded and the game ends. The EV of this St Petersburg gamble is infinite,
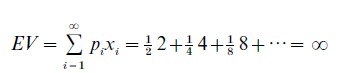
Therefore, if one prefers higher EV, then one should prefer this gamble to any finite amount of cash. Instead, most people say that they would prefer a small sum (e.g., $15) rather than play this gamble once.
1.2 EU Explains St Petersburg Paradox
This paradox, or contradiction between EV and human judgment, was explained by Bernoulli (1738), who showed that if utility is a nonlinear function of wealth, then the expected utility (EU ) of the gamble might indeed be less than the utility of a finite sum of cash. In EU theory:
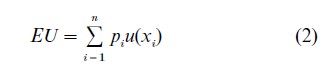
Bernoulli went on to show that EU theory could explain why a pauper might be willing to sell a gamble to a wealthy person for less than its EV and why both would consider the exchange rational. He also explained the purchase and sales of insurance.
When von Neumann and Morgenstern (1947) developed axiomatic foundations of EU and when Savage (1954) developed subjective expected utility theory (SEU), generalizing EU to cases of uncertainty where objective probabilities are unspecified, violations of EV no longer seemed paradoxical. Risk-averse behavior (preferring sure cash over a gamble with the same or higher EV ) and risk-seeking behavior (preferring the gamble over the EV in cash) could be explained by the shapes of the utility functions for different cases. It was not long, however, before new paradoxes were discovered that confounded EU and SEU.
1.3 The Paradoxes Of Allais Violate EU
Allais suggested two-choice problems in which no utility function could be constructed that would explain choices (Allais and Hagen, 1979). The constant consequence paradox is illustrated with the following two choices:
A: $1 million for sure
B: 0.01 probability to win $0
0.89 probability to win $1 million
0.10 probability to win $5 million
A`: 0.89 probability to win $0
0.11 probability to win $1 million
B`: 0.90 probability to win $0
0.10 probability to win $5 million
Choices A versus B and A` versus B` differ only by changing the common consequence on a .89 chance to win $1 million in both sides of the first choice to $0 in the second choice. Many people preferred A to B and also preferred B to A , contrary to EU.
Allais also proposed a constant ratio paradox, which can be illustrated as follows:
C: $3,000 for sure
D: 0.20 probability to win $0
0.80 probability to win $4,000
C`: 0.75 probability to win $0
0.25 probability to win $3,000
D`: 0.80 probability to win $0
0.20 probability to win $4,000
Note that the probability to win is one-fourth in C` versus D`, compared to C versus D. Many people persisted in choosing C over D and D` over C` , contradicting EU theory.
1.4 SEU And The Ellsberg Paradoxes
Consider an option with n mutually exclusive and exhaustive events, where each event, Ei, leads to consequence Ci with subjective probability S(Ei). Savage’s (1954) SEU replaces probability, pi, in Equation 2 with subjective probability, S(Ei).
Although SEU has two subjective functions and may therefore seem hard to test, Ellsberg (1961) devised paradoxes contradicting SEU theory. Ells-berg’s paradox can be illustrated as follows. Suppose there is an urn with 90 balls, 30 of which are Red, and 60 of which are either Blue or Green, in unknown proportion. Now consider Table 1.
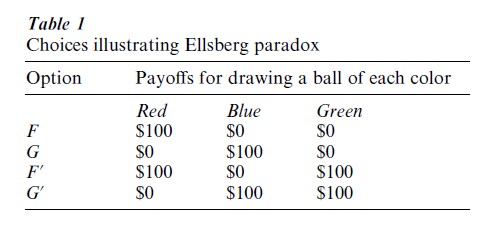
A person who prefers F to G should also prefer F` to G`, since the only difference is the (constant) consequence for a Green ball, which is the same within each choice. If a person prefers F to G, the theory implies that S(Red)>S(Blue), and if that person prefers G` to F` , then S(Red) < S(Blue), a contradiction. In- deed, many people exhibited this paradoxical choice pattern even when confronted with this argument. One interpretation is that people are averse to ambiguity, as well as to risk. Others suggested that the decider might distrust that the urns are identical in both choices.
1.5 Paradoxical Risk Attitudes
In EU theory, the shape of the utility function determines risk attitudes. For example, for x>0, if u(x)=xb, then the person should be risk-averse if b<1, and risk-seeking if b>1. However, many people are both risk-seeking, when p is small, and risk-averse, when p is moderate to large. Furthermore, many people show risk-aversion for small probabilities of heavy losses (they buy insurance) and they accept risks to avoid certain or highly probable losses.
Whereas Allais considered paradoxical choices ‘rational’, and theory to be wrong, Savage considered paradoxical choices to be human ‘errors’ that should be corrected by theory. Many psychologists considered the contradiction between theory and behavior to mean that descriptive theory need not be rational. In this purely descriptive approach, a choice paradox is merely a clear contradiction between theory and human behavior.
Paradoxical risk attitudes and the Allais paradoxes can be described by a theory in which decision weights are a function of probabilities (Edwards 1954, Kahneman and Tversky 1979). Prospect theory (Kahneman and Tversky 1979) described many of the empirical phenomena known by the 1970s. However, this theory was restricted to gambles with no more than two non-zero payoffs and it included a number of seemingly ad hoc editing rules to avoid implications that were considered both irrational and empirically wrong.
2. Modern Theories And Paradoxes
During the 1980s, a number of investigators converged on an approach that used a weighting function of probability but did not have the problems of prospect theory (See reviews by Quiggin 1993, Luce 2000). This class of models includes rank-dependent expected utility (Quiggin 1993), rank- and sign-dependent utility theory (Luce 2000), and cumulative prospect theory (Tversky and Kahneman 1992, Wakker and Tversky 1993, Wu and Gonzalez 1998), among others.
2.1 Rank-Dependent Expected Utility
For gambles with nonnegative consequences, the rank-dependent expected utility (RDEU) of a gamble can be written as follows:
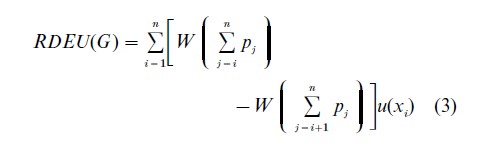
The consequences are ranked such that 0≤x1<x2<x3<…< xn; and W is a strictly mono-tonic weighting function with W(0)=0 and W(1)=1. This representation (and its extensions to the cases of negative outcomes and uncertain events) can handle the classic paradoxes of Allais and Ellsberg.
However, new paradoxes were soon created to test if rank-dependent models are descriptive of choices that people make. The new paradoxes can be analyzed as the result of combinations of simpler properties.
2.2 Transitivity, Monotonicity, Coalescing, And Branch Independence
Transitivity holds if for all gambles, A>B and B>C implies A>C, where A>B denotes A is preferred to B.
Monotonicity assumes that, if one consequence of a gamble is improved, holding everything else in the gamble constant, the gamble’s utility is improved. Coalescing holds that, if two (probability-consequence) branches of a gamble yield the same consequence, then such branches can be combined by adding their probabilities without affecting the gamble’s utility. For example, ($0, 0.8; $100, 0.1; $100, 0.1) ought to have the same utility as ($0, 0.8; $100, 0.2).
Branch independence is the assumption that if two gambles have a common consequence for a given state of the world with known probability, then the value of the consequence on that common branch should have no effect on the preference order induced by other components of the gambles. Branch independence is weaker than Savage’s (1954) ‘sure thing’ axiom be-cause it does not presume coalescing. It was assumed as an editing rule by Kahneman and Tversky (1979).
Let G=(x, p; y, q; z, r) represent the three-outcome gamble to win x with probability p, y with probability q, and z otherwise (r=1-p-q), where 0<x<y<z. For such gambles, restricted branch independence implies,
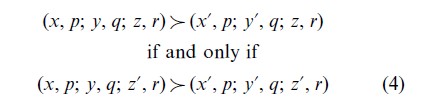
where the branches are distinct, the probabilities are non-zero and they sum to 1. The term ‘restricted’ refers to the constraint that the probabilities and number of outcomes are fixed in all of the gambles. Although branch independence is implied by EV, EU, SEU, and certain other theories, it can be violated by RDEU (equation 3) if the common consequence (z or z`) changes rank. However, if the common consequence maintains the same rank (i.e., the same cumulative probability), the case is termed comonotonic branch independence, which is implied by Eqn. 3.
One can view the constant consequence paradox of Allais as a violation of (noncomonotonic) restricted branch independence, coalescing, and transitivity. Thus, a theory that violates either branch independence (such as RDEU) or coalescing can explain this Allais paradox.
2.3 Paradoxical Violations Of Branch Independence
RDEU (Eqn. (3)) accounts for the observed pattern of risk-seeking for small probabilities to win big prizes and risk-aversion for medium to large probabilities to win modest positive consequences (Tversky and Kahneman 1992). It also accounts for Allais paradoxes if the cumulative weighting function, W in Eqn. (4), has an inverse-S shape (Wu and Gonzalez 1998) in which a probability change near zero or 1 has a greater effect than the same change near 1 2.
However, Birnbaum and McIntosh (1996) reported a pattern of violation of branch independence opposite to the prediction of this inverse-S weighting function. This pattern can be illustrated as follows:
S: 0.80 probability to win $2
0.10 probability to win $40
0.10 probability to win $44
R: 0.80 probability to win $2
0.10 probability to win $10
0.10 probability to win $96
Choices S` and R` differ only in the consequence on the common branch of probability 0.8.
S`: 0.10 probability to win $40
0.10 probability to win $44
0.80 probability to win $110
R`: 0.10 probability to win $12
0.10 probability to win $90
0.80 probability to win $110
According to the inverse-S weighting function, RDEU implies that violations of branch independence should follow a pattern of R>S and S>R . However, the opposite pattern occurs significantly more often than this pattern predicted by the weighting function of RDEU (see review in Birnbaum 1999). Although violations are compatible with Eqn. 3, the observed pattern of violations is the opposite of what was assumed in order to fit Allais paradoxes.
2.4 Configurally Weighted Utility Models
Birnbaum (1997) reviewed configural weight models that he and his colleagues had used in previous research. These models satisfy neither restricted branch independence nor coalescing. They reconcile data that seemed to imply the inverse-S and data that seemed to imply the opposite. Birnbaum’s models and the RDEU class of models (Eqn. (3)) are related by being different special cases of the following configural weight model:
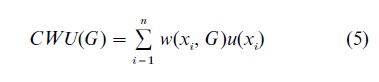
where w(xi, G) is the configural weight of consequence xi in gamble G, and u(x) is the utility function. In the transfer of attention exchange (TAX) model, lower-valued consequences ‘tax’ weight from higher valued ones. A simple version of this model, with u(x)=x for 0<x<$150 has given a good approximation to empirical choices by undergraduates. In this model, the weight of a distinct branch (probability-consequence pair) is proportional to p.7, which is modified by the configural tax. In two-outcome gambles, the lower branch takes 1/3 of the weight of the higher valued branch; in three-outcome gambles, any lower branch takes 1/4 of the weight of any higher-valued branch. Birnbaum (1997) proposed tests between this model and RDEU.
2.5 Paradoxical Violations Of Stochastic Dominance And Event-Splitting
Birnbaum (1997) proposed the following choice:
I: 0.05 probability to win $12
0.05 probability to win $14
0.90 probability to win $96
J: 0.10 probability to win $12
0.05 probability to win $90
0.85 probability to win $96
Gamble I stochastically dominates J because the probability of getting a higher prize than t given gamble I exceeds or equals that of gamble J for all t. EV, EU, and RDEU imply that people should choose I over J. The TAX model, fit to previous data, implies people will choose J.
Birnbaum and Navarrete (1998) tested this pre-diction and found that about 70 percent of college students violated stochastic dominance on this and similar choices, in violation of RDEU. RDEU implies coalescing, monotonicity, and transitivity, so it satisfies stochastic dominance. Configural weight models violate coalescing, and violate stochastic dominance for these cases.
According to the TAX model, it should be possible to eliminate the violations of stochastic dominance by event-splitting, as in the following choice:
IS: 0.05 probability to win $12
0.05 probability to win $14
0.05 probability to win $96
0.85 probability to win $96
JS: 0.05 probability to win $12
0.05 probability to win $12
0.05 probability to win $90
0.85 probability to win $96
Note that IS and JS are simply a split versions of I and J. According to coalescing (and thus RDEU), choices between I and J and between IS and JS are the same. More than half of the undergraduates tested chose J over I and IS over JS, contrary to coalescing (Birnbaum, 1999).
Wu (1994) found violations of tail independence, also called ordinal independence, which can be derived as a combination of coalescing, transitivity, and comonotonic branch independence.
2.6 Violations Of Lower And Upper Cumulative Independence
To characterize the paradoxical relationship between evidence that appeared to imply an inverse-S weighting function and evidence that appeared to contradict it, Birnbaum (1997) deduced two new paradoxes, which he called lower and upper cumulative independence. Consider the following choice:
S: 0.80 probability to win $2
0.10 probability to win $40
0.10 probability to win $44
R: 0.80 probability to win $2
0.10 probability to win $10
0.10 probability to win $98
Now increase the common prize of $2 to $10 on the 0.8 branch of both gambles and coalesce it to the $10 branch in R. Now, increase the consequence of $40 to $44 and coalesce it with the $44 branch on the left. If a person preferred S to R, they should definitely prefer S` to R`:
S`: 0.80 probability to win $10
0.20 probability to win $44
R`: 0.90 probability to win $10
0.10 probability to win $98
However, more people switch preference from S to R` than from R to S`, contrary to monotonicity!
The following choice illustrates upper cumulative independence:
S`: 0.10 probability to win $40
0.10 probability to win $44
0.80 probability to win $110
R`: 0.10 probability to win $10
0.10 probability to win $98
0.80 probability to win $110
If a person prefers R` to S`, then they should prefer R“ to S“:
S“: 0.20 probability to win $40
0.80 probability to win $110
R“: 0.10 probability to win $10
0.90 probability to win $98
Note that the common branch has been reduced in value to $98 in both gambles, but the consequence of $44 has been reduced to $40 in gamble S“, which should make that gamble relatively worse. More people switched from R` to S“ than the opposite (Birnbaum 1999, Birnbaum and Navarrete 1998).
These modern paradoxes, which violate RDEU, were predicted by configural weight models. Undoubtedly, new paradoxes will be developed to confound new theories. Each new finding represents a phenomenon that must be explained by newer theories. Although some are pessimistic that any transitive theory will be able to explain all of the paradoxes, others continue the search for a theory that can explain the widest domain of behavior.
Bibliography:
- Allais M, Hagen O (eds.) 1979 Expected Utility Hypothesis and the Allais Paradox. Reidel, Dordrecht, The Netherlands
- Bernoulli D 1738 Specimen theoriae novae de mensura sortis. Commentarii Academiae Scientiarum Imperialis Petropoli-annae, Vol. 5, pp. 175–92. English translation: Bernoulli D (1954). Exposition of a new theory on the measurement of risk. Econometrica 22: 23–36
- Birnbaum M H 1997 Violations of monotonicity in judgment and decision-making. In: Marley A A J (ed.) Choice, Decision, and Measurement: Essays in honor of R. Duncan Luce. Erlbaum, Mahwah, NJ, pp. 73–100
- Birnbaum M H 1999 Testing critical properties of decision making on the Internet. Psychological Science 10: 399–407
- Birnbaum M H, McIntosh W R 1996 Violations of branch independence in choices between gambles. Organizational Behavior and Human Decision Processes 67: 91–110
- Birnbaum M H, Navarrete J B 1998 Testing descriptive utility theories: Violations of stochastic dominance and cumulative independence. Journal of Risk and Uncertainty 17: 49–78
- Edwards W 1954 The theory of decision making. Psychological Bulletin 51: 380–417
- Ellsberg D 1961 Risk, ambiguity and the Savage axioms. Quarterly Journal of Economics 75: 643–9
- Kahneman D, Tversky A 1979 Prospect theory: An analysis of decision under risk. Econometrica 47: 263–91
- Luce R D 2000 Utility of Gains and Losses: Measurement-theoretical and Experimental Approaches. Erlbaum, Mahwah, NJ
- Quiggin J 1993 Generalized Expected Utility Theory: The Rank-dependent Model. Kluwer, Boston, MA
- Savage L J 1954 The Foundations of Statistics. Wiley, New York Tversky A, Kahneman D 1992 Advances in prospect theory: Cumulative representation of uncertainty. Journal of Risk and Uncertainty 5: 297–323
- von Neumann J, Morgenstern O 1947 Theory of Games and Economic Behavior, 2nd edn. Princeton University Press, Princeton, NJ
- Wakker P, Tversky A 1993 An axiomatization of cumulative prospect theory. Journal of Risk and Uncertainty 7: 147–76
- Wu G 1994 An empirical test of ordinal independence. Journal of Risk and Uncertainty 9: 39–60
- Wu G, Gonzalez R 1998 Common consequence conditions in decision making under risk. Journal of Risk and Uncertainty 16: 115–39




