Partial Orders Research Paper

Formally, a partially ordered set (a poset for short) consists of a pair (P, ≤) where P is a nonempty set and ≤ a binary relation on P satisfying for all x, y, z ϵ P:

(a) reflexivity: x ≤ x,

(b) asymmetry: x ≤ y and y ≤ x implies x = y,

(c) transitivity: x ≤ y and y ≤ z implies x ≤ z.

Transitivity is, in a sense, the most important property; it is shared by all variants of order relations, though it might be a consequence of other conditions. However, asymmetry also contributes in an essential way to the meaning of a partial order. Reflexivity, on the contrary, is merely a matter of taste or convenience. In some cases its opposite, irreflexivity, is postulated. Such an order is called strict. If the asymmetry condition is replaced by symmetry, i.e., for all x, y ϵ Px ≤ y implies y ≤ x, then the resulting structure is an equivalence relation which lacks the interpretation of ‘dominance’ or ‘preference.’ Such a structure is more akin to classification or grouping with respect to similarity.

1. Related Notions And Diagrams

Sometimes asymmetry is simply dropped from the conditions. A relation satisfying reflexivity and transitivity is called a quasiorder. The investigation of quasiorders can be split into the respective properties of a partial order and an equivalence relation in the following way: Let (Q, ≤) denote a quasiorder. Define x ~ y if x ≤ y and y ≤ x both hold true. Then it is readily shown that ~ is an equivalence relation on Q. Let P be the set of equivalence classes and define for p, q ϵ P the relation ≤ by p ≤ q if x ≤ y for some x ϵ p and y ϵ q. Then, one demonstrates two things: first, that the definition of ≤ is independent of the particular elements x ϵ p and y ϵ q; and second, that (P, ≤) is a poset. Thus, the ‘dominance-aspect’ of a quasiorder is contained in ≤, and its ‘classification-aspect’ is hidden in ~.

One property of an intuitive meaning of dominance is not captured in the notion of a partial order: the idea that any two elements can be compared with respect to ≤. The defining conditions of a poset do not imply connectivity, i.e.,

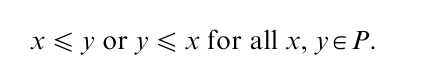
 (Note: often this property is called ‘completeness,’ but later in this research paper another notion of completeness is introduced). If connectivity is added to the properties of a partial order (P, ≤ ), then ≤ is called a linear or total order. A quasiorder satisfying connectivity is called a weak order. Applying the above procedure on a weak order results in a linear order on the equivalence classes of the weak order.

There is a tendency to associate the property of connectivity automatically with an order given in some field of application, e.g., if one rank orders stimuli or subjects. Doing this amounts to representing the order numerically, i.e., to assuming a function

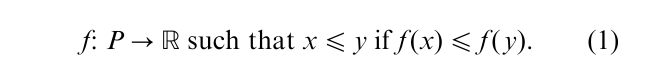
If such a representation is possible, the order is necessarily a weak order. However, in social science, numerical representations are used widely even for orders which cannot easily be justified to be connected. For example, if the items of an achievement test are ‘Rasch-scaled’ (see the discussion following Eqn. (3)), a difficulty coefficient is attached to each item. This numerical scale orders the items weakly and ascribes the often made observation that subjects solve a difficult item correctly and fail at an easier one to influences of chance and error. This interpretation appears so obvious that its proponents tend to overlook the petitio principii which it entails, that the difficulty of an item is defined by the numerical parameter, whereas the weak ordering of the items according to a material notion of difficulty is an empirical property which will in many cases not be fulfilled.

For example, an expert judging this might well regard some items as incomparable. In such a situation a partial(or quasi-)ordering, which allows for incomparable items, is more flexible. Thus, the assignment of numerical values, albeit ubiquitous in psychological tests, restricts drastically the range of possible models. Even partial orders can be too restrictive because transitivity is also a strong condition. The theory of knowledge spaces takes account of this aspect.

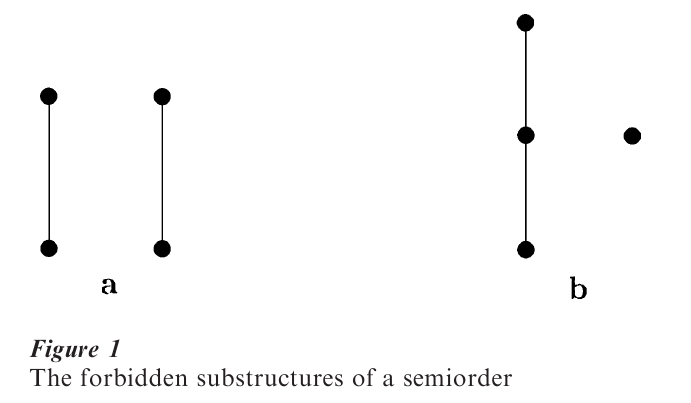
The most convenient way of representing a poset is by its (Hasse) diagram (see Figs. 1 and 2). To construct it, one first defines x < y, in words ‘y covers x,’ to mean: x < z ≤ y implies z = y. Next, one draws a graph in which the vertices correspond to the elements of P, two elements are connected by an edge if one of them covers the other, and furthermore the covering element is placed above the horizontal line determined by the covered element. Hasse diagrams are easy to draw and are of great help in theoretical considerations as well as in interpreting empirical findings.

2. Special Classes Of Orders

There are numerous specializations, that is, additions of further properties, such that the resulting structure is something in between a poset and a linear order. In this section, two classes are considered which have useful numerical representations, although not the strong one of Eqn. (1). The third specialization considered here, namely lattices, is important because it tends to bridge the gap between ordering relations and algebraic operations.

2.1 Semiorders

In psychophysics one has to deal with the phenomenon of subliminal changes in intensity of physical stimuli. One stimulus may be (physically) slightly more intense than another, but a subject does not perceive the difference. For example, one might imagine a coffeetester confronted with an extended series of cups of coffee, each with one more grain of sugar than its immediate predecessor. He/she will probably not notice the difference in taste between successive cups, but surely the difference between the first and the last cup will be clearly noticeable. In other words, indifference with respect to is not transitive. Similar observations can be made in decision theory and other branches of psychology. One way of describing such facts is to introduce sensory thresholds, thereby creating a scaling problem where one wants to scale both the subjective intensity and the magnitude of the threshold. Luce (1956) considered two conditions which seem plausible in this context (P is the set of stimuli and x ≤ y denotes the observation x is less intense than y):

(S1) If x ≤ y and u ≤ v, then x ≤ v or u ≤ y.

(S2) If x ≤ y ≤ z and w ϵ P, then w ≤ z on x ≤ w.

One easily shows that (P, ≤) is a quasiorder, i.e., without losing generality, one can assume that it is a partial order. Condition (S1) says that it does not contain Fig. 1(a) as a suborder. Similarly, condition (S2) is equivalent to the fact that it does not contain Fig. 1(b) as a suborder.

From the viewpoint of measurement the most important property of semiorders is the possibility of a numerical representation with a constant threshold. More precisely, one can show that for a finite semiorder (P, ≤) there is a function f

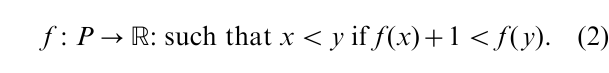
The condition of finiteness is far too restrictive for Eqn. (2), but without further restrictions it does not obtain. The height of the threshold is arbitrary, that is, the number one in Eqn. (2) can be replaced by any other positive number (with a rescaled f ). More on this kind of representation theorem can be found in Roberts (1979, Chap. 6.1) or Suppes et al. (1989, Chap. 16). Clearly, the converse of this theorem is true: a structure with a representation, Eqn. (2) is necessarily a semiorder.

Although the semiorder concept seems to have its origin in the psychological context of the possibility of measurement of subjective intensity described above, it is now a well-established notion in the mathematical theory of posets and several remarkable results are connected with it. Some of them are mentioned in the following text.

2.2 Inter Al Orders

A structure satisfying only condition (S1) but not necessarily (S2) is called an interval order. This notion derives from the numerical representation which is characteristic of this kind of order. Each element can be represented by an interval on the real line and x < y or y < x is tantamount to the nonoverlapping of the respective intervals. Put another way, a scale value and a threshold are attached to each element, but the height of the threshold can vary in contrast to Eqn. (2). The reader will find many interesting properties and proofs in Fishburn (1985).

Historically, it is of interest that, although the representation theorem is due to Fishburn (1970), the investigation of this structure goes back to papers of Norbert Wiener, early, in the twentieth century. What is even more remarkable is that in this work he mentioned possible applications in experimental psychology (see Fishburn and Monjardet 1992).

The theory of interval orders has applications in archeology in connection with the seriation problem. In this case P is a set of artifacts, each element of which was some time in use. From excavations in various historical sites it is known for any two artifacts whether the period of use of one follows that of another with or without overlap. If this relation satisfies (S1) then, by the interval order representation theorem, it follows that it is possible to assign a time interval to each artifact, preserving the empirical observations.

A related notion is that of a biorder. The primitives of a biorder consist of two sets P and Q and a relation ρ between P and Q, i.e., a subset ρ C P × Q satisfying for all x, y ϵ P and u, v ϵ Q

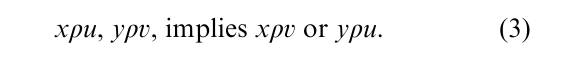
To understand this condition, it is helpful to think of P as a set of subjects and of Q as the items of an achievement test. xρu means ‘subject x fails to solve item u.’ The premise of Eqn. (3) says that x fails u and y fails u: if one assumes that x solves correctly, then y has to fail u. With this interpretation, the biorder concept is the basis of Guttman scaling. Probabilistic modifications of it underly Rasch scaling, which is well-established in the theory of psychological tests. Thus, with the biorder condition Eqn. (3), a testable property is formulated which, when satisfied, justifies a numerical difficulty value for items because a numerical representation of a biorder consists of two functions f: P → R and g: Q → R such that:

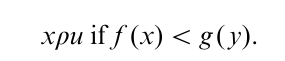
This, in turn, implies Eqn. (3). In the terminology of the above interpretation of a biorder f (x) is the ability of subject x and g (u) is the difficulty of item u. If in a biorder, the two sets coincide, P = Q, then Eqn. (3) reduces to (S1), i.e., the structure is an interval order.

2.3 Lattices

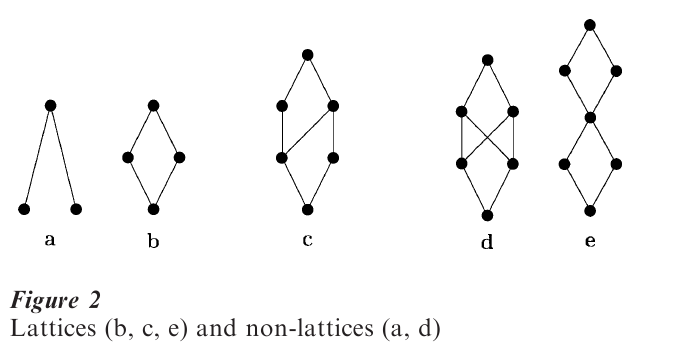
In a partial order (P, ≤) subsets of P may or may not have upper or lower bounds, where upper bounds are elements which dominate all elements of the subset and lower bounds are elements which are dominated by all its elements. If each two-element subset has a unique smallest upper bound—called the supremum— and a unique greatest lower bound—called the infimum—then the structure is called a lattice. The infimum of x and y is denoted by x ^ y and the supremum by x v y. Examples of lattices and nonlattices are given in Fig. 2.

Further examples are the power set of a set ordered by set inclusion, any subset of the reals naturally ordered, and the natural numbers {1,2,3, …} ordered by divisibility, i.e., m ≤ n if m divides n. In the last example, the least common multiple and the greatest common divisor are the supremum and the infimum, respectively. It follows easily by induction that any finite subset of a lattice P has an infimum and a supremum. However, infinite subsets do not necessarily have this property. If all subsets of P have it, then the lattice is called complete. Thus, finite lattices are always complete, but the rationals with the natural ordering are not. The question of completion of lattices similar to the construction of the reals by Dedekind cuts is discussed in Sect. 5.

There is a more algebraic way of characterizing lattices, where infimum and supremum are regarded as binary operations on P:

Theorem 1 Let ( P, ≤) be a lattice. Then for all x, y, z ϵ P:

(a) x v ( y v x) = (x v y) v z and x ^ ( y ^ z) = (x ^ y) ^ z

(b) x v y = y v x and x ^ y = y ^ x

(c) x ^ (x v y) = x and x v (x ^ y) = x.

Conversely, if a structure ( P, v, ^) is given with operations v, ^ satisfying the conditions (a), (b), and (c), then ≤ is defined by

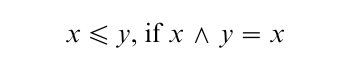
is a partial order on P such that ( P, ≤) is a lattice. Lattices play an important role in pure and applied

mathematics. John von Neumann, one of founders of lattice theory, developed his formulation of quantum mechanics in terms of lattices. Today they are used in many branches of mathematics—for instance, in combinatories, probability theory, logic, and functional analysis. The wide applicability of lattices in technical and social science contexts is best demonstrated by the development of ‘concept analysis’ by Rudolf Wille (see Ganter and Wille (1996).

3. Extension Of Orders; Szpilrajn’s Theorem

Is it possible to extend a partial order by adding (x, y) or (y, x) to ≤, when x and y are incomparable in ≤ and at the same time keeping the extended relation a partial order? Is it possible to extend ≤ to a linear order in this way? Both questions are answered in the affirmative by the following theorem.

Theorem 2 (Szpilrajn’s Theorem) Let (P, ≤) be a poset and x, y ϵ P such that neither x ≤ y nor y ≤ x. Then there are two linear orders ≤´ and ≤´´, each of which contains ≤ as a subset, and such that x ≤´ y and y ≤´´ x.

The proof of this theorem is not difficult for finite P, but entails a set theoretic twist in the infinite case. If x and y are incomparable in ≤ then one defines x ≤´ y, adds all pairs to ≤´ which this choice and transitivity forces and goes ahead until no incomparable pairs are left over. The latter step of this argument is a bit of a problem for an infinite P.

Sometimes one can regard a partial order as ensuing from incomplete data collection, incomplete in so far as a linear order can be expected, but the available data give only a part of the full order information. Then the question of a linear extension is relevant, in particular, one can ask how many additional pairwise comparisons must be performed to obtain the full linear order, which is the most parsimonious way to find such an extension.

For these problems the number of linear extensions is of importance. It was shown by Fishburn and Trotter (1992) that for all partial orders with fixed |P| = n and k pairs in ≤ those with a maximal number of linear extensions are semiorders. For k ≤ n these semiorders are characterized, but for larger K there seem to remain several unsolved problems.

It can be shown that a linear extension can be found with at most K questions of the form ‘is x larger than y,’ where K is of the magnitude of the logarithm of the number of linear extensions (see Trotter 1995 for details). In connection with this problem it seems that a pair x, y for which many extensions with x ≤ y, as well as many with y ≤ x exist is best to investigate first because, whatever the answer, it considerably reduces the number of data which remain to be collected. In this context the so called 1/3–2/3 conjecture was made. It says that each poset which is not a linear order contains a pair (x, y) for which the relative frequency of extensions with x ≤ y is between 1/3 and 2/3. This conjecture seems still open. However, bounds are known, e.g., the relative frequency is between 3/11 and 8/11. The proof of this result draws on a geometric inequality and is extremely beautiful. For semiorders the 1/3–2/3 conjecture is true. More on this topic and some of the proofs can be found in Trotter (1995).

4. Order Dimension

A corollary of Szpilrajn’s Theorem is that each partial order is the intersection of its linear extensions. One can ask for the minimal number of linear extensions with this property and regard this number as a measure of complexity of the order. It is called the dimension of (P, ≤).

All orders on three, four, and five elements are two- dimensional (provided they are not linear). There are two orders with six elements of dimension three. One can group the posets in classes of increasing dimension. The semiorders have a dimension less than or equal to three, but the interval orders can have arbitrary large dimension.

One classical result on the dimension is that it is always smaller than or equal to the maximal number of pairwise incomparable elements. For |P| ≥ 4 ( |P| denotes the number of elements in P) the dimension is bounded above by |P|/2 and this is the best possible solution. It is an active area of research to find inequalities such as these which relate the dimension to other characteristics of the poset (see Trotter (1992)).

There are other variants of the dimension concept: one can replace linear orders by semiorders (and obtain the semiorder dimension) or by interval orders or by any other class of partial orders. For biorders, see Doignon et al. (1984) and Koppen (1987). These two papers attempt to link this dimension concept to techniques of extracting factors to explain data. In this way, an ordinal factor analysis is outlined. Factor analytic procedures used to be widely spread in social science research, but until now they seem to lack a sound axiomatic foundation. The order theoretic dimension concept can provide a weaker concept of a factor which is, on the other hand, much easier to justify, or empirically to test for adequacy.

5. Embeddability And Completion Of Orders

Sometimes the nonexistence of suprema and infima is a nuisance; just think of the inconvenience caused when a sequence of rational numbers ‘converges,’ but the limit does not exist (in the rationals). One tries to avoid this situation by embedding a given poset into a complete lattice which contains the original order as a suborder. In contrast to the techniques in Sect. 3, one adds new elements to P instead of new pairs to ≤. Thus, the aim is to find a superstructure which resembles the given order as closely as possible, but which can be handled more conveniently because of the existence of suprema and infima. The prototype of this kind of extension is the time-honored construction of the reals from the rational numbers.

To begin with, some notation must be introduced. For X C P let:

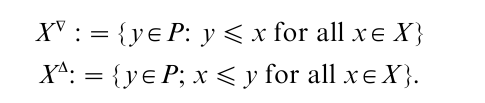
Thus X^∆ is the set of lower bounds of X and X^∆ the set of upper bounds of X. The sets {x}^∆ and {x}^∆ for x ϵ P are abbreviated by x^∆ and x^∆, respectively. One simple way of embedding consists of considering

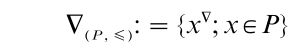
the so called principal ideal representation. Note that ( ∆ _(P,≤), C ), is a suborder of the complete lattice of the power set, isomorphic to (P, ≤). However, this embedding is not sufficient for the purposes of this section; the superstructure carries too little information from the original one. Therefore, a more parsimonious extension must be constructed.

To this end, a pair (X, Y ) is called a MacNeille cut if and only if X = Y^∆ and Y = X∆. The set of all MacNeille cuts is a better candidate for an embedding. Indeed, one can prove:

Theorem 3 Denote by C_(P,≤) MacNeille cuts of a partial order (P, ≤). Define for two cuts (X, Y ) and (X´, Y´) the relation

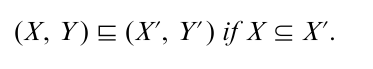
Then (C_{(P, ≤ )}, C ) is a complete lattice. Moreover, it is the unique (up to isomorphism) smallest complete lattice which contains the original poset (P, ≤) as a supremum dense subset, i.e., each element of C(P, ≤) is supremum of elements of (P, ≤).

A few remarks should illustrate this theorem. First, the set corresponding to (P, ≤) in (C_{(P, ≤)}, C ) is the set of cuts (x^∆, x^∆). Second, if this theorem is applied to the rationals with the usual (linear) order, then the reals with added {-∞} and {∞} result as the MacNeille completion. The element -∞ is the cut ( 0, P) while ∞ is the cut (P,0). Third, although the notion of a complete lattice only bears meaning for infinite base sets P, the MacNeille completion makes sense also for finite posets. Figure 2(b) shows the MacNeille completion of (a) and Fig. 2(e) of (d). Finally, it is worth mentioning that the mappings X → X^∆ and X → X^∆ form a pair of functions that are known as a Galois connection. This construction is often used when dealing with posets; it is applicable in other contexts, for example, formal concept analysis (see Ganter and Wille (1996) is based on a Galois connection). In this respect, concept lattices are a generalization of a MacNeille completion.

Bibliography:

1. Doignon J-C, Ducamp A, Falmagne J-C 1984 On realizable biorders and the biorder dimension of a relation. Journal of Mathematical Psychology 28: 73–109
2. Fishburn P C 1970 Intransitive indifference with unequal indifference intervals. Journal of Mathematical Psychology 7: 144–9
3. Fishburn P C 1985 Inter al Orders and Inter al Graphs. Wiley, New York
4. Fishburn P C, Monjardet B 1992 Norbert Wiener on the theory of measurement (1914, 1915, 1921). Journal of Mathematical Psychology 36: 165–84
5. Fishburn P C, Trotter W T 1992 Linear extensions of semiorders: A maximization problem. Discrete Mathematics 103: 25–40
6. Ganter B, Wille R 1996 Formale Begriff Springer, Berlin
7. Koppen M G M 1987 On finding the bidimension of a relation. Journal of Mathematical Psychology 31: 155–78
8. Luce R D 1956 Semiorders and a theory of utility discrimination. Econometrica 24: 178–91
9. Roberts F S 1979 Measurement Theory with Applications to Decision-making, Utility, and the Social Sciences. AddisonWesley, Reading, MA
10. Suppes P, Krantz D H, Luce R D, Tversky A 1989 Foundations of Measurement, Vol. 2: Geometrical, Threshold, and Probabilistic Representations. Academic Press, New York
11. Trotter W T 1992 Combinatories and Partially Ordered Sets: Dimension Theory. Johns Hopkins University Press, Baltimore, MD
12. Trotter W T 1995 Partially ordered sets. In: Graham R L, Grotschel M, Lovasz L (eds.) Handbook of Combinatories. Elsevier, Amsterdam, pp. 433–80