Sample Problem Solving And Analogical Reasoning Research Paper. Browse other research paper examples and check the list of research paper topics for more inspiration. If you need a religion research paper written according to all the academic standards, you can always turn to our experienced writers for help. This is how your paper can get an A! Feel free to contact our research paper writing service for professional assistance. We offer high-quality assignments for reasonable rates.
1. The Closing Of Gaps In Human Problem Solving
Deduction, induction, and analogical reasoning, the three basic forms of logical thought, were derived from natural or everyday situations, where they were originally embedded in commonplace forms of interaction and communication. The differences are explained in the respective paragraphs.
Academic Writing, Editing, Proofreading, And Problem Solving Services
Get 10% OFF with 24START discount code
Depending on the context, the German word ‘schließen’ (‘conclusion’) may mean to ‘close,’ ‘conclude,’ ‘reason,’ or ‘infer.’ Generally speaking, the term implies the bridging or closing of a gap, be this a literal gap between two entities or, in the metaphorical sense, a logical gap between a problem and its solution. The closing of such metaphorical gaps by means of reasoning or inference usually entails a series of cognitive ‘steps.’
Problems can be defined in terms of three characteristic stages: (a) an initial state (e.g., the arrangement of the figures on a chess board, an algebra or geometry exercise, or a balance of trade), (b) an end state (e.g., putting the opponent’s king in checkmate, solving the maths exercise, or finding ways of improving the balance of trade), and (c) a well-defined series of cognitive ‘steps’ by which the initial state is trans-formed to the end state: the solution to the problem (or one of a number of solutions).
They are still to be found in their original, undifferentiated form as IF-THEN relations: in barter, trade, the manufacture of implements, and the planning of collective action, for example. Once raised to the metalevel of pure thought, these forms of reasoning became a subject of philosophical inquiry in the fields of mathematical logic, linguistics, and psychology. Over the course of history they even became independent areas of scientific systematics. It was only at a very late stage, in the time of the great Greek philosophers, that the three types were differentiated, defined, and each traced back to its logical structure. This represented the first step on the path to European or Western thought and the scientific advances that were entailed. And the first to tread this path were the great trio of Ancient Greek thought—Socrates, Plato, and Aristotle.
2. Three Great Greek Philosophers And The Foundations Of Logic
In the early Socratic Dialogues—preserved in Plato’s writings—the processes of reasoning are dominated by IF-THEN relations. These and other dialogues demonstrate the inevitability of human thought. When we are told that all men are mortal and that Socrates is a man, our cognitive processes preclude us from harboring any doubts that Socrates is mortal. We will return to this aspect. First, it should be noted that this kind of logic is not rooted in words. It was one of Plato’s fundamental theories that the objects perceived by the senses are but imperfect copies of Ideas, the mental representations now known as concepts. Socrates had already used inductive arguments to formulate definitions of concepts by gradually identifying their characteristic properties or features. Regardless of the countless possible variations in the shape perceived as a triangle, for example, the sum of the angles must always be equal to two right angles, and half the product of baseline and height must always be equal to the area. This is Plato’s concept—or Idea—of triangularity.
By applying the principle of dieresis—the breaking down of a concept into ever more narrowly defined subconcepts—Plato developed a general taxonomy of concepts and a system of concept-subconcept relations. This laid the foundation for the Aristotelian system of classification: first the broad general category (genus proximum), then the more specific (differentia specifica)—for example, a tree is a plant with branches and leaves or needles.
In his treatise On Interpretation, Aristotle stripped away the semantic content of propositions, revealing the comparable structures behind the words. ‘First we must define the terms ‘‘noun’’ and ‘‘verb,’’ then the terms ‘‘denial’’ and ‘‘affirmation,’’ then ‘‘proposition’’ and ‘‘sentence.’’ Spoken words are the symbols of mental experience and written words are the symbols of spoken words.’ It was another 2000 years before Wittgenstein again addressed this issue in such clear terms. Aristotle’s approach enabled him to formulate the figures of classical logic, the syllogisms. His theory of syllogistic reasoning drew on Plato’s hierarchical ordering of concepts, and a syllogism was defined as ‘discourse in which, certain things being stated, something other than what is stated follows of necessity from their being so.’ A well-known example is the syllogism: A is true of all Bs. C is an A. Therefore, B is true of C. ‘All humans are mortal. Socrates is a human. Therefore, Socrates is mortal.’ Negation operates on similar lines: ‘No self-luminous bodies are planets. All fixed stars are self-luminous. Therefore, no fixed stars are planets.’ These syllogisms were central to philosophical and logical inquiry throughout the Middle Ages and on into modern times.
Although examples with natural terms were mainly used to analyse and dispute the universality of the logical structures, it was not until 1679–90 that a new level of knowledge was attained in the field of logic. Scholars began to ask which inferences can be made when the premises of an argument are derived from prior experience, and do not allow universally valid conclusions to be drawn. This question was first formulated in clear terms by Gottfried Wilhelm Leibniz. Leibniz envisaged a universal formalized language, a ‘Mathesis universalis,’ for the general analysis and description of human knowledge, a kind of algebraic representation of logical reasoning in human thought. The system was to encompass even those cases in which the given circumstances and available data did not allow definitive conclusions to be drawn. Leibniz suggested calculating the degree of probability that a logical conclusion would be reliable. Bolzano (1970) followed this line of thought, postulating that the prediction of a conclusion is governed by the conditions of occurrence in a sequence of events. This approaches the twentieth century definition of probability as the likelihood of an event. These are examples from an era in which the ground was prepared for a new method for acquiring the precise definition of inductive reasoning.
3. Drawing Conclusions From Insufficient Information: Induction
Inductive reasoning occurs when a conclusion does not follow necessarily from the available information. As such, the truth of the conclusion cannot be guaranteed. Rather, a particular outcome is inferred from data about an observed sample B´, {B´} c {B}, where B means the entire population. That is, on the basis of observations about the sample B´, a prediction is made about the entire population B. For example: Smoking increases the risk of cancer. Mr X smokes. How probable is it that Mr X will develop cancer? As this example illustrates, inferential statistics (t-tests, analyses of variance, and other derived forms) are based on this kind of inductive reasoning.
The problems associated with the use of induction in scientific reasoning have been addressed from both philosophical and the mathematical perspective. From the philosophical point of view, the question arises as to what this process—the drawing of universal conclusions about a given phenomenon on the basis of the probability in a simple—actually entails. Logicians, as we now discuss, have responded in a variety of ways (v. Mises, Reichenbach, Keynes, Jeffrey, and Carnap).
Carnap’s influential approach to this issue represents a form of compromise. Carnap calculates probability on the basis of accumulated experiential data, where confirmations of one hypothesis as opposed to another are entered into the equation as weights, basically resulting in a kind of weighted mean.
4. Psychological Assumptions From Bayes’ Theorem
In psychological research (artificial or experimental) many attempts have been made to analyse beliefs about probability on the basis of examples. For example, marbles are randomly selected from a jar containing an unknown number of red and black marbles, and study participants asked to predict the next color to be drawn. Participants’ predictions are sometimes based on a priori probabilities, i.e., unconditional, fixed relative frequencies. In central Europe, for example, the probability that it will rain in July is very high; the probability that it will snow is very low. These predictions would have to be modified for the month of April, and may even have to be reversed for January. Everyday human decision-making is rarely determined by such absolute probabilities however. This can be illustrated by the example of a horse-racing enthusiast’s gambling behavior. Let us assume that the gambler is familiar with the horses taking part in the race and decides to bet that the favorite, horse E, will win. He goes to the tote and sees that horse E is injured and will not be taking part in the race. Our gambler immediately modifies his predictions, selecting the second favorite from the list of starters and placing a bet on this horse instead. This is not necessarily the horse he had previously predicted would come second, however. He might even decide not to bet on second place. Either way, his decisions are still based on estimates of probability, but as a result of the change in circumstances there are now fewer possible choices available. This points to the conditioned probabilities. The hypothesis set H for the decision H (horse E) has been reduced by the conditional probability p(E H). This can be seen in relation to the probability of the alternative hypothesis.
In calculating the so-called a posteriori probability, a comparison is drawn between these two quantities. p(E|H) is weighted with the a priori probability:
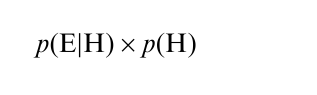
This is then placed in relation to the set of all possible positive or negative outcomes according to probability, resulting in the theorem named after Thomas Bayes:
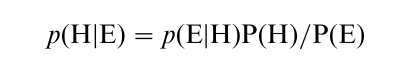
Many experiments in the field of psychology (see Gluck and Bower 1988) have been conducted to test whether the a posteriori probability is indeed as effective in human decision-making behavior as this calculation suggests. While some findings confirm the effectiveness of these components, some significant deviations from the theorem have also been registered. These deviations have provided important psychological insights, however. Edwards and Schmidt (1966), for example, conducted in-depth investigations into the ways people adapt their estimates and decision-making behaviour to the changed circumstances when the given information is modified—H-D Schmidt on the basis of high-risk hits of balls, Edwards using gaming chips and estimates of chance. Both found high levels of interindividual variation in the adaptability of study participants. While some people are flexible with respect to their predictions, many others—the so-called ‘conservative estimators’—try to retain their initial predictions for as long as possible.
The findings reported by Kahnemann and Tversky (1973) are also very interesting in this context. They found that study participants largely ignore a priori probabilities in their predictions of specified variables, preferring to orientate themselves to conditional probabilities. This result is not counterintuitive, as the conditional probabilities are the most salient. The so-called Monte Carlo effect is another example of the insensitivity to a priori probabilities. Suppose that marbles are drawn with replacement from an urn containing an equal number of red and black marbles. The probability of randomly drawing a marble of either colour is 50 percent. If a red marble has been drawn on a number of consecutive occasions, however, study participants regularly predict that it is more likely that a black marble will be selected next. They overlook the fact that each draw is an independent event, and that the a priori probability is independent of the previous draws, i.e., remains constant at 50 percent.
In a fictitious diagnosis experiment, Gluck and Bower (1988) found a high level of correspondence between the estimates made by study participants and the odds calculated using Bayes’ formula. On the basis of a medical chart, study participants were asked to judge which of two diseases their (hypothetical) patients were suffering from. The a priori probability of one of the diseases was three times higher than that of the other. The conditional probabilities were then varied by the listing of symptoms relevant to the diagnosis. Gluck and Bower found a high degree of correspondence with the Bayes’ calculations. When asked to estimate the frequency with which a symptom is associated with one of the two diseases (the rarer one), however, the study participants were unable to make reliable predictions. Hence, the ‘diagnosticians’ came to a Bayesian conclusion without using Bayesian methods. Gluck and Bower refer to this as implicit knowledge.
5. Implicit Knowledge In Reasoning
The question remains of how such a data compilation functions on the cognitive level. It can be assumed that such processes involve the compression of accessible information and that they are of a non-algebraic character. They constitute abstractions about data sets, leading to a kind of blurred conceptual knowledge. Examination of the effects of quantifiers in logical arguments has provided insights into these processes. The modus ponens is quite categorical: If P, then A holds. In other words, P implies (→) A. Given P then A, hence P → A. If it rains (P), then the lawn will be wet (A). It has rained, therefore the lawn is wet; P → A. Is the reverse (not P) also true? That is: ⌐ P →⌐ A? Not necessarily; the lawn may well have been watered with a sprinkler or a hosepipe. It has been shown that, in more abstract contexts, even adults have difficulties in understanding this so-called modus tollens (Wason and Johnson-Laird 1972). But does the modus ponens also hold for conclusions beginning with the quantifier ‘some’? For instance does it follow from ‘some As are Bs, and some Bs are Cs,’ that, ‘some As are Cs’? Not necessarily. For instance, substituting ‘women’ for As, ‘doctors’ for Bs and ‘men’ for Cs, we would arrive at the conclusion that some women are men. Alternatively, assuming that some Bs are As and some Cs are Bs, does it follow that some As are Cs? Again, this is not entirely true, as is immediately apparent when terms from natural language are entered into the equation (cf. Anderson). Wason and Johnson-Laird (1972) have investigated the acceptance of such logical arguments in detail. Cosmides and Tooby (cf. Horgan 1995) have attempted to provide an explanation, postulating that such halo effects on techniques acquired over the course of evolution help to reap the maximum benefits. For example, they suggest that the need to detect deception on the part of one’s interactants is an essential incentive for the development of human intelligence. The well-known prisoner’s dilemma is another such phenomenon. At issue here is whether players trust in the other player having a positive attitude to sharing, or whether they attempt to appropriate the entire winnings at the risk of losing everything. There is no doubt that the maximum-benefit motive plays a role in numerous decision-making processes. In general, however, the evolutionary influences on logically motivated decision-making behavior are located at a deeper level—in strategies which remain stable over the course of evolution and account for both individual and group interests. And not only in the sense of reaping the maximum social benefits. The so-called Monte Carlo effect (see earlier discussion) is but one example. Since time immemorial, humans have experienced that even prolonged natural processes such as weathering, drought, rain, floods, epidemics, disease, etc. eventually come to an end. And it generally holds that the longer these processes have been operating, the more imminent (i.e., the more probable) their conclusion. Such an approach appears to be the heritage of experiences gathered over the thousands of years of hominid history. The fact that humans prefer to extrapolate to the future—as implied by the modus ponens with its deterministic IF-THEN relations—is a favorable predisposition, increasing the chances of survival. It is very simple: It is more important to react to potential future events than to past occurrences. As there is only limited storage space in a modular nervous system, some bodies of knowledge become overgeneralized, perhaps as a result of being classified in line with the modus ponens. A similar pattern emerges for the weaker inductions of the modus tollens: In order to behave appropriately in one’s environment, it is less important to know what can be inferred about the antecedent conditions from the absence of an event than vice versa.
6. Reasoning And Analogies
While deductive reasoning, in logic, refers to the necessary outcomes of a set of conditions, inductive reasoning is concerned with determining the likelihood of an outcome. Only possible conclusions can be drawn, since not all of the conditions influencing or determining the outcome of a given situation are known. Analogical reasoning has a different character; it is basically a more precise form of conjecture. It is based on the mapping of structures or relations valid in one domain of knowledge onto another—less familiar or unknown—domain. The structures to be mapped are selected on the grounds of the similarity between the novel problem and the familiar one. The novel area is defined as the target domain of analogy construction, the familiar area as the source domain. With respect to the truth values of the conclusion, analogical reasoning spans all variants—from the absolute certainty of the modus ponens to a posteriori probabilities according to Bayes’ Theorem, some of which are very weak. Suppose, for example, a second pair of terms is sought for a pair of numbers such as 3: 6. Pairs such as 8: 16 and 64: 128 among many other combinations meet the requirements of the analogy.
As shown in Fig. 1, analogy construction can also be applied to geometric figures. It may be, but does not have to be the same factor of horizontal stretch which is mapped to produce a rectangle from a square or an oval from a circle. The boundaries within which geometric analogies are accepted are fuzzy, but when these boundaries are overstepped, the analogies are rejected. The same holds for meaningful words in natural languages. Let us imagine that analogous pairs with the same relational correspondence are to be generated for the following pairs of words: (a) collie: dog, (b) walk: run, (c) oak: birch. A good number of satisfactory analogies can be found, for example: (a) rose: flower, (b) speak: shout, (c) carp: trout. In each pair, the first term has all the relevant properties of the second (animal, voice, plant), as well as some of its own. The first pair is characterized by a sub-superconcept relation, the second by the intensity of the characteristic feature (the semantic relation of the comparative). The third pair shares a super-concept with common properties, but each term has specific properties of its own (the semantic relation of coordination). Pairs of terms such as dress and bullet or flea and fog do not allow analogies to be drawn on the basis of common properties, as these are non-existent. Clearly, similarity between the terms is an integral element in the construction of analogies. This similarity is not necessarily rooted in common properties, however. For us pairs of terms such as (a) ship and ocean, (b) hunter and deer, and (c) surgeon and scalpel, for example, do not share common properties. Nevertheless, the relational connections between the concepts are comparable with those found in other pairs of terms. In example (a) the shared relational connection is the location (as in flower and garden), in (b) it is the object of the action (as in butcher and cow), and in (c) the instrument (as in farmer and scythe). More complex relations can also be involved, as in ‘learn: know’ paired with ‘fight: win.’ Here, the common semantic relation is the objective or purpose. Such relational connections are the basis for analogy construction: ‘The shark is the wolf of the ocean,’ for example, or ‘May is the Mozart of the calendar’ (Erich Kastner). Many such examples are to be found in the Bible, particularly in the parables of the New Testament.
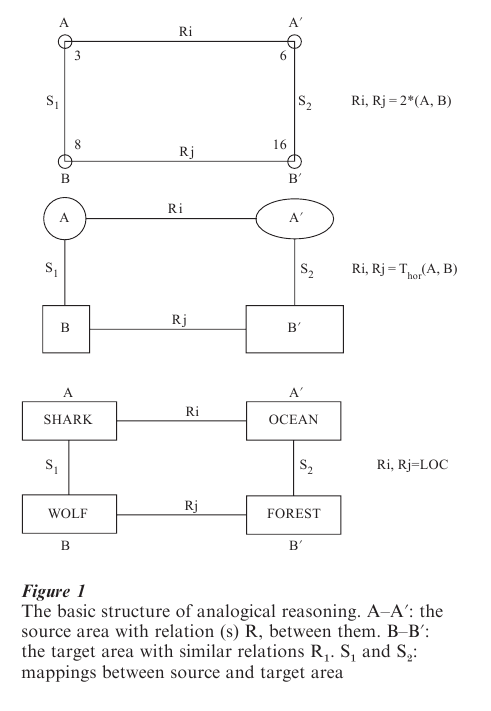
7. The Origins And Original Function Of Analogies
Analogies are evidently not isolated examples of mental games, but a constant cognitive law. But what is the point of these transfers between bodies of knowledge? Is it just a case of juggling with combinations of words that match in some way? Or do analogies reflect a deeper (perhaps even social) need of Homo sapiens? Viewed from this evolutionary perspective, the question arises of where, exactly, the origins of analogical thought are to be found.
Analogical thought is primarily to be found in language use. Indeed, the key word ‘language’ puts us on the right track, for the evolutionary origins of analogy are rooted in the need to communicate, and similes and metaphors are its direct evolutionary source. The cognitive function of analogy is to facilitate discourse; when an interiocutor does not understand a particular term or statement, the speaker attempts to clarify its meaning. This he or she does by referring to common knowledge that is as similar as possible to the term or statement in question. Similes and metaphors are essential ingredients of this procedure. The comparative phrase ‘is like’ is often added as an explicit reference to the existing similarity (Rumelhart 1979). For example, it is quite possible to imagine the following explanation being given in the course of prehistoric dialog:
Question: ‘What’s a quagmire?’
Answer: ‘It’s like a trap in the mud.’
The second term functions as a source of new knowledge. Indeed, the very purpose of this dialog is to impart (or acquire) new knowledge. This is also the case when adults explain things to children: ‘The heart is like a motor driving the body,’ ‘pathologists are like butchers,’ or ‘rules are like corsets,’ for example. Complete analogies can be viewed as extensions of such metaphors—for example, ‘Rock in the opera— that’s like heavy metal in cathedral,’ an executioner in the Salvation Army is like a monk in the artillery,’ or ‘a June meadow in the mountains is like a bride in her wedding dress.’ The list is never-ending. Such examples are no longer explanations or supplements to existing knowledge, but this is the source from which they originated. And, as illustrated by Eichendorff reference, they display originality and creativity of thought: ‘It was as if the Sky had silently kissed the Earth, so that she, in the glimmer of blossoms, now had to dream of him.’ A somewhat more mundane example can be drawn from one of General Moltke’s cadet examinations. When Moltke asked a cadet, ‘How wide is the Thames in Paris?,’ the boy replied, ‘Just as wide as the Seine in London, your Excellency.’ By inverting the terms, the cadet demonstrated that he was well aware of the existing relations. Analogies can thus also be a source of smiles and approval.
8. Cognitive Procedures In Analogy Construction
Without a doubt, the recognition of structural similarities between the source and target domains plays a pivotal role in the acceptance of proposed analogies, as well as in their completion (e.g., supplying a fourth term when three are given), and creation (suggesting a new and possibly unique second pair of terms). Similarity is a necessary precondition in all three cases.
Different approaches to the definition of conceptual similarity have emerged in the literature definition in terms of (a) shared conceptual properties, as proposed primarily by Tversky Lit. and (b) structural similarity, as suggested by Gentner and Stevens (1983). A compromise between these two approaches has been formulated by Bachmann (1989) after Jaccard and Tanimoto.
Tversky defines the similarity between two objects in terms of the relationship between the features common to both structures and the features distinct to each, be they perceptual structures or sets of conceptual properties. As in Tversky’s experiment, both components were then aggregated and compared to the estimated values. This resulted in a significant improvement on the correspondence between feature overlap and estimated similarity. The degree of improvement varied from concept, but correspondence calculated on the basis of common features alone was significantly lower.
The weighting on each of the semantic relations in similarity judgments is another matter of interest, and can be inferred from the sequence in which the individual relations are selected and entered into the analogous structure. Participants usually chose the actor and recipient first (e.g., hunt: hunter → game), followed by the instrument (e.g., rifle), the location (e.g., forest) and, often at a comparatively late stage, the objective (e.g., to bag a deer). This sequence of concept selection points to the existence of saliency weightings in the components of the individual concepts. Moreover, these results confirm that a moderate degree of similarity is essential not only for felicitous metaphors, but for creative analogies. Our experiments have shown that particularly characteristic features or relations can have preferential status in both the recognition and construction of analogies (Klix and Bachmann 1992). The originality of an analogy is dependent on factors such as the age and intelligence of its constructor, and analogy completion tasks are often employed in intelligence tests such as the Raven ‘progressive matrices,’ Sternberg (1977) has linked the factor structure of human intelligence to the solution of analogy tests. Moreover, Gentner and Sternberg have constructed algorithms which realize analogy detection. All of these are based on the comparison of features or semantic relations (Greeno and Riley 1984).
9. Models Of Analogy Detection
Following the initial, very simple approaches to the processes of analogy detection, the dominant paradigm is now based on a model devised by Rips et al. (1973) which has been modified and extended by Bachmann (1998). According to this model, the following three aspects must be checked before an analogy can be accepted:
(a) Do the terms to be compared share a common feature which is much more salient than others? In train: railway and bus: truck; for example, the means of transport is so prominent that the analogy is immediately accepted.
(b) If this is not the case, the global impression is assessed. This entails a kind of compression of the available information, as discussed above in connection with Gluck and Bower’s experiments.
(c) If this global comparison does not result in a decision, the concepts are closely scanned for common features and relations (deliberate checking). If no acceptable similarities are found, the analogy is rejected.
Unfortunately, the question of how much processing time is required for each of these components is as yet unanswered.
10. The Role Of Analogy Construction In Scientific Innovation
The relationship between analogical reasoning and intelligence has been investigated in countless experiments and tests, with children and young adults of various ages, using plant, animal, object, and abstract analogies. However, there has been far less investigation of the ways in which analogy construction has impacted on the history of science, and the momentous mental achievements and creative insights which have resulted from this.
Many significant examples can be found to illustrate how analogical reasoning has helped to break new ground in the history of science. The origins of analogy-based scientific innovation can be traced back to the early stages of Greek thought, with Archimedes one of its most eminent representatives. The Egyptian shadoof—a long-armed water-raising device used to draw water from wells—was invented long before Archimedes’ time, and it was known that levers could be used to amplify physical force. It was left to Archimedes, however, to discover the relationship between the two arms, and thus to establish the principle of the lever. Hence mechanics—an essential precursor of physics—was founded on the basis of a number-pair analogy between the respective distances from the fulcrum and force relations according to the principle of levers. This development was founded on a paradigm of analogical thought, i.e., load arm: effort arm = length A: length B. Using the same method, i.e., in analogy to the principle of the lever, Archimedes was also able to calculate the surface area of any segment of a parabola (Serres 1994).
Eratosthenes is thought to be the first person to have calculated the earth’s circumference. People had known how to determine the circumference of a circle using 360 since Babylonian times (influenced by the Sumerian sexagesimal system). Eratosthenes applied this knowledge in the following analogy: The distance between Syene (now Aswan) and Alexandria was approximately 800 km (in today’s system of measurement). Once a year, the sun was at its zenith directly over a well in Syene and hence there are no shadows at that location at that time. At the same time in Alexandria, it cast a shadow from which it could be calculated that the sun was 7 from the zenith. This represents a difference of about 1 50 of a complete circle, hence the distance between Alexandria and Syene is about 1/50 of the earth’s circumference. By multiplying the distance (800 km) by 50, Eratosthenes calculated the earth’s circumference to be approximately 40,000 km.
In his famed Dialogue on the Two Chief World Systems (the Ptolemaic system and the Copernican system), Galileo contradicted the Aristotelians of the time. The Aristotelians advocated the Ptolemaic hypothesis, and presented the following argument against the Copernican model: Assuming that Copernicus is right in saying that the earth rotates around its own axis, the circumference of the earth is such that this must happen at high speed—40,000 km in 24 hours (or 920 m in some 2 seconds’ free fall). As a test of the Copernican system, one can climb a high tower, drop a stone from the top, and note the position at which it hits the ground. Since the earth is turning while the stone is falling, the stone should be noticeably removed from the foot of the tower when it makes contact with the earth. This is not the case, however. The stone falls perpendicular to the tower and hits the ground at its foot. According to the Aristotelians, this disproved the Copernican system. Using the character of Salviati in the Dialogue as his mouthpiece, Galileo refuted this argument with the following analogy: Imagine a sailing boat traveling at high speed. If a stone is dropped from the top of the mast, it will hit the deck at the foot of the mast, since it retains the speed of the boat until it hits the ground. Galileo thus invalidated the anti-Copernican argument by means of an analogy.
The most impressive known example of analogical reasoning in scientific discovery is provided by the equations describing electromagnetism derived by James Clerk Maxwell in 1864. Maxwell’s contemporary, Michael Faraday, had demonstrated the existence of electric and magnetic fields, showing that iron filings sprinkled on a thin piece of paper held above a magnet are attracted to its ‘lines or force’ or its poles. Maxwell investigated the properties of the lines of force described by Faraday and discovered similarities between the behavior of these lines of force and the flow of a liquid in a pipe. The equations for the latter were already known. Maxwell transferred this knowledge to magnetic fields and electric currents, and was thus able to define the behavior of magnetic lines of force at and between poles. Writing on this means of discovery, Maxwell postulated that in order to form an idea of physical laws for which no theory is available, it is necessary to familiarize oneself with the existence of physical analogies. The discovery of the interaction between electric currents and magnetic fields laid the foundations of the theory and practice of electromagnetism, and hence of the dynamo technology at the close of the nineteenth century. Moreover, it was the precursor of radio and television wave transmission, since one of Maxwell’s analogous equations had suggested that radio waves must also exist. Twenty years after Maxwell presented his basic equations, Heinrich Hertz indeed succeeded in producing radio waves under laboratory conditions— another demonstration of how creative thought in the form of analogical reasoning can impact dramatically on the history of science and the fate of humankind.
Bibliography:
- Bachmann T 1998 Die Ahnlichkeit zwischen analogen Wissensdomanen [The similarity between analogous domains of knowledge]. Doctoral dissertation, Humboldt University, Berlin
- Becker O 1990 Grundlagen der Mathematik in geschichtlicher Entwicklung [Foundation of mathematics in historical development]. STW, Freiburg, Germany
- Beyer R 1991 Untersuchungen zum Verstehen und zum
- Gestalten von Texten [Investigations of the comprehension and organisation of texts]. In: Klix F, Roth E, van der Meer E (eds.) Kognitive Prozesse und geistige Leistung. Deutscher Verlag der Wissenschaften, Berlin
- Bolzano B 1970 Wissenschaftslehre [Scientific model]. Akademie Verlag, Berlin
- Gentner D, Stevens A L 1983 Mental Models. Lawrence Erlbaum, Hillsdale, NJ
- Gluck M A, Bower G H 1988 From conditioning to category learning: An adaptive network model. Journal of Experimental Psychology: General 117: 227–47
- Greeno J G, Riley M S 1984 Prozesse des Verstehens und ihre Entwicklung [Processes of comprehension and their development]. In: Weinter F E, Kluwe R (eds.) Metakognition, Motivation und Lernen. Kohlhammer, Stuttgart, Germany, pp. 252–74
- Hoffmann J 1993 Vorhersage und Erkenntnis [Prediction and Knowledge]. Hogrefe, Gottingen, Germany
- Horgan G 1995 Die neuen Sozialdarwinisten [The new Social Darwinists]. Spektrum der Wissenschaft 12: 80–90
- Kahnemann D, Tversky J A 1973 On the psychology of prediction. Psychological Review 80: 207–51
- Klix F, Bachmann T 1992 Analogy detection—analogy construction: An approach to similarity in higher order reasoning. Zeitschrift fur Psychologie 206: 125–43
- Leibniz G W 1960 Fragmente der Logik [Fragments of Logic]. Akademie Verlag, Berlin
- Rips L J, Shoben E J, Smith E E 1973 Semantic distance and the verification of semantic relations. Journal of Verbal Learning and Verbal Behavior 12: 1–20
- Rumelhart D E 1979 Some problems with the notion of literal meanings. In: Ortony A (ed.) Metaphor and Thought. Cambridge University Press, Cambridge, UK
- Schmidt H-D 1966 Leistungschance, Erfolgserwartung und Entscheidung [Chance, Expectation and Decision]. Deutscher Verlag der Wissenschaften, Berlin
- Serres M 1994 Elemente einer Geschichte der Wissenschaften [Elements of a History of Science]. Suhrkamp, Frankfurt, Germany
- van der Meer E 1991 Die dynamische Struktur von Ereigniswissen [The dynamic structure of event-related knowledge]. In: Klix F, Roth E, van der Meer E (eds.) Kognitive Prozesse und geistige Leistung. Deutscher Verlag der Wissenschaften, Berlin
- Wason P C, Johnson-Laird P N 1972 Psychology and Reasoning. Harvard University Press, Cambridge, MA




