Motor Control Models Research Paper

With the advent of technical means for capturing motion sequences and the pioneering work of Marey and Muybridge in this area, the attempt at describing, modeling, and understanding the organization of movement has become a scientific topic. The fact that human movements are part of everyday life paradoxically hides their intrinsic complexity and justifies initial expectations that complete knowledge could be achieved simply by improving the measurement techniques and carrying out a few carefully designed experiments. Unfortunately, this is not the case. Each experiment is frequently the source of more questions than answers and thus the attempt to capture the complexity of purposive action and adaptive behavior, after a century of extensive multidisciplinary research, is far from over.

The conventional view is based on a separation of perception, movement, and cognition and the segregation of perceptual, motor, and cognitive processes in different parts of the brain, according to some kind of hierarchical organization. This view is rooted in the empirical findings of neurologists of the nineteenth century, such as J. Hughlings Jackson, and has a surprising degree of analogy with the basic structure of a modern PC that typically consists of input and output peripherals connected to a central processor. Perhaps the analogy with modern technology justifies why this old-fashioned attitude still has its supporters, in spite of the massive empirical and conceptual challenge to this view and its inability to explain the range of skills and adaptive behaviors that characterize biological organisms.

Let us consider perception, which is the process whereby sensory stimulation is translated into organized experience. That experience, or percept, is the joint product of the stimulation and of the process itself, particularly in the perception and representation of space. An early theory of space perception put forth by the Anglican bishop G. Berkeley at the beginning of the eighteenth century was that the third dimension (depth) cannot be directly perceived in a visual way since the retinal image of any object is twodimensional, as in a painting. He held that the ability to have visual experiences of depth is not inborn but can only result from logical deduction based on empirical learning through the use of other senses.

The first part of the reasoning (the need of a symbolic deductive system for compensating the fallacy of the senses) is clearly wrong and the roots of such misconception can be traced back to the neoplatonic ideas of the Italian Renaissance, in general, and to Alberti’s window metaphor, in particular. Also, the Cartesian dualism between body and mind is just another face of the same attitude and such Descartes’ error, to quote Damasio (1994), is on a par with the Berkeley’s error above and is at the basis of the intellectualistic effort to explain the computational complexity of perception which characterizes a great part of the classic artificial intelligence approach. However, the latter part of Berkeley’s conjecture (the emphasis on learning and intersensory integration) is surprisingly modern and agrees, on one hand, with the modern approach to neuropsychological development pioneered by Piaget and, on another, with the so-called connectionist point of view, originated in the 1980s as a computational alternative to classic artificial intelligence.

An emergent idea is also the motor theory of perception, well-illustrated by Berthoz (1997); that is, the concept that perception is not a passive mechanism for receiving and interpreting sensory data but is the active process of anticipating the sensory consequences of an action and thereby binding the sensory and motor patterns in a coherent framework. In computational terms, this implies the existence in the brain of some kind of ‘internal model,’ as a bridge between action and perception. As a matter of fact, the idea that the instructions generated by the brain for controlling a movement are utilized by the brain for interpreting the sensory consequences of the movement is already present in the pioneering work of Helmholtz and von Uexkull and its influence has resurfaced in the context of recent control models based on learning (e.g., Wolpert and Kawato 1998). The generally used term is ‘corollary discharge’ (von Holst and Mittelstaedt 1950) and implies an internal comparison between an outgoing signal (the efferent copy) and the corresponding sensory re-afference: the coherence of the two representations is the basis for the stability of our sensorimotor world. This kind of circularity and complementarity between sensory and motor patterns is obviously incompatible with the conventional reasoning based on hierarchical structures. A similar kind of circularity is also implicit in Piaget’s concept of ‘circular reaction,’ which is assumed to characterize the process of sensorimotor learning; that is, the construction of the internal maps between perceptually identified targets and the corresponding sequence of motor commands.

An additional type of circularity in the organism/environment interaction can be identified at the mechanical interface between the body and the outside world, where the mechanical properties of muscles interact with the physics of inanimate objects. This topic area has evolved from the Russian school, with the early work on the nature of reflexes by I. P. Pavlov and the subsequent critical re-examination by P. K. Anhokin and N. Bernstein. In particular, we owe to Bernstein the seminal observation (the comparator model ) that motor commands alone are insufficient to determine movement but only identify some factors in a complex equation where the world dynamics has a major influence. This led, among other things, to the identification of muscle stiffness as a relevant motor parameter and the formulation of the theory of equilibrium-point control (Feldman and Levin 1995, Bizzi et al. 1992).

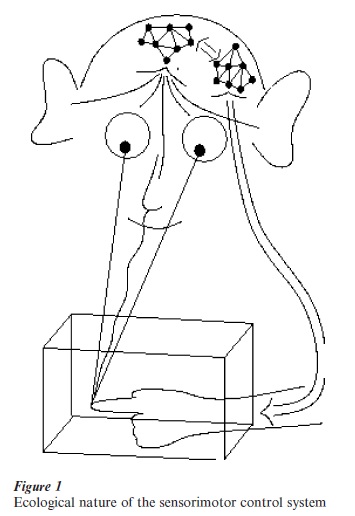
In general, we may say that, in different ways, Helmholtz’s corollary discharge, Piaget’s circular reaction, and Bernstein’s comparator model are different ways to express the ecological nature of motor control; that is, the partnership between brain processes (including muscles) and world dynamics. This concept is graphically sketched in Fig. 1. On the other hand, these general ideas on motor control could not provide, immediately, mathematical tools of analysis from which to build models and perform simulations. The art and science of building motor control models is a later development and has been influenced by the methods designed by engineers in the field of automatic control and computer science. Most of the techniques are based on linear approximations and explicit schematizations of the phenomena. In particular, two main concepts can be singled out for their influence on the study of motor control: the concept of feedback and the concept of motor program. Their level of influence in brain theory is certainly determined by the tremendous success of these techniques in the modern technological world. However, their applicability to what we may call the biological hardware is questionable for two main reasons: (a) Feedback control can only be effective and stable if the feedback delays are negligible, but this is not the case for biological feedback signals, where transduction and transmission delays add up to tens of milliseconds; (b) The concept of motor program implies a sequential organization, which only can be effective if the individual steps in the sequence are sufficiently fast, and this is in contrast with the parallel, distributed processing of the brain made necessary by the relative slowness of synaptic processing. In fact, the recognition of the limits of the analytic–symbolic approach has motivated, since the late 1980s, a re-evaluation of earlier approaches under the new light of connectionist thinking.

1. Trajectory Formation

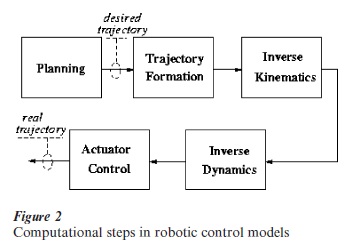
The computational process that is necessary for realizing a planned motor task has been the subject of a great deal of research in robotics. As sketched in Fig. 2, five main subproblems can be identified: (a) planning, (b) trajectory formation, (c) inverse kinematics, (d) inverse dynamics, and (e) actuator control. In the robotic approach, the blocks correspond to different procedures to be executed in a sequence. However, this is only an implementation strategy, quite natural for the usual engineering hardware, but probably inappropriate for the biological hardware. The first two processes correspond to the intuitive idea of imagining and then drawing a figure on a piece of paper. This implies selecting the initial point, the size and orientation of the figure, and then breaking down the complex trajectory of the pen that realizes such intention into a sequence of pen strokes, smoothly joined together in a quasi-continuous curve. However, for the pen to faithfully follow the intended path, the brain must first figure out the patterns of angular rotations of the different joints, the so-called inverse kinematic problem. This is a difficult computational task because the human arm (and the body in general) has a high degree of ‘kinematic redundancy,’ in the sense that there is an excess number of degrees of freedom and thus the same pen stroke can be realized by means of an infinite number of joint rotation patterns. The biological solution to this problem is characterized by an invariant spatiotemporal structure whose main feature is that the elementary strokes are approximately straight, with a symmetric bell-shaped speed profile (Morasso 1981), and whose global smoothness is well approximated by a criterion of ‘minimum jerk’ (Flash and Hogan 1985). In any case, the computations described above only cover the first three blocks of Fig. 2. The real challenge is in the inverse dynamics block and there are reasons to assume that the controllable compliant properties of muscles can relieve the brain of at least part of the computational burden, which must be explicitly shouldered by conventional robotic systems because torque motors have zero stiffness.

2. The Theory Of Equilibrium-Point Control

This theory is dependent on the elastic properties of muscles, that are well captured by the so called λ-model (Feldman and Levin 1995). In this model, λ is the controllable parameter that sets the activation threshold of the monosynaptic stretch reflex and thus determines the ‘rest length’ of the ‘muscle spring’ (Fig. 3). Its value is specified by supraspinal motor commands and expresses a combination of the desired levels of muscle length and stiffness. By setting the λ-commands of all the muscles, the brain implicitly codes an equilibrium point, determined by the fact that at this point the spring actions cancel each other. In this way, movement follows as a mechanical consequence of the force field, without a continuous intervention of the brain. In Fig. 3, the ‘Recruitment’ block corresponds to the exponential family of curves (shifted to the left according to the rack and pinion mechanism, operated by the λ-command); ‘Tetanic fusion’ refers to the relatively slow force build-up for sudden changes of motor commands; ‘Hill’s law’ is the nonlinear dependence of muscle’s force on the muscle’s speed of contraction. Moreover, the brain can take advantage of a second type of redundancy, the ‘muscle redundancy’: the excess number of muscles in relation to the number of degrees of freedom. The important feature is that muscles are not linear springs but are characterized by length–tension curves of exponential type, whose stiffness depends on the difference between the λ-command and the actual muscle length. Therefore, the brain has the opportunity of independently controlling two variables: (i) the global equilibrium point, by setting the λ-commands equal to the muscle lengths of a desired posture (the reciprocal λ-commands); (ii) the global stiffness of the joints, by adding to the previous pattern a set of coactivation λ-commands (the stronger the coactivation, the stronger the stiffness).

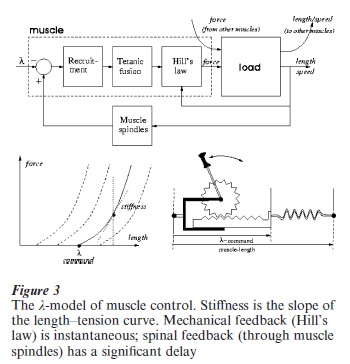
The implications of this model are extremely relevant but the interpretation of the experimental data is still controversial. There is no doubt that muscle stiffness can be seen as a kind of implicit feedback mechanism that tends to overcome the action of external and internal disturbances and loads, such as the action of gravity and the intrinsic dynamics of the body masses. The big question is concerned with the quantitative and functional relevance of this effect. For some researchers, muscle stiffness is all that is needed, without any kind of internal dynamic model. In this view, the brain is only supposed to generate equilibrium-point trajectories (the reciprocal commands) and to set up an appropriate level of coactivation. A very important feature of this model is that it assigns a computational role to the muscles, in addition to its obvious executive action. The defenders of this view also point out that an explicit feedback control action, supposedly mediated by proprioceptive signals and the corresponding reflex mechanisms, is ruled out by the large delays in the feedback loops, which are known to be of the order of tens of milliseconds and thus sufficient to cause a feedback control solution to be unstable. In spite of its elegance and appealing ‘ecological’ nature, this extreme form of equilibrium-point control model would only be plausible if the empirical values of muscle stiffness, at equilibrium as well as during movement, were strong enough in relation to the usual dynamics of body motion. The problem is that this is a difficult type of measurement and there is not yet a complete agreement on the available data; however, it is fair to say that, although stiffness is certainly relevant as a cofactor, its natural level is probably not enough to fully counteract the body dynamics, at least in more demanding dynamic tasks. For example, its role is likely to be much greater in the case of handwriting movements, which involve relatively small masses, than in the case of sway movements in upright standing, which are affected by the whole body mass.

3. Dynamic Compensation

The alternative solution is some combination of ‘feedforward’ and (explicit) ‘feedback’ control, in addition to the implicit feedback provided by muscle stiffness. In general, a feedforward control model is based on the anticipatory computation of the disturbances that will be encountered by a system when it attempts to carry out a desired plan of motion. This computation is complex and requires learning; a good example is given by the ‘feedback error learning’ model (Kawato and Gomi 1992) where the feedforward block is trained according to the residual errors of an underlying feedback controller. Figure 4 shows a modified version of the model that takes into account the intrinsic feedback due to the elastic muscle properties, ignored in Kawato’s original model. In the figure, the feedback error (the discrepancy between the desired and real trajectories) is used as the learning signal of the trainable feedforward model, which gradually takes over the responsibility of counterbalancing the dynamic disturbances, thus acquiring an internal model of body dynamics that generates an additional type of motor command: the dynamic compensation λ-command, to be added to the reciprocal and coacti ation commands defined above (Morasso and Sanguineti 1997).

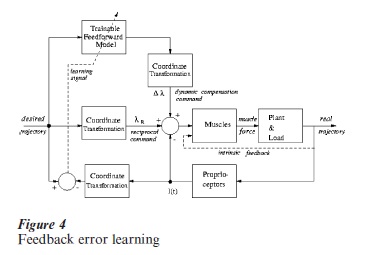
This example introduces the next big issue for understanding the trend in motor control modeling, the issue of motor learning, which has been deeply influenced by the advent in the early 1980s of connectionist theories and techniques.

4. Learning Paradigms In Neural Networks

At the core of the theories of neural network models is the attempt to capture general approaches for learning from experience tasks that are too complex to be expressed by means of explicit or symbolic models (Arbib 1995). The mechanism of learning and memory has been an intriguing question after the establishment of the neuron theory at the turn of the nineteenth century (Ramon y Cajal 1928) and the ensuing conjectures that memories are encoded at synaptic sites (Hebb 1949) as a consequence of a process of learning. In accordance with this prediction, synaptic plasticity was first discovered in the hippocampus and nowadays it is generally thought that LPT (long-term potentiation) is the basis of cognitive learning and memory, although the specific mechanisms are still a matter of investigation.

Three main paradigms for training the parameters or synaptic weights of neural network models have been identified: (a) ‘Supervised learning,’ in which a teacher or supervisor provides a detailed description of the desired response for any given stimulus and exploits the mismatch between the computed and the desired response or error signal for modifying the synaptic weights according to an iterative procedure. The mathematical technique typically used in this type of learning is known as back propagation and is based on a gradient–descent mechanism that attempts to minimize the average output error; (b) ‘Reinforcement learning,’ which also assumes the presence of a ‘supervisor’ or teacher but its intervention is only supposed to reward (or punish) the degree of success of a given control pattern, without any detailed input–output instruction. The underlying mathematical formulation is aimed at the maximization of the accumulated reward during the learning period; (c) ‘Unsupervised learning,’ in which there is no teacher or explicit instruction and the network is only supposed to capture the statistical structure of the input stimuli in order to build a consistent but concise internal representation of the input. The typical learning strategy is called ‘Hebbian,’ in recognition of the pioneering work of D. O. Hebb, and is based on a ‘competitive’ or ‘self-organizing’ mechanism that uses the local correlation in the activity of adjacent neurons and aims at the maximization of the mutual information between stimuli and internal patterns.

5. Adaptive Behavior And Motor Learning

The neural machinery for learning and producing adaptive behaviors in vertebrates is sketched in Fig. 5, which emphasizes the recurrent, nonhierarchical flow of information between the cerebral cortex, the basal ganglia/thalamus, and the cerebellum. A growing body of evidence has been accumulated in recent years that challenges the conventional view of segregated processing of perceptual, motor, and cognitive information (Shepherd 1998). For example, it was usually considered that basal ganglia and cerebellum were specialized for motor control and different cortical areas were devoted to specific functionalities, with a clear separation of sensory, motor, and cognitive areas.

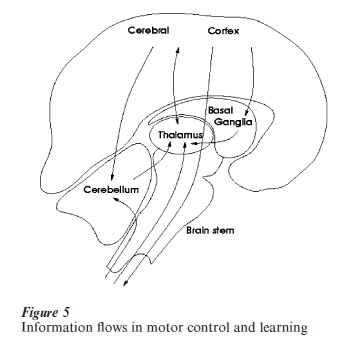
This is not now the conventional wisdom and the emerging picture is that the three main computational sites for adaptive behavior are all concerned with processing sensorimotor patterns in a cognitive– sensitive way but are specialized as regards the learning paradigms and the types of representation: (a) The cerebral cortex appears to be characterized by a process of unsupervised learning that affects its basic computational modules (the micro-columns that are known to have massive recurrent connections). The function of these computations might be the representation of non-linear manifolds, such as a body schema in the posterior parietal cortex (Morasso and Sanguineti 1997). This view seems to be contradicted by the ‘fractured shape’ of cortical maps (Rizzolatti et al. 1998), but the apparent contradiction may only be a side effect of the basic paradox faced by the cortical areas: how to fit higher dimensional manifolds (such as a proprioceptive body schema) on to a physically flat surface; (b) The cerebellum is plausibly specialized in the kind of supervised learning exemplified by the feedback error learning model. Moreover, the cerebellar hardware (characterized by a large number of microzones, comprising mossy-fiber input, bundles of parallel fibers, output Purkinje cells, with teaching signals via climbing fibers) is well designed for the representation of time series, according to a sequencein sequence-out type of operation (Braitenberg et al. 1997); (c) The basal ganglia are known to be involved in events of reinforcement learning that are required for the representation of goal-directed sequential behavior (Sutton and Barto 1998).

6. A Distributed Computational Architecture

Figure 6 summarizes many of the points outlined above and outlines in which direction we may expect future research to be directed. It must be emphasized that in spite of its apparent simplicity the sketched model is extremely complex from many points of view: (a) it is nonlinear; (b) it involves high-dimensional variables; (c) it has a coupled dynamics, with internal and external processes; (d) it is adaptive, with concurrent learning processes of different types. No simulation model of this complexity has been constructed so far, partly because the mathematical tools for its design are only partially available.

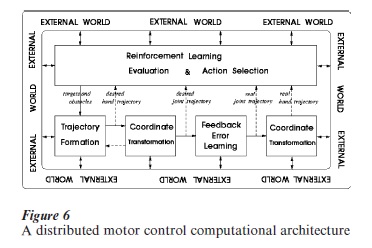
However, there is a need for improving our current level of understanding in this direction because this is the only sensible way for interpreting the exponentially growing mass of data coming from new measurement techniques, such as advanced brain imaging. As a matter of fact, since the time of Marey, better measurement techniques of movement analysis have required better and better models of motor control, and vice versa.

In the figure, the reader may recognize the presence of computational modules already considered: ‘trajectory formation’ and ‘feedback error learning.’ The latter, in particular, obviously is characterized by a supervised learning paradigm and thus we may think that its main element (the ‘trainable feedforward model’) is implemented in the cerebellar circuitry. The learning signal, in this case, is the discrepancy between the desired trajectory (the motor intention) and the actual trajectory, determined by the combined body– environment dynamics and measured by different proprioceptive channels. In a sense, the brain acts as its own supervisor, setting its detailed goal and measuring the corresponding performance: for this reason it is possible to speak of a self-supervised paradigm.

The underlying behavioral strategy is an active exploration of the ‘space of movements’ also known as ‘babbling,’ in which the brain attempts to carry out randomly selected movements that become the teachers of themselves.

On the other hand, the trajectory formation model cannot be analyzed in the same manner. It requires different maps for representing task-relevant variables, such as the position of the objects obstacles in the environment, the position of the body with respect to the environment, and the relative position of the body parts. Most of these variables are not directly detectable by means of specific sensory channels but require a complex process of ‘sensory fusion’ and ‘dimensionality reduction.’ This kind of processing is characteristic of associative cortical areas, such as the posterior parietal cortex which is supposed to hold maps of the body schema and the external world (Paillard 1993) as a result of the converging information from different sensory channels. The process of cortical map formation can be modeled by competitive Hebbian learning applied both to the thalamocortical and cortico-cortical connections: the former connections determine the receptive fields of the cortical units whereas the latter support the formation of a kind of high-dimensional grid that matches the dimensionality of the represented sensorimotor manifold. In a cortical map model, sensorimotor variables are represented by means of ‘population codes’ which change over time as a result of the map dynamics. For example, the ‘Trajectory formation’ module of Fig. 6 can be realized by means of a cortical map representation of the external space that can generate a time varying population code corresponding to the ‘desired hand trajectory.’ Another map can transform the ‘desired hand trajectory’ into the corresponding ‘desired joint trajectory,’ thus implementing a transformation of coordinates from the ‘hand space’ to the ‘joint space.’ This kind of distributed architecture is necessary for integrating multisensory redundant information into a task-relevant, lower-dimensional representation of sensorimotor spaces. On top of this computational layer, that operates in a continuous way, there is a layer of reinforcement learning that operates mostly by trial and error through two main operating modules: an ‘actor’ that selects a sequence of actions and a ‘critic’ that evaluates the reward and influences the action selection of the next trial. In the model of Fig. 6 it is the reinforcement learning module that decides the allocation of ‘targets and obstacles’ for the next trial.

Bibliography:

1. Anokhin P K 1974 Biology and Neurophysiology of Conditioned Reflexes and their Role in Adaptive Behaviour. Pergamon Press, Oxford, UK
2. Arbib M A 1995 The Handbook of Brain Theory and Neural Networks. MIT Press, Cambridge, MA
3. Bernstein N A 1957 The Coordination and Regulation of Movement. Pergamon Press, Oxford, UK
4. Berthoz A 1997 Le sens du mouvement. Edition Odile Jacob, Paris
5. Bizzi E, Hogan N, Mussa Ivaldi F A, Giszter S F 1992 Does the nervous system use equilibrium-point control to guide single and multiple movements? Behavioral and Brain Sciences 15: 603–13
6. Braitenberg V, Heck D, Sultan F 1997 The detection and generation of sequences as a key to cerebellar function: Experiments and theory. Behavioral and Brain Sciences 20: 229–45
7. Damasio A R 1994 Descartes’ Error. Emotion, Reason and the Human Brain. Putnam Press, New York
8. Feldman A G, Levin M F 1995 The origin and use of positional frames of references in motor control. Behavioral and Brain Sciences 18: 723–45
9. Flash T, Hogan N 1985 The coordination of arm movements: An experimentally confirmed mathematical model. Journal of Neuroscience 7: 1688–1703
10. Hebb D O 1949 The Organization of Behavior. Wiley, New York
11. von Holst E, Mittelstaedt H 1950 Das Reaff Wechselwirkungen zwischen Zentralnervensystem und Peripherie. Naturwissenschaften 37: 464–76
12. Jeannerod M 1988 The Neural and Behavioral Organisation of Goal-directed Arm Movements. Clarendon Press, Oxford, UK
13. Kawato M, Gomi H 1992 A computational model of four regions of the cerebellum based on feedback error learning. Biological Cybernetics 69: 95–103
14. Marey E J 1894 Le mouvement. Edition Masson, Paris
15. Morasso P 1981 Spatial control of arm movements. Experimental Brain Research 42: 223–7
16. Morasso P, Sanguineti V 1997 Self-organization, Cortical Maps and Motor Control. North Holland, Amsterdam
17. Muybridge E 1957 The Human Figure in Motion. Dover Press, New York
18. Paillard J 1993 Brain and Space. Oxford University Press, Oxford, UK
19. Piaget J 1963 The Origin of Intelligence in Children. Norton Press, New York
20. Ramon y Cajal S 1928 Regeneration in the Vertebrate Central Nervous System. Oxford University Press, Oxford, UK
21. Rizzolatti G, Luppino G, Matelli M 1998 The organization of the cortical motor system: New concepts. Electrencephalography and Clinical Neurophysiology. 106: 283–96
22. Shepherd G M 1998 The Synaptic Organization of the Brain. Oxford University Press, Oxford, UK
23. Sutton R S, Barto A G 1998 Reinforcement Learning. MIT Press, Cambridge, MA
24. Wolpert D M, Kawato M 1998 Internal models of the cerebellum. Trends in Cognitive Science 2: 338–47