Classical Decision Theory Research Paper

Because of this history the term ‘statistical decision theory’ can be understood as referring to an important group of specific theorems due to Wald and later extended and refined by others, as discussed below; or it can be understood in a much broader sense as a description of the frequentist outlook inherent in the work of Neyman, Pearson, and Wald, among others. This research paper focuses on the former point of view, which is undoubtedly the more widely held interpretation. For a discussion of the latter point of view see Brown (2000).

1. Key Elements

1.1 Basic Concepts

The key elements that set formal decision theory apart from the remainder of statistical theory are the notions of ‘loss’ and ‘risk’ and the consequent concepts of ‘admissibility’ and ‘minimaxity.’ Consider a statistical problem with a sample space, Ξ and a family of possible distributions, {F: FϵΦ}. These elements should be part of any carefully specified statistics problem. Often Φ is parametrized so that it can be written as Φ ={F_θ: θϵΘ}. Θ is then called the ‘parameter space,’ problems in which Φ cannot be nicely parametrized by a subset of Euclidean space are often referred to as nonparametric.

In addition, Decision Theory requires specification of a set of possible decisions or actions, ∆, to be taken after observation of the data. Possible types of decisions include estimates of the parameter, hypothesis tests related to subsets of parameters, confidence intervals, or predictions about potential future observations. A ‘loss function’ describes the loss—or negative advantage—of taking a particular action, dϵ∆, when FϵΦ is the true distribution. The resulting function can be written as L (F, d ), or as L (θ, d ) when the ‘states of nature’ in ∆ have been given a parametric representation. Usually, L≥0. A nonrandomized procedure is a map δ: Ξ→∆. (Randomized procedures can also be defined. They are useful for developing parts of the theory, even if they are almost never used in practice.) The ‘risk,’ R, is the expected loss of δ under F

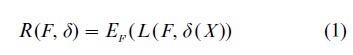
These basic notions lead naturally to a comparison of potential decision procedures that defines δ as ‘better than’ δ₂ if

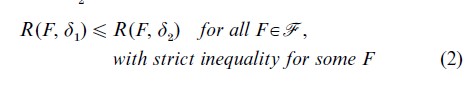
The admissible procedures are those that are minimal in the sense of this partial ordering; thus, δ is admissible if there is no other procedure that is better.

1.2 Example: Inference About A Binomial Proportion

Inference about a binomial proportion is an important problem, in terms of both basic theory and statistical practice. We only discuss here the most basic version of this problem. In this the statistician observes the value of a binomial variable reflecting an unknown proportion, p.

One common objective involves estimation of p. (In terms of the preceding formal definitions, Ξ ={0, 1, …, n} and ∆ ={d: 0≤d≤1} and Φ={ F_p:0 >p≤1} with F_p indicating the binomial distribution with sample size n and proportion p.) For this objective a conventional loss functi on is squared error loss, defined by L (p, d ) =(d -p)². See Sect. 3.2 for some further discussion of this example.

Another common objective involves testing a null hypothesis about p. The null hypothesis may be, for example, that p=p₀ for some fixed, pre-specified value p . Then the two possible decisions correspond to the statements ‘do not reject H₀’ and ‘reject H₀.’ The conventional loss function here ascribes loss 0 to a correct decision and 1 to an incorrect one. A related problem concerns the construction of confidence intervals for p. There is an intimate relation between this and the testing problem. See, for example, Lehmann (1986) or Robert (1994 Chap. 5).

1.3 Example: Estimation Of Normal Means

Another important paradigm in both theory and practice involves the estimation of one or more normal means. In the simplest version of this problem the statistician observes the sample mean, X of a normal sample. In variants of the problem the standard deviation of the population may either be known or unknown. The first variant is easier to treat mathematically but the second is more common in applications. If the objective is to estimate the unknown population mean, say, µ, then a conventional loss function is squared error loss given by L ( d, µ)=(d -µ)², for an estimate d being any real number. Testing and confidence interval problems are also of interest for such a family of distributions.

Many generalizations of this formulation are of practical importance, and their theory has been extensively researched. The most prominent situation includes the normal linear model. This setting includes such common statistical topics as the Analysis of Variance. In Sect. 3.1 of this research paper we discuss in more detail the situation that arises when one looks at several independent normal means simultaneously.

1.4 Discussion

For some authors, the law of large numbers interpretation of the expectation in (1) has suggested that the statistician contemplates a situation in which the identical experiment will be independently repeated an arbitrarily large number of times. Moreover, for the law of large numbers to apply one needs formally also that the same value of F appears in each of these repetitions. Such an interpretation has been on occasion criticized as impractical, and as invalidating the premises of decision theory. However this interpretation is not required as a logical basis for the theory. It was also apparently not contemplated in the work of Neyman and Pearson that motivated Wald’s development.

One can instead consider a collection of independent experiments, each having its own structure. A statistician who uses a collection of procedures many of which are inadmissible will not fare well in the long run by comparison to a statistician who uses a better procedure for each individual problem. One may find early reflections of this attitude in Clopper and Pearson (1934) or in Neyman and Pearson (1933). (It can be argued further that it would be still better to adopt a coherent collection of admissible procedures in such a situation. See for example, Savage (1972 [1954]), who proposes subjective Bayesian methods as the means toward this end.)

Typically, in applications much care is given to realistic specification of the family of distributions in this formulation. When this cannot be done with satisfactory precision then robust methods are often recommended. Such methods can be placed directly within the above framework by considering a suitably large set for Φ. Huber (1981) has a careful treatment of this nature and proposes an often-used robust procedure with important decision theoretic properties.

The action space, ∆, is also generally subject to careful and realistic specification. The loss function, on the other hand, is not so often specified with the same degree of precision and attention to the practical situation at hand. It is common to adopt certain conventional loss functions, most prominently squared error or normalized squared error in real valued estimation problems or squared Euclidean distance in vector valued ones. In hypothesis testing problems a zero-one loss is similarly conventional and predominantly used. It has sometimes been argued that statisticians should expend more care on realistic specification of the loss or on a robust treatment of families of losses. See Robert (1994, Sect. 2.6) for more discussion of this issue.

2. Classical Themes

2.1 Characterization Theorems

A major objective of classical decision theory is to characterize the admissible procedures, or special subsets of them, in a mathematically tractable fashion. Many of these characterizations involve the notion of a Bayes procedure. Corresponding to any ‘prior’ probability measure, G, on the parameter space a Bayes procedure can be defined either as a procedure that minimizes the average risk with respect to G or, equivalently, as one that minimizes the conditional risk given the observation, for almost every possible observation.

A basic result in Wald’s work, later developed further by others, is that a Bayes procedure is automatically admissible if it is essentially uniquely determined. It is also admissible under mild additional conditions guaranteeing continuity of risks if the prior is supported on the entire parameter set. Wald also proved a fundamental converse result: if the parameter space is finite then every admissible procedure is Bayes. He, and others, also extended this result to classes of settings where the parameter space is bounded. See Robert (1994, Sect. 6.3) for a general discussion of such results.

Here, as elsewhere, Wald acknowledged his debt to earlier work on hypothesis testing by noting that these facts about Bayes procedures could provide an alternate interpretation and an alternate proof for the Neyman–Pearson Lemma, and for various generalizations to multiple classification problems. As Wald also frequently noted, these estimators are Bayes only in a formal mathematical sense in that the decision theoretic motivation for their use is frequentist in nature (via the risk function) rather than fundamentally Bayesian (via the conditional expected loss given the data).

If the parameter space is not compact then one cannot expect that all admissible procedures will be Bayes for some prior. However there are a variety of characterizations in such settings of admissible procedures as types of limits of Bayes procedures. In some cases—usually involving exponential families—these characterizations can be extended to prove that all (or most) admissible procedures can be represented as generalized Bayes procedures. That is to say, they can be represented as formally calculated posterior conditional expectations with respect to non-negative measures that are not necessarily finite.

In some special problems more can be proven. The most notable case is the problem of estimating under squared error loss the mean of a multivariate normal distribution having known covariance matrix. There it is also possible to give an explicit characterization of the generalized priors that correspond to admissible procedures. Such a result relies in part on a method for proving admissibility due to Blyth and developed further by Stein. Lehmann and Casella (1998, Chap. 5) discuss many of these results and provide additional references.

2.2 Minimaxity

Minimaxity is another fundamental decision theoretic property defined and treated in Wald’s seminal work. A procedure δ* is minimax if

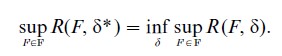
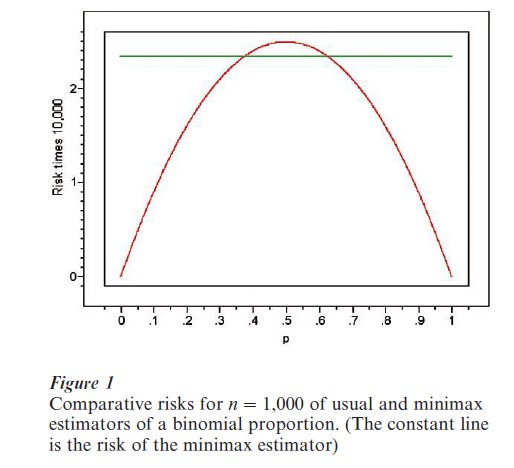
Examination of this formal definition shows that minimaxity is a very cautious, conservative criterion. A minimax procedure is the one that does best if the true F Φ turns out to be the worst possible from the statistician’s perspective. In some special problems the minimax procedure provides a broadly satisfactory choice for a decision rule. In others it turns out that minimax rules are not admissible, or are not satisfactory because other rules have more appealing risk functions. A simple classical example may make clear how this can happen. Consider the binomial estimation problem described in Sect. 2.2. The ‘usual’ estimate of p is the sample proportion p =X/n. It can be shown that this is not minimax under squared error loss. Instead, the minimax estimator has the somewhat more complicated formula p*=( X+√n/2)/(n+√n). The respective risks of these estimators can be plotted. See Fig. 1, which plots these risks for the moderately large value, n=1,000. Examination of these plots makes clear that p would generally be preferable to p* in this setting, since its risk is usually smaller and often much smaller. (The exceptions would be situations where the statistician was nearly convinced that p was quite near 0.5.)

Even in cases where the minimax procedure itself may not be satisfactory, comparison with the minimax risk can provide a useful starting point for judging the worth of proposed procedures. The essays in Brown (1994) and Strawderman (2000) comment on the role of minimaxity as a benchmark for evaluating and developing alternate procedures.

2.3 Sequential Decision Theory

At the same time as he was developing statistical decision theory, Wald was also building a theory of sequential decision procedures. Wald (1947), his monograph on the topic, appeared three years before his monograph on statistical decision functions. It can be argued that there is nothing intrinsically decision theoretic in the idea of sequential stopping that is the basis for this theory. However the structure that Wald created was so thoroughly imbued with the spirit of decision theory that it has since usually been viewed as a part of it. Sequential procedures allow the experimenter to conduct the experiment in stages with a decision to stop the experiment or to continue made after each stage. In a decision theoretic version the size of the stopped sample is included as part of the overall loss function.

The most dramatic result of Wald’s research here is the optimal property of the Sequential Probability Ratio Test (SPRT) in Wald and Wolfowitz (1948). The proof of this optimality property relies on a representation of the SPRT as a Bayes procedure, and uses much of the decision theoretic machinery else-where developed by Wald. The most prominent modern embodiment of this sequential idea undoubtedly lies in the area of sequential clinical trials. Here the spirit of Wald’s work remains as an important foundation, even if the subject has mostly gone in more numerical and pragmatic directions. See Siegmund (1994) for a contemporary overview of sequential decision theory and Jennison and Turnbull (1999) for a recent comprehensive treatment of clinical trials.

2.4 Hypothesis Testing

The basic theory of hypothesis testing was largely developed by Fisher and by Neyman and Pearson in the decades before Wald began his codification of decision theory. It can be argued that Fisher’s view of testing was not fundamentally decision theoretic. Fisher’s formulation requires a specification of the distributions in the null hypothesis and of a test statistic, but it does not require specification of the possible distributions in the alternative. Neyman and Pearson proceeded further to require these to be specified, and this enabled them to study the com-peting requirements of high power under the alternative and low power under the distributions in the null hypothesis. (This power should be bounded by the significance level, α.) The Neyman–Pearson theory is clearly decision theoretic and, as noted above, can be cast exactly into the mold created by Wald. Sub-sequent work of Lehmann, Stein and others has more fully developed the theory. Lehmann (1986) contains a definitive high-level treatment of the theory and selected applications.

2.5 Invariance

Statistical invariance is the embodiment of an intuitive demand. The invariance principle applies when the decision theoretic elements of the problem are invariant under the action of a group of one-to-one transformations. (Some authors use the term ‘equivariant’ for parts of this specification.) In that case the principle demands that the decision procedure adopted also be invariant (or equivariant) under the action of this group. Although the principle seems reason-able, and the resulting procedures often have intuitive appeal, it turns out that they need not be admissible. See below for a brief discussion of the Stein phenomenon, a situation where appealing invariant procedures are inadmissible.

There are structural conditions on the group that can guarantee that there do exist invariant procedures that are minimax. The first such theorem of this type is contained in an unpublished manuscript by Hunt and Stein. In the ideal case where there is a best invariant procedure these conditions then guarantee that this best invariant procedure is minimax. See Kiefer (1957) and Brown (1986a) for more information about invariance and the Hunt–Stein theorem.

2.6 Asymptotics

The basic concepts and tools of decision theory have also been carried into the domain of asymptotic statistical theory. Le Cam was the leader in this activity by formulating and developing such concepts as asymptotic sufficiency, contiguity, local asymptotic normality, and local asymptotic minimaxity. In Le Cam (1953) the seminal paper beginning his development, he included a careful treatment of the concept of asymptotic superefficiency, and a proof in parametric problems that it was limited to sets of Lebesgue measure zero. See Le Cam and Yang (2000) for a presentation of many of these topics, and for further references.

3. Contemporary Developments

3.1 Bayesian Decision Theory

Stein (1956) described the inadmissibility of the usual estimator of a three or more dimensional multivariate normal mean. This initially surprising discovery spur-red activity in decision theory, changed many statistical attitudes and preconceptions, and continues to influence current statistical methodology. For estimating the vector of means from a multivariate normal sample under squared-error loss the usual procedure, X, is intuitive and has various nice theoretical properties, such as those of being best invariant and minimax. It is also the formal Bayes procedure corresponding to the uniform, Lebesgue measure as the formal prior. Note that Lebesgue measure is also Jeffreys prior for this problem, and hence corresponds to a standard ‘noninformative’ Bayesian prescription. See Jeffreys (1939) or Robert (1994, Sect. 3.4). This usual estimator is surprisingly not admissible when there are three or more normal means involved.

James and Stein (1961) intensified Stein’s earlier discovery by describing an estimator that dominates the usual one by a significant amount. Brown (1971) later demonstrated that all admissible procedures in this problem are either Bayes or formal Bayes, and also characterized which of these priors leads to admissible estimators. Strawderman (1971) subsequently used a hierarchical Bayes construction to derive formal Bayes estimators for this problem that are both minimax and admissible. When the dimension is at least 5 then some of these are actually proper Bayes. Efron and Morris (1973) explained how Stein’s estimator could be derived via an empirical Bayes approach. A combined effect of these developments is to demonstrate the importance of a careful choice of prior or formal prior for such multivariate problems and to provide some guidelines for the form of such priors. Ensuing research has led in the directions of empirical Bayes methods, of robust Bayes methods, and also of methods involving careful specification of hierarchical priors. The influence of Stein’s decision-theoretic discovery on contemporary Bayesian analysis is discussed at length in such monographs as Berger (1985) and Robert (1994, especially Chaps. 6 and 8).

3.2 Unbiased Estimates Of Risk

Stein’s discovery has also led to other methodological and substantive advances in decision theory. The most important of these undoubtedly revolve around Stein’s (1981) unbiased estimate of the risk. For generalizations and other related results see Brown (1986b, Chap. 4). Where it applies, as it does in the preceding multivariate normal problem, the unbiased estimate of the risk provides a powerful tool for finding procedures that dominate previous proposals and for suggesting new, satisfactory estimates.

3.3 Nonparametric Function Estimation

Much current research in nonparametric function estimation involves a synthesis of several aspects of statistical decision theory, including asymptotic decision theory, minimax theory, and results and methods related to the James–Stein phenomenon described above. A typical problem involves the observation of a nonparametric regression. Suppose for example that {x_i:i=1, …, n} is a given subset of predictors, e.g., x_i=i/n, and Y_i ≈N(m(x_i), σ²) are independent normal variables with mean m ( x_i). The goal is to estimate the unknown function , m, under a loss function such as ∑_i(m (x_i)-m( x_i))². The problem is nonparametric in that minimal assumptions are made about the form of m. For example, one might assume only that these functions are in a given ball in a Sobolev space or a Besov space. Using a variation of Le Cam’s asymptotic decision theory various papers have recently shown that several apparently distinct problems of this character are actually asymptotically isomorphic in a decision-theoretic sense. Consult Johnstone (2000) for references.

As a sort of culmination of much research in this area, Donoho et al. (1990) proved a minimax theorem for linear estimators in such a problem. These results, and later extensions, relate the minimax risk under a restriction to linear procedures to the usual, unrestricted minimax risk for the problem. In turn, this result can be used to describe the asymptotic behavior of the unrestricted minimax value. One consequence is a determination of the minimax asymptotic rate of convergence for the risk of estimators in this problem. Imbedded in the proofs is also a practical methodology, essentially due to earlier work of Ibragimov and Hasminskii, for deriving the minimax linear procedure.

3.4 Adaptive Estimation

A new variation of the minimax concept has come forward here in order to try to overcome the inherently conservative and global nature of minimaxity. This is the notion of adaptive minimaxity. Adaptive mini-maxity is defined relative to a collection, X, of subsets of the possible distributions, Φ. A procedure is adaptively minimax to within a factor K if

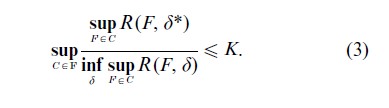
Procedures built from wavelet bases have been shown by Donoho, Johnstone and others to possess desirable asymptotic adaptive minimax properties. It should also be noted that both James–Stein estimation and Stein’s unbiased estimate of risk play a key role here, and in further refinements in this area. Johnstone (2000) discusses many of these issues and provides additional references. Donoho and Johnstone have also developed a new form of decision-theoretic tool, the ‘oracle inequality,’ that has been instrumental in papers written in the early twenty-first century such as these.

Bibliography:

1. Berger J O 1985 Statistical Decision Theory and Bayesian Analysis, 2nd edn. Springer, NY
2. Brown L D 1971 Admissible estimators, recurrent diffusions and insoluble boundary value problems. Annals of Mathematical Statistics 42: 855–903 (Correction 1973 Annals of Statistics 1: 594–96
3. Brown L D 1986a Commentary on paper [19]. J. C. Kiefer Collected Papers, Supplementary Volume. Springer, New York, pp. 20–27
4. Brown L D 1986b Fundamentals of Statistical Exponential Families. Institute of Mathematical Statistics. Hayward, CA
5. Brown L D 1994 Minimaxity, more or less. In: Gupta S S, Berger J O (eds.) Statistical Decision Theory and Related Topics. V. Springer, New York, pp. 1–18
6. Brown L D 2000 An essay on statistical decision theory. Journal of the American Statistical Association 95: 1277–81
7. Clopper C J, Pearson E S 1934 The use of confidence or fiducial limits illustrated in the case of the binomial. Biometrika 26: 404–13
8. Donoho D L, Liu R C, MacGibbon B 1990 Minimax risk over. hyperrectangles, and implications. Ann. Statist. 18: 1416–37
9. Efron B, Morris C 1973 Stein’s estimation rule and its competitors—an empirical Bayes approach. Journal of the American Statistical Association 68: 117–30 Huber P J 1981 Robust Statistics. Wiley, New York
10. James W, Stein C 1961 Estimation with quadratic loss. Proc. Fourth Berk. Symp. Math. Statist., and Prob. 1: 311–19
11. Jeffreys H 1948,1961 [1939] The Theory of Probability. Oxford University Press, Oxford, UK
12. Jennison C, Turnbull B W 1999 Group Sequential Methods with Applications to Clinical Trials. Chapman and Hall, Boca Raton, FL
13. Johnstone I M 2000 Function estimation in Gaussian noise: Sequence models. http://www-stat.stanford.edu/imj
14. Kiefer J 1957 Invariance, minimax sequential estimation, and continuous time processes. Annals of Mathematical Statistics 28: 573–601
15. Le Cam L 1953 On some asymptotic properties of maximum likelihood estimates and related Bayes estimates. University of California Publications in Statistics 1: 277–330
16. Le Cam L, Yang G L 2000 Asymptotics in Statistics: Some Basic Concepts, 2nd edn. Springer, New York
17. Lehmann E L 1986 Testing Statistical Hypotheses, 2nd edn. Springer, New York
18. Lehmann E L, Casella G 1998 Theory of Point Estimation. Springer, New York
19. Neyman J, Pearson E S 1933 The testing of statistical hypotheses in relation to probabilities a priori. Proceedings of the Cambridge Philosophical Society 29: 492–510
20. Robert C P 1994 The Bayesian Choice: A Decision Theoretic Motivation. Springer, New York
21. Savage L J 1972 [1954] The Foundations of Statistics. Dover Publications, New York
22. Siegmund D 1994 Sequential Analysis. Springer, New York
23. Stein C 1956 Inadmissibility of the usual estimator for the mean of a multivariate normal distribution. Proceedings of the Third Berkeley Symposium on Mathematical Statistics and Probability 1: 187–95
24. Stein C 1981 Estimation of the mean of a multivariate normal distribution. Annals of Statistics 9: 1135–51
25. Strawderman W E 1971 Proper Bayes minimax estimators of the multivariate normal mean. Annals of Mathematical Statistics 42: 385–88
26. Strawderman W E 2000 Minimaxity. Journal of the American Statistical Association 1364–8
27. Wald A 1939 Contributions to the theory of estimation and testing hypotheses. Annals of Mathematical Statistics 10: 299–326
28. Wald A 1947 Sequential Analysis. Wiley, New York
29. Wald A 1950 Statistical Decision Functions. Wiley, New York
30. Wald A, Wolfowitz J 1948 Optimal character of the sequential probability ratio test. Annals of Mathematical Statistics 19: 326–39