Bruno De Finetti Research Paper

He first became interested in probability as a result of reading an article in a popular magazine concerning Mendel’s laws of genetics, which stimulated him to write an article of his own on the subject. His article attracted the attention of Corrado Gini and eventually led to a position as head of the Mathematical Office of the Instituto Centrale di Statistica. Later he accepted a position as actuary in the Assicurazioni Generali insurance company in Trieste, where he was concerned with automation of all actuarial, statistical, and bookkeeping operations and calculations. He became a lecturer in mathematics, actuarial mathematics, and probability at the Universities of Trieste and Padova, and later full professor in Trieste and finally at the University of Rome, from which he retired in 1976.

In 1957 he spent a quarter at the University of Chicago at the invitation of Professor Leonard Jimmie Savage (1917–71). They became friends and each stimulated the other in the development of his ideas. Although there are differences in the presentations of subjective probability by de Finetti and Savage, their basic outlook was the same, and they stood in sharp contrast to other figures in the field, with the exception of Frank Ramsey (1903–30), whose important article Truth and Probability (1926) was very much in the same spirit. De Finetti and Savage were the major figures of the twentieth century in the area of subjective probability, and legitimate heirs of the two giants, Emile Borel (1871–1956) and Henri Poincare (1854– 1912), who also viewed probability theory as a serious subject with numerous important real-world applications, rather than as a mathematical exercise. Both de Finetti and Savage were infuriated by the trivializations of the subject as such an exercise, which dominated the field during most of their lifetimes.

Early in his career de Finetti realized that there was something seriously lacking in the way probability and statistics were being developed and taught. The famous remark ‘Everybody speaks about Probability, but no one is able to explain clearly to others what meaning probability has according to his own conception,’ by the mathematician Garrett Birkhoff (1940), was indicative of serious problems even with the definition of probability. De Finetti found many of the standard assertions confused and meaningless. In his University of Rome farewell address (1977), concerning the contrast between himself and Savage (a mathematician who had been trained in the standard non-Bayesian theory) he said: ‘I, of course, was in quite the opposite situation: a layman or barbarian who had the impression that the others were talking nonsense but who virtually does not know where to begin as he cannot imagine the meaning that others are trying to give to the absurdities that it is imposing as dogma.’

De Finetti then attempted to formulate an appropriate meaning for a probability statement. His knowledge of philosophy and logic as well as mathematics, both pure and applied, enabled him to do so. The areas of his work that will be discussed here are his theory of exchangeability, theory of coherency, and theory of finitely additive probability. For him theory and practice were inseparable, and he emphasized the operational meaning of abstract theory, and particularly its role in making probabilistic predictions.

De Finetti rejected the concept of an objective meaning to probability and was convinced that probability evaluations are purely subjective. In his article Probability and my Life published in Gani (1982) he wrote: ‘The only approach which, as I have always maintained and have confirmed by experience and comparison, leads to the removal of such ambiguities, is that of probability considered—always and exclusively—in its natural meaning of ‘‘degree of belief.’’ This is precisely the notion held by every uncontaminated ‘‘man in the street.’’ De Finetti then developed a theory of subjective probability, corresponding to its use as an expression of belief or opinion, and for which the primary feature is coherency.

The starting point for his theory is the collection of gambles that one takes on, whether knowingly or unknowingly. These can be either ordinary gambles or conditional gambles, which are called-off if the contingency being conditioned upon does not occur. The simplest type of gamble is one on an event E, in which one receives a monetary stake S if E occurs and nothing otherwise. If a person values such a gamble at the sure amount p×S, then p is defined to be the probability of E for that person. In this evaluation one uses small stakes S so as to avoid utility complications, which distort probabilities evaluated in this way. One can then take linear combinations of such simple gambles to generate gambles in which there are a finite number of possible outcomes. Similarly, a called-off gamble on the event E given F, is such that one receives a monetary stake S if both events occur, nothing if F occurs but not E, and the gamble is called off if F does not occur. The value of such a conditional gamble for a person is called his or her conditional probability for E given F and is denoted by P(E|F).

In the work of de Finetti (1970, 1972, 1974–5) a primary aim is to avoid the possibility of a Dutch book, that is, to avoid sure loss on a finite collection of gambles. Thus suppose one has taken on a finite collection of gambles of any type whatsoever, including such things as investments, insurance, and so on. De Finetti proved that a necessary and sufficient condition for the avoidance of sure loss of a positive amount greater than some ε 0 on a finite number of unconditional gambles, consists in consistency with the axioms of finitely additive probability theory. These axioms are the usual ones, apart from the fact that the condition of finite additivity replaces that of countable additivity in the third axiom. Let P(E) denote the numerical probability for the event E. Then the axioms are:

1. P(W )=1, where W is the sure event.
2. For any event E, 0≤P(E)≤1.
3. The probability of a finite union of disjoint events

is the sum of the probabilities.

Further, if conditional gambles are also included, then to avoid a Dutch book, conditional probabilities must be evaluated in accord with the usual definition:

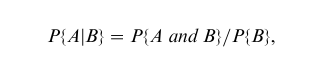
provided that P{B}>0. See Hill (1998) for further discussion.

In the subjectivistic conception a probability is essentially a price that one will pay for a certain gamble, with the understanding that this price can and will differ from one person to another, even apart from utility considerations. This conception is very close to that of the common person who speaks of probabilities for various real-world events based upon his or her own experience and judgment. In this case there is no need to confine attention to trials such as arise in games of chance. On the other hand, it is extremely interesting to see what the subjectivist interpretation of such trials might be. By considering this question, de Finetti developed his celebrated exchangeability theorem.

The problem that de Finetti posed and largely solved was that of justifying from a subjective point of view the importance of statistical frequencies in the evaluation of probabilities. Suppose that we have a sequence of events, E_i, for i=1,…, N, each of which may or may not occur, for example where E_i is the result of the ith flip of a coin. For convenience, we can assign the value 1 to heads and 0 to tails. It is natural sometimes to view the order of the flips as irrelevant, so that any permutation of the same sequence of outcomes is given the same probability. This leads to the notion of exchangeability, which is a symmetry condition, specifying that joint distributions of the observable random quantities are invariant under permutations. De Finetti proved a representation theorem which implies that if one regards a sufficiently long sequence of successes and failures as exchange- able, then it necessarily follows that one’s opinions can be represented, approximately, by a mixture of Bernoulli sequences, that is, of sequences for which there is a ‘true’ (but typically unknown) probability P of success, and such that conditional upon P=p, the observations are independent with probability p of success on each toss. The proportion of successes, as the number of trials goes to ∞, converges almost surely to P, and the initial or a priori distribution for P is also called the de Finetti measure for the process.

This representation in terms of Bernoulli sequences is exact for infinite sequences, and a slight modification holds also for finite sequences, the difference amounting to that between sampling with and without replacement from an urn. It also follows mathematically that provided a sufficiently long sequence has been observed, to a good approximation one will be led to base opinions about a future trial on the past empirical frequency with which the event has occurred, and this constitutes de Finetti’s justification for induction. In his work de Finetti emphasized prediction of observable quantities, rather than what is usually called inference about parameters. In other words, he was primarily interested in the posterior distribution of future observable random variables, rather than in the posterior distribution for the parameter P. This point of view has become known as predictivism in modern Bayesian statistics.

The exchangeability theorem of de Finetti allows one to analyze the relationship between subjective probabilities and the frequency theory of probability that developed from the work of Jakob Bernoulli. The fundamental stochastic process is known as a Bernoulli sequence. Such a sequence is by assumption such that on each trial there is a fixed objective probability p for success (1) and 1 p for failure (0), whose value may or may not be known, with the trials independent in the probabilistic sense. It is then a mathematical fact, known as the law of large numbers, that as the number of trials grows large the proportion of successes will stabilize at the ‘true’ probability p in the sense that the proportion of successes will converge almost surely to p; that is, the sequence converges except for a collection of outcomes that has probability 0.

Critics of this theory, such as de Finetti, argue that there are no real-world applications in which either p or the limiting proportion of successes is known to exist. The empirical support for the objectivist theory is merely that there are certain processes, such as coin flipping, dice throwing, card playing, draws from an urn with replacement, and so on, for which in finite sequences of trials the empirical proportions of successes appear to be in conformity with what the objectivist theory suggests. For example, if there are two similar balls in an urn, one red and one white, and if draws are made with replacement after substantial shaking of the urn, then experience suggests that the proportion of red balls in n draws, when n is sufficiently large, is around .5. Of course it is impossible to perform an infinite number of trials, so the limiting proportion, if it exists at all, can never be known. But in finitely many trials not only does the proportion of red balls drawn often seem to settle down to something like .5, but in addition, if say the n trials are repeated I times, then the proportion of these I trials in which there are exactly j red balls in n trials appears also to settle down to ( * j )(1/2⁰), more or less as the theory suggests. One must, however, exclude situations where such settling down does not appear to happen, and these are usually interpreted as meaning that the shaking was not adequate, or the cards not sufficiently well shuffled, and so on. Nonetheless, it appears that when sufficient care is taken, then the proportions appear to be roughly in accord with the objectivistic theory.

Does this imply that there exists a true p which is the objective probability, for example, that the ball drawn is red, and hence also that the proportion of red balls drawn must converge almost surely to .5? No one knows to this day. However, de Finetti’s exchange-ability theorem provides an alternative way to describe our experiences with such random events. A probability as before is merely a price that one would pay for a certain gamble. Under the assumption of an equal number of red and white balls, and that the urn is well shaken, symmetry suggests a price of .5 for the gamble in which you receive a dollar if a red ball is drawn, nothing otherwise. Similarly, if you were to be offered a gamble in which you would receive the dollar if the first two draws were red, then again symmetry together with the assumption that the urn is well shaken, suggest that a fair price would be .25. Continuing in this way we see that your prices are in accord with the usual probability evaluations for such an urn.

It is then a logical consequence of the exchange-ability theorem of de Finetti, that you must evaluate your probability that the sample proportion of red balls converges to .5 as unity. Note that this requires no circular definitions or mysterious conventions. There are, however, two important caveats. First, it is necessary that utility considerations be ignored, which necessitates that the prizes are not too large, and for this reason the stake S was taken to be one dollar. Alternatively, utility can be dealt with after the fashion of Ramsey or Savage. Second, the cases where people take this evaluation most seriously are those in which there have already been many draws in the past, indicating no cheating or violation of the apparent symmetry, so that in effect your probabilities are posterior probabilities based upon Bayes’ theorem. In other words: just as dice may be loaded so can other games be fixed, and a prudent bettor would not make the above evaluations merely from apparent physical and time symmetry alone, but rather in addition from experience that the game is not rigged and that the perception of symmetry is not mistaken. At any rate, one sees that it is not necessary to introduce the concept of an objective probability, but merely the experience that suggests an evaluation of .5.

The case of a Bernoulli sequence, whether interpreted according to the objectivist or subjectivist theory, is of course a very special example of an exchangeable sequence of random variables. For a Bernoulli sequence with p=.5, that is, a degenerate a priori distribution for P concentrated at the value .5, the primary difference between the two theories is that the objectivist theory objectifies the .5 which in the subjectivist theory is merely the opinion of the bettor, and similarly the .25 for drawing two red balls, and so on. In circumstances where prudent bettors have learned from experience to bet in accord with symmetry, the objectivist school states that the .5 and the .25 and so on, are the objective or true probabilities, not merely the values that the bettor chooses. Thus the objectivist theory implies that the proportion of successes necessarily converges to .5, while the subjective theory implies that the bettor must believe, with probability 1, that such convergence takes place.

It should be noted that countable additivity, that is, the modification of the third axiom to include also denumerable unions of disjoint events (which corresponds to a denumerable number of gambles) has never been demonstrated within the rigorous ap-proaches to probability theory and, as argued by de Finetti, is merely a particular continuity condition that one may or may not wish to adopt in a particular context, just as with the use of continuous functions in physics. The relaxation of the condition of countable additivity to finite additivity allows one greater freedom in the representation of degrees of belief. For example, the use of adherent mass distributions (which were introduced by de Finetti and are closely related to Dirac functions) allows one to obtain solutions for Bayesian non-parametric inference and prediction. See Hill (1993).

The work of de Finetti played a major role in the resurrection of the classical Bayesian approach to probability, statistics, and decision theory, as founded by Bayes and Laplace and developed by Gauss, Poincare, and Borel. His work continued the theory of induction of the British empiricists such as David Hume, and provided mathematically sound foundations for the modern-day subjective Bayesian approach.

Bibliography:

1. Birkhoff C 1940 Lattice Theory. American Mathematical Society Publication no. 25
2. De Finetti B 1970 Teoria delle probabilita. Einaudi, Turin, Italy
3. De Finetti B 1972 Probability, Induction and Statistics. Wiley, London
4. De Finetti B 1974–5 Theory of Probability, Vols. 1 and 2. Wiley, London
5. De Finetti B 1977 Probability: beware of falsifications. In: Aykac A, Brumat C (eds.) New De elopments in the Applications of Bayesian Methods. North-Holland, Amsterdam, pp. 347–79
6. Gani J (ed.) 1982 The Making of Statisticians. Springer-Verlag, New York
7. Hill B M 1993 Parametric models for An: Splitting processes and mixtures. Journal of the Royal Statistical Society, Series B 55: 423–33
8. Hill B M 1998 Conditional Probability. Encyclopedia of Statistics. Wiley, New York
9. Kolmogorov A 1950 Foundations of the Theory of Probability. English translation. Chelsea Press, New York