Social Network Models Research Paper

1. Statistical Models For Social Networks

1.1 Notation

In most of the literature on statistical models for networks, the set N = {1, 2,…, n} of network nodes is regarded as fixed and the edges, or ties, between nodes are assumed to be random. The tie linking node i to node j (i, j ϵ N) may be denoted by the random variable X_ij. In the simplest case of binary-valued random variables, X_ij takes the value 1 if the tie is present and 0 otherwise. Other cases of interest include:

(a) valued networks where X_ij is assumed to take values in the set {0, 1,…, C – 1};

(b) multiple relational or multivariate networks, where the variable X_ijk represents the possible tie of type k from node i to node j (with k ϵ R = {1, 2,…, r}, a fixed set of types of tie); and

(c) time-dependent networks, where X_ijt represents the tie from node i to node j at time t.

In each case, network ties may be directed (e.g., X_ij and X_ji are distinct random variables) or nondirected (e.g., X_ij and X_ji are not distinguished). The n n array X = [X_ij] of random variables can be regarded as the adjacency matrix of a random (directed) graph on N; the state space of all possible realizations of these arrays may be denoted by Ω_n. The array x = [x_ij] denotes a realization of X, with x_ij = 1 if there is an observed tie from node i to node j, and x_ij = 0 otherwise. In some cases, models may also refer to variables measured on actor attributes: for instance, the mth attribute Z_i^[m] of actor i gives rise to a random vector Z ^[m] with realization z^[m].

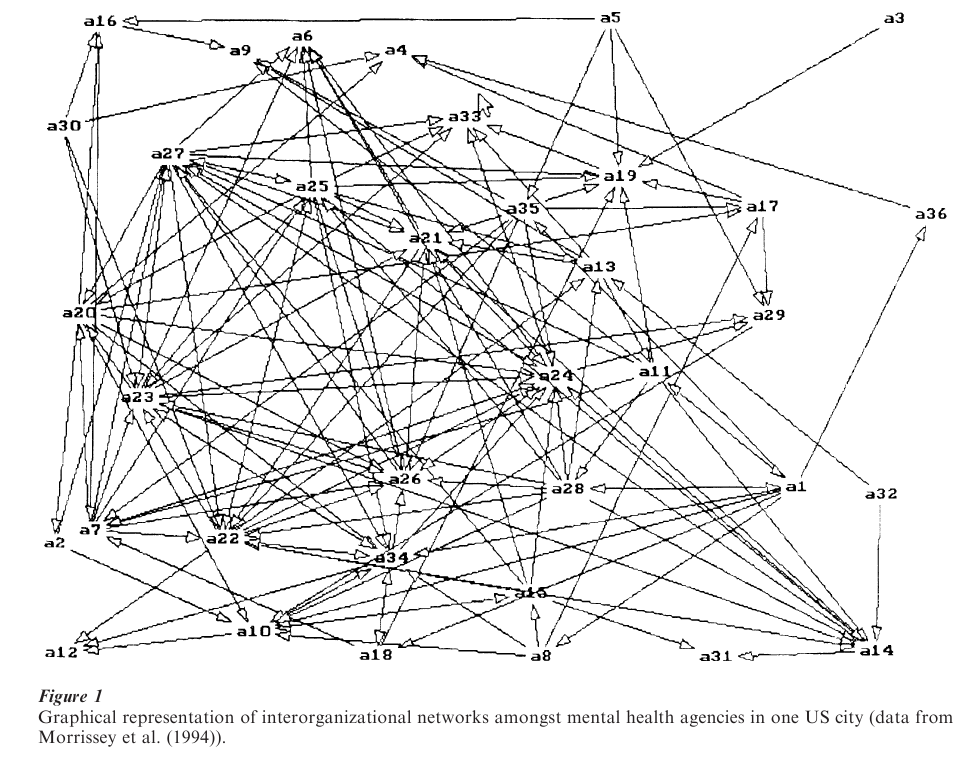
The adjacency matrix of an illustrative nondirected binary network is shown in Table 1. The data are from a study of interorganizational networks amongst mental health agencies conducted by Morrisey et al. (1994). The nodes of the network are 37 mental health agencies in one of the US cities in the Morrissey study; an edge links two agencies if they engage in regular and mutual exchange of information. The graphical representation of these data is shown in Fig. 1. We use this network to illustrate several of the distributions and models described below.

1.2 Bernoulli Graphs

A simple statistical model for a (directed) graph assumes a Bernoulli distribution, in which each edge,

or tie, is statistically independent of all others and governed by a theoretical probability P_ij. In addition to edge independence, simplified versions also assume equal probabilities across ties; other versions allow the probabilities to depend on structural parameters (Frank and Nowicki 1993). These distributions have often been used as models (Bollobas 1985), but are of questionable utility due to the independence assumption. Bernoulli graph distributions are described at length by Erdos and Renyi (1960) and Frank (1981).

1.3 Dyadic Structure In Networks

Statistical models for social network phenomena have been developed from their edge-independent beginnings in a number of major ways. In one important series of developments, the p model introduced by Holland and Leinhardt (1981), and developed by Fienberg and Wasserman (1981), recognized the theoretical and empirical importance of dyadic structure in social networks, that is, of the interdependence of the variables X_ij and X_ji. This class of Bernoulli dyad distributions and their generalization to valued, multivariate, and time-dependent forms, gave parametric expression to ideas of reciprocity and exchange in dyads and their development over time. The model assumes that each dyad (X_ij, X_ji) is independent of every other and, in a commonly constrained form, specifies:

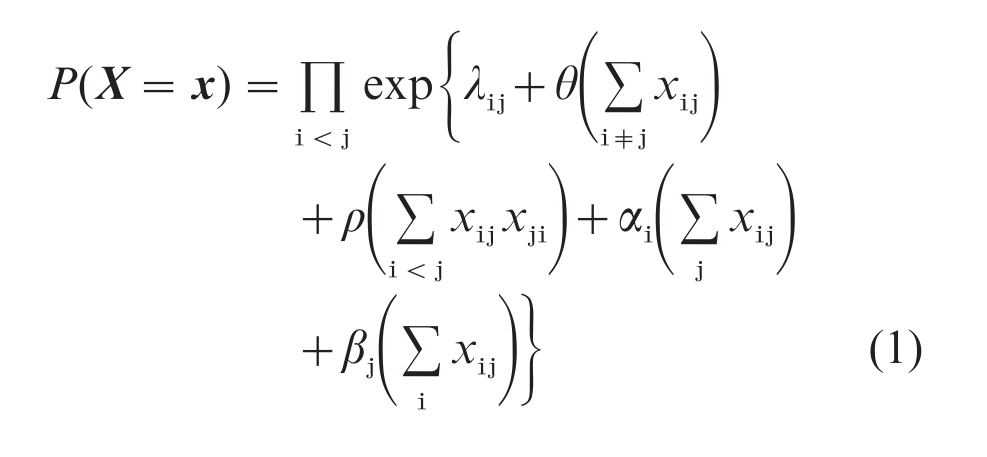
where θ is a density parameter; ρ is a reciprocity parameter; the parameters α_i and β reflect individual differences in expansiveness and popularity; and λ_ij ensures that probabilities for each dyad sum to 1. This model is log-linear.

An important elaboration of the p model permits the dependence of density, popularity and expansiveness parameters on a partition of the nodes into subsets that can either be specified a priori (e.g., from hypotheses about social position) or can be identified a posteriori from observed patterns of node interrelationships (e.g., Wasserman and Faust 1994). The resulting stochastic blockmodels represent hypotheses about the interdependence of social positions and the patterning of network ties (as originally elaborated in the notion of blockmodel by White et al. 1976). A potentially valuable variant of these models regards the allocation of nodes to blocks as a latent classification; Snijders and Nowicki (1997) have provided Bayesian estimation methods for the case of two latent classes. Another valuable extension of the p₁ model is the so-called p₂ model (Lazega and van Duijn 1997). Like the p₁ model, the p₂ model assumes dyad independence, but it adds the possibility of arbitrary node and dyad covariates for the parameters of the p₁ model, and models the unexplained parts of the popularity and expansiveness parameters as random rather than fixed effects.

1.4 Null Models For Networks

Despite the useful parameterization of dyadic effects associated with the p model and its generalizations, the assumption of dyadic independence has attracted sustained criticism. Thus, another series of developments has been motivated by the problem of assessing the degree and nature of departures from simple structural assumptions like dyadic independence. Following a general approach exemplified by early work of Rapoport (e.g., Rapoport 1949), a number of conditional uniform random graph distributions were introduced as null models for exploring the structural features of social networks (see Wasserman and Faust 1994 for a historical account). These distributions, denoted by U|Q, are defined over subsets Q of the state space Ω_n of directed graphs, and assign equal probability to each member of Q. The subset Q is usually chosen to have some specified set of properties (e.g., a fixed number of mutual, asymmetric, and null dyads, as in the U|MAN distribution of Holland and Leinhardt 1975). When Q is equal to Ω_n the distribution is referred to as the uniform (di)graph distribution, and is equivalent to a Bernoulli distribution with homogeneous tie probabilities. Enumeration of the members of Q and simulation of U|Q is often straightforward (e.g., see Wasserman and Pattison, in press), although certain cases, such as the distribution that is conditional on the indegree (∑x_ij) and outdegreee (∑_ij) of each node i in the net- work, require more complicated approaches (Snijders 1991, Wasserman 1977).

A typical application of these distributions is to assess whether the occurrence of certain higher-order (e.g., triadic) features in an observed network is unusual, given the assumption that the data arose from a uniform distribution that is conditional on plausible lower-order (e.g., dyadic) features (e.g., Holland and Leinhardt 1975). For example, the network displayed in Table 1 has 84 edges, and 333 and 69 triads with exactly 2 and 3 edges, respectively. If Q denotes the subset of complete Ω with 84 edges, the expected number of triads of each kind is 250.1 and 50.8, and the observed values lie at the 0.003 and 0.005 percentiles of the u|x₊₊ = 84 distribution, respectively. This general approach has also been developed for the analysis of multivariate social networks. The best- known example of this approach is probably the quadratic assignment procedure or model (QAP) for networks (Hubert and Baker 1978). In this case, the association between two graphs defined on the same set of nodes is assessed using a uniform multivariate graph distribution that is conditional on the unlabelled graph structure of each univariate graph. In a more general framework for the evaluation of structural properties in multivariate graphs, Pattison et al. (in press) also introduced various multigraph distributions associated with stochastic blockmodel hypotheses.

1.5 Extra-Dyadic Local Structure In Networks

A significant step in the development of parametric statistical models for social networks was taken by Frank and Strauss (1986) with the introduction of the class of Markov random graphs. This class of models permitted the parameterization of extra-dyadic local structural forms and so allowed a more explicit link between some important network conceptualizations and statistical network models. Frank and Strauss (1986) adapted research originally developed for modeling spatial dependencies among observations to graphs. They observed that the Hammersley-Clifford the oremprovidesa general probability distribution for X from a specification of which pairs (X_ij, X_kl) of edge random variables are conditionally dependent, given the values of all other random variables.

Define a dependence graph D with node set N(D) = {(X_ij: i, j ϵ N, i ≠ j} and edge set E(D) = {(X_ij, X_kl): X_ij and X_kl are assumed to be conditionally dependent, given the rest of X}. Frank and Strauss used D to obtain a model for Pr(X = x), denoted p* by Wasserman and Pattison (1996), in terms of parameters and substructures corresponding to cliques of D. The model has the form

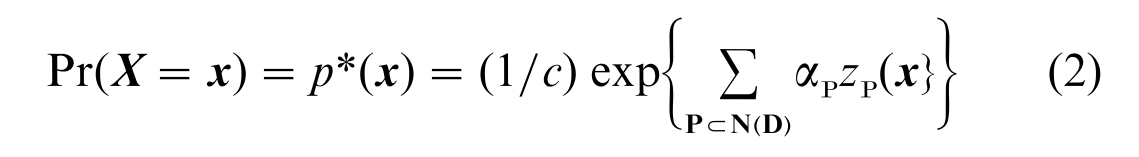
where:

(a) the summation is over all cliques P of D (with a clique of D defined as a nonempty subset P of N(D) such that |P| = 1 or (X_ij, X_kl) ϵ E (D) for all X_ij, X_kl ϵ P);

(b) z_p(x) = x_iΠ_j x_ij is the (observed) network statistic corresponding to the clique ρ of D; and

(c) c = Σ_x exp {Σ_pα_pz_p(x) is a normalizing quantity.

specification of a dependence graph raises a deep theoretical issue for network analysis: what constitutes an appropriate set of dependence assumptions? Frank and Strauss (1986) proposed a Markov assumption, in which (X_ij, X_kl) ϵ E(D) whenever {i, j} ∩ {k, l} ≠ φ. This assumption implies that the occurrence of a network tie from one node to another is conditionally dependent on the presence or absence of other ties in a local neighborhood of the tie. A Markovian local neighborhood for X_ij comprises all possible ties involving i and/or j. Any network tie is seen both as dependent on its neighboring ties and as participating in the neighborhood of other ties, so the resulting model embodies the assumption that social networks have a local self-organizing quality. In the case of Markovian neighborhoods, cliques in the dependence graph correspond to triadic and star-like network configurations. A homogeneity assumption, that model parameters do not depend on the specific identities of nodes but only on the network configurations to which they correspond, yields a model that expresses the probability of the network in terms of propensities for subgraphs of triadic and star-like structures to occur.

For example, a homogeneous Markov model for the network of Table 1 with parameters corresponding to edges, 2-stars, and triangles appears to be a substantial improvement in fit over a Bernoulli model with just an edge parameter, since the mean absolute residual for fitted edge probabilities drops from .220 to .175. Pseudolikelihood estimates for model parameters (Wasserman and Pattison 1996) are –3.31, 0.056, and 0.616 for edges, 2-stars, and triangles, respectively, suggesting that graphs with a large number of triangles are relatively more likely in the assumed homogeneous Markov p* distribution than those with few.

p* random graph models permit the parameterization of many important ideas about local structure in univariate social networks, including transitivity, local clustering, degree variability, and centralization. Valued (Robins et al. 1999) and multivariate (Pattison and Wasserman 1999) generalizations also lead to parameterizations of substantively interesting multi- relational concepts, such as those associated with balance and clusterability, generalized transitivity and exchange, and the strength of weak ties.

1.6 Prospects For Structural Models

The p* family of random graph models poses many interesting questions, both substantive and statistical. A major empirical question is the sufficiency of these local structural descriptions: do they suffice, or do they need to accommodate other characterizations of local dependence, more global considerations, other types of constraints (e.g., temporal and spatial), or variability in local structural dependencies? On the statistical side, major questions are raised by the complexity and rich parameterization of models that are deemed to be theoretically plausible. For instance, does a Markov chain Monte Carlo maximum likelihood approach to parameter estimation offer a viable alternative to approximate methods such as pseudolikelihood estimation (Strauss and Ikeda 1990)? How can these distributions best be simulated, and what are the convergence properties of various approaches, such as the Metropolis-Hastings algorithm?

2. Dynamic Models

Empirically and theoretically defensible parametric models for networks constitute one challenge for statistical modeling, but an arguably more significant challenge is to develop models for the emergence of network phenomena, including the evolution of networks and the unfolding of individual actions (e.g., voting, attitude change, decision-making) and interpersonal transactions (e.g., patterns of communication or interpersonal exchange) in the context of longer standing relational ties. Early attempts to model the evolution of networks in either discrete or continuous time assumed dyad independence and Markov processes in time.

A step towards continuous time Markov chain models for network evolution that relaxes the assumption of dyad independence has been taken by Snijders (1996). These models incorporate both random change and change arising from individuals’ attempts to optimize features of their local network environment (such as the extent to which reciprocity and balance prevail) and use the computer package SIENA for fitting. A tension function is proposed to represent the function that actors wish to minimize and Robbins-Munro procedures are used to estimate free parameters. The approach illustrates the potentially valuable role of simulation techniques for models that make empirically plausible assumptions; clearly, such methods provide a promising focus for future development.

The value of simulation has also been demonstrated by Watts and Strogatz (1998) and Watts (1999) in their analysis of the so-called small-world phenomenon (the tendency for individuals to be linked by short acquaintanceship network paths). They considered a probabilistic model for network change in which the probability of a new tie was determined, in part, by existing patterns of neighboring ties (a clustering component) and, in part, by a small random component. They used simulations to establish that only a small random component was needed for the simulated network to be likely to possess the small-world property.

3. Models Bridging Analytic Levels

A recurring theme among social theorists is the need for models that integrate the dynamic, interdependent, interpersonal, and cultural contexts in which social action occurs. The network modeling challenge posed by such framing of the nature of social processes is the development of models that represent interdependencies across several analytic categories (e.g., individuals, relational ties, settings, groups).

Snijder’s (1996) model for network change represents one step in this direction; the class of social influence models represents another (Friedkin 1998). These models are exemplified by the network effect model for the mth attribute variable:

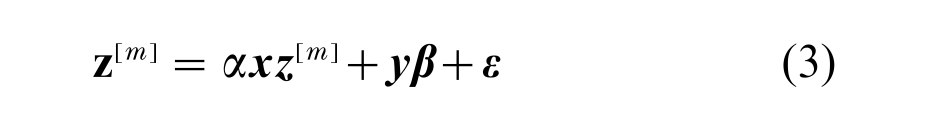
where α is a network effects parameter, y is a matrix of exogenous attribute variables with corresponding parameter vector β, and ε is a vector of residuals.

A further step in the direction of modeling interdependent node attributes and network ties has been to generalize the dependence graph approach to p* network models (Sect. 1.5) so as to include both node attribute variables (Z ^[m]) and relational variables (X ). This step is facilitated if directed dependencies are permitted in the dependence graph (i.e., dependencies in which one random variable is assumed to be conditionally dependent on a second, but the second not on the first). Robins et al. (in press) drew on graphical modeling techniques to construct models with directed dependencies among network ties and individual attributes. If the dependencies are directed from network ties to node attributes, models for social influence are obtained; with dependencies oriented from node attributes to network ties, social selection models result. Indeed, this generalization introduces substantial flexibility in model construction, with potential applications to joint influence and selection models, discrete time models for network change, network path models, and group-level attribute models.

The dependence approach of Sect. 1.5 has also been used to construct principled models for more general multiway relational data structures representing interdependent analytic categories. Examples to date have included bipartite (Faust and Skvoretz 1999) and k-partite (Pattison et al. 1998) graphs and illustrate how this general distribution has the capacity for a systematic and coherent approach to a variety of major network modeling challenges.

4. Conclusion

In addition to some of the specific future prospects already noted, a more general expectation is that the current classes of models are likely to be the foundation of substantial empirical and model-building activity in the early twenty-first century. From their early beginnings, statistical approaches to network modeling have now reached a point where sustained interaction is likely to be empirical research that allows the development of greatly improved models for processes occurring on networks, with important applications in many fields of social and behavioral science, including epidemiology, organizational studies, social psychology, and politics.

For more information on these approaches to social networks analysis, please see Wasserman and Faust (1994) and Wasserman and Pattison (1996, in press).

Bibliography:

1. Bollobas B 1985 Random Graphs. Academic Press, London
2. Erdos P, Renyi A 1960 On the evolution of random graphs. Publications of the Mathematical Institute of the Hungarian Academy of Sciences 5: 17–61
3. Faust K, Skvoretz J 1999 Logit models for affiliation networks. In: Becker M, Sobel M (eds.) Sociological Methodology 1999. Blackwell, New York, pp. 253–80
4. Fienberg S, Wasserman S 1981 Categorical data analysis of single sociometric relations. In: Leinhardt S (ed.) Sociological
5. Methodology 1981. Jossey-Bass, San Francisco, pp. 156–92
6. Frank O 1981 A survey of statistical methods for graph analysis. In: Leinhardt S (ed.) Sociological Methodology 1981. JosseyBass, San Francisco, pp. 110–55
7. Frank O, Nowicki K 1993 Exploratory statistical analysis of networks. In: Gimbel J, Kennedy J W, Quintas L V (eds.) Quo Vadis Graph Theory? A Source Book for Challenges and Directions. North-Holland, Amsterdam
8. Frank O, Strauss D 1986 Markov graphs. Journal of the American Statistical Association 81: 832–42
9. Friedkin N 1998 A Structural Theory of Social Influence. Cambridge University Press, New York
10. Holland P W, Leinhardt S 1975 The statistical analysis of local structure in social networks. In: Heise D R (ed.) Sociological
11. Methodology 1976. Jossey-Bass, San Francisco, pp. 1–45
12. Holland P W, Leinhardt S 1981 An exponential family of probability distributions for directed graphs. Journal of the American Statistical Association 76: 33–50
13. Hubert L J, Baker F B 1978 Evaluating the conformity of sociometric measurements. Psychometrika 43: 31–41
14. Lazega E, van Duijn M 1997 Position in formal structure, personal characteristics and choices of advisors in a law firm: A logistic regression model for dyadic network data. Social Networks 19: 375–97
15. Morrisey J P, Calloway M 1994 Local mental health authorities and service system change: Evidence from the Robert Wood Johnson Foundation Program on chronic mental illness. The Milbank Quarterly 72(1): 49–80
16. Pattison P, Mische A, Robins G L 1998 The plurality of social relations: k-partite representations of interdependent social forms. Keynote address, Conference on Ordinal and Symbolic Data Analysis, Amherst, MA, Sept. 28–30
17. Pattison P E, Wasserman S 1999 Logit models and logistic regressions for social networks, II. Multivariate relations. British Journal of Mathematical and Statistical Psychology 52: 169–194
18. Pattison P, Wasserman S, Robins G L, Kanfer A M 2000 Statistical evaluation of algebraic constraints for social networks. Journal of Mathematical Psychology 44: 536–68
19. Rapoport A 1949 Outline of a probabilistic approach to animal sociology, I. Bulletin of Mathematical Biophysics 11: 183–196
20. Robins G L, Pattison P, Elliott P 2001 Network models for social influence processes. Psychometrika 66: 161–190
21. Robins G L, Pattison P, Wasserman S 1999 Logit models and logistic regressions for social networks, III. Valued relations. Psychometrika 64: 371–94
22. Snijders T A B 1991 Enumeration and simulation methods for 0–1 matrices with given marginals. Psychometrika 56: 397–417
23. Snijders T A B 1996 Stochastic actor-oriented models for network change. Journal of Mathematical Sociology 21: 149–72
24. Snijders T A B, Nowicki K 1997 Estimation and prediction for stochastic blockmodels for graphs with latent block structure. Journal of Classification 14: 75–100
25. Strauss D, Ikeda M 1990 Pseudolikelihood estimation for social networks. Journal of the American Statistical Association 85: 204–12
26. Wasserman S 1977 Random directed graph distributions and the triad census in social networks. Journal of Mathematical Sociology 5: 61–86
27. Wasserman S, Faust K 1994 Social Network Analysis: Methods and Application. Cambridge University Press, New York
28. Wasserman S, Pattison P E 1996 Logit models and logistic regressions for social networks, I. An introduction to Markov random graphs and p*. Psychometrika 60: 401–25
29. Wasserman S, Pattison P E in press Multivariate Random Graph Distributions. Springer Lecture Note Series in Statistics, Springer-Verlag, New York
30. Watts D 1999 Networks, dynamics, and the small-world phenomenon. American Journal of Sociology 105: 493–527
31. Watts D, Strogatz S 1998 Collective dynamics of ‘small-world’ networks. Nature 393: 440–2
32. White H C, Boorman S, Breigen R L 1976 Social structure from multiple networks, I. Blockmodels of roles and positions. American Journal of Sociology 81: 730–80