Pattern Matching Research Paper

1. The Concept Of Pattern Matching

Pattern matching is a ubiquitous feature of knowledge processes in everyday life and in science. The use of pattern matching in everyday knowing, however, is different from pattern matching in mathematics, philosophy, and the social and behavioral sciences.

1.1 Rules Of Correspondence

Rules of correspondence are prescriptions that enable the mapping of one set of objects on another. Objects in a domain, D, are related to objects in a range, R, according to a rule of correspondence such as: Given a set of n countries in domain D, if the object in D is a one-party system, assign the number ‘0’ from range R. If it is a multiparty system, assign a ‘1.’ Rules of correspondence perform the same matching function as truth tables in symbolic logic, pattern recognition algorithms in computer science, and the use of modus operandi (M.O.) methods in criminology. When a single rule of correspondence is taken to define fully and unequivocally the properties of an event or object—for example, when responses to scale items on an intelligence test are taken to define ‘intelligence’—pattern matching becomes a form of definitional operationism (Campbell 1969, 1988, pp. 31–2).

1.2 The Correspondence Theory Of Truth

Until the late 1950s, philosophy of science was dominated by the correspondence theory of truth. The correspondence theory, the core epistemological doctrine logical positivism (see Ayer 1936), asserts that propositions are true if and only if they correspond with facts. The correspondence theory also requires that factually true propositions are logically validated against formal rules of logic such as modus ponens (p ͻ q, p, q ) and modus tollens (p ͻ q, ~ q, ~ p). To be verified, however, propositions must match facts (reality, nature). The correspondence version of pattern matching assumes a strict separation between two kinds of propositions—analytic and synthetic, logical and empirical, theoretical and observational—a separation that was abandoned after Quine (1951) and others showed that the two kinds of propositions are interdependent. Because observations are theory dependent, there is no theory-neutral observational language. Theories do not and cannot simply correspond to the ‘facts.’

1.3 Coherence Theories Of Truth

The correspondence theory has been replaced by a more complex form of pattern matching, the coherence theory of truth, which has a number of versions (see Alcoff 1996). In one version, often called the consensus theory of truth, beliefs are matched against other beliefs, with no requirement that they are tested empirically. Another version, realist coherentism (Putnam 1981), requires that two or more empirically tested beliefs are matched. William Whewell’s consilience theory of induction is closely related to this (qualified) realist version of the coherence theory. A third version of coherence theory is methodological pragmatism (Rescher 1980). Here, beliefs must satisfy cognitive requirements including completeness, consonance, consistency, and functional efficacy, all designed to achieve optimally plausible knowledge claims. Other versions of coherence theory require the additional condition that the social circumstances under which empirically tested beliefs arise be taken into account. These other versions include ‘social epistemology’ (Fuller 1991) and the ‘sociology of scientific validity’ (Campbell 1994).

1.4 Statistical Estimation And Curve Fitting

Statistical principles, rules, or criteria are applied to achieve an optimal match between a curve and a set of data points or observations. An example is the least squares criterion (the squared distance between observed and predicted values is a minimum or least value), where the match between the pattern supplied by a (linear or nonlinear) curve and a pattern of observations is approximate and probable, not certain as in pattern matching by rules of correspondence. The degree to which a curve and a set of observations match is summarized by coefficients of different kinds. Some of these represent the goodness-of-fit between curve and observations, while others represent the magnitude of error in pattern matching. Although coefficients are assessed according to a probability distribution, and given a p-value, the same observations can fit different curves; and the same curve can fit different observations. In such cases, pattern matching is as much a matter of plausible belief as statistical probability.

1.5 Context Mapping

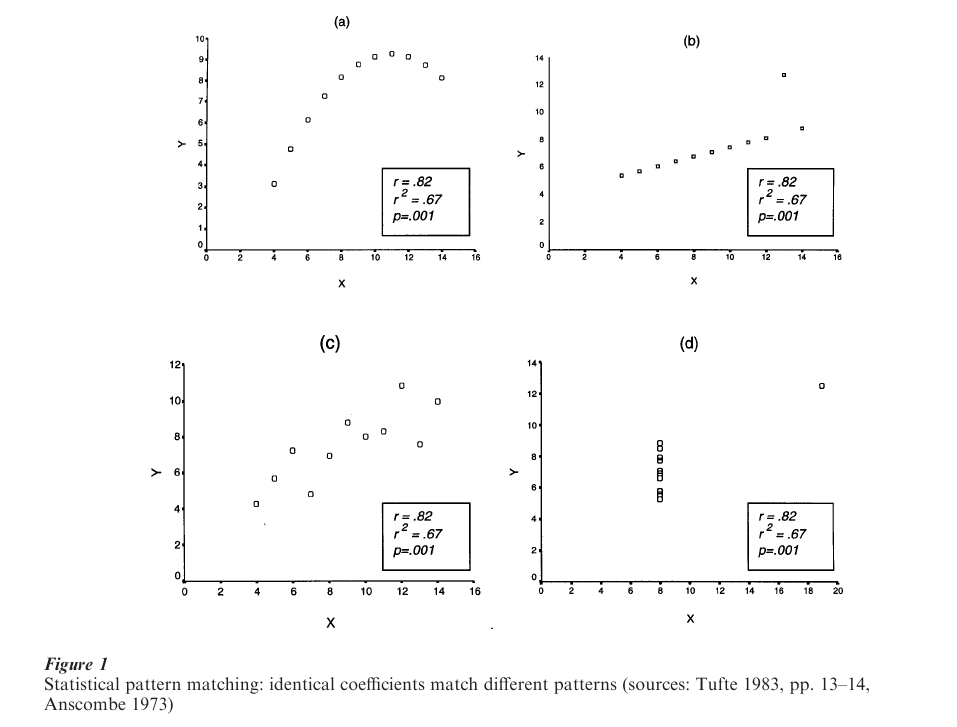
Closely related to curve fitting is context mapping. Knowledge of contexts is essential for understanding elements within them. Context mapping, which is epitomized by the figure-ground relation in Gestalt psychology, also applies to the analysis and interpretation of statistical data. For example, observations in a scatterplot cannot be distinguished—in fact, they all look the same—when they are compared one-by-one, rather than compared as elements of the pattern of which they are elements. Context mapping is important in statistical analysis. Coefficients that summarize relations among variables are usually misleading or uninterpretable outside the context provided by scatter plots and other visual methods in statistics (see Tufte 1983, 1997). Figure 1 illustrates how identical sets of correlation (r), goodness-of-fit (r²) and probability ( p) statistics match different patterns. Statistics are likely to be misinterpreted outside the context provided by scatterplots, each of which has its own visual signature.

2. Theory Of Pattern Matching

The first systematic effort to develop a theory and methodology of pattern matching was that of psychologist and philosopher of social science, Egon Brunswik, a professor at the University of California, Berkeley between 1935 and his death in 1955. In this period, he and his close collaborator, Edward Tolman, developed different aspects of the theory of probabilistic functionalism. To communicate this complex theory, Brunswik developed, initially for illustrative and pedagogical purposes, a lens model that was based on the optics metaphor of a double convex lens. The indispensable procedural complement of probabilistic functionalism and the lens model was his methodology of representative design.

2.1 Probabilistic Functionalism

Probabilistic functionalism is a substantive theory and methodology (philosophy of method) that focuses on relations of adaptation and accommodation between the organism and its environment. Probabilistic functionalism investigates the ways that interdependent, intersubstitutable, and uncertain cues about external environments are used to make judgments about these environments. Environments are not fully determined and uniform in their structures and processes of causality; rather they are uncertain, unstable, and causally textured (Tolman and Brunswik 1935). Probabilistic functionalism also studies the manner in which knowers learn about their environments by using informational cues or indicators, continuously creating new cues and revising or abandoning old ones. An essential aspect of these cues is that they are interdependent, multiply correlated, and intersubstitutable, features that require a process of knowing that is approximate, indirect, and vicarious. Darwinian in its focus on the adaptation of the organism to its environment, probabilistic functionalism seeks to understand how these two complex systems, the organism and the environment, come to terms with one another through a process of pattern matching.

2.2 The Brunswik Lens Model

Brunswik (1952) developed his ‘lens model’ to illustrate the probabilistic interrelations between the organism and the environment. The lens model represents processes of perception and judgment in terms of the optics metaphor of light entering (converging on) and exiting (diverging from) a double-convex lens. The lens model, while initially metaphorical in character, was later specified in what has come to be known as the ‘lens model equation’ (Slovic and Lichenstein 1971, pp. 656–67):

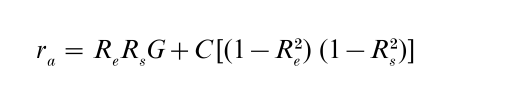
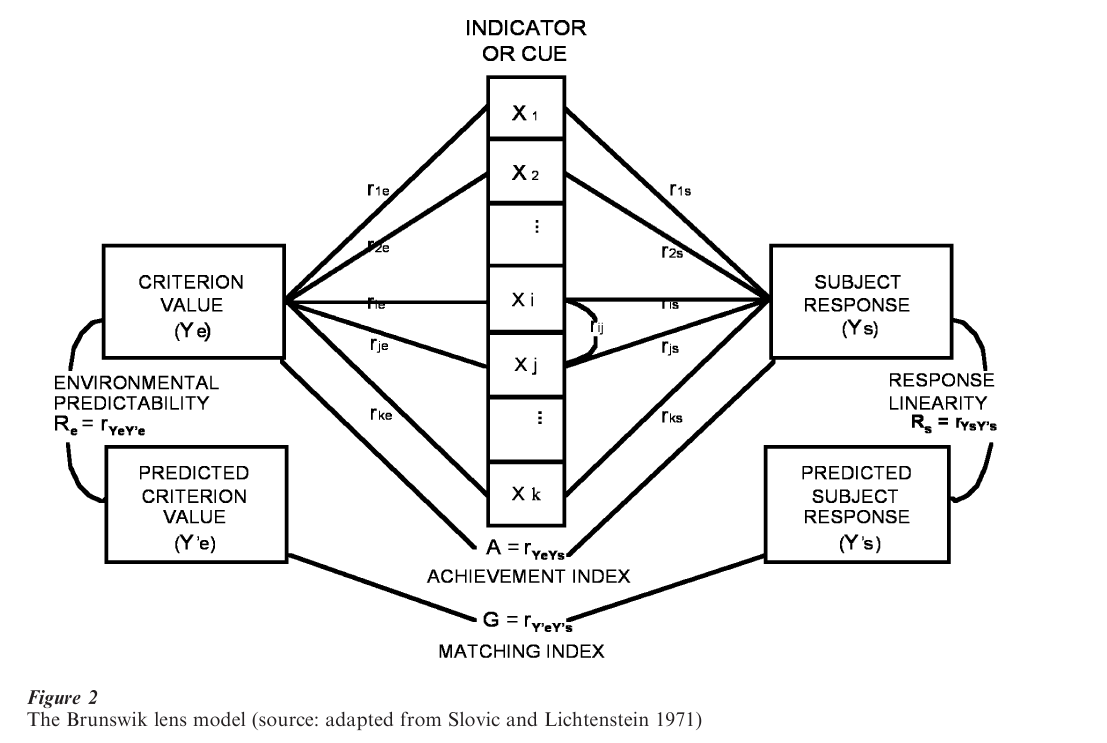
The lens model supplies an achievement index, A, which measures the extent to which pattern matching has been achieved (see figure below). The achievement index (A = r_YeYs) is the correlation between the statistical properties of an uncertain environment (Y_e) and the statistical properties of a judge’s (or knower’s) response system (Y_s). A matching index, G, is the correlation between the predicted knower’s response (Y_s´) and the predicted criterion value for the environment (Y_e´). The lens model also estimates the degree to which indicators or cues are used in a linear or nonlinear fashion. In the equation above, the coefficient, C, is the correlation of the nonlinear residual variance in the multiple correlation coefficients R_e and R_s.

2.3 Representative Design

The methodology of representative design requires that experiments be conducted in realistic settings that are representative of an organism’s typical ecology. Representative design is a radical departure from the classical experiment, in which one independent (treatment) variable is manipulated so as to assess its effect on a dependent (criterion) variable, with all other factors held constant through random subject sampling and statistical controls. Instead, experiments were to be conducted in natural settings, in environments that are unstable, dynamic, uncertain, and probabilistic. Such experiments require situation sampling, not merely the random sampling of subjects, because only the former optimizes the representative character of experiments. Representative design, in addition to its call to abandon the classical experiment, also required a rejection of the uniformity of nature presumption underlying Mill’s Canons. Both ignored, and therefore failed to account for, the effects of the many interrelated contingencies that are causally relevant to experimental outcomes. Significantly, although Brunswik was an active participant in the Unity of Science Movement, and thus to some degree seems to have identified with logical positivism, he rejected the uncritical imitation of physics promoted by Vienna Circle positivists and the bulk of psychologists of his time. Psychology, and by extension other social and behavioral sciences, was practicing ‘emulative physicalism’ in its attempt ‘to copy not only the basic methodological principles but also the specific thematic content of physics, thus nipping in the bud the establishment of (appropriate) methodological directives’ (Brunswik 1952, p. 36; quoted in Hammond 1966, p. 55).

3. Methodology Development

Probabilistic functionalism and representative design have influenced the contributions of several highly influential scholars who studied with Brunswik and Tolman at Berkeley. Some of these contributions are principally theoretical, for example, social judgment theory (Hammond 1980) and evolutionary epistemology (Campbell 1974, 1996). It is in the area of methodology development, however, where many of the most important contributions have been made.

3.1 The Lens Model And Clinical Inference

The lens model, backed by probabilistic functionalism and representative design, has been at the center of an entire research tradition on clinical inference (see Hammond 1980, 1996). Significantly, many of the most important lens-model studies have been applied studies conducted with the aim of improving learning, judgment, and behavior. In this tradition, research problems have turned on the question of how pattern matching can explain differences in achievement (predictive accuracy) among individuals with different levels of experience, including novices as well as experts. The right side of the lens model (Fig. 2) is used to predict a ‘distal’ environmental variable (e.g., future university enrollments) by regressing individual judgments about the distal variable on a set of interrelated and mutually substitutable informational cues (e.g., unemployment, income per capita, changes in age structure. In turn, the left side of the model focuses on predictions of that same distal variable derived from a multiple regression analysis in which the same cues (although here they are ‘indicators’ or ‘variables’) are predictors.

An important variant of this basic design is one where members of different professional groups—for example, scientists and lawyers in some area of science policy—occupy the right and left sides of the lens model. Either group may be taken as a reference class, and the calculation of the matching index, M, expresses the degree to which their prediction patterns match. In applied contexts, the judgments of each participant (subject) are externalized and made available to other participants. In addition, the way that each participant uses information (e.g., in a linear or nonlinear fashion) is estimated through a process of ‘policy capturing.’ These and other applications of the lens model have been designed to improve learning and judgments in contexts ranging from R&D planning, police work, gun control, and human factors research. The lens model has a computerized decision support program (‘Policy PC’) and its theoretical foundation has been redefined from social judgment theory to Cognitive continuum theory (Hammond 1996).

3.2 Methodological Triangulation

The recognition that nature is not directly observable—that our predicament as knowers is that we must employ many intercorrelated and mutually substitutable proximal cues to infer the properties and behavior of distal objects—means that science and other forms of ‘distal knowing’ involve a process of pattern matching through triangulation (Campbell 1966). A number of important methodologies were developed on the basis of this recognition. One of these is the substitution of definitional operationism with multiple operationism, a substitution that involves triangulation among two or more operational definitions, each of which is seen as approximate, fallible, and independently imperfect. A second development was the expansion of multiple operationism to include theoretical constructs as well as methods for their measurement. Here the multitrait-multimethod matrix reconceptualized construct validity as a ‘traitmethod unit,’ and introduced the concepts of convergent validity (multiple measures of the same construct should converge) and discriminant validity (multiple measures of different constructs should diverge) that parallel aspects of Brunswik’s metaphor of a double-convex lens. The 1959 article in which the multitrait-multimethod matrix was first published (Campbell and Fiske 1959) is reputed to be one of the most highly cited in the social and behavioral sciences. A third development is multiple triangulation, including critical multiplism (Cook 1984), which involves the inclusion of multiple theories, methods, measures, observers, observations, and values. These and other forms of methodological triangulation enable ‘strong inference’ in the natural and social sciences (Platt 1964) and affirm that the vast bulk of what is known is based on processes of indirect, vicarious learning.

3.3 Quasi-Experimental Design

The methodology of representative design, as we have seen, rejected the classical experiment on grounds that it is unrepresentative of the usual ecology of in which knowers function. Representative design was carried forward into the applied social sciences by Donald T. Campbell and associates (Campbell and Stanley 1963, Cook and Campbell 1979). Their quasi-experimental designs were contrasted with the classical laboratory experiments in which: an outcome variable is explained by a single independent (treatment) variable (the so-called ‘rule of one’); other possible explanations are ruled out through random selection of subjects; and the experimenter has virtually complete control over all contingencies. Quasi-experimentation, although it may use some of the features of classical experiments (e.g., repeated measures and control groups) should be contrasted with experiments in the analysis of variance tradition of Ronald Fisher, who envisioned experimenters who ‘having complete mastery can schedule treatments and measurements for optimal statistical efficiency, with the complexity of design emerging only from that goal of efficiency. Insofar as the designs discussed in the present chapter become complex, it is because of the intransigency of the environment: because, that is, of the experimenter’s lack of complete control’ (Campbell and Stanley 1963, p. 1).

Because quasi-experimental designs are intended for research in settings in which numerous contingencies are beyond the control of the experimenter, many rival hypotheses (alternative explanations of the same outcome) can threaten the validity of causal claims. These rival hypotheses are organized in four sets labeled threats to statistical conclusion, internal, external, and construct validity (Cook and Campbell 1979, Chap. 2). Plausible rival hypotheses must be tested and, where possible, eliminated. This process of eliminative induction is a qualified form of Mill’s joint method of agreement and difference and Karl Popper’s falsificationist program. Quasi-experimentation is part of a wider evolutionary critical-realist epistemology (see Campbell 1974, Cook and Campbell 1979, Shadish et al. 2000) according to which knowers adapt to real-world environments by using overlapping and mutually substitutable informational sources to test and improve their knowledge of indirectly observable (distal) objects and behaviors. Quasi-experimentation is a form of pattern matching.

3.4 Pattern-Matching Case Studies

When quasi-experimental designs are unfeasible or undesirable, several forms of case study analysis are available. Each of these involves pattern matching.

(a) Theory-Directed Case Study Analysis. When a well-specified theory is available, a researcher can construct a pattern of testable implications of the theory and match it to a pattern of observations in a single case (Campbell 1975). Using statistical ‘degrees of freedom’ as a metaphor, the theory-directed case study is based on the concept of ‘implications space,’ which is similar to ‘sampling space.’ Testable implications are functional equivalents of degrees of freedom, such that the more implications (like a larger sample) the more confident we are in the validity of the conclusions drawn. But because theories are almost inevitably affected by the culturally acquired frames of reference of researchers, the process of testing implications should be done by at least two ‘ethnographers’ who are foreign to and native to the culture in which the case occurs. The process of triangulation among observers (ethnographers) can be expanded to include two (or more) cases.

(b) Qualitative Comparative Case Study Analysis. Two or more cases are compared by first creating a list of conditions that are believed to affect a common outcome of interest (see Ragin 1999, 2000). The multiplication rule, r^m is used to calculate the number of possible ordered configurations of r categories, given m conditions. When r = 2 and m = 4, there are 2⁴ = 16 configurations, each of which may involve causal order. These configurations become the rows in a ‘truth table,’ and each row configuration is sequentially applied to an outcome with r categories (e.g., successful vs. unsuccessful outcome). Because this method examines possible configurations, and two or more different configurations may explain the same outcome in different cases, the qualitative comparative method should be contrasted with traditional (tabular) multivariate analysis. The qualitative comparative method matches configurable patterns that have been formally structured by means of set theory and Boolean algebra against patterns of observations in case materials.

(c) Modus Operandi Analysis. When quasi-experimental research is not possible, modus operandi methods (see Scriven 1975) may be appropriate for making causal inferences in specific contexts. Modus operandi methods are based on the analogy of a coroner who must distinguish symptoms and properties of causes from the causes themselves. The first step is to assemble a list of probable causes, preferably one that is quasi-exhaustive. The second is to recognize the pattern of causes that constitutes a modus operandi— modus refers to the pattern, while operandi refers to specific and ‘real’ causes. The modus operandi of a particular cause is its characteristic causal chain, which represents a configuration of events, properties, and processes. Modus operandi analysis has been formalized, partially axiomatized, and advanced as a way to change the orientation of the social and behavioral sciences away from abstract, quantitative, predictive theories toward specific, qualitative, explanatory analyses of causal patterns (Scriven 1974, p. 108).

4. Conclusion

To date, the only thorough and systematic theory of pattern matching is that of probabilistic functionalism and its methodological complement, representative design. Pattern matching is essential for achieving knowledge of external objects and events, of causal regularities that have been repeatedly recognized as the same, of the character of discrete observations formed by viewing them in context, of the fit between a curve and a set of data points, of the extent to which theories cohere, and of the degree to which theory and data correspond. Underlying all pattern matching methodologies is a shared recognition that knowing in science is profoundly indirect, vicarious, and distal.

Bibliography:

1. Alcoff L M 1996 Real Knowing: New Versions of the Coherence Theory of Truth. Cornell University Press, Ithaca, NY
2. Anscombe F J 1973 Graphs in statistical analysis. American Statistician 27: 17–21
3. Ayer A J 1936 Language, Truth, and Logic. Golanc, London
4. Brunswik E 1956 Perception and the Representative Design of Psychological Experiments, 2nd edn. University of California Press, Berkeley, CA
5. Brunswik E 1952 The Conceptual Framework of Psychology. University of Chicago Press, Chicago
6. Campbell D T 1959 Methodological suggestions for a comparative psychology of knowledge processes. Inquiry 2: 152–82
7. Campbell D T 1966 Pattern matching as an essential in distal knowing. In: Hammond K R (ed.) The Psychology of Egon Brunswik. Holt, Rinehart, and Winston, New York
8. Campbell D T 1974 Evolutionary epistemology. In: Schilpp P A (ed.) The Philosophy of Karl Popper. Open Court Press, La Salle, IL
9. Campbell D T 1975 ‘‘Degrees of Freedom’’ and the case study. Comparative Political Studies 8: 178–93
10. Campbell D T 1986 Science’s social system of validity-enhancing collective belief change and the problems of the social sciences. In: Fiske D W (ed.)
11. Campbell D T 1988 Methodology and Epistemology for Social Science: Selected Papers. University of Chicago Press, Chicago
12. Campbell D T 1996 From evolutionary epistemology via selection theory to a sociology of scientific validity. Evolution and Cognition
13. Cook T D, Campbell D T 1979 Quasi-Experimentation: Design & Analysis Issues for Field Settings. Houghton Mifflin, Boston
14. Hammond K R (ed.) 1966 The Psychology of Egon Brunswik. Holt, Rinehart, and Winston, New York
15. Hammond K R 1980 Human Judgment and Decision Making: Theories, Methods, and Procedures. Praeger, New York
16. Hammond K R 1996 Human Judgment and Social Policy: Irreducible Uncertainty, Inevitable Error, Unavoidable Injustice. Oxford University Press, New York
17. Putnam H 1981 Reason, Truth, and History. Cambridge University Press, Cambridge, UK
18. Quine W V 1951 Two dogmas of empiricism. Philosophical Review 60(1): 20–43
19. Ragin C C 1999 Using comparative causal analysis to study causal complexity. HSR: Health Services Research 34(5), Part II
20. Ragin C 2000 Fuzzy-Set Social Science. University of Chicago Press, Chicago
21. Rescher N 1980 Induction: An Essay on the Justification of Inductive Reasoning. University of Pittsburgh Press, Pittsburgh, PA
22. Schweder (eds.) Metatheory in Social Science: Pluralisms and Subjectivities. University of Chicago Press, Chicago
23. Scriven M 1975 Maximizing the power of causal investigations: The modus operandi method. In: Glass G V (ed.) Evaluation Studies Review Annual. Sage Publications, Beverly Hills, CA, Vol. 1
24. Shadish W, Cook T, Campbell D T 2000 Quasi-Experimentation. Houghton Mifflin, Boston
25. Slovic P, Lichtenstein S 1971 Comparison of bayesian and regression approaches to the study of information processing in judgment. Organizational Behavior and Human Performance 6(6): 649–744
26. Trochim W 1990 Pattern matching and psychological theory. In: Chen R (ed.) Theory-Driven Evaluation. Jossey Bass, San Francisco