Dimensionality Of Tests Research Paper

The concept of unidimensionality is a specific instance of the principle of local independence—that is, the existence of one latent trait underlying the data. The principle of local independence requires that responses to different items are uncorrelated when θ (the person’s ability) is fixed, although it does not require that items be uncorrelated over groups in which θ varies. Lord and Novick (1968) gave the definition of local independence more substantive meaning by writing that:

an individual’s performance depends on a single underlying trait if, given his value on that trait, nothing further can be learned from him that can contribute to the explanation of his performance. The proposition is that the latent trait is the only important factor and, once a person’s value on the trait is determined, the behavior is random, in the sense of statistical independence ( p. 538).

A set of items can be said to be unidimensional when it is possible to find a vector of values θ = (θi) such that the probability of correctly answering an item k is πik=fk(θi) and local independence holds for each value of θ. This definition is not equating unidimensionality with local independence, because it can further require that it is necessary to condition only on one θ dimension and that the probabilities p_ik can be expressed in terms on only one θ dimension.

McDonald (1981) outlined ways in which it is possible to weaken the strong principle of local independence. The strong principle implies that not only are the partial correlations of the test items zero when the latent traits are partialled out, but also the distinct items are then mutually statistically independent and their higher joint moments are products of their univariate moments. A weaker form is to ignore moments beyond the second order and test the dimensionality of test scores by assessing whether the residual covariances are zero (see also Lord and Novick 1968, pp. 225, 544–5). Under the assumption of multivariate normality, the weaker form of the principle implies the strong form, as well as conversely. McDonald (1979, 1981) argued that this weakening of the principle does not create any important change in anything that can be said about the latent traits, though strictly it weakens their definition.

1. Stout’s Evaluation Of Essential Unidimensionality

Stout (1987, 1990) also used this weaker form to develop his arguments for ‘essential unidimensionality.’ He devised a statistical index based on the fundamental principle that local independence should hold approximately when sampling from a subpopulation of examinees of approximately equal ability. He defined essential unidimensionality as: a test (U₁,…, U_N) of length N is said to be essentially unidimensional if there exists a latent variable θ such that for all values of θ,

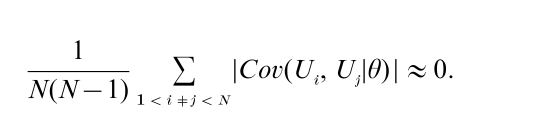
That is, on average, the conditional covariances over all item pairs must be small in magnitude (for more detail regarding the theoretical developments see Junker 1990, 1991, 1992, Nandakumar 1994, Nandakumar and Stout 1993, Stout 1990). Essential unidimensionality thus replaces local independence and is based on assessing only the dominant dimensions. Stout has developed an empirical notion of unidimensionality to match his weaker form (Stouts Tindex). There are many applications of Stout’s procedures (Nandakumar 1994, Nandakumar et al., 1998), and simulation studies that have supported the value of his statistic (Hattie et al. 1996). Zhang and Stout (1999a, 1999b) have generalized the Stout procedure via the DETECT method (Dimensionality evaluation to enumerate contributing traits). This method simultaneously assesses the latent dimensionality structure and determines the degrees of multidimensionality present in test data. This procedure has been extended by Kim et al. (Douglas et al. 1998, Stout et al. 1996) to identify that partition P of the available k items into disjoint and exhaustive subsets that best represents the underlying dimensionality structure. The best partition is detected by DETECT_max, and thus is a measure of the amount of departure from unidimensionality. The methods have been generalized to polytomous items (Nandakumar et al. 1998).

Thus, there are many methods for assessing unidimensionality, such as nonlinear factor analysis (NOHARM), full information item factor analysis (TESTFACT), confirmatory factor analysis via structural equations programs such as LISREL, AMOS, and testing essential dimensionality with DIMTEST, and detection of simple structure multidimensionality (DETECT).

2. The Concept Of Unidimensionality

It is critical to note that the assumption of unidimensionality underlying most measurement models does not necessarily imply that only these models can assess the most simple of tasks. The concept of unidimensionality can be considered at various levels of analysis. At the first-order level we can construe of a set of items being combined (by appropriate weighting) to form a total unidimensional score (such as a collection of addition items leading to a total addition score). At the second-order level we can also construe of a set of first-order scores being combined to form a total undimensional score (such as a collection of addition, subtraction, multiplication, and division totals being combined to form a total arithmetic score). In both cases we can conceive of a single underlying trait.

In a different context, we could imagine a single set of items all requiring a similar cognitive process (e.g., successive or simultaneous processing) and a total score being formed—and we could consider this a unidimensional total score—even if the items were across many content domains. All too often, the notion of unidimensional has been conceived in terms of a narrowly defined set of items. The key issue is that the methods outlined to assess unidimensionality do not lead to identifying what the total score represents—this requires other validity methods (such as judgmental analyses). Identifying a unidimensional set of items is not the same as naming it.

3. Constructing Multidimensional Data

One of the problematic issues when assessing dimensionality is that there are differing ways that the dimensions can relate to the construct of interest. Coombs (1954) defined three methods of constructing multidimensional data: the conjunctive model, whereby an excess of one ability, no matter how large, does not compensate for lower ability in other dimensions; the disjunctive model, whereby an examinee will pass an item if he/she is dominant over the item in any one dimension and will fail only if the item dominates him/her in all dimension; and the compensatory model, whereby an examinee’s response to an item is a function of a weighted sum of underlying abilities. Other researchers (notably Ackerman 1987, 1992, Ansley and Forsyth 1985, Reckase et al. 1986, Wang 1987, 1988) have demonstrated that with compensatory multidimensional models the univariate calibration of two-dimensional response data can be explained in terms of the interaction between the multidimensional test information and the distribution of the two-dimensional abilities, and various interpretations of the multidimensional item difficulty, multidimensional discrimination, and multidimensional item information have been suggested.

Sympson (1978) proposed a partially compensatory model where a decrease in one ability could only be offset by a large increase in the other ability (this model has often been erroneously called a noncompensatory model). Outside of a relatively narrow ability range, the probability of passing reduces to zero regardless of the value of the stronger ability (see Lord 1984). The probability of a correct response is simply the product of probabilities for each dimension (but see Coughlan 1974, Jannarone 1986).

4. Concluding Comments

A major need is for a clear explication of the concept of dimensionality. Within the item response literature there has been much agreement about its meaning, although it has often been (falsely) assumed that only tests consisting of ‘simple’ attributes could lead to a unidimensional test. Certainly there are cognitive processing models, whereby it may be possible for a student to solve an item using differing cognitive strategies, thus adding another meaning to the notion of undimensional; the unidimensionality of processes or strategies. Much of the discussion about newer models of item and test analyses is oriented around such notions (Mislevy and Gitomer 1995).

It is critical to ensure that any set of items map the construct of interest, and if this construct is inherently multidimensional than so too should there be multiple unidimensional subtests. At this test score level, we may desire ‘lumpy’ items (such as reading comprehension, or mathematical problem solving), and thus the items may assess multiple dimensions while the total test still aims to assess a single ‘over all’ dimension. As Dorans and Lawrence (1999) have demonstrated, it is possible to conceive of situations where analysis at the test score level would reveal a single common factor, while analysis at the subscore level would uncover a few distinct subscore factors. Similarly, Reckase et al. (1988) have demonstrated that sets of items can meet the unidimensionality assumption even though they require more than one proficient for a correct response.

At present, the Stout procedures seem worth pursuing, as they are based on clear theoretical developments, are easy to use, dependably provide indications of the dimensionality, are reasonably robust, and provide a reasonably clear and practical demarcation between one and many dimensions. Further, there is need for further research on developing multidimensional models that allow for differing ways in which items or test scores can be combined, and we need better diagnostics to understand the complexity of the dimensions involved in item and test scores. There are already many useful heuristics available to interpret multidimensional data using unidimensional calibration methods (Ackerman 1992, Carlson 1987, Junker 1991, 1992, Luecht and Miller 1991, McKinley and Reckase 1989, Reckase et al. 1986, 1988). It is certain that discussion will continue about the concept of unidimensionality, the best forms to assess whether items are essentially unidimensional, and the importance of diagnostics to aid in constructing better unidimensional assessments.

Bibliography:

1. Ackerman T 1987 The Robustness of LOGIST and BILOG IRT Estimation Programs to Violations of Local Independence. American College Testing Program, Iowa City, IA
2. Ackerman T A 1992 A didactic explanation of item bias, item impact, and item validity from a multidimensional perspective. Journal of Educational Measurement 29: 67–91
3. Ansley R A, Forsyth T N 1985 An examination of the characteristics of unidimensional IRT parameter estimates derived from two-dimensional data. Applied Psychological Measurement 9: 37–48
4. Carlson J E 1987 Multidimensional Item Response Theory Estimation: A Computer Program. American College Testing Program, Iowa City, IA
5. Coombs C H 1954 A Theory of Data. Wiley, New York
6. Coughlan J R 1974 A Multidimensional Extension of the Normal Ogive, Logistic and Linear Latent Trait Model. Unpublished Master’s thesis, University of Toronto
7. Dorans N J, Lawrence I M 1999 The Role of the Unit of Analysis in Dimensionality Assessment. (Educational Testing Service Report, No. 99–14). Princeton, NJ
8. Douglas J, Kim H R, Habing B, Gao F 1998 Investigating local dependence with conditional covariance functions. Journal of Educational and Behavioral Statistics 23(2): 129–51
9. Hattie J A 1985 Methodology review: Assessing unidimensionality of tests and items. Applied Psychological Measurement 9: 139–64
10. Hattie J A, Krakowski K, Rogers H J, Swaminathan H H 1996 An assessment of Stout’s index of essential unidimensionality. Applied Psychological Measurement 20: 1–14
11. Jannarone R J 1986 Conjunctive item response theory kernels. Psychometrika 51: 357–3
12. Junker B W 1990 Progress in Characterizing Strictly Unidimensional IRT Representations. Technical Report 498, Department of Statistics, Carnegie Mellon University, Pittsburgh, PA
13. Junker B W 1991 Essential independence and likelihood-based ability estimation for polytomous items. Psychometrika 56: 255–78
14. Junker B 1992 April Ability Estimation in Unidimensional Models When More Than One Trait is Present. Paper presented at the Annual Meeting of the American Educational Research Association, San Francisco, CA
15. Lord F M 1984 Conjunctive and disjunctive item response functions. (Educational Testing Services Report, No. 150–520). ETS, Princeton, NJ
16. Lord F M, Novick M R 1968 Statistical Theories of Mental Test Scores. Addison-Wesley, Reading, MA
17. Luecht R M, Miller T R 1991 Unidimensional Calibrations and Interpretations of Multidimensional Tests. Paper presented at the Annual Meeting of the National Council on Measurement in Education, Chicago, IL
18. McDonald R P 1979 The structural analysis of multivariate data: A sketch of general theory. Multivariate Behavioural Psychology 14: 21–38
19. McDonald R P 1981 The dimensionality of tests and items. British Journal of Mathematical Statistical Psychology 34: 100–117
20. McKinley R L, Reckase M D 1983 MAXLOG: A computer program for estimating the parameters of a multidimensional extension of the two-parameter logistic model. Behavior Research Methods and Instrumentation 15: 389–90
21. Messick S 1989 Validity. In: Linn R L (ed.) Educational Measurement, 3rd edn. Macmillan, New York, pp. 13–103
22. Mislevy R J, Gitomer D H 1995 The role of probability-based inference in an intelligent tutoring system. User Modeling & User-Adapted Interaction 5: 253–82
23. Nandakumar R 1991 Traditional dimensionality vs. essential dimensionality. Journal of Educational Measurement 28: 99–
24. 117
25. Nandakumar R 1994 Assessing latent trait unidimensionality of a set of items—comparison of different approaches. Journal of Educational Measurement 31: 1–18
26. Nandakumar R, Stout W 1993 Refinements of Stout’s procedure for assessing latent trait unidimensionality. Journal of Educational Statistics 18: 41–68
27. Nandakumar R, Yu Z Y, Li H H, Stout W 1998 Assessing unidimensionality of polytomous data. Applied Psychological Measurement 22: 99–115
28. Reckase M D, Ackerman T A, Carlson J E 1988 Building a unidimensional test using multidimensional items. Journal of Educational Measurement 25: 193–203
29. Reckase M D, Carlson J E, Ackerman T A, Spray J A 1986 The Interpretation of Unidimensional IRT Parameters when Estimated from Multidimensional Data. Paper presented at the Psychometric Society Annual Meeting, Toronto
30. Stout W F 1987 A nonparametric approach for assessing latent trait unidimensionality. Psychometrika 52: 589–617
31. Stout W F 1990 A new item response theory modelling approach and applications to unidimensionality assessment and ability estimation. Psychometrika 55: 293–325
32. Stout W, Habing B, Douglas J, Kim H R 1996 Conditional covariance-based nonparametric multidimensionality assessment. Applied Psychological Measurement 20(4): 331–54
33. Tam S S 1992 A Comparison of Methods for Adaptive Estimation of a Multidimensional Trait. Unpublished doctoral dissertation, Graduate School of Arts and Sciences, Columbia, NY
34. Wang M M 1987 Estimation of Ability Parameters from Response Data to Items that are Precalibrated with a Unidimensional Model. Paper presented at the Annual meeting of the American Educational Research Association, Washington, DC
35. Wang M M 1988 Measurement Bias in the Application of a Unidimensional Model to Multidimensional Item-response Data. Paper presented at the Annual meeting of the American Educational Research Association, New Orleans, LO
36. Yu F, Nandakumar R in press Poly-Detect for quantifying the degree of multidimensionality. Journal of Educational Measurement
37. Zhang J, Stout W 1999a Conditional covariance structure of generalized compensatory multidimensional items. Psychometrika 64(2): 129–52
38. Zhang J, Stout W 1999b The theoretical DETECT index of dimensionality and its application to approximate simple structure. Psychometrika 64(2): 213–49