Ordered Relational Structures Research Paper

Many of the phenomena for which one needs measurements exhibit some kind of dominance, preference, or ordering. Therefore, most of the relational structures which are used in measurement theory carry some kind of abstract ordering relation (linear, weak, or partial orders).

In short, an ‘ordered relational structure’ consists of a base-set, here always denoted by A, an order relation on A, and possibly further relations on A. It is the foundation on which representational measurement theory is built. Sometimes A is the Cartesian product of other sets, sometimes it is the union of disjoint sets and some of the relations are between these sets (see Sect. 1 for definitions). While the investigation of one such structure may be a part of mathematics, in applications in the behavioral and social sciences the common frame consists of at least two relational structures, one to describe in a qualitative way the investigated part of reality and the other a formal, mathematical, or numerical structure that is well understood or that can be investigated by means of mathematics, logic, or computation. Such a development can yield results relevant to the empirical subject under scrutiny if the investigator succeeds in faithfully mapping the qualitative structure into the formal structure.

1. Relations, Functions, Operations

Let A and B be two sets. The ‘Cartesian product’ of these sets is denoted by A×B and consists of all ordered pairs (a, b) with a ϵ A and b ϵ B. Any subset R C A × B is called a ‘binary relation’ between A and B. The case A = B is of particular interest; in this situation R is called a ‘relation’ on A. Clearly, this construction can easily be generalized to a k-ary relation, denoting a subset of the Cartesian product of k sets, i.e., R C A₁ × A₂ ×…× A_k. If in this case all sets A_i equal A, then the Cartesian product is denoted as A^k and R is a k-ary relation on A. This broad concept is often used to describe parts of mathematics, mostly with further restrictions and properties on R, but it is also possible to use it in everyday situations. For example, let A be a set of persons and let (a, b) ϵ R denote the fact that a and b have the same birthday. Or if A is the set of participants in a tournament and (a, b) ϵ R denotes the result ‘a beats b’, then R is an encoding of the outcome of this tournament.

We now classify the possible relations. Among the ‘binary relations’ there is the prominent class of ‘order relations.’ In this research paper we only consider weak and linear orders, denoted by ≤. A ‘weak order’ satisfies by definition ‘transitivity,’ i.e., a ≤ b and b ≤ c implies a ≤ c, and ‘completeness,’ i.e., for all a, b ϵ A holds a ≤ b or b ≤ a. A ‘linear order’ is a weak order satisfying ‘anti-symmetry,’ i.e., for all a, b ϵ A holds, if a ≤ b and b ≤ a then a = b.

Now we are ready to define an ‘ordered relational structure.’ It consists of a nonempty set A, a weak order ≤ on A, and possibly more relations R_i with i ϵ I for some index set I. In the sequel an ordered relational structure is denoted by

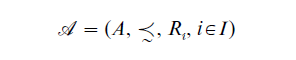
If R_i is a k_i-ary relation, then (k_i, i ϵ I ) is the type of the structure.

Closely related to order relations are ‘equivalence relations.’ Such a relation ~ satisfies by definition ‘reflexivity,’ i.e., a ~ a, ‘symmetry’ i.e., a ~ b implies b ~ a, and transitivity. A set on which an equivalence relation is defined can be partitioned into disjoint subsets of equivalent elements. These subsets are called ‘equivalence classes.’ Often one can reduce a structure by replacing the base set A with the set of its equivalence classes.

There are a few operations on relations that can be employed to generate new relations. We define them only for binary relations on a set A. Thus, in what follows R, S C A × A.

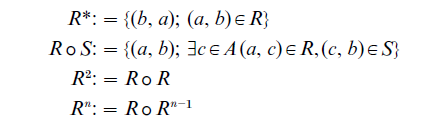
Thus, if (a, b) ϵ R means ‘a beats b in a tournamen t’ then (a, b) ϵ R* means ‘a is beaten by b,’ and aR²b means ‘a has beaten someone who in turn has beaten b.’

Mappings between two sets A, B are a particular kind of binary relation. A relation f between A and B is a ‘mapping’ (or ‘function),’ when, for all a ϵ A there is exactly one b ϵ B such that (a, b) ϵ f. In this case one writes f (a) = b rather then (a, b) ϵ f. The comprehensive notation is

A is called the ‘domain’ and B the ‘range’ of f. If b = f (a) then b is the image of a (under f ) and a is a pre-image of b (there may be more than one). For a subset A´ of A the set of images of all a ϵ A´ is denoted by f (A´). In particular f (A) = {b ϵ B; there is an a ϵ A such that f (a) = b}. A mapping is ‘surjective’ if f (A) = B and ‘injective’ if f (a₁) = f (a₂) implies a₁ = a₂. Thus, an injective function allows at most one pre-image of each element in its domain. An injective and surjective function is called ‘bijective’ or a ‘bijection.’ Bijective functions can be ‘inverted;’ this concept denotes the function f ⁻¹: B → A such that f ⁻¹ (b) = a if f (a) = b.

Sometimes bijections f : A → A are called ‘permutations.’ For instance, when dealing with finite sets this terminology is quite usual. Under these bijections there is one which is particularly simple, the identity mapping, denoted by id_A. It is defined by id_A: A → A and id_A (a) = a for all a ϵ A.

Functions can be ‘concatenated,’ i.e., if f : A → B and g: f (A) → C then g f: A → C by setting g o f (a): = g( f (a)). Note that the order of f, g in g o f is important—f o g is not always defined and if it is, e.g., if A = f (A) = C, then in general f o g = g o f. One has f o id_A = f and id_f(A) o f = f. If f is bijective then f ⁻¹ o f = id_A and f o f ⁻¹ = id_B.

If the respective conditions on the domains and ranges are met then the -operation of functions is ‘associative,’ i.e., h o (g o f ) = (h o g) o f. Thus, the brackets can be omitted, and we simply write h o g o f.

Mathematical operations such as addition of real numbers are special functions. A ‘(binary) operation’ • on A is a function.

Thus, it is a special kind of ternary (i.e., 3-ary) relation. It is a ‘partial’ operation if its domain is a proper subset of A × A. Examples of structures with operations frequently occur in measurement theory under the name ‘extensive’ or ‘positive concatenation’ structures.

An operation is ‘associative’ if a ● (b ● c) = (a ● b) ● =c. Sometimes the notion of ‘weak associativity’ is needed. If a ~ b denotes a ≤ b and b ≤ a then the operation ● is weakly associative if a ● (b ● c) ~ (a ● b) ● c. As already mentioned, weak association might arise in a structure (A, ≤, ●), where ≤ is a weak order.

It should be noted in passing that the relation defined in the previous paragraph is an equivalence relation. It is often used if one wants to replace a given weak order by a linear order.

2. Examples Of Ordered Relational Structures

2.1 Weights

Consider a collection of weights and let a ≤ b stand for: If a is put in one pan of a balance and b in the other, then the one containing b remains in place or deflects the pointer to b’s side. Let a ● b denote putting a and b in one pan. Let A denote the set of all weights and of all combinations that can be formed by putting two or more of the weights in one pan. It can be assumed, with reasonable accuracy that (A, ≤, ●) is an ordered relational structure. Furthermore, the operation ● will be approximately weakly associative and positive, i.e., a < a ● b for all b ϵ A (x < y is short for x ≤ y and not y ≤ x). Still more, it will satisfy ‘commutativity’ a ● b = b ● a.

2.2 Guttman Scaling

Let A be a set of testees and B a set of items to be solved by each a ϵ A. For a ϵ A and b ϵ B let aRb denote that person a fails to solve item b correctly. Now assume that the relation R (which is between A and B) satisfies

The system (A, B, R) is not an ordered relational structure in the sense of the previous section because R, being a biorder, is not a weak order on one of the sets A, B. However, we can easily construct an ordered relational structure from it. Let C: = A U B and on C define: for a, a` ϵ A a ≤ a` if person a solves at least as many items as does person a, and for b, b` ϵ B define b ≤ b` if b is solved by at most as many persons as b. Finally define a ≤ b if aRb, and b ≤ a if not aRb. Then it can be shown that ≤ is a weak order on C; thus, (C, ≤) is an ordered relational structure.

2.3 Several Orders On One Set

Let S be a collection of different societies. Assume they can be weakly ordered with respect to social mobilization (relation K ) and social frustration (relation L) of its members, and also with respect to economic development (relation M ).

This is a case of a structure A: = (A, K, L, M ) where K, L, M are all weak orders on A. Let the weak orders satisfy the following compatibility relations: For all a, b ϵ A

Suck (1990) has shown that such a structure can be transformed to an ordered relational structure on a Cartesian product which turns out to be a conjoint measurement structure satisfying independence. As an application of such a structure Suck and Getta (1994) gave an axiomatization and representation of Coombs’s portfolio theory in which A is a set of gambles (wins and losses with certain probabilities), K is an ordering of these gambles according to preference to play such gambles by subjects, L is an ordering by expected value, and M is an ordering by perceived riskiness of the gambles. The possibility to associate this situation with conjoint measurement proved very helpful in analyzing the structure and data.

Wille and Wille (1993) considered similar relational structures. They investigated the possibility of homo-morphically mapping a structure satisfying Eqns. (1), (2), and (3) into the reals without the detour via conjoint measurement. They related their investigation to the ‘Huntington controversy’ arising from Huntington (1968) who presented ‘equations’ such as:

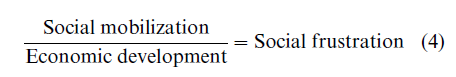
This use of ‘equations’ was severely criticized, mainly with the argument that the variables of the equation are not measurable entities. Formulating the structure in the above way can provide the means to solve this controversy. Either applying conjoint measurement in the sense of Suck (1990) or the results of Wille and Wille (1993) would yield a framework in which a decision on the validity of Eqn. (4) is possible.

3. Homomorphisms, Isomorphisms

It is often useful and even necessary to consider several relational structures at the same time. In this case it is important to describe how similar these structures are, and how one can go from one structure to the next or—more intuitively—how one can transfer knowledge from one structure to another. Examples of this technique occur in measurement theory where usually one structure has as its base set (a subset of ) the reals, or more generally, when there is one structure which is thoroughly investigated and all or many of its properties are well known. In such cases it is without doubt helpful to compare such a structure to the one under empirical investigation and to point out the manner in which the two structures resemble each other.

Let A = (A, R_i, i ϵ I ) and B = (B, S_j, j ϵ J ) be two relational structures. Then a mapping φ: A → B is called a ‘homomorphism’ between A and B if the structures are of the same type (k_i, i ϵ I ) and for all i ϵI and for all (a₁, …, a_kk_i) ϵ A^ki

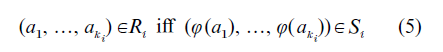
A and B are said to be ‘homomorphic’ if a homo-morphism exists between A and B, If the homomorphism is a bijection, then it is an ‘isomorphism.’ Isomorphic structures are, in a sense, identical, although their base sets A and B can be quite different, but each property of A expressible in terms of the relations R_i corresponds to a property of expressible in terms of the relations S_j.

If the structures A and B are both ordered, i.e., A = (A, ≤; R_i, i ϵ I ) and B = (B, ≤`; S_i, i ϵ I ) where ≤ and ≤ are weak orders, then the homomorphism is sometimes called ‘a monotonic’ function. It satisfies

If A is mapped homomorphically into a structure on the reals then the relation on corresponding to ≤ is usually, but not necessarily, the ≤ relation on ≤ . This situation is typical of representational measurement theory.

As an example, let R⁺ denote the positive reals and let A : = (R⁺, ≤ , •) and B: = ( R, ≤, +). Then φ(x): = log x is an isomorphism between these numerical structures.

As another example, let A be a set of players in a tournament and let ≤ denote a ranking of these players with ties allowed. Here ≤ is a weak order but in general it is not linear because of the possibility of ties. If B : = (N, ) with the natural numbers, then the mapping which associates his or her place in the ranking with each player, is a homomorphism but not an isomorphism.

Homomorphisms can be concatenated provided the range of the first and the domain of the second coincide. More precisely, let A = (A, ≤, R_i, i ϵ I ), B = (B, ≤, S_i, i ϵ I ), and E = (C, ≤, T_i, i ϵ I ) be homomorphic structures with the homomorphisms

where φ is surjective. Then A and E are homomorphic by the homomorphism ξ: = ψ o φ. This fact is of particular importance when the structures are all identical; this case is considered in Sect. 4.

4. The Automorphism Group Of An Ordered Relational Structure

An isomorphism which maps its domain structure onto itself is called an ‘automorphism.’ Let Aut A denote the set of automorphisms of a given structure A. Clearly, Aut A = 0 because id_A ϵ Aut A, i.e., the identity map is always an automorphism. If α, β ϵ Aut A then α o β ϵ Aut A; furthermore, α⁻¹ ϵ Aut A. Thus (Aut A, o) has the properties of a ‘group,’ i.e., a set with an operation on it which is associative, has an identity element (id_A in this case), and a right and left inverse (α⁻¹) Therefore (Aut A, o) is called the ‘automorphism group’ of A.

Modern measurement theory exploits the properties of the automorphism group very intensively. The main ideas on how this is done are now described.

The structure A is called ‘homogeneous’ if for each a, b ϵ A there is an α ϵ Aut A such that α (a) = b. The group and the structure are called ‘n-homogeneous’ if for any two n-tuples a₁ < … < a_n and b₁ < … < b_n there is at least one automorphism α such that α(a_i) = b_i. Similarly, they are called ‘n-unique’ if for any two n-tuples a₁ < … < a_n and b₁ < … < b_n there is at most one automorphism α such that α (a_i) = b_i. n-uniqueness can be reformulated as: if two automorphisms agree on n points then they are identical.

If M is the maximal homogeneity and N the minimal uniqueness of a structure, then the ‘scale type’ of A (or of Aut A ) is denoted by the pair (M, N ). Clearly, one has M ≤ N. N = ∞ means that there is no minimal degree of uniqueness. A structure with N < ∞ is called ‘finitely unique.’

One of the most important results of measurement theory in the 1980s is the following theorem developed by Narens (1981) and Alper (1985, 1987).

Theorem 1 (Alper/Narens Theorem)

Let A = R with A homogeneous and finitely unique.

Then it is of scale type (1, 1), (1, 2) or (2, 2).

Type (1, 1) is a ratio scale and type (2, 2) an interval scale

Suck (2000) proved a partial generalization for ordered structures with an arbitrary base set. Essentially, his result shows that for scale type (N, N), in many, though not all cases, the Alper/Narens Theorem remains true if the base set A of the structure is different from R.

5. Order Topology

If one wants to exploit the power of the continuity concept for the investigation of ordered relational structures, then one must construct a ‘topology’ on A which is compatible with the order relation and, if possible, with the other relations as well.

A topology of A is a collection T of subsets of A, called the ‘open sets,’ such that the following three conditions are satisfied:

(T1) 0 ϵ T and A ϵ T.

(T2) If J c T then U_TϵTT ϵ T.

(T3) If J is a finite subset of then also U_TϵT T ϵ T

The structure (A, T is a ‘topological space.’ For a development of the theory of topological space see Kelley (1955) or Dugundji (1966). The most important topological space is constructed on R by defining as open all subsets of R which are arbitrary unions of open intervals. This construction can be carried out in any ordered structure and is called the ‘order topology’ (see below). Thus, any A of the kind considered in this research paper can be regarded as a topological space endowed with the order topology.

In topological spaces the well-known concepts of convergence, limits, and continuity can be defined, and in this way, far reaching generalizations of familiar theorems of analysis are available in the theory of ordered relational structures.

We give the topological definition of ‘continuity.’ Let (A, T_A) and (B, T_B) be topological spaces. A function f : A → B is ‘continuous’ if for all U ϵ T_n B the preimage under f, i.e., the set f^-1 (U): = {a ϵ A; f (a) ϵ U} is in T_A.

Next, we are going to define the ‘order topology’ of an ordered structure A. We assume that A does not contain a maximal or a minimal element. We define: for all a, b ϵ A

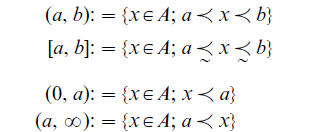
and call these sets intervals (with respect to ≤). Note that the symbols 0, ∞ do not denote elements of A.

The intervals [a, b), (a, b], (0, a], and [a, ∞) are defined analogously. (a, b), (0, a), and (a, ∞) are referred to as ‘open intervals.’ The open intervals are used as a ‘basis’ for the order topology denoted by T_∞, i.e., T_∞ is the collection of those subsets of A which can be generated by union from an arbitrary set of open intervals.

The construction of the order topology for an ordered relational structure is useful when the other relations of A are in some sense compatible with T_∞; e.g., when there is an operation among the R_i then it should be continuous.

If ≤ is a linear order, T_∞ is easily seen to separate points, i.e., for all distinct a, b ϵ A there are open and disjoint sets U, V such that a ϵ U and b ϵ V. In particular, consider a < b then, if z ϵ (a, b) exists, (0, z) and (z, ∞) are such sets; if (a, b) = 0, then (0, b) U (a, ∞) = Ø and a ϵ (0, b) and b ϵ (a, ∞). Technically, such a space is called a ‘Hausdorff space.’

A bijective and continuous map f: A → B between topological spaces (A, T_A) and (B, T_B) is a homeomorphism if its inverse is also continuous. Topology is mainly concerned with properties of spaces which are shared by all spaces that are homeomorphic to a given one. These are called ‘invariants’ of the space.

Specializing this concept on order topologies, we observe: Isomorphic linear orderings are homeomorphic with respect to the order topologies and an isomorphism is a homeomorphism. Formulating this result as a theorem one gets:

Theorem 2

Let (A, ≤ _A) and (B, ≤_B) be two linear orderings and f: A → B strictly monotonic and surjective. Then f is a homeomorphism with respect to the order topologies induced by ≤_A on A and ≤_B on B.

It follows from Theorem 2 that automorphisms of a structure A = (A, ≤, R_i, i ϵ I ) are homeomorphisms of (A, T_∞) onto itself.

Summarizing, we note that the order topology carries a lot of information about an ordered relational structure. Despite this fact, it has not been used very much in measurement theory until very recently. Wakker (1988) pointed out that in many cases the algebraic conditions used by Krantz et al. (1971) and others are more general than topological ones. As long as the use of topological concepts is restricted to the order topology no extra conditions need be imposed. In some modern investigations the order topology could be put to use as a fruitful tool. For instance, even the topological properties of the automorphism group can play an important role (Suck 1998, 2000).

Finally, it should be mentioned that the power of topological methods shows up in infinite structures (although the definitions are not restricted to this case). Some approaches to measurement try to avoid such structures, especially the continuum. As an example, we refer to Sommer and Suppes (1997).

6. Completion Of Structures

The ‘McNeille completion’ of a partial order is also useful for ordered structures. The property of existence of infimum and supremum is equivalent to the existence of a cut element for each ‘Dedekind cut.’ It is called ‘Dedekind completeness’ (cf. Narens 1985, p. 16).

If A is an ordered relational structure then the McNeille completion of (A,≤ ) is ‘Dedekind complete.’ However, a major problem arises if one wants to extend the other relations of A, i.e., the R_i for i I, to the complete superset of A. There may exist no extension at all, or too many—more than one is already too many; Narens (1985) and Cohen (1988) investigated this problem for so-called positive concatenation structures. The results are discussed in Luce et al. (1990) in Chap. 19.4.

In the context of the order topology Dedekind completeness is equivalent to ‘connectedness’ in the topological sense, i.e., there are no two disjoint open sets U, V such that A = U U V. Ovchinnikov (1996) proved the surprising result that a homogeneous structure (A, ≤) with a linear order ≤ has either a connected order topology or each of its maximal connected subsets consist of one element only. This result has far reaching consequences for ordered relational structures and their automorphism groups. It is at the heart of Suck’s (2000) generalization of the Alper/Narens result. Thus, if a completion is feasible then many properties of the structure follow from this theory.

Bibliography:

1. Alper T M 1985 A note on real measurement structures of scale type (m, m + 1). Journal of Mathematical Psychology 29: 73–81
2. Alper T M 1987 A classification of all order-preserving homeomorphism groups of the reals that satisfy finite uniqueness. Journal of Mathematical Psychology 31: 135–54
3. Cohen M 1988 Dedekind completion of positive concatenation structures: necessary and sufficient conditions. Journal of Mathematical Psychology 32: 64–71
4. Dugundji J 1966 Topology. Allyn and Bacon, Boston
5. Huntington S P 1968 Political Order in Changing Societies. Yale University Press, New Haven, CT
6. Kelley J L 1955 General Topology. Van Nostrand, New York
7. Krantz D H, Luce R D, Suppes P, Tversky A 1971 Foundations of Measurement. Academic Press, New York, Vol. 1
8. Luce R D, Krantz D H, Suppes P, Tversky A 1990 Foundations of Measurement. Academic Press, New York, Vol. 3
9. Narens L 1981 On the scales of measurement. Journal of Mathematical Psychology 24: 249–75
10. Narens L 1985 Abstract Measurement Theory. MIT Press, Cambridge, MA
11. Ovchinnikov S 1996 Means on ordered sets. Mathematical Social Sciences 32: 39–56
12. Sommer R, Suppes P 1997 Dispensing with the continuum. Journal of Mathematical Psychology 41: 3–10
13. Suck R 1990 Conjointness as a derived property. Journal of Mathematical Psychology 34: 57–80
14. Suck R 1998 A qualitative characterization of the exponential distribution. Journal of Mathematical Psychology 42: 418–31
15. Suck R 2000 Scale type (N, N) and an order based topology induced on the automorphism group. Journal of Mathematical Psychology 44: 582–99
16. Suck R, Getta A 1994 A reaxiomatization of portfolio theory. Journal of Mathematical Psychology 38: 115–27
17. Wakker P 1988 The algebraic versus the topological approach to additive representations. Journal of Mathematical Psychology 32: 421–35
18. Wille R, Wille U 1993 On the controversy over Huntington’s equations: When are such equations meaningful. Mathematical Social Sciences 26: 173–80