Varieties Of Reduction Research Paper

Such dependency claims have been thought to have far-reaching ramifications not just for ontology but also for methodology. For example, the social sciences investigate social phenomena, involving distinctively social entities, properties, facts, and laws. The individualism–holism debate concerns, in the first instance, the status of these items—whether they are anything over and above the totality of individual entities, properties, laws, and facts—but also the methodological autonomy of the associated sciences. (For an even finer-grained analysis which disentangles other conflated but independent components of this debate, see Pettit 1993.) According to Watkins (writing in the 1950s), individualism holds that social institutions ‘do not possess a quasi-divine autonomy’ (in O’Neill 1973, p. 149), and that ‘every complex social situation or event is the result of a particular configuration of individuals, their dispositions, situations, beliefs, and physical resources and environments’ (in O’Neill 1973, p. 168). He argued that, as a consequence, explanations of social phenomena should be couched in terms of the ‘situations, dispositions, and beliefs of individuals’ (in O’Neill 1973, p. 179). His adversary, Mandelbaum, states holism thus: ‘Societal facts are as ultimate as are psychological facts … those concepts which are used to refer to the form or organization of a society cannot be reduced without remainder to concepts which only refer to the thoughts and actions of specific individuals’ (in O’Neill 1973, p. 223).

As Mandelbaum’s claim here illustrates, definability was once the Holy Grail of the reductionist enterprise. Bertrand Russell famously maintained that postulating entities, in contrast to defining (or ‘constructing’) them, ‘has many advantages; they are the same as the advantages of theft over honest toil’ (Russell 1919, p. 71). But just as when the quest for the Holy Grail looked misguided, some more realistic venture might engage a knight’s energies, so when definability failed to capture the interesting dependency claims, philosophers looked elsewhere. And they have discovered a plethora of dependency relations, some of which hold out the promise of prizing apart the methodological and ontological issues, enabling, for example, both the metaphysical strictures of the individualist and the methodological dispositions of the holist to be accommodated.

1. Explicit Definability

Explicit definition is the clearest way of demonstrating that As are nothing over and above Bs, guaranteeing that all truths about As are expressible by talking overtly only about Bs. A full specification of the Bs yields ipso facto a full specification of the As. An explicit definition of A in terms of B₁, …, B_n has the following general form:

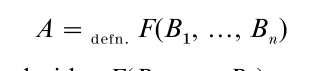
The right-hand side, F(B₁, …, B_n), may involve, in addition to B₁, …, B_n, only certain permissible operations. In the strictest case these are the purely logical connectives (and, not, all, and identity). More liberally one might include the concept of set and set membership, or perhaps the whole apparatus of mathematics. At least as traditionally understood, the definition should be knowable a priori, through pure analysis of the concepts involved, and it should hold by logical necessity.

A striking illustration of the power of definition is logicism, the program to reduce mathematics to logic (Russell 1919). In the nineteenth century, the basic concepts of analysis had been successively defined in terms of the concepts of natural numbers and sets. It began with the elimination of infinitesimals via the definition of a limit. Irrationals were defined as sequences of rationals, and rationals as sets of pairs of natural numbers, leaving the natural numbers alone as primitive, undefined entities. The Russell–Frege definition of natural numbers is remarkable in that it reaches right outside the category of number. Numbers are defined using only the apparatus of logic— including the logic of sets. For example:

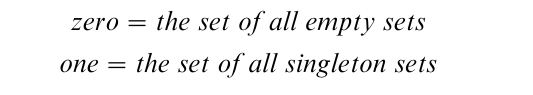
For this to be adequate, truths about numbers must follow from the definitions, together with definitions of the mathematical operations, and the logic of sets. This hope was almost vindicated—but for the discovery of troublesome paradoxes in the foundations of set theory. Despite the paradoxes, the program remained a paradigm of ontological reduction, inspiring much subsequent philosophical activity (Carnap 1928) and providing the framework for most debates about ontological commitments.

2. Reducibility

Definability proved too strong a requirement for typical claims of ontological dependence for reasons involving the constraints that definitions be known a priori and that they hold true by logical necessity.

As is well known, our understanding of the phenomena of heat, codified in thermodynamics, was transformed by the reduction of thermodynamics to statistical mechanics (Nagel 1961, Chap. 11). The reduction involves deducing the laws of thermodynamics from laws of statistical mechanics together with bridge assumptions connecting the concepts of the two domains (temperature and heat with molecule, mass, and motion). For example, the Boyle–Charles law for ideal gases (pressure times volume is proportional to temperature) can be shown to follow from the assumptions of statistical mechanics and the following assumption:

(1) Temperature is mean kinetic energy of component molecules.

Assumption (1) may look like a definition, and is sometimes touted as such, but it is not the result of a priori analysis of its concepts, and it is not logically necessary. (Suppose everything were continuous stuff all the way down and temperature were, say, proportional to density of calorific fluid.) If true, (1) is not logically necessary, and if known, not known a priori.

Some maintain that (1), even if not true by definition or by logical necessity, is nevertheless a matter of identity, vindicating the reductive claim that temperature is nothing but motion of molecules. However, unlike definitional identities, it is a contingent identity, analogous to the contingent identity of the morning star and the evening star (Smart 1959). Analysis of concepts would not yield the fact that the brightest celestial body in the morning sky is identical with the brightest celestial body in the evening sky, and we can easily imagine a world in which they are not. But the morning and evening stars are nevertheless one and the same—Venus. So perhaps (1) states a contingent identity known a posteriori.

The idea that identity (the relation which each entity bears to itself necessarily and to no other thing) could be a contingent matter is still baffling. One way to reduce the baffle is to distinguish between intension (concept) and extension (item singled out). The intension is a certain way of singling out the extension. The extension of both the morning star and the evening star is a chunk of matter, but the intensions are different ways of determining that chunk. The intensions are coextensive in fact but not of necessity.

Property terms also come with an extensional and an intensional component. The extension of black is the class of things that are black. If all black things happened to be chunks of coal, and all chunks of coal happened to be black, then black and coal would be coextensive. They would single out the same class of objects. But is coextensiveness enough for reduction? The two terms are associated with different intensions, they pick out distinct features of the objects, and even if coextensive they would not be coextensive of necessity. Further, we would not be inclined to say that black reduces to coal (or vice versa) just because they were coextensive. So there must be more to reduction of properties than coextensiveness.

Temperature and mean kinetic energy are not properties but magnitudes. Unlike a property, the extension of temperature is not a class of objects. Rather, the temperature of an item can be any one of a number of different possible numerical values—relative to a unit of measure and an origin. The extension of temperature, like mean kinetic energy, thus associates an item with a number. We could construe (1) as the simple claim that the magnitudes temperature and mean kinetic energy are coextensive. However, as the argument concerning black and coal illustrates, a reduction requires a tighter connection. The extensional equivalence reported by (1) has to hold by some kind of necessity (not logical necessity).

A possible world is a complete way the totality of things might be. A state is logically necessary if it holds in all possible worlds. Laws of nature rule out some but not all possibilities (some laws might have been different from what they are in fact) so they are not logically necessary. But what the laws of nature entail involves a kind of necessity—nomological necessity. A state is nomologically necessary if it holds in all worlds in which the actual laws of nature hold. For example, if the theory of relativity is true then in some sense it is impossible for an object to accelerate through the light barrier. This is not just an accidental fact, like the decay of some radium atom, but it is not logically necessary either. It is nomologically necessary.

For (1) to constitute a reduction it must be understood as the claim that temperature is coextensive with mean kinetic energy by nomological necessity. We can now exhibit the difference between definability and reducibility:

A is definable in terms of the Bs, just in case A is coextensive with F(B₁, …, B_n) by logical necessity.

(Or: A is logically equivalent to F(B₁, …, B_n).)

A is reducible to the Bs, just in case A is coextensive with F(B₁, …, B_n) by nomological necessity (in the domain of the Bs).

(Or: A is nomologically equivalent to F(B₁, …, B_n).)

It follows that A is reducible to the Bs if A is nomologically equivalent to something definable in terms of the Bs. Definability entails reducibility (since logical necessity entails nomological necessity) but not vice versa.

Just as (1) transformed our understanding of temperature, our understanding of a mental state like pain may be transformed by the following claim:

(2) Pain is the stimulation of C-fibers in the brain.

For this to be a reductive claim on the model of (1), pain must be nomologically equivalent to C-fiber stimulation. What play the roles here of reducing and reduced theory? The reducing theory would be neurophysiology, and the reduced theory could be our ordinary everyday conception of pain—collections of platitudes like:

Pain is typically brought about by bodily damage, and results in wincing, groaning, and avoidance Behavior.

Such platitudes were central to the Behaviorist hope that pain might be characterized, or defined, in purely behavioral terms (Ryle 1949). When this hope of definability was abandoned the platitudes were central to the functionalist hope that pain could be suitably reduced to physical states of the brain (Lewis 1993, essay 7, Armstrong 1968). Assumption (2), together with a suitably rich scientific theory, might well yield such platitudes. There is a puzzle here to do with the status of the bridging principles like (1) and (2). If we want to reduce the mental to the physical, for example, by exhibiting purely physical (nomological) equivalents of mental features, we would not want to have to acknowledge irreducible laws governing the psychological realm, or irreducible connections between the two realisms. So for reductionism to follow, the laws underpinning nomological equivalents stated in the bridging principles would have to be laws of the lower-level domain—in this case purely physical laws. The puzzle is how purely physical laws could entail principles straddling the two domains—an answer will be presented in Sect. 5.

If analogous reductions were to hold for all mental features then physicalism—the thesis that the mental is nothing over and above the physical—would be vindicated. Undergirding the reduction would be a multitude of nomologically necessary extensional equivalences between mental terms on the one hand and logical products of purely physical terms on the other. A successful reduction would not, of course, entail the elimination of mental entities or of the laws within the mental realm. (The reducibility of thermodynamic laws to statistical mechanics is rather a vindication of the former.) And far from being the denial of systematic and law-like mental–physical connections it is the very affirmation of them—in the form of bridge principles.

3. The Problem Of Networking

For a successful reduction we must have appropriate logical or nomological equivalents. There is, however, an important objection to the existence of such equivalents in two central cases—the relation between the mental and the physical, and the relation between the social and the individual—namely, the heavily networked character of the concepts characteristic of different domains. Mental concepts are heavily networked not just with behavioral and physical concepts but also with other mental concepts. Social concepts are heavily networked not only with each other but also with psychological concepts via those very same social concepts.

Consider pain again. Pain is tied not only to physical inputs and behavioral outputs, but also to other psychological states. Those in pain tend to believe they are in pain, and desire to get out of it. These are platitudes about pain which any reductive account of pain should accommodate. So it looks as though there may be no simple way of giving logical or nomological equivalents of pain in purely physical terms.

The case of social concepts is even more acute. Consider the statement, ‘Jones cashes a check at the bank.’ The predicate involves a social property— making essential use of the social concept of a bank—and the claim itself entails the existence of a bank. According to Mandelbaum, we cannot eliminate the concept bank in explicating the content of this claim. An analysis in terms of psychological states (of Jones, the teller, the bank manager, etc.) would have to include beliefs and desires the contents of which will essentially involve the concept of bank.

… concepts involving the notion of status and role cannot themselves be reduced to a conjunction of statements in which these or other societal concepts do not appear (O’Neill 1973, p. 225).

So here is an obstacle to finding a purely individualistic equivalent of the social property. While Mandelbaum is thinking in terms of definability, a similar argument might be mounted against reducibility.

4. Implicit Definability

The networking problem was solved by an elegant theory of implicit definition, initially discovered by Carnap in the course of his search for a reduction of the theoretical to the observable (Carnap 1966) and fully developed by Lewis into a general reductionist framework (Lewis 1993, essay 6).

Quine famously argued, against positivism, that theoretical terms gain their meaning from being heavily networked with each other and with observable terms only in the context of a rich and testable theory (Quine 1961). Carnap proposed an essentially reductionist account of such terms which nevertheless accommodated this holistic thesis. The essential ingredient was provided by a then little known result of Ramsey (1931). Ramsey showed how a theory about, for example, electrons and protons, T(electron, proton, …) could be stripped of explicit mention of unobservable entities and replaced by a lean purely observational surrogate, its so-called ramsification. Theoretical terms—electron, proton—are first replaced with variables, E, P, (or ‘gaps’) to yield a ‘gappy’ sentence T(E, P, …) which may or may not be true depending on what the gaps are filled with. Now consider the definite claim that the gaps can be indeed truly filled by something or other:

This stripped-down version of the theory entails nothing nontrivial about electrons or protons (because it does not mention them at all), but does entail all the purely observational consequences of the full-blown theory. Since the point of the theory (according to the positivists) is to generate observational consequences, and the ramsification does this without reference to theoretical entities, Ramsey concluded that the theoretical ontology is redundant (Ramsey 1931).

Carnap drew a different lesson. He agreed with Ramsey that the factual component of the theory is delivered by its ramsification, but he noted that for the factual claim to be true there must be some items satisfying the gappy statement T(E, P, …)—for that is exactly what the ramsification says. In that case, we may as well regard those items as the intended extensions of the concepts electron and proton. The whole theory thus serves as a partial constraint on the meanings of its own theoretical terms. It is partial, both because it places no constraints in the case in which the theory is not observationally adequate, and because even when it is there may be a range of legitimate satisfiers of the gappy claim. However, in certain cases we may be lucky and the theory might be strong enough to single out a unique set of satisfiers. In that case we can use the theory to give an explicit definition (Lewis 1993, essay 6).

Something analogous can be sketched for mental properties. We begin with our ordinary everyday collection of platitudes about the mental (‘folk psychology’) in which, as noted, the mental concepts such as pain and desire are heavily networked with each other and with behavioral and physical concepts. Now ramsify this theory, eliminating the mental concepts and replacing them with variables (P for pain and D for desire). The ramsified theory will look something like this: there is a property P typically caused by bodily damage and which causes wincing, and if a something has P it typically bears D to getting rid of P.

This ramsification is stated purely in physicalistic and behavioral terms and might be true of a system which consisted only of physical constituents with purely physical properties. Neurophysiologists might discover that C-fiber stimulation is a feature typically caused by bodily damage and causes wincing; that Cfiber stimulation initiates D-fiber stimulation, which in turn causes C-fiber stimulation-ridding behavior, and so on. Enough of these would support the claim that pain is nomologically equivalent to C-fiber stimulation; the desire to get rid of pain nomologically equivalent to D-fiber stimulation, and so on.

If this is right, then the holistic and networked character of the mental is not itself an insurmountable obstacle to reduction in the case of the mental. Hopefully something similar might be achieved for the social domain. The reduction in the latter case would be to purely individual properties and relations— psychological, behavioral, and physical—which may in turn be reduced to the purely physical.

5. Multiple Realizability

Not long after functionalism had provided this systematic framework for reduction, philosophers began to worry that there may be no appropriate, law-like extensional equivalences in the case of the mind (Putnam 1967, Davidson 1970). Suppose in a typical human being pain is ‘realized’ by C-fiber stimulation, whereas in some untypical humans it is D-fiber stimulation, and in Fido the dog it is E-fiber stimulation. Suppose, further, that there is no end to the number of different states which realize pain in different beings. Suppose in some distant galaxy silicon-based aliens have evolved, or could evolve, with a very different physical structure. Would not they be capable of experiencing pain too? There may be no limit to the ways in which pain can be thus realized in physical beings. So there may be no single, purely physical, nomological equivalent of pain. Pain would not be reducible to the physical.

Or think of the economic institution of cash. Lots of different kinds of stuff in fact play the role of cash, and almost any suitably portable object could play the role of cash given an appropriate combination of beliefs, desires, and conventions. Now reducibility is a transitive relation: if A is reducible to the Bs and the Bs are reducible to the Cs, then A is thereby reducible to the Cs. So if the social is reducible to the physical and the psychological, and the psychological in turn to the physical, then the social is reducible to the physical. But, given that almost any physical item at all could be cash, is it plausible that there be a single, purely physicalistic, nomological equivalent of cash? Hardly.

Does multiple realizability render physicalism and individualism false? Alternatively, is reducibility as characterized necessary for ontological dependence? Suppose every property which realizes pain (or cash) in all nomologically possible circumstances is itself a purely physical property. Would that not be compatible with physicalism? This suggests the possibility of a relation between the mental and the physical weaker than full reducibility but strong enough to vindicate the idea that the mental is nothing over and above the physical.

6. Supervenience

The favored term for the desired relation, one which guarantees determination without entailing reducibility, is supervenience—a term first used to characterize the relation between the moral and the natural.

It is widely held that moral differences are undergirded by natural or nonmoral differences. Suppose Francis of Assisi is good in virtue of kissing a leper with putrefying flesh (Francis of Assisi 1903). Then if Clare kisses an exactly similar leper and she is not good then there must be some nonmoral difference between the two—perhaps, unlike Francis, Clare is suppressing revulsion. Sameness of nonmoral features guarantees sameness of moral features. A difference at the moral level requires a difference at the nonmoral level. The moral supervenes on the nonmoral.

In the social realm, the individualist’s battle cry might be: no difference at the social level without some difference at the individual level. Sameness at the individual level guarantees sameness of social features. That kind of supervenience claim seems eminently reasonable, one which even a holist might be embarrassed to deny. If Jones cashes a check in situation A but not in situation B, then there must be some difference at the individual level between the two situations—either between Jones in A and B, or between some other individuals in A and B. Kim generalizes the supervenience condition thus:

One family of properties is ‘supervenient’ upon another family of properties in the sense that two things alike with respect to the second must be alike with respect to the first (Kim 1978, p. 149).

So stated the principle is open to interpretation. The necessity involved (‘must be alike’) may be logical or nomological. Some supervenience claims—like the supervenience of the moral on the non-moral—are a matter of logical necessity (although see Oddie 1991). Other supervenience claims are a contingent affair. Most physicalists think that the supervenience of the mental on the physical is a contingent matter—for we can imagine worlds consisting of unembodied minds differing in their mental attributes but (lacking bodies) being physically indistinguishable. The supervenience of the social on the individual is disputed—some hold it to be a logical affair (Currie 1984) others a contingent affair (Pettit 1993).

Kim’s statement of the supervenience principle requires individual by individual comparison: any two B-indiscernible individuals must be A-indiscernible. It has therefore been dubbed a kind of local supervenience. This may be too stringent for characterizing the supervenience of the social on the individual (Currie 1984) and even for the supervenience of the mental on the physical (Burge 1979). In both cases, it is claimed, the supervening properties involve not only the local properties of the individual, but the relations of the individual to its environment as well as to other individuals. (Whether Clinton is the President depends not just on Clinton’s psychological and physical state but on psychological and physical states nationwide. Whether Clinton thinks that that woman is sexy requires a real woman, not just an hallucinated woman, to be there.) Furthermore, in the social case, some of the supervening entities (First Bank of Boulder, the Stock Market, France) are in any case of a different logical type from the individuals on which they are claimed to supervene, so we need to compare more than just the social properties of individuals. Finally, a number of arguments have shown that, given reasonable assumptions, local supervenience of the logical variety entails definability, and local supervenience of the nomological variety entails reducibility (Kim 1978, 1989, Bacon 1986, Oddie 1991), thereby failing the nonreductionist desideratum.

In order to avoid these problems global supervenience has been put forward as the salient relation. Call two worlds B-indiscernible if the Bs have the same extensions in both (that is, the Bs are identically distributed in the two worlds). Then A globally supervenes on the Bs if any two (nomologically) possible worlds which are B-indiscernible (the Bs have the same extensions in both) are also A-indiscernible (A has the same extension in both). This principle is a desideratum of any concept of determination, and so it is the weakest relation that might serve the supervenience theorist’s purposes.

Definability entails global supervenience of both logical and nomological varieties, and reducibility entails global supervenience of the nomological variety. Since global supervenience is the weakest principle guaranteeing determination, the crucial remaining question is whether it avoids reducibility. To illustrate this possibility let us define a very simple, albeit artificial, property, G:

(3) G = being both poor and identical either to Clare or to Francis.

Only Clare and Francis can have G, and they have it just in case they are poor. So any two worlds which are identical in the distribution of poverty will be identical in the distribution of G. That is to say, G globally supervenes on poverty.

Is G reducible to poverty? Let us suppose all four logically possible distributions of G are also nomologically possible. Is G nomologically equivalent to something definable solely in terms of poverty? (3) is not such a definition. On the right-hand side, in addition to poor, the logical connectives (and and/or) and the identity relation, we have reference to two individuals. Identity, like the logical connectives, is typically counted part of the logical apparatus and so a permissible component of a definition. But the individuals Francis and Clare are not. If we disallow direct reference to Francis and Clare, or to any entity like the property of being identical to either Francis or Clare which could perform the same logical role, then G cannot be defined in terms of poverty alone. Given this, there is no nomological equivalent of G in terms of poverty. G is neither definable in terms of, nor reducible to, poverty.

Like nearly every philosophical argument, this one involves some disputed assumptions, but if it is right then it illustrates the possibility of global supervenience without reducibility (a substantial simplification of the point first made by Hellman and Thompson (1975)).

7. Conclusion

If global supervenience yields determination without reducibility then this is good news indeed for nonreductive physicalists and non-reductive individualists. The determination component articulates a clear sense in which the social and the mental are nothing over and above the physical. In creating the actual world God would not first have to create physical stuff and the laws governing it, then add a whole layer of extra mental entities, properties, and laws, and finish it up with social entities and laws. The physical by itself would suffice, guaranteeing its mental and social superstructure. The nonreductive component, how-ever, would guarantee that mental and social concepts would still be essential for discourse and theorizing. The social sciences could enjoy methodological autonomy without having to apologize for a bloated ontology.

Bibliography:

1. Armstrong D M 1968 A Materialist Theory of the Mind. Routledge, London
2. Bacon J 1986 Supervenience, necessary coextension, and reducibility. Philosophical Studies 49: 163–76
3. Burge T 1979 Individualism and the mental. Midwest Studies in Philosophy 4: 73–121
4. Carnap R 1928 Der Logische Aufbau der Welt. Weltkreisverlag, Berlin
5. Carnap R Philosophical Foundations of Physics. Basic Books, New York
6. Currie G 1984 Individualism and global supervenience. British Journal for the Philosophy of Science 35: 345–58
7. Davidson D 1970 Mental events. In: Foster L, Swanson J W (eds.) Experience and Theory. University of Massachusetts Press, Amherst, MA, pp. 79–101
8. Francis of Assisi St 1903 The Little Flowers of Saint Francis [trans. Arnold T W]. Dent, London
9. Hellman G, Thompson F 1975 Physicalism: ontology, determination, reduction. Journal of Philosophy 72: 551–64
10. Kim J 1978 Supervenience and nomological incommensurables. American Philosophical Quarterly 15: 149–56
11. Kim J 1989 The myth of non-reductive materialism. Proceedings and Addresses of the American Philosophical Association 63: 31–47
12. Lewis D 1993 Philosophical Papers. Oxford University Press, New York, Vol. 1
13. Nagel E 1961 The Structure of Science. Harcourt, Brace & World, New York
14. Oddie G 1991 Supervenience, goodness, and higher-order universals. Australasian Journal of Philosophy 69: 20–47
15. Oddie G, Tichy P 1990 Resplicing properties in the supervenience base. Philosophical Studies 58: 259–69
16. O’Neill J 1973 Modes of Individualism and Collectivism. Heinemann Educational, London
17. Pettit P 1993 The Common Mind. Oxford University Press, New York
18. Putnam H 1967 Psychological predicates. In: Capitan W H, Merrill D D (eds.) Art, Mind and Religion. Pittsburgh University Press, Pittsburgh, PA, pp. 37–48
19. Quine W V O 1961 Two dogmas of empiricism. From a Logical Point of View. Harvard University Press, Cambridge, MA
20. Ramsey F P 1931 The Foundations of Mathematics. Kegan Paul Tranch, Trubner, London
21. Russell B 1919 Introduction to Mathematical Philosophy. Macmillan, New York
22. Ryle G 1949 The Concept of Mind. Barnes & Noble, New York
23. Smart J J C 1959 Sensations and brain processes. Philosophical Review 68: 141–56