Numerical Methods In Historical Linguistics Research Paper

2. Early Methods

The earliest precursor to a numerical method in historical linguistics is a statement made by Robert Gordon Latham (1850, p. 565, see also Hewes in Hymes 1960, p. 338): ‘the average rate at which languages change is capable of being approximated’ and ‘the maximum difference, at a given period, between two or more languages is also capable of being approximated.’ He never pursued this, and the next milestone in the development of numerical methods in historical linguistics was a statement by Sapir (1916, p. 76): ‘The greater the degree of linguistic differentiation within a stock the greater is the period of time that must be assumed for the development of such differentiation.’ Sapir’s influence on later linguists was great, so even though he himself never followed this statement up by taking the basic steps of quantifying linguistic differentiation or rate of change, this can be seen as the genesis of the most widely known numerical method in historical linguistics, that of Swadesh (1950, and see below).

The first explicit numerical treatment of genetic proximity of languages was Kroeber and Chretien (1937), following a method created by two anthropologists, Jan Czekanowski (1928) and Stanislaw Klimek (1935), for use in physical anthropology and ethnography. For each pair of languages, on a list of N features, calculate a (number of features shared by both languages), b (number of features in the first language but not the second), c (number of features in the second language but not the first), and d (number of features in neither language). This produces a 2×2 contingency table, a wellstudied mathematical entity enabling various forms of analysis. In particular, the quantity Nr², where r=(ad-bc)/√(a+b)(c+d )(a+c)(b+d ), is χ² (one degree of freedom), enabling one to test the statistical significance of the relationship between the two languages. The values of r for all pairs of languages under consideration can become the input to various methods (e.g., hierarchical cluster analysis) for family tree reconstruction. The method is simple but not unproblematic (e.g., construction of the feature-list, difficulties with non-independence of features, interpretation of correlations especially if negative). (For fuller treatment and commentary, see Embleton 1986.)

The second numerical method in historical linguistics is Ross’s root-retention model (1950). For N features and m languages, construct an N×m table in which a cell has a cross if that language exhibits that feature. The question of relationship of languages can then be recast as whether or not the crosses are distributed randomly in the table. For each pair of languages, calculate n₁ (number of features found in the first language is represented by the number of crosses in the first column), n₂ (number of features found in the second language is represented by the number of crosses in the second column), and r (number of features shared by both languages is represented by the number of rows with a cross in both columns). Then the probability for that pair of languages of obtaining the shared number of crosses or more is

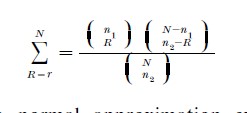
for which a normal approximation exists. These probabilities can be tested for significance, and could become the input for various family tree reconstruction methods. Interestingly, Ross’s method can be shown to be mathematically equivalent under certain conditions to Kroeber and Chretien’s, and thus subject to the same problems. (For fuller treatment and commentary on this and the method in general, see Embleton 1986.) Although certain elements of these models recur today, both have largely been abandoned, although the problems encountered and lessons learned remain relevant.

Historically, the next method to evolve was Swadesh’s, but given its centrality to the field and ongoing relevance, I will deal with that in a separate section. A final numerical method to consider is that of counterindications originated by Gleason (1959), later rediscovered by others. All topologically possible family trees for the languages in question are constructed, each is evaluated for how well it fits against a fixed list of features (every time the tree does not fit the distribution of that feature, a counterindication is recorded), and the tree with the best score (even if not perfect) is chosen. This method is difficult to implement for two reasons. Even with modern high-speed computing and sophisticated algorithms, the number of topologically possible trees for even a moderately-sized language family quickly becomes unworkably large. The method is also highly vulnerable to the effect of borrowing across languages. A variant of Gleason’s method, relying on hierarchical clustering and attempting to estimate branch lengths (i.e., used glottochronologically) is shown in Embleton (1986), along with fuller discussion of the method itself. Taylor et al. (2000), using recent advances and sophisticated techniques from computer science and biological cladistics, are developing a character-based (rather than distance-based) method for family-tree reconstruction with some similarities to Gleason’s method. Despite difficulties with dealing with borrowing in realistic amounts, such methods are promising partly because they closely parallel the cognitive processes of skilled practitioners of traditional comparative-historical reconstruction techniques, while being more objective and simultaneously handling vast amounts of data.

3. Swadesh

By far the best known numerical method in historical linguistics is that introduced by Swadesh (e.g., 1950), actualizing Sapir’s statement by regarding lexical replacement as analogous to radioactive decay. As with carbon-14 dating, dates could then be provided for branching points in the tree (glottochronology). Take a list of N meanings of supposed basic core vocabulary, found universally in all cultures, expressing basic noncultural concepts, expected to be more resistant to change and borrowing than other vocabulary items. Such a list, now known as a Swadesh list, contains such items as lower numerals, simple kinship terms, body parts, topographical terms, widespread flora and fauna, pronouns (personal, demonstrative, interrogative), verbs denoting basic actions, and naturally occuring noncultural phenomena. Assuming a constant rate of replacement, R, for words representing meanings on this list, one can calculate the time elapsed (time depth) since any pair of languages split using the formula

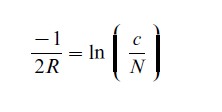
where c is the number of cognates on the Swadesh-list between the two languages compared. By calculating time depths for all pairs of languages under consideration, we can construct a family tree with dates.

Swadesh’s method was greeted with widespread enthusiasm and widely applied in the late 1950s, 1960s, and early 1970s, almost with a sense of euphoria about finally having an exact tool for obtaining insights into hitherto unknowable linguistic prehistory. The debate over Swadesh’s method quickly became emotional, but regardless of the researcher’s subjectivity, a common core of problems can be identified, sometimes with potential solutions.

Difficulties with particular meanings on the Swadesh-list.

(a) Some meanings cannot be translated into the target language. This is fairly rare, and best treated as missing data, reducing N accordingly.

(b) Sometimes there are multiple possible translations in the target language for a meaning on the list. Different researchers might make different but equally valid choices from the range of possibilities (‘multiple synonymy’). Solutions include always counting only the most frequent possible translation, choosing at random, always choosing to maximize the cognate count, always choosing to minimize the cognate count, or various fractional scoring systems.

Difficulties with cognacy judgments (remember one is not necessarily dealing with languages where the history, and hence cognacy are well known).

(a) Due to accumulated sound change, cognates may not be recognizable, causing us to overestimate time depth.

(b) Chance similarities may be wrongly interpreted as cognates, causing us to underestimate time depth. In practice, one might hope that this and the preceding cancel out.

(c) Sometimes only one part of a word is cognate to a word in another language (‘partial cognation’); how should one score this? Solutions include always counting this as positive, always counting this as negative, or various fractional scoring systems.

Problems with the universality of R, which was shown to vary over time, between languages, and according to meaning. R had been estimated from languages with written historical records as about 14 percent per millennium for the standard 100-word Swadesh-list and about 19 percent per millennium for the standard 200-word Swadesh-list. Not only might the very fact that these languages are written bias the rate (one might expect less replacement in a language with a lengthy written history), but 11 of the 13 pairs used to establish the rate were Indo-European (representing only three of its branches).

Problems with the family tree (Stammbaum) model, generally centering around the splits not being clean (thus giving any precise date is artificial and meaningless). Languages are often in close physical proximity even after they split, mutually influencing one another; tendencies in the two languages predating the split may come to fruition only afterwards. Both these interfere with the model, but are more properly problems with the family tree model, and Swadesh’s adoption of it, rather than problems with Swadesh’s method itself.

Borrowings between languages (related or unrelated) can alter replacement rates quite substantially. For some languages, even the Swadesh-list contains a high amount of borrowed vocabulary.

For various reasons (see Embleton 1986 and elsewhere), the use of Swadesh-style lexicostatistics and glottochronology waned by the mid-1970s, although applications lingered on in several language areas, and the methods continued to be refined by applied mathematicians.

4. Sankoff

Most refinements introduced by applied mathematicians involved adding further parameters to the basic Swadesh model. For example, parameters were added to account for drift and for ‘chance recurrent cognation’ (i.e., when a word was replaced twice, such that the original word was restored), replacement rates were allowed to vary from meaning to meaning, a very crude allowance was made for borrowing, and there was talk of allowing the rates to vary from language to language and from time to time. (Further details, along with some models, can be found in Embleton 1986.) Some of these are useful refinements (e.g., allowing replacement and borrowing rates to vary over time, between languages, and between meanings), but these are very much a mathematician’s way of solving the problem, producing quite elegant solutions. But in the real world in which the linguist works, all those parameters have to be estimated—and this is surprisingly difficult even for well studied languages for which we actually have both long and extensive written records. It is also the case that an extraordinary amount of data is required to estimate so many parameters, and this is most often simply impossible. So these elegant theoretical solutions have very little practical import.

However, the single most important development was the incorporation of a geographical dimension into the family tree, thus allowing for borrowing to be largely dealt with. The basic insight here is due to Sankoff (1972), with correction and further refinement by Embleton (see 1986 for the most comprehensive treatment). The resulting set of differential equations required to reconstruct the tree and estimate the branch lengths is complicated, reflecting the increased power of the method (equations are given in Embleton 1986 and elsewhere). The parameters required all have some reasonable chance of being estimated, even for lesser studied families; these are a similarity measure for each language pair, replacement rates for each language, borrowing rates between each language pair (not necessarily symmetric), and knowledge of which languages are in contact with one another.

5. Starostin

Largely independently of the work described above, research on numerical methods in historical linguistics was proceeding in the Soviet Union (later Russia, still later ‘in diaspora’). Unlike the impetus for Swadesh’s work, which was largely to aid in providing histories and trees for relatively little studied language families (e.g., Amerindian), much of this work gained its impetus from questions of more distant linguistic relationship. This had its effect on the development of the methods, because it was crucial that the methods be able to produce useful results even at much greater time depths, where Swadesh’s method typically has difficulty distinguishing the signal (cognacy, true genetic relationship) from the noise (chance resemblance, contact relationship).

Historically the first advance here was due to Dolgopolsky (1986), who capitalized on the fact that different meanings change at different rates. He compiled a list of the 15 most stable meanings, based on examination of 140 languages. One can then calculate the probability of fortuitous coincidence of the words representing those 15 most stable meanings for any language pair; if the probability is significantly less than that expected by mere chance, this can be taken as evidence of relationship. This method is most striking in its extreme simplicity, but can also be related to some more complex and ongoing work, largely carried out in eastern Europe, founded on the observation that several characteristics of a word (e.g., length, number of meanings, age) are intercorrelated with its frequency. Words of more recent origin tend to be less frequent, longer, and have fewer meanings, whereas older words tend to be more frequent, shorter, and have more meanings. The age-frequency relationship in particular is being extensively researched, as there may be a small hard core of ancient short vocabulary which may reveal distant relationships, and may even be able to be harnessed into a lexicostatistical or even glottochronological method.

Another advance has been made by Sergei Starostin, with work first published in the 1980s and continuing to the present, known as root glottochronology or etymostatistics (see Starostin 1999). Compared to standard Swadesh-style glottochronology, the main innovation is the observation that while glottochronology regards any change (however small) in a word’s meaning as a loss of that word from that meaning, root glottochronology does not. Thus while standard glottochronology sees English dog and German Hund in the meaning ‘dog’ as noncognate, root glottochronology notices the existence of the English word hound; this more conservative approach to the maintenance of a language’s root stock enables one to work better at greater time depths. Starostin’s method also gives more accurate results for known cases where the time depths are more shallow (standard glottochronology tends to give dates which are too recent). Root glottochronology takes a text, containing a given set of words in the parent language, and then measures the number of these words still extant (in any derivative, with any semantic shift) in the daughter language. It proceeds only with detailed comparativehistorical and etymological analysis (eliminating lookalikes and loans), and also can be repeated for more than one text (hence a different set of words), giving greater precision and potentially some estimate of error (see Starostin 1999 for formulas and more detailed explanation).

6. Ringe

Various linguists have used probabilistic methods to assess similarity between vocabularies of two different languages, usually focusing on phonological similarities (an early example is Ross 1950). The basic question is whether the observed degree of similarity between the two vocabularies is greater than what could be expected based on chance. Although the problem is conceptually simple, it quickly becomes mathematically intractable even between just two languages, as one has to wrestle with different phoneme distributions, different phoneme frequencies, how to measure phonetic distance between different phone(me)s, different phonotactic structures, and lengths of roots, quite apart from the questions (familiar from glottochronology) of how much semantic latitude to allow between the words compared. The most recent and sophisticated treatment of this problem is by Ringe (e.g., 1998 and references therein), who attempts to account for many of the above issues, albeit with simplifying assumptions. This research remains active, yet without consensus as to its utility, partly because of the degree of the simplifying assumptions, but also partly because it has mostly been applied in the realm of long-distance relationships, where the emotions over the results can sometimes cloud the objectivity with which the method is viewed.

7. Future Directions

Research in numerical methods in historical linguistics is gradually reentering the mainstream after several decades on the sidelines. The most active areas of current research are improvements to the basic Swadesh model, exploration of the age–frequency relationship, root glottochronology, computer-implemented tree reconstruction using methods borrowed from biological cladistics, and Ringe’s probabilistic methods. The degree of mathematical, statistical, or computational expertise required is extremely high, which is likely to prevent the majority of historical linguists from ever mastering the methods, and consequently render them unable to do more than use results produced by others or participate in research teams where others control the methods. There seems to be a growing realization, however, that numerical methods, while not providing any magic solutions to any long-standing problems, can make a useful contribution as one of the tools that we use to explore our linguistic history and prehistory.

Bibliography:

1. Czekanowski J 1928 Na Marginesie Recenzji P. K. Moszynskiego o Ksiazce: Wstep do Historji Slowian. Lud, Series II, Vol. 7. Reprint Lwow, 1928
2. Dolgopolsky A 1986 A probabilistic hypothesis concerning the oldest relationships among the language families in northern Eurasia. In: Shevoroshkin V, Markey T (eds.) Typology, Relationship and Time: A Collection of Papers on Language Change and Relationship. Karoma, Ann Arbor, MI, pp. 28–50
3. Embleton S M 1986 Statistics in Historical Linguistics. (Quantitative Linguistics, Vol. 30). Brockmeyer, Bochum, Germany
4. Gleason H A Jr 1959 Counting and calculating for historical reconstruction. Anthropological Linguistics 1: 22–32
5. Hymes D H 1960 Lexicostatistics so far. Current Anthropology 1: 3–44; 338–45
6. Klimek S 1935 The structure of California Indian culture, culture element distributions: 1. University of California Publications in American archaeology and Ethnology 37: 1–70
7. Kroeber A L, Chretien C D 1937 Quantitative classification of Indo-European languages. Language 13: 83–103
8. Latham R G 1850 The Natural History of the Varieties of Man. Van Voorst, London
9. Ringe D R Jr 1998 Probabilistic evidence for Indo-Uralic. In: Salmons J C, Joseph B D (eds.) Nostratic: Sifting the E idence. Benjamins, Amsterdam, pp. 153–97
10. Ross A S C 1950 Philological probability problems. Journal of the Royal Statistical Society B 12: 19–59
11. Sankoff D 1972 Reconstructing the history and geography of an evolutionary tree. American Mathematical Monthly 79: 596– 603
12. Sapir E 1916 Time Perspective in Aboriginal American Culture (Memoir 90, Anthropological Series, Vol. 13). Government Printing Bureau, Ottawa, Canada
13. Starostin S 1999 Comparative-historical linguistics and lexicostatistics. In: Renfrew C, McMahon A, Trask L (eds.) Time Depth in Historical Linguistics. McDonald Institute for Archaeological Research, Cambridge, UK, Vol. 2, pp. 377–413
14. Swadesh M 1950 Salish internal relationships. International Journal of American Linguistics 16: 157–67
15. Taylor A, Warnow T, Ringe D 2000 Character-based reconstruction of a linguistic cladogram. In: Smith J C, Bentley D (eds.) Historical Linguistics 1995. Selected Papers from the 12th International Conference on Historical Linguistics, Manchester, August 1995, Vol. 1, General Issues and Non-Germanic Languages. Benjamins, Amsterdam, pp. 393–408