Numeral Systems Research Paper

The spoken and written-out forms of numerals differ in various ways from the Arabic notation. There may be a difference in base number; thus French expresses 80 as quatreingts, literally 4 20s. There may also be a difference in the order of constituent elements; thus German expresses 64 as ierundsechzig, literally 4 + 60. The scientific notation is compact, having no explicit representation of addition and multiplication, and relying on the place-value convention to indicate powers of the base 10. But natural language numeral systems are not as compact, having explicit representations of the addition operation (e.g., and in two hundred and sixty), and explicitly naming the powers of the base number (e.g., in English with the suffix -ty and words such as hundred and million). As such vernacular forms precede the scientific notation (both in the history of a language and in the order of acquisition by individuals), it is the spoken and written-out forms of numerals, and their mapping onto numbers, that concern us here.

Some languages have no numerals:

The one obvious gap in Australian vocabularies is the lack of any system of numbers. It is usually said that there are only numbers ‘one,’ ‘two,’ ‘several’ and ‘many’; some languages appear also to have ‘three,’ although this is frequently a compound form. Kenneth Hale has suggested that these forms are not numerals in the strict sense, but are rather indefinite determiners, like English a and some (Dixon 1980, pp. 107–8).

In languages with a numeral system, forms for expressing positive whole numbers are in frequent use in everyday life, whereas forms for expressing more technical concepts, such as negative numbers and fractions, either do not exist or are restricted to technical discourse. Subsidiary systems, such as systems for naming dates, clock times, amounts of money, weights and measures, or telephone numbers, are derivative of the basic numeral system of a language, and are of less interest to the linguist, often being of recent invention, in some sense artificial, and following idiosyncratic rules characteristic only of themselves.

Numeral systems, though well integrated into their host languages, are nevertheless somewhat atypical of language subsystems as a whole. Numerals are the only expressions for which a conventional sequence exists. Thus there is an agreed answer to the question, ‘What comes after sixteen?’ But there is no such agreed sequence, in any language, for, say, the adjectives and adjectival phrases of the language. Obviously this sequencing is due to the especially clear semantic domain of numerals, the sequence of natural numbers. Numeral systems, beyond the most rudimentary, are also atypical in that they are usually explicitly taught. Children are drilled in reciting a conventional sequence of numerals, whereas almost every other part of the core grammar of a language is acquired without explicit teaching or drilling. This might be grounds for arguing that numerals themselves are to some extent artificial and not part of the core grammar of any natural language. But if we take the notion of what belongs to a language broadly, there can be no doubt that a language’s numeral system is a proper part of it; a section on the numeral system of a language is incorporated into any decent reference grammar.

1. Numerals And Grammatical Number

Grammarians use the term ‘(grammatical) number’ for the singular plural distinction marked on nouns in most languages, and supplemented in some languages by categories such as dual, and even trial. Grammatical number tends to be indicated in the morphology of nouns (e.g., by an affix), whereas numerals are distinct words or phrases. Grammatical number has a loose relationship with numeral expressions in a language. One might expect that in any language the numeral expressing 1 would accompany a singular noun, the numeral expressing 2 would accompany a plural noun (or a dual noun if the language has duals), and any other numeral would be accompanied by a plural noun. But such a neat pattern is not universal. In Hungarian, for example, a noun following any numeral, for whatever number, is grammatically singular; the plural form of a noun is used only in the absence of any preceding numeral expression. In (Egyptian) Arabic, the situation is more complex, with a singular noun accompanying the form for 1, a dual noun going with the form for 2, a plural noun with forms for the numbers 3–10, and a singular noun with forms for 11 upwards. Examples are given below.

ENGLISH    HUNGARIAN          ARABIC

‘minute’        perc     daqiiqa

‘minutes’      percek daqaayiq

‘one minute’             egy perc          daqiiqa waqda

‘two minutes’           ket perc           (itneen) daqiiqteen

‘three minutes’         harom perc     talat daqaayiq

‘ten minutes’            tiz perc            ashar daqaayiq

‘eleven minutes’      tizenegy perc qidaashar daqiiqa

2. Simple Lexical Numerals

Cardinal numeral words are shaped and distributed like adjectives or nouns. Across languages, the lower-valued numeral words (typically up to about the range 2–4) tend to behave clearly like adjectives, and the higher-valued numeral words (especially those used as multiplicative bases, such as hundred and million) behave like nouns. Indeed, there is an example in the table above, in which the Arabic numeral for 1, waaqid, follows its noun, as adjectives do in Arabic, while the other numeral words (for 2, 3, 10, 11, 20) precede their noun, unlike adjectives. (See Corbett (1978a, 1978b) for details.)

In several other respects, the lower-valued numerals, up to about 2–4, behave differently from other numeral words. In some languages, there are different gender forms for just the first few numerals. Thus in Welsh there are masculine /feminine pairs dau/dwy ( = 2), tri/tair ( = 3), and pedwar/pedair ( = 4), but only one form for other numerals. In some case-marking languages, numerals for values up to about 2–4 impose a special case (e.g., Genitive, as in Russian) on a following noun (See Hurford (2000) for examples).

Ordinal numerals (e.g., first, second, third,… twentieth,…), where they exist, are adjectives derived from cardinal numerals. The lower-valued ordinals (again typically up to about the range 2–4) tend to be formed suppletively, without any obvious morphological connection to the corresponding cardinal numeral. Thus first is not formed from one, whereas fourth is formed by suffixing -th to four (see Hurford (in press) for tables of such examples from a range of languages).

3. From Lexicon To Syntax

In some languages, the simple lexical numerals stop at 2, and higher values are expressed by syntactic combinations. An example is given here from a Queensland, Australia language cited in Tylor (1891, p. 243)

(a) ganar

(b) burla

(c) burla-ganar

(d) burla-burla

Other languages make the break into syntax after 3, 4, and 5, and most languages have simple numeral words for values up to 10, and then resort to syntactic combinations. After 10, almost without exception in any language, the only values for which there are morphologically simple words are those used as multiplicative bases, such as 20, 100, 1,000, and so on. (English eleven is an exception, but it is historically derived from a more complex form; Russian sorok (= 40) is a genuine exception. Another source of possible exceptions is the bodypart numeration practices found in some parts of Papua New Guinea. In such practices, parts of the body are touched in sequence as a way of recording or communicating numbers, typically starting with the left little finger, moving through the left digits, up the wrist, forearm, elbow, upper arm, shoulder, neck, head, and down to the right little finger. Thus, bodypart words can be said to have secondary numeral meanings (see Saxe (1981) for details).

4. Basic Syntax Of Numerals

(The material in this section is set out in much greater detail in Hurford (1975).) With remarkable uniformity, the basic form of most syntactically complex numerals in most languages can be generated from a universal schema of just two simple phrase structure rules

Here, ‘NUM’ represents the category Numeral itself, the set of possible numeral expressions in a language; ‘DIGIT’ represents any single numeral word up to the value of the base number (e.g., English one, two,…, nine); and ‘M’ represents a category of mainly nounlike numeral forms used as multiplicational bases (e.g., English -ty, thousand, and billion). The curly brackets in the rules enclose alternatives; thus a numeral may be either a DIGIT (e.g. eight) or a so-called NUMPHRASE (numeral phrase) followed optionally by another numeral (e.g., eight hundred or eight hundred and eight). If a numeral has two immediate constituents (i.e., is not just a single word) the value of the whole is calculated by adding the values of the constituents; thus sixty four means 60 4. If a numeral phrase (as distinct from a numeral) has two immediate constituents the value of the whole is calculated by multiplying the values of the constituents; thus two hundred means 2 × 100.

4.1 Language-Specific Idiosyncrasies

Two sorts of reservation must be made about the claim for the universality of the two basic phrase structure rules presented above. One sort of reservation is a set of language-specific modifications, made on a case-bycase basis for each separate language, essentially dealing with the ways in which the particular language’s irregularities deviate from the universal pattern embodied in the two rules. These idiosyncrasies typically affect the lower-valued expressions (up to about 20, but sometimes higher) only. For instance, the rules, if given an English lexicon, besides generating the regular numeral phrases sixty, seventy, ninety, would also generate *twoty, which needs to be changed to twenty, and *onety, which needs to be changed to ten. The rules above order a numeral phrase before any accompanying numeral, which could be a digit-word, thus generating, correctly for English, for example, seventy two, but incorrectly for German, for example, funfzig drei. Languages which place summands in a lower-before-higher order require a rule (obligatory or optional, as the case may be) reordering the constituents of a numeral. Languages also typically augment the universal rule schema above with their own idiosyncratic rules inserting particles (e.g., and, et, und) denoting addition and, less often, multiplication.

It may be objected that the above forces the numerals of all languages into a Procrustean bed, distorting the true picture in individual languages. Such an objection turns out, on detailed study of individual languages, to be misplaced. Even in the numeral system of just one language, there is usually an indication of a regular underlying system, captured by the rule schema above, to which most of the numeral expressions in the language, including all of the higher-valued ones, conform. Using a handful of idiosyncratic statements to capture irregularities is in fact more economical than postulating a nonuniversal underlying scheme for any particular language.

4.2 The Packing Strategy

The second necessary reservation to the universal rule schema above involves a way of constraining the massive overgeneration resulting from the recursive use of the category NUM in the rules. Without further constraint, these rules would generate (given an English lexicon) such non-existent forms as the following: *sixty ten; *eighty hundred; *two hundred, two hundred, two-hundred; *three million thousand hundred.

The universal rule schema generates hierarchically structured strings, which can be represented in tree diagrams such as in Fig. 1. These examples go in semantically equivalent pairs, as can be determined by adding the values of constituents of a NUM and multiplying the values of constituents of a NUMPHRASE. The first pair both mean 3,200, and the second pair both mean 400,000,000. But only one member of each pair, the left-hand structure, is well-formed. With strikingly few exceptions across all languages, ill-formed numeral structures generated by the universal rule schema can be eliminated by a universal principle known as the Packing Strategy, stated informally below.

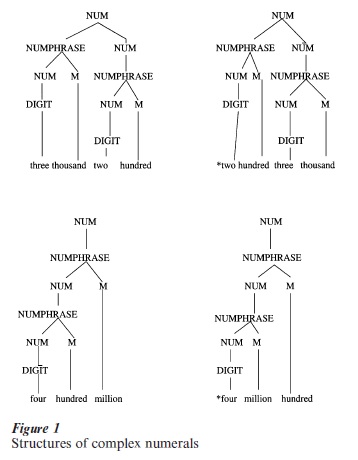
Packing Strategy: within any part of a numeral structure, the sister of a NUM must have the highest possible value.

Another way of stating this is: in a numeral structure, if the sister of a NUM is not the highest valued well-formed structure of its category (equal to or lower in value than the value of the whole structure) generated by the universal schema together with the lexicon of the particular language, the whole structure is ill-formed.

Thus, *two hundred three thousand above is characterized as ill-formed because of the existence of a well-formed NUMPHRASE three thousand which could be the sister of the next-to-top NUM (3,000< 3,200), and which has a value greater than that of the actual NUMPHRASE sister of the next-to-top NUM (3,000 > 200). Similarly, *four million hundred above is characterized as ill-formed because of the existence of a well-formed M million which could be the sister of the next-to-top NUM (l,000,000 < 400,000,000), and which has a value greater than that of the actual M sister of the next-to-top NUM (l,000,000 > 100).

The Packing Strategy works in coordination with the lexicons and other rules of particular languages. Beside the kinds of examples just given, it can be applied to explain some language-specific idiosyncrasies, such as the fact that in French 70 is expressed as soixante-dix ( = 60 + 10), and not as 50 + 20, or 40 + 30, for example. The Packing Strategy can also be used to explain the actual sets of Ms (base words) found in numeral systems. In English, there are Ms with values of 10, 10²(hundred), 10³ ( thousand), (10³)²(million), (10³)³(billion), and (10³)⁴(trillion ). In Chinese there are Ms with values of 10, 10², 10³, 10⁴, (10⁴)², and (10⁴)³ . If one posits internal hierarchical structure for these lexical items, with exponentiation as the relevant arithmetical operator, the existence of such smoothly regular sequences of Ms can be predicted by means of the Packing Strategy.

The Packing Strategy is an unusually powerful generalization across languages. It is not without exceptions. The Packing Strategy predicts incorrectly, for instance, that English expressions such as twenty three hundred would be ill-formed, with two thousand three hundred being the only well-formed expression for 2,300. It is also falsified as an exceptionless generalization by the series of multiplicative bases found in Indian languages, exemplified here from Tamil: 10 paththu, 10² nuru, l0³ayiram, l0⁵laksham, l0⁷ kodi (see Hurford (1975) for more fully argued details of the universal phrase structure rule schema for numerals and the Packing Strategy).

5. Linguistic Discontinuity

The mathematical number series, as defined by Peano, is smoothly continuous from zero to infinity, admitting of no discontinuities. The jump from 1 to 2 is of exactly the same nature as the jump from 2,001 to 2,002. But the sequences of numerals in natural languages show several discontinuities, and all at around the same points. These discontinuity points are typically:

(a) around three, before which lexical numerals show various irregularities, for example, suppletive ordinals, agreement in gender, unusual case government, as mentioned above; psychologically, three is about the limit of subitization (instant number judgement without counting);

(b) after 10, at which point the first syntactically complex numerals typically appear, using addition;

(c) around 20, at the point when the first multiplicative expressions are used, which often coincides with a switch in the way addition is expressed (e.g., English DIGIT + -teen switches to DIGIT-ty DIGIT);

(d) (less often) at a point associated with some higher base number, such as 100 or 1,000, when different detailed rules may begin to apply (e.g., German switches from lower-plus-higher to higher-plus-lower order of summands)

Such linguistic discontinuity suggests a system growing by stages over time, with periods of stasis between each stage. The discontinuities are historical growth marks, like the rings in a tree trunk.

6. Some Idiosyncratic Systems

Linguistics is interested in discovering and explaining both the universal pattern to which all languages are cut and the range of variation within that pattern. Some linguists concentrate more on the universals, some more on variety and idiosyncrasy . The numeral systems of many languages are strikingly similar, but in this section a few examples will be given from unusual systems.

Not many numeral systems use subtraction, but the traditional Yoruba system uses it extensively. An example is erın din laadoota, glossed by Abraham (1958) as ‘4 as-to-a-reduction off 60–10.’ Aadoota is a contraction of a longer expression meaning literally ‘10 from (20 3).’ Clearly the structure of this expression should reflect the bracketing [4[10[20 3]]]. In this structure 20 and 3 are combined by multiplication, yielding 60; after this 10 is subtracted from 60, giving 50; and finally 4 is subtracted from 50, giving 46. The last two operations performed are both subtraction. Note also that Yoruba here uses a highly unusual order for elements in a multiplicational relationship, in which the higher (base) number precedes the lower number. Almost universally in languages, the order low-before-high is preferred for numerals in a multiplicational relationship, as also for the combination numeral–noun; the combination noun-before-numeral is extremely rare.

The ancient Hawaiian system multiplied the usual bases by 4 before applying them, as shown by the numeral for 968 elua lau me eha kanahakumamawalu, literally ‘two four-hundreds and four forties and eight’ (Judd et al. 1945).

A nonstandard mathematical operation, called ‘overcounting’ is used extensively in Mayan languages and some others. An example is quoted in Hurford (1975)

Thus the numeral 41, instead of being expressed by a word meaning ‘twice twenty plus one,’ is huntuyoxkal, viz. the first (huntu) of the third score; oxkal being three times twenty, or sixty.

In a few languages, there are somewhat different numeral systems, depending on what is being counted. In Kusaiean, a Micronesian language, one system is used for counting fish and things related to fishing; another system is used for counting other things.

7. Psycholinguistic And Philosophical Aspects

There is not space here to explore some interesting psychological and philosophical questions related to number and numerals. These include: is human knowledge of number handled by domain-specific parts of the brain? Do children learn the meanings of numerals from concrete examples, such as three bricks, four teddy bears? To what extent are the universal properties of numeral systems attributable to innate dispositions in the minds of language acquirers, or are they (complementarily) conventional historic-cultural constructs? Logically, are numerals proper names or predicates? In either case, what do they denote, platonic entities or sets of collections of objects? Discussion of these issues, and more, can be found in Dehaene (1997) and Hurford (1987).

Bibliography:

1. Abraham R C 1958 Dictionary of Modern Yoruba. University of London Press, London
2. Corbett G 1978a Universals in the syntax of cardinal numerals. Lingua 46: 355–68
3. Corbett G 1978b Numerous squishes and squishy numerals in Slavonic. International Review of Slavic Linguistics 3: 43–73
4. Dehaene S 1997 The Number Sense. Oxford University Press, New York
5. Dixon R M W 1980 The Languages of Australia. Cambridge University Press, Cambridge
6. Hurford J R 1975 The Linguistic Theory of Numerals. Cambridge University Press, Cambridge, UK
7. Hurford J R 1987 Language and Number: The Emergence of a Cognitive System. Blackwell, Oxford, UK
8. Hurford J R 2001 The interaction between numerals and nouns. In: Plank F (ed.) Noun Phrase Structure in the Languages of Europe. de Gruyter, Berlin
9. Judd H P, Pukui M K, Stokes J F G 1945 Introduction to the Hawaiian Language. Tongg Publishing Company, Honolulu, HI
10. Saxe G B 1981 Bodyparts as numerals: A developmental analysis of numeration among remote Oksapmin village populations in Papua New Guinea. Child Development 52: 306–16
11. Tylor E B 1891 Primitive Culture. John Murray, London, Vol. 1