Sample The Learning Curve Research Paper. Browse other research paper examples and check the list of research paper topics for more inspiration. If you need a research paper written according to all the academic standards, you can always turn to our experienced writers for help. This is how your paper can get an A! Feel free to contact our research paper writing service for professional assistance. We offer high-quality assignments for reasonable rates.
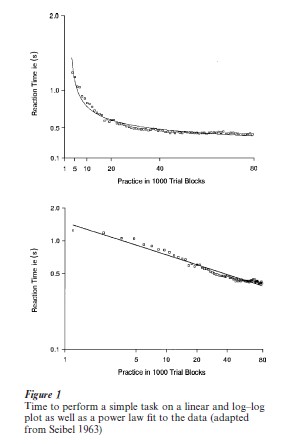
Most tasks get faster with practice. This is not surprising because we have all seen this and perhaps know it in some intuitive sense. What is surprising is that the rate and shape of improvement is fairly common across tasks. Figure 1 shows this for a simple task plotted both on linear and log–log coordinates. The pattern is a rapid improvement followed by ever lesser improvements with further practice. Such negatively accelerated learning curves are typically described well by power functions. Thus, learning is often said to follow the ‘power law of practice.’ Not shown on the graph, but occurring concurrently, is a decrease in variance in performance as the behavior reaches an apparent plateau on a linear plot. This plateau masks continuous small improvements with extensive practice that may only be visible on a log–log plot where months or years of practice can be seen. The longest measurements suggest that for some tasks improvement continues for over 100,000 trials.
Academic Writing, Editing, Proofreading, And Problem Solving Services
Get 10% OFF with 24START discount code
There are some related regularities. There is evidence to suggest that standard deviation and skew in performance time also decrease according to a power law, but with worse correlations. Indeed, in some cases the decrease in standard deviations appears to cause the improvement, because the minimum time to perform a task does not change (Rabbitt and Banerji 1989).
The power law of practice is ubiquitous. From short perceptual tasks to team-based longer term tasks of building ships, the breadth and length of human behavior, the rate that people improve with practice appears to follow a similar pattern. It has been seen in pressing buttons, reading inverted text, rolling cigars, generating geometry proofs, and manufacturing machine tools (cited in Newell and Rosenbloom 1981), performing mental arithmetic on both large and small tasks (Delaney et al. 1998), performing a scheduling task (Nerb et al. 1999), and writing books (Ohlsson 1992). Further examples are noted in reviews (e.g., Heathcote et al. 2000). In manufacturing this curve is called a progress function. It can be demonstrated by taking a task—nearly any task—and timing how long it takes to complete over 10 trials, or better over a hundred trials. An example might be to try reading this research paper upside down. The time per paragraph will generally decrease, but with some differences caused by the different words and paragraph lengths.
In general, the more averaging, the smoother the curve. The learning curve appears smoother when the data is averaged across subjects, across tasks, or both. When the tasks are known to vary in difficulty, such as different complex mental arithmetic problems (e.g., 27×5 and 23×28), the learning curve only appears when averaging is performed because the different problems naturally take different times. Even when problems are of comparable difficulty, subjects may use different strategies. For example, arithmetic problems can be solved by two at least strategies, retrieval and calculation. The power law applies across strategies, but the fit is better to each strategy (Delaney et al. 1998), or even an individual’s strategies (Heathcote et al. 2000).
Averaging can mask important aspects of learning. If the tasks vary in difficulty, the resulting line will not appear as a smooth curve, but will bounce around. Careful analysis can show that different amounts of transfer and learning are occurring on each task. For example, solving the problem 22×43 will be helped more by previously solving 22×44 than by solving 17×38 because there are more multiplications shared between them. Where subtasks are related but different, such as sending and receiving Morse code, the curves can be related but visibly different (Bryan and Harter 1897).
The learning curve has implications for learning in education and everyday life. It suggests that practice always helps improve performance, but that the most dramatic improvements happen first. Another implication is that with sufficient practice people can achieve comparable levels of performance. For example, extensive practice on mental arithmetic (Staszewski reported in Delaney et al. 1998) and on digit memorization have turned average individuals into world class performers.
To sum up, the learning curve is visible with enough aggregation of dissimilar tasks or across similar tasks down to the level of individual subject’s strategies.
1. Mathematical Definitions
The shape of the curve is negatively accelerated— further practice improves performance, but with diminishing returns. Power laws and exponentials are both functions that provide this shape. Mathematical definitions are given in Table 1. The exact quality of the fit depends on innumerable details of averaging, the precise function used, and the scale. For example, the full power law formula is the most precise, but it has additional terms that are difficult to compute, and the asymptote is usually only visible when there are over 1,000 practice trials (Newell and Rosenbloom 1981). The typical power law formula is simpler, but leaves out previous practice. When using this formula, the coefficients of the power law for a set of data can be easily computed by taking the log of the trial number and log of task time and computing a linear regression. That is, fitting a regression in log–log space.

In general, the power function fit appears to be robust, regardless of the methods used (Newell and Rosenbloom 1981). However, recent work (Heathcote et al. 2000) suggests that the power law might be an artifact arising from averaging (Anderson and Tweney 1997), and that the exponential function may be the best fit when individual subjects employing a single strategy are considered. Distinguishing between the power and exponential functions is not just an esoteric exercise in equation fitting. If learning follows an exponential, then learning is based on a fixed percentage of what remains to be learnt. If learning follows a power law, then learning slows down in that it is based on an ever decreasing percentage of what remains to be learnt.
Regardless of the functional form of the practice curve, there remain some systematic deviations that cause problems, at the beginning and end of long series. The beginning deviations may represent an encoding process. For example, it may be necessary to transform a declarative description of a task into procedures before actual practice at the task can begin (Anderson and Lebiere 1998); the residuals at the end may represent approaching the minimum time for a given task as defined by an external apparatus. These effects appear in Fig. 1 as well.
2. Process-based Explanations of the Learning Curve
The power law of learning is an important regularity of human behavior that all theories of learning must address. For example, Logan (1988) suggests that the retrieval of memory traces guides responding in speeded tasks. Response times represent the fastest retrieval time among the memory traces racing to guide the response. The power law falls out of this analysis, because with practice the number of redundant memory traces increases, which, in turn, increases the chances of observing fast retrieval times. Olhsson’s (1996) theory notes how the learning curve could arise out of error correction. Different assumptions (e.g., how fast errors are caught) give rise to different curves including the exponential and power law. The learning curve has also been demonstrated for connectionist models as well.
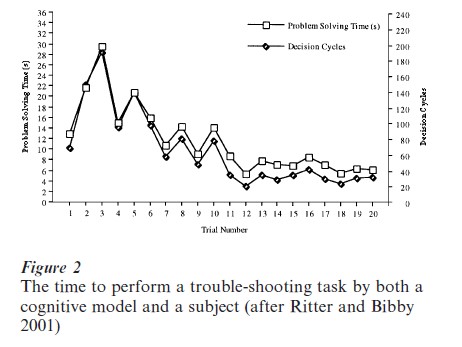
ACT-R (Anderson and Lebiere 1998) and SOAR (Newell 1990), two cognitive architectures, generally predict a power law speedup, but for different reasons. ACT-R does this because rules and memory traces are strengthened according to a power law based on the assumption that the cognitive system is adapted to the statistical structure of the environment (Anderson and Schooler 1991). Several models in SOAR have been created that model the power law (e.g., Nerb et al. 1999, Newell 1990). These models explain the power law as arising out of mechanisms such as hierarchical learning (i.e., learning parts of the environment or internal goal structure) that initially learns low-level actions that are very common and thus useful, and with further practice more useful larger patterns that occur infrequently are learned. The SOAR models typically vary from human learning in that they learn faster than humans, and they do not learn for as long a period. SOAR and ACT-R also predict variance in the improvement on all tasks due to different amounts of transfer across problems and learning episodes. Figure 2 shows how such a model can predict differential transfer as well as continuous learning as it appears in human data.
3. Summary
The learning curve is a success story for cognitive psychology, which has shown that learning is ubiquitous and has provided mathematical accounts of the rate. The learning curve is also a success story for cognitive modeling, which has explained many aspects of the curve and the noise inherent in it partly as differences in transfer of knowledge between tasks and how the curve arises out of mechanisms necessary for processing. The multiple explanations also suggest that there may be multiple ways that the curve can arise.
Bibliography:
- Anderson J R, Lebiere C 1998 The Atomic Components of Thought. Erlbaum, Mahwah, NJ
- Anderson J R, Schooler L J 1991 Reflections of the environment in memory. Psychological Science 2: 396–408
- Anderson R B, Tweney R D 1997 Artifactual power curves in forgetting. Memory and Cognition 25: 724–30
- Bryan W L, Harter N 1897 Studies in the physiology and psychology of the telegraphic language. Psychological Review 4: 27–53
- Delaney P F, Reder L M, Staszewski J J, Ritter F E 1998 The strategy specific nature of improvement: The power law applies by strategy within task. Psychological Science 9(1): 1–7
- Heathcote A, Brown S, Mewhort D J K 2000 The power law repealed: The case for an exponential law of practice. Psychonomic Bulletin and Review 7: 185–207
- Jones G, Ritter F E, Wood D J 2000 Using a cognitive architecture to examine what develops. Psychological Science 11(2): 1–8
- Logan G D 1988 Toward an instance theory of automatization. Psychological Review 95: 492–527
- Nerb J, Ritter F E, Krems J 1999 Knowledge level learning and the power law: A Soar model of skill acquisition in scheduling. In: Wallach D, Simon H A (eds.) Kognitionswissenschaft [Journal of the German Cognitive Science Society] Special issue on cognitive modeling and cognitive architectures, pp. 20–9
- Newell A 1990 Unified Theories of Cognition. Harvard University Press, Cambridge, MA
- Newell A, Rosenbloom P S 1981 Mechanisms of skill acquisition and the law of practice. In: Anderson J R (ed.) Cognitive Skills and their Acquisition. Erlbaum, Hillsdale, NJ, pp. 1–51
- Ohlsson S 1992 The learning curve for writing books: Evidence from Asimov. Psychological Science 3(6): 380–2
- Ohlsson S 1996 Learning from performance errors. Psycho- logical Review 103(2): 241–62
- Rabbitt P, Banerji N 1989 How does very prolonged practice improve decision speed? Journal of Experimental Psychology: General 118: 338–45
- Ritter F E, Bibby P A 2001 Modeling how and when learning happens in a simple fault-finding task. Proceedings of the 4th International Conference on Cognitive Modeling. Erlbaum, Mahwah, NJ
- Rosenbloom P S, Newell A 1987 Learning by chunking, a production system model of practice. In: Klahr D, Langley P, Neches R (eds.) Production System Models of Learning and Development. MIT Press, Cambridge, MA, pp. 221–86
- Seibel R 1963 Discrimination reaction time for a 1,023-alternative task. Journal of Experimental Psychology 66(3): 215–26




