Visual Perception of Objects Research Paper

This research paper describes perceptual organization and object identification in the visual modality only. This is not because either organization or identification is absent in other sensory modes—quite the contrary. But the specific stimulus information and processing mechanisms are different enough across modalities that it makes more sense to discuss them separately. The present research paper concentrates mainly on organization and identification in static scenes.

Perceptual Organization

The term perceptual organization refers somewhat ambiguously both to the structure of experiences based on sensory activity and to the underlying processes that produce that perceived structure. The importance and difficulty of achieving useful organization in the visual modality can perhaps be most easily appreciated by considering the output of the retinal mosaic simply as a numerical array, in which each number represents the neural response of a single receptor. The main organizational problem faced by the visual nervous system is to determine object structure: what parts of this array go together, so to speak, in the sense of corresponding to the same objects, parts, or groups of objects in the environment. This way of stating the problem implies that much of perceptual organization can be understood as the process by which a part-whole hierarchy is constructed for an image (Palmer, in press-b). There is more to perceptual organization than just part-whole structure, but it seems to be the single most central issue.

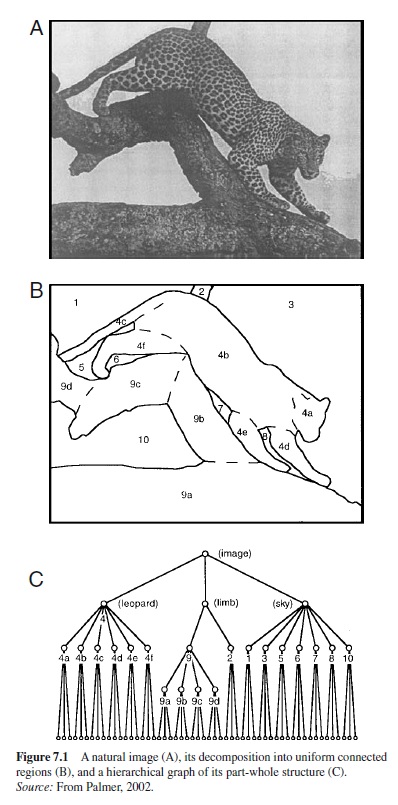
The first problem, therefore, is to understand what partwhole structure people perceive in a given scene and how it might be characterized. Logically, there are limitless possible organizations for any particular image, only one (or a few) of which people actually perceive. A possible part-whole structure for the leopard image in Figure 7.1 (A) is given in Figure 7.1 (C). It is represented as a hierarchical graph in which each node stands for a perceptual unit or element, and the various labels refer to the image regions distinguished in Figure 7.1 (B). The top (or root) node represents the entire image. The scene is then divided into the leopard, the branch, and the background sky. The leopard is itself a complex perceptual object consisting of its own hierarchy of parts: head, body, tail, legs, and so forth. The branch also has parts consisting of its various segments. The sky is articulated into different regions in the image, but it is perceptually uniform because it is completed behind the leopard and branches. The bottom (or terminal) nodes of the graph represent the millions of individual receptors whose outputs define this particular optical image.

The second problem is how such a part-whole hierarchy might be determined by the visual system. This problem, in turn, has at least three conceptual parts. One is to understand the nature of the stimulus information that the visual system uses to organize images. This includes not only specifying the crucial stimulus variables, but also determining their ecological significance: why they are relevant to perceiving partwhole structure. It corresponds to what Marr (1982) called a “computational” analysis. The second problem is to specify the processing operations involved in extracting this information: how a particular organization is computed from an image via representations and processes. It corresponds to what Marr called an “algorithmic” analysis. The third is to determine what physiological mechanisms perform these operations in the visual nervous system. It corresponds to what Marr called an “implementational” analysis. As we shall see, we currently know more about the computational level of perceptual organization than about the algorithmic level, and almost nothing yet about the neural implementation.

Perceptual Grouping

The visual phenomenon most closely associated historically with the concept of perceptual organization is grouping: the fact that observers perceive some elements of the visual field as “going together” more strongly than others. Indeed, perceptual grouping and perceptual organization are sometimes presented as though they were synonymous. They are not. Grouping is one particular kind of organizational phenomenon, albeit a very important one.

Principles of Grouping

The Gestalt psychologist Max Wertheimer first posed the problem of perceptual organization in his groundbreaking 1923 paper. He then attempted a solution at what would now be called the computational level by asking what stimulus factors influence perceived grouping of discrete elements. He first demonstrated that equally spaced dots do not group together into larger perceptual units, except the entire line (Figure 7.2; A). He then noted that when he altered the spacing between adjacent dots so that some dots were closer than others, the closer ones grouped together strongly into pairs (Figure 7.2; B). This factor of relative distance, which Wertheimer called proximity, was the first of his famous laws or (more accurately) principles of grouping.

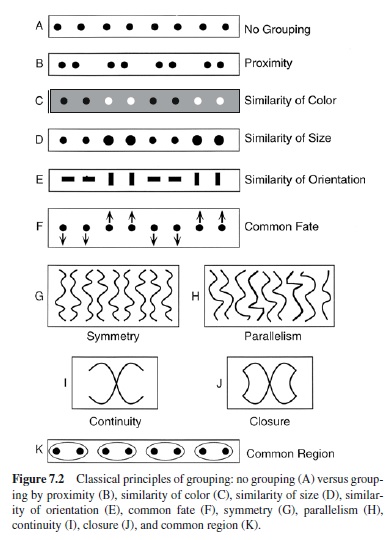
Wertheimer went on to illustrate other grouping principles, several of which are portrayed in Figure 7.2. Parts C, D, and E demonstrate different versions of the general principle of similarity: All else being equal, the most similar elements (in color, size, and orientation for these examples) tend to be grouped together. Another powerful grouping factor is common fate: All else being equal, elements that move in the same way tend to be grouped together. Notice that both common fate and proximity can actually be considered special cases of similarity grouping in which the relevant properties are similarity of velocity and position, respectively. Further factors that influence perceptual grouping of more complex elements, such as lines and curves, include symmetry (Figure 7.2; G), parallelism (Figure 7.2; H), and continuity or good continuation (Figure 7.2; I). Continuity is important in Figure 7.2 (I) because observers usually perceive it as containing two continuous intersecting lines rather than as two angles whose vertices meet at a point. Figure 7.2 (J) illustrates the further factor of closure: All else being equal, elements that form a closed figure tend to be grouped together. Note that this display shows that closure can overcome continuity because the very same elements that were organized as two intersecting lines in part I are organized as two angles meeting at a point in part J.

Recently, two new grouping factors have been suggested: common region (Palmer, 1992) and synchrony (Palmer & Levitin, 2002). Common region refers to the fact that, all else being equal, elements that are located within the same closed region of space tend to be grouped together. Figure 7.2 (K) shows an example analogous to Wertheimer’s classic demonstrations (Figures 7.2; B–F): Otherwise equivalent, equallyspaceddotsarestronglyorganizedintopairswhentwo adjacent elements are enclosed within the same surrounding contour.

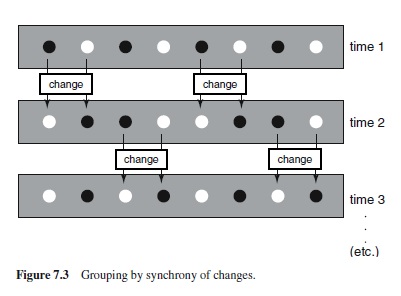
The principle of synchrony states that, all else being equal, visual events that occur at the same time tend to be perceived as grouped (Palmer & Levitin, 2002). Figure 7.3 depicts an example similar to those in Figure 7.2 (B–F). Each element in an equally spaced row of dots flickers alternately between dark and light. The arrows indicate that half the circles change color at one time and the other half at a different time. When the alternation rate is about 5–25 changes per second or fewer, observers see the dots as strongly grouped into pairs based on the synchrony of these changes. At much faster rates, there is no grouping among what appear to be chaotically flickering dots. At much slower rates, there is momentary grouping into pairs when the changes occur, but the grouping dissipates during the unchanging interval between them. Synchrony is related to the classical principle of common fate in the sense that it is a dynamic factor, but, as this example shows, the “fate” of the elements does not have to be common: Some dots get brighter and others get dimmer. Synchrony grouping can even occur when the elements change along different dimensions, some changing brightness, others changing size, and still others changing orientation.

One might think that grouping principles are mere textbook curiosities only distantly related to anything that occurs in normal perception. On the contrary, they pervade virtually all perceptual experiences because they determine the objects and parts we perceive in the environment. Dramatic examples of perceptual organization going wrong can be observed in natural camouflage. The leopard in Figure 7.1 (A) is not camouflaged against the uniform sky, but if it were seen against a mottled, leafy backdrop, it would be very difficult to see—until it moved. Even perfect static camouflage is undone by the principle of common fate. The common motion of its markings and contours against the stationary background causes them to be strongly grouped together, providing an observer with enough information to perceive it as a distinct object against its unmoving background.

Successful camouflage also reveals the ecological rationale for the principles of grouping: finding objects. Camouflage results when the same grouping processes that would normally make an organism stand out from its environment as a separate object cause it to be grouped with its surroundings instead. This results primarily from similarity grouping of various forms, when the color, texture, size, and shape of the organism are similar enough to those of the objects in its environment to be misgrouped.

Integrating Multiple Principles of Grouping

The demonstrations of continuity and closure in Figure 7.2 (I and J) illustrate that grouping principles, as formulated by Wertheimer (1923/1950), are ceteris paribus rules: Theypredicttheoutcomeofgroupingwithcertaintyonlywhen everything else is equal—that is, when no other grouping factor opposes its influence.We saw, for example, that continuity governs grouping when the elements do not form a closed figure, but continuity can be overcome by closure when they do (Figure 7.2; I vs. J). The difficulty with ceteris paribus rules is that they provide no scheme for integrating multiple factors into an overall outcome—that is, for predicting the strength of their combined effects. The same problem arises for all of the previously mentioned principles of grouping as well. If proximityinfluencesgroupingtowardoneoutcomeandcolorsimilarity toward another, which grouping will be perceived depends heavily on the particular degrees of proximity and color similarity (e.g., Hochberg & Silverstein, 1956).

Recent work by Kubovy and his colleagues has begun to address this problem. Kubovy and Wagemans (1995) measured the relative strength of different groupings in dot lattices (Figure 7.4; A) by determining the probability with which subjects reported seeing them organized into lines in each of the four orientations indicated in Figure 7.4 (B). After seeing a given lattice for 300 ms, subjects indicated which of the four organizations they perceived so that, over many trials, the probability of perceiving each grouping could be estimated. Consistent with the Gestalt principle of proximity, their results showed that the most likely organization is the one in which the dots are closest together, with other organizations being less likely as the spacing between the dots increased.

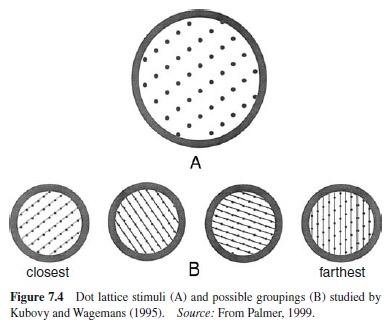
More precisely, Kubovy and Wagemans (1995) found that their data were well fit by a mathematical model in which the attraction between dots decreases exponentially as a function of distance:

where f(v) is the attraction between two elements in the lattice as a function of the distance, v, between them, α is a scaling constant, and a is shortest distance between any pair of elements. Further experiments using lattices in which the dots differed in color similarity as well as proximity showed that the rule by which multiple grouping factors combine is multiplicative (see Kubovy & Gepstein, 2000). This finding begins to specify general laws by which multiple factors can be integrated into a combined result.

Is Grouping an Early or Late Process?

If perceptual organization is to be understood as the result of computations, the question of where grouping occurs in the stream of visual processing is important. Is it an early process that works at the level of two-dimensional image structure or does it work later, after depth information has been extracted and perceptual constancy has been achieved? (Perceptual constancy refers to the ability to perceive the unchanging properties of distal environmental objects despite variation in the proximal retinal images caused by differences in viewing conditions) Wertheimer (1923) discussed grouping as though it occurred at a low level, presumably corresponding to what is now called image-based processing (see Palmer, 1999). The view generally held since Wertheimer’s seminal paper has been that organization must occur early to provide virtually all higher level perceptual processes with discrete units as input (e.g., Marr, 1982; Neisser, 1967).

Rock and Brosgole (1964) reported evidence against the early-only view of grouping, however. They examined whether the relevant distances for grouping by proximity are defined in the two-dimensional image plane or in perceived three-dimensional space. They showed observers a twodimensional rectangular array of luminous beads in a dark room either in the frontal plane (perpendicular to the line of sight) or slanted in depth, so that the horizontal dimension was foreshortened to a degree that depended on the angle of slant. The beads were actually closer together vertically,sothatwhen they were viewed in the frontal plane, observers saw them grouped into vertical columns rather than horizontal rows.

The crucial question was what would happen when the same lattice of beads was presented to the observer slanted in depth so that the beads were closer together horizontally when measured in the retinal image, even though they are still closer together vertically when measured in the threedimensional environment. When observers viewed this slanted display with just one eye, so that binocular depth information was not available, they reported that the beads were organized into rows. But when they perceived the slant of the lattice in depth by viewing the same display binocularly, their reports reversed: They now reported seeing the slanted array of beads organized into vertical columns. This finding thus supports the hypothesis that final grouping occurs after stereoscopic depth perception.

Rock, Nijhawan, Palmer, and Tudor (1992) addressed a similar issue in lightness perception.Their results showed that grouping followed the predictions of a late (postconstancy) grouping hypothesis: Similarity grouping in the presence of shadows and translucent overlays was governed by the perceived lightnesses of the elements rather than by their retinal luminances. Further findings using analogous methods have shown that perceptual grouping is also strongly affected by amodal completion (Palmer, Neff, & Beck, 1996) and by illusory contours (Palmer & Nelson, 2000), both of which are believed to depend on depth perception in situations of occlusion (see Rock, 1983). (Amodal completion is the process by which partly occluded surfaces of objects are perceived as continuing behind the occluding object, as illustrated in Figure 7.10, and illusory contours are edges that are perceived wherethereisnophysicalluminancegradientpresentbecause the occluding surface is the same color as the occluded surface, as illustrated in Figure 7.13. See section entitled “Visual Interpretation” for further information.) Such results show that grouping cannot be attributed entirely to early, preconstancy visual processing, but they are also compatible with the possibility that grouping is a temporally extended process that includes components at both early and later levels of processing (Palmer, in press-a). A provisional grouping might be determined at a nearly, preconstancy stage of image processing, but might be overridden if later, object-based information (from depth, lighting conditions, occlusion, etc.) required it.

Before leaving the topic of early versus late grouping, it is worth noting that Wertheimer (1923) discussed a further factor in perceptual grouping that is seldom mentioned: past experience. The idea is that elements that have been previously grouped in certain ways will tend to be seen as grouped in the same way when they are seen again. According to modern visual theory, such effects would also support the hypothesis that grouping effects can occur relatively late in perception, because they would have to happen after contact has been made between the information in the stimulus display and representations in memory.

Figure 7.5 provides a particularly strong demonstration of the effects of prior experience. People who have never seen this image before usually perceive it as a seemingly random array of meaningless black blobs on a white background. After they have discerned the Dalmatian with its head down, sniffing along a street, however, the picture becomes dramatically reorganized, with certain of the blobs going together because they are part of the dog and others going together because they are part of the street or the tree. The interesting fact relevant to past experience is that after you have seen the Dalmatian in this picture, you will see it that way for the rest of your life! Past experience can thus have a dramatic effect on grouping and organization, especially if the organization of the image is highly ambiguous.

Region Segmentation

There is an important logical gap in the story of perceptual organization that we have told thus far. No explanation has been given of how the to-be-grouped “elements” (e.g., the dots and lines in Figure 7.2) arise in the first place. Wertheimer (1923/1950) appears simply to have assumed the existence of such elements, but notice that they are not directly given by the stimulus array. Rather, their formation requires an explanation, including an analysis of the factors that govern their existence as perceptual elements and how such elements might be computed from an optical array of luminance values. This initial organizational operation is often called region segmentation: the process of partitioning an image into an exhaustive set of mutually exclusive twodimensional areas.

Uniform Connectedness

Palmer and Rock (1994a, 1994b) suggested that region segmentation is determined by an organizational principle that they called uniform connectedness. They proposed that the first step in constructing the part-whole hierarchy for an image is to partition the image into a set of uniformly connected (UC) regions, much like a stained glass window. A region is uniformly connected if it constitutes a single, connected subset of the image that is either uniform or slowly varying in its visual properties, such as color, texture, motion, and binocular disparity. Figure 7.1 (B) shows a plausible set of UC regions for the leopard image, bounded by the solid contours and labelled as regions 1 through 10.

Uniform connectedness is an important principle of perceptual organization because of its informational value in designating connected objects or object parts in the environment. As a general rule, if an area of the retinal image constitutes a UC region, it almost certainly comes from the light reflected from a single, connected, environmental object or part. This is not true for successful camouflage, of course, but such situations are comparatively rare. Uniform connectedness is therefore an excellent heuristic for finding image regions that correspond to parts of connected objects in the environment.

Figure 7.6 (B) shows how an image of a penguin (Figure 7.6; A) has been divided into a possible set of UC regions by a global, explicitly region-based procedure devised by Malik and his colleagues (Leung & Malik, 1998; Shi & Malik, 1997). Their “normalized cuts” algorithm is a graph theoretic procedure that works by finding the binary partition of a given region—initially, the whole image—into two sets of pixels that maximizes a particular measure of pairwise pixel similarity within the same subregion, normalized relative to the total pairwise pixel similarity within the entire region. Similarity of pixel pairs is defined in their algorithm by the weighted integration of a number of Gestalt-like grouping factors, such as proximity, color similarity, texture similarity, and motion similarity. They also include a grouping factor based on evidence for the presence of a local edge between the given pair of pixels, which reduces the likelihood that they are part of the same subregion. When this normalized cuts algorithm is applied repeatedly to a given image, dividing and subdividing it into smaller and smaller regions, perceptually plausible partitions emerge rapidly (Figure 7.6; B). Notice that Malik’s region-based approach produces closed regions by definition.

Another possible approach to region segmentation is to begin by detecting luminance edges. Whenever such edges form a closed contour, they define two regions: the fully bounded interior and the partly bounded exterior. An image can therefore be segmented into a set of connected regions by using an edge-detection algorithm to locate closed contours. This idea forms a theoretical bridge between the well-known physiological and computational work on edge detection (e.g., Canny, 1986; Hubel & Wiesel, 1962; Marr & Hildreth, 1980) and work on perceptual organization, suggesting that edge detection may be viewed as the first step in region segmentation. An important problem with this approach is that most edge-detection algorithms produce few closed contours, thus requiring further processing to link them into closed contours. The difficulty is illustrated in Figure 7.6 (C) for the output of Canny’s (1986) well known edge-detection algorithm.

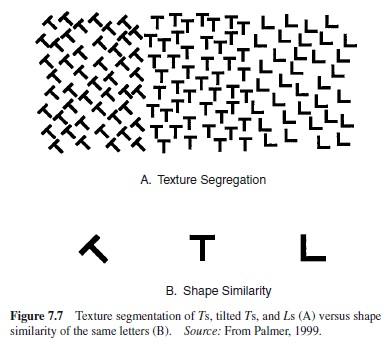
Texture Segmentation

A special case of region segmentation that has received considerable attention is texture segmentation (e.g., Beck, 1966, 1972, 1982; Julesz, 1981). In Figure 7.1(A), for example, the leopard is not very different in overall luminance from the branch, but the two can easily be distinguished visually by their different textures.

The factors that govern region segmentation by texture elements are not necessarily the same as those that determine explicit judgments of shape similarity, even for the very same texture elements when they are perceived as individual figures. For instance, the dominant texture segmentation evident in Figure 7.7 (A)—that is to say, that separating the upright Ts and Ls from the tilted Ts—is the opposite of simple shape similarity judgments (Figure 7.7; B) in which a single upright T was judged more similar to a tilted T than it was to an upright L (Beck, 1966). From the results of many such experiments, texture segmentation is believed to result from detecting differences in feature density (i.e., the number of features per unit of area) for certain simple attributes, such as line orientation, overall brightness, color, size, and movement (Beck, 1972). Julesz (1981) later proposed a similar theory in which textures were segregated by detecting changes in the density of certain simple, local textural features that he called textons (Julesz, 1981), which included elongated blobs defined by their color, length, width, orientation, binocular disparity, and flicker rate, plus line terminators and line crossings or intersections.

Julesz also claimed that normal, effortless texture segmentation based on differences in texton densities was a preattentive process: one that occurs automatically and in parallel over the whole visual field prior to the operation of focussed attention. He further suggested that there were detectors early in the visual system that are sensitive to textons such that texture segmentation takes place through the differential activation of the texton detectors. Julesz’s textons are similar to the critical features ascribed to simple cells in cortical area V1 (Hubel & Wiesel, 1962), and to some of the primitive elements in Marr’s primal sketch (Marr, 1982; Marr & Nishihara, 1978). Computational theories have since been proposed that perform texture segmentation by detecting textural edges from the outputs of quasi-neural elements whose receptive fields are like those found in simple cells of area V1 of the visual cortex (e.g., Malik & Perona, 1990).

Figure-Ground Organization

If the goal of perceptual organization is to construct a scenebased hierarchy consisting of parts, objects, and groups, region segmentation can be no more than a very early step, because uniform connected regions in images seldom correspond directly to the projection of whole environmental objects. As is evident from Figures 7.1 (A, B, and C), some UC regions need to be grouped into higher-level units (e.g., the various patches of sky) and others need to be parsed into lower-level units (e.g., the various parts of the leopard) to construct a useful part-whole hierarchy. But before any final grouping and parsing can occur, boundaries must be assigned to regions.

Boundary Assignment

For every bounding contour in a segmented image there is a region on both sides. Because most visible surfaces are opaque, the region on one side usually corresponds to a closer, occluding surface, and the region on the other side to a farther, occluded surface that extends behind the closer one. Boundary assignment is the process of determining to which region the contour belongs, so to speak, thus determining the shape of the closer surface, but not that of the farther surface.

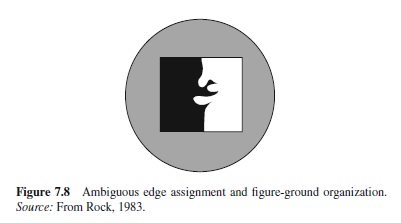
To demonstrate the profound difference that alternative boundary assignments can make, consider Figure 7.8. Region segmentation processes will partition the square into two UC regions, one white and the other black. But to which side does the central boundary belong? If you perceive the edge as belonging to the white region, you will see a white object with rounded fingers protruding in front of a black background. If you perceive the edge as belonging to the black region, you will see a black object with pointed claws in front of a white background. This particular display is highly ambiguous, so that sometimes you see the white fingers and other times the black claws. (It is also possible to see a mosaic organization in which the boundary belongs to both sides at once, as in the case of jigsaw puzzle pieces that fit snugly together to form a single contour. This interpretation is infrequent, probably because it does not arise very often in normal situations, except when two adjacent, parallel contours are clearly visible.) This boundary-assignment aspect of perceptual organization is known in the classical perception literature as figure-ground organization (Rubin, 1921). The “thing-like” region is referred to as the figure and the “background-like” region as the ground.

Principles of Figure-Ground Organization

Figure 7.8 is highly ambiguous in its figure-ground organization because it is about equally easy to see the back and white regions as figure, but this is not always, or even usually, the case. The visual system has distinct pBibliography: for perceiving certain kinds of regions as figural, and these are usually sufficient to determine figure-ground organization. Studies have determined that the following factors are relevant, all of which bias the region toward being seen as figural: surroundedness, smaller size, horizontal-vertical orientation, lower region (Vecera,Vogel, & Woodman, in press), higher contrast, greater symmetry, greater convexity (Kanisza & Gerbino, 1976), parallel contours, meaningfulness (Peterson & Gibson, 1991), and voluntary attention (Driver & Baylis, 1996). Analogous to the Gestalt principles of perceptual grouping, these principles of figure-ground organization are ceteris paribus rules—, rules in which a given factor has the stated effect, if all other factors are equal (i.e., eliminated or otherwise neutralized). As such, they have the same weaknesses as the principles of grouping, including the inability to predict the outcome when several conflicting factors are at work in the same display.

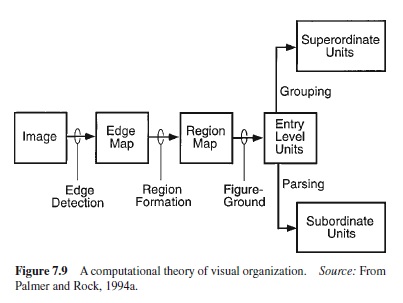
In terms of information processing structure, Palmer and Rock (1994a, 1994b) proposed a process model of perceptual organization in which figure-ground organization occupies a middle position, occurring after region segmentation, but before grouping and parsing (see Figure 7.9). They argued that figure-ground processing logically must occur after region-segmentation processing because segmented regions are required as input by any algorithm that discriminates figure from ground. The reason is that most of the principles of figure-ground organization—for example, surroundedness, size, symmetry, and convexity—are properties that are only defined for two-dimensional regions, and thus require twodimensional regions as input. More speculatively, Palmer and Rock (1994a, 1994b) also claimed that figure-ground organization must logically precede grouping and parsing. The reason is that the latter processes, which apparently depend on certain shape-based properties of the regions in question— for example, concavity-convexity, similarity of orientation, shape, size, and motion—require prior boundary assignment. Grouping and parsing thus depend on shape properties that are logically well-defined for regions only after boundaries have been assigned, either to one side or perhaps initially to both sides (Peterson & Gibson, 1991).

Parsing

Another important process involved in the organization of perception is parsing or part segmentation: dividing a single element into two or more parts. This is essentially the opposite of grouping. Parsing is important because it determines what subregions of a perceptual unit are perceived as belonging together most coherently. To illustrate, consider the leopard in Figure 7.1 (A). Region segmentation might well define it as a single region based on its textural similarity (region 4), and this conforms to our experience of it as a single object. But we also experience it as being composed of several clear and obvious parts: the head, body, tail, and three visible legs, as indicated by the dashed lines in Figure 7.1 (B). The large, lower portion of the tree limb (region 9) is similarly a single UC region, but it too can be perceived as divided (although perhaps less strongly) into the different sections indicated by dotted lines in Figure 7.1 (B).

Palmer and Rock (1994a) argued that parsing must logically follow region segmentation because parsing presupposes the existence of a unitary region to be divided. Since they proposed that region segmentation is the first step in the process that forms such region-based elements, they naturally argued that parsing must come after it. There is no logical constraint, however, on the order in which parsing and grouping must occur relative to each other. They could very well happen simultaneously. This is why the flowchart of Palmer and Rock’s theory (Figure 7.9) shows both grouping and parsing taking place at the same time after regions have been defined. According to their analysis, parsing should also occur after figure-ground organization. The reason is that parsing, like grouping, is based on properties (such as concavity-convexity) that are properly attributed to regions only after some boundary assignment has been made. There is no point in parsing a background region at concavities along its border if that border does not define the shape of the corresponding environmental object, but only the shape of a neighboring object that partly occludes it.

There are at least two quite different ways to go about dividing an object into parts: boundary rules and shape primitives. The boundary rule approach is to define a set of general conditions that specify where the boundaries lie between parts. The best known theory of this type was developed by Hoffman and Richards (1984). Their key observation was that the two-dimensional silhouettes of multipart objects can usually be divided at deep concavities: places where the contour of an object’s outer border is maximally curved inward (concave) toward the interior of the region. Formally, these points are local negative minima of curvature.

An alternative to parsing by boundary rules is the shape primitive approach. It is based on a set of atomic, indivisible shapes that constitute a complete listing of the most basic parts. More complex objects are then analyzed as configurations of these primitive parts. This process can be thought of as analogous to dividing cursively written words into parts by knowing the cursive alphabet and finding the primitive component letters. Such a scheme for parsing works well if there is a relatively small set of primitive components, as there is in the case of cursive writing. It is far from obvious, however, what the two-dimensional shape primitives might be in the caseofparsingtwo-dimensionalprojectionsofnaturalscenes.

If the shape primitive approach is going to work, it is natural that the shape primitives appropriate for parsing the projected images of three-dimensional objects should be the projections of three-dimensional volumetric shape primitives. Such an analysis has been given in Binford’s (1971) proposal that complex three-dimensional shapes can be analyzed into configurations of generalized cylinders: appropriately sized and shaped volumes that are generalized from standard cylinders in the sense that they have extra parameters that enable them to describe many more shapes. The extra parameters include ones that specify the shape of the base (rather than always being circular), the curvature of the axis (rather than always being straight), and so forth (see also Biederman, 1987; Marr, 1982). The important point for present purposes is that if one has a set of shape primitives and some way of detecting them in two-dimensional images, complex three-dimensional objects can be appropriately segmented into primitive parts. Provided that the primitives are sufficiently general, part segmentation will be possible, even for novel objects.

Visual Interpolation

With the four basic organizational processes discussed thus far—region segmentation, figure-ground organization, grouping, and parsing—it is possible to see how a rudimentary part-whole hierarchy might be constructed by some appropriate sequence of operations. One of the main further problems that the visual system must solve is how to perceive partly occluded objects as such. In Figure 7.1 (A), for example, the part of the branch above the leopard is perceived as the extension of the branch below it. This is more than simple grouping of the two corresponding image regions because the observer completes the branch in the sense of perceiving that it continues behind the leopard. The various patches of sky between and around the leopard and branches must likewise be perceived as parts of the uninterrupted sky behind them. The crucial ecological fact is that most environmental surfaces are opaque and therefore hide farther surfaces from view. What is needed to cope with the incomplete, piecewise, and changeable montage of visible surfaces that stimulate the retina is some way to infer the nature of hidden parts from visible ones.

The visual system has evolved mechanisms to do this, which will be referred to collectively as processes of visual interpolation (Kellman & Shipley, 1991). They have limitations, primarily because all they can do is make a best guess about something that can be only partly seen. Completely occluded objects are seldom interpolated, even if they are present, because there is no evidence from which to do so, and even partly visible objects are sometimes completed incorrectly. Nevertheless, people are remarkably adept at perceiving the nature of partly occluded objects, and this ability requires explanation.

Amodal Completion

Amodal completion is the process by which the visual system infers the nature of hidden parts of partly occluded surfaces and objects from their visible projections. It is called amodal because there is no direct experience of the hidden part in any sensory modality; it is thus experienced amodally. A simple example is provided in Figure 7.10 (A). Observers spontaneously perceive a full circle behind a square, as indicated in Figure 7.10 (B), even though one quarter of the circle is not visible.

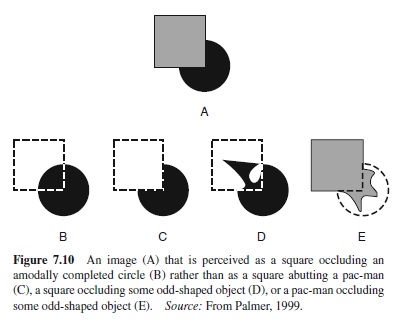
Amodal completion is logically underdetermined.The real environmental state of affairs corresponding to Figure 7.10 (A) might be a square covering a whole circle (B), a mosaic, of a square abutting a three-quarter circle (or pac-man; C), or a square in front of a circle with odd protrusions (D). It might also be a pac-man in front of a square with odd protrusions (E), or an infinite number of other possibilities. The visual system therefore appears to have strong pBibliography: about how to complete partly occluded objects, aimed at maximizing veridical perception of whole objects in the world. There are at least three general types of explanations of how this might happen.

One possibility is that the visual system completes the circle behind the square based on frequency of prior experiences. Although people have all seen three-quarter circles, most have probably seen a good many more full circles. Perhaps people complete partly occluded figures according to the most frequently encountered shape compatible with the visible stimulus information. Novel shapes can also be amodally completed (e.g., Gregory, 1972), however. This shows that familiarity cannot be the whole story, although it may be part of it.

A second possibility is that partly occluded figures are completed in the way that results in the simplest perceived figures. For example, a square occluding a complete circle in Figure 7.10 (A) is simpler than any of the alternatives in this set of completions, and the same could be true for the possible completions of novel shapes. Explaining phenomena of perceptual organization in terms of maximizing simplicity— or, equivalently, minimizing complexity—was the theoretical approach favored by Gestalt psychologists (e.g., Koffka, 1935). They called this proposal the principle of Prägnanz, which was later dubbed the minimum principle (Hochberg & McAlister, 1953): The percept will be as good or as simple, as the prevailing conditions allow.

Gestaltists were never very clear about just what constituted goodness or simplicity, but later theorists have offered explicit computational theories that are able to show that many completion phenomena can be predicted by minimizing representational complexity (e.g., Buffart & Leeuwenberg, 1981; Leeuwenberg, 1971, 1978). One problem faced by such theories is that they are only as good as the simplicity metric on which they are based. Failure to predict experimental results can thus easily be dismissed on the grounds that a better simplicity measure would bring the predictions into line with the results. This may be true, of course, but it makes a theory difficult to falsify.

A third possibility is to explain amodal completion by appealing directly to ecological evidence of occlusion. For example, when a contour of one object is occluded by that of another, they typically form an intersection known as a T-junction. The top of the T is interpreted as the closer edge whose surface occludes those surfaces adjacent to the stem of the T. The further assumptions required to account for amodal completion are that the occluded edge (and the surface attached to it) connects with another occluded edge in the scene and a set of specifications about how they are to be joined.

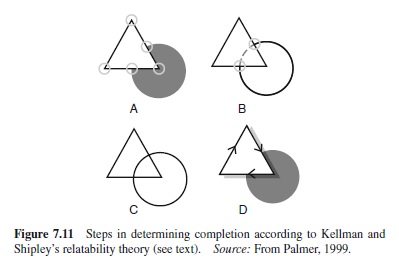
One such theory of completion is Kellman and Shipley’s (1991) relatability theory. It can be understood as a more complete and well-specified extension of the classic grouping principle of good continuation (Wertheimer, 1923/1950). The basic principles of relatability theory are illustrated in Figure 7.11. The first step is to locate all edge discontinuities, which are discontinuities in the first derivative of the mathematical function that describes the edge over space. These are circled in Figure 7.11 (A). The second is to relate pairs of edges if and only if (a) their extensions intersect at an angle of 90° or more, and (b) they can be smoothly connected to each other, as illustrated in Figure 7.11 (B). Third, a new perceptual unit is formed when amodally completed edges form an enclosed area, as shown in Figure 7.11 (C). Finally, units are assigned positions in depth based on available depth information, as depicted in Figure 7.11 (D). In completion, for example, depth information from occlusion specifies that the amodally completed edges are behind the object at whose borders they terminate. This depth assignment is indicated in Figure 7.11 (D) by arrows that point along the edge in the direction for which the nearer region is on the right.

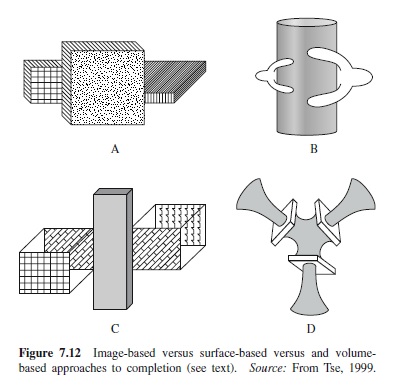
Kellman and Shipley’s (1991) relatability theory of amodal completion is couched in terms of image-based information: the existence of edge discontinuities and their twodimensional relatability in terms of good continuation. Other, more complex approaches are possible, however. One is that completion takes place within a surface-based representation by relating two-dimensional surfaces embedded in threedimensional space (Nakayama, He, & Shimojo, 1995). Another is that it occurs in an object-based representation when three-dimensional volumes are merged (Tse, 1999). Recent evidence supports the hypothesis that the final perception of amodal completion is based on merging volumes (Tse, 1999). Figure 7.12 provides evidence against both image-based and surface-based views. Part A shows an example in which the outer contours on the left and right side of the closest object line up perfectly, thus conforming to the requirements of edge relatability, yet they fail to support amodal completion. Figure 7.12(B)showstheoppositesituation,inwhichthereareno relatable contours (because they are themselves occluded), yet people readily perceive amodal completion behind the cylinder. These examples thus show that relatable contours at the level of two-dimensional images are neither necessary nor sufficient for perceiving amodal completion.

Figure 7.12 (C) shows a case in which there are relatable surfaces on the left and right sides of the occluder, and yet people perceive two distinct objects, rather than one that is completed behind it. Finally, Figure 7.12 (D) shows an example in which there are no relatable surfaces, yet amodal completion is perceived. These two example therefore show that relatable surfaces are neither necessary nor sufficient for perceiving amodal completion. Tse (1999) has argued persuasively from such examples that completion is ultimately accomplished by merging inferred three-dimensional volumes.

Illusory Contours

Another important form of visual interpolation produces a striking illusion in which contours are seen that do not actually exist in the stimulus image. This phenomenon of illusory contours (also called subjective contours) was first described almost a century ago (Schumann, 1904), but modern interest in it was sparked by the elegant demonstrations of Kanizsa (1955, 1979). One of the best known examples is the socalled Kanizsa triangle shown in Figure 7.13. The white triangle so readily perceived in this display is defined by illusory contours because the stimulus image consists solely of three pac-man–shaped figures. Most observers report seeing well-defined luminance edges where the contours of the triangle should be, with the interior region of the triangle appearing lighter than the surrounding ground. These edges and luminance differences simply are not present in the optical image.

Recent physiological research has identified cells in cortical area V2 that appear to respond to the presence of illusory contours. Cells in area V2 have receptive fields that do not initially appear much different from those in V1, but careful testing has shown that about 40% of the orientation selective cells in V2 also fire when presented with stimuli that induce illusory contours in human perception (von der Heydt, Peterhans, & Baumgartner, 1984; Peterhans & von der Heydt, 1991). Sometimes the orientational tuning functions of the cells to real and illusory contours are similar, but often they are not. Exactly how the responses of such cells might explain the known phenomena of illusory contours is not yet clear, however.

Perceived Transparency

Another phenomenon of visual interpolation is perceived transparency: the perception of objects as being viewed through a closer, translucent object that transmits some portion of the light reflected from the farther object rather than blocking it entirely. Under conditions of translucency, the light striking the retina at a given location provides information about at least two different external points along the same viewer-centered direction: one on the farther opaque surface and the other on the closer translucent surface (Figure 7.14; A).

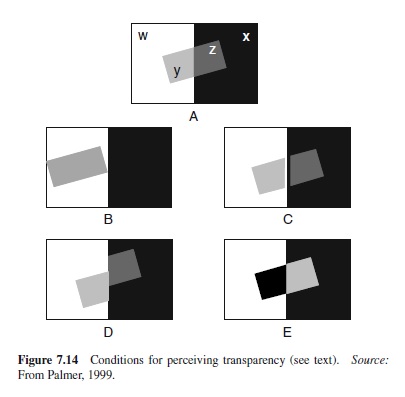
Perception of transparency depends on both spatial and color conditions. Violating the proper relations of either sort is sufficient to block it. For example, transparency will be perceived if the translucent surface is positioned so that reflectance edges on the opaque surface behind it can be seen both through the translucent surface and outside it, as illustrated in Figure 7.14 (A). When this happens, a phenomenon called color scission or color splitting occurs, and the image colors in the regions of the translucent surface are perceived as a combination of one color belonging to the background and one color belonging to the translucent surface. Color scission will not occur, however, if the translucent surface lies completely within a single reflectance region, as illustrated in Figure 7.14 (B). It can also be blocked by destroying the unity of the translucent region (Figure 7.14; C) or merely weakening it (Figure 7.14; D).

When color scission occurs, the perceived color in each region of overlap is split into a component from the transparent layer and a component from the opaque layer. For this to happen, the components due to the transparent layer must be the same. Metelli (1974), Gerbino (1994), and Anderson (1997) have precise, quantitative theories of the conditions for transparency to be perceived. Violating these constraints also blocks perceived transparency (Figure 7.14; E).

Figural Scission

Yet another example of visual interpolation isfigural scission: the division of a single homogeneous region into two overlapping figures of the same color,one in front of and occluding the other. This phenomenon, illustrated in Figure 7.15, has many interesting features. One is that there is no local sensory information that requires the single region to be split at all. The visual system constructs illusory contours where the closer figure occludes the farther one. The visual system also completes the portions of the farther figure that are occluded by the closer one. But because the stimulus conditions do not determine which figure is in front and which behind, either possibility can be perceived. Indeed, if you view such displays for awhile, the depth relations of the two parts spontaneously reverse.

Parts and Wholes

Assuming that objects are indeed perceived as structured into something like a hierarchy of objects, parts, subparts, and so on (cf. Palmer, 1977; Reed & Johnsen, 1975), a question that naturally arises is whether parts are perceived before wholes or wholes before parts. Although Gestaltists never posed the question in precisely this form, their approach to perception suggests that wholes may be processed first in some important sense. Most other approaches to perception imply the opposite: that wholes are constructed by integrating local information into increasingly larger aggregations. Even physiological evidence seems to support a local-first view. Retinal receptors respond to exceedingly tiny regions of stimulation, and as one traces the path of neural information processing, synapse by synapse, deeper into the brain, the receptive fields of visual neurons become ever larger and responsive to ever more complex stimulus configurations (e.g., Van Essen & De Yoe, 1995).

There are problems in accepting this line of argument as settling anything about perceptual experience, however. First, the order in which processing is initiated may not be nearly as relevant for perceptual experience as the order in which it is completed. Although it is clear that neural processing is initiated in a local-to-global order, it is by no means clear that it is completed in this order. Indeed, there is strong evidence that the flow of neural information processing is not unidirectional from the sensory surface of the retina to higher centers of the brain. Massive backward projections from higher to lower cortical areas suggest that a great deal of feedback may occur, although nobody yet knows precisely what form it takes or even what functions it serves. The existence of feedback raises the possibility that the order in which perceptual experience arises is not given by the simplistic reading of the physiological facts given in the previous paragraph. Moreover, evidence from psychological experiments suggests that perception of global objects often precedes that of local parts.

Global Precedence

Navon (1976) asked about the priority of wholes versus parts by studying discrimination tasks with hierarchically structured stimuli: typically, large letters made of many appropriately positioned small letters. On some trials subjects were shown consistent configurations in which the global and local letters were the same, such as a large H made of many small Hs or a large S made of many small Ss. On others, they were shown inconsistent configurations in which the global and local letters conflicted, such as a large H made of many small Ss or a large S made of many small Hs. They were cued on each trial whether to report the identity of the letter represented at the global or the local level. Response times and error rates were measured.

The results of Navon’s experiment strongly supported the predictions of global precedence: the hypothesis that observers perceive the global level of hierarchical stimuli before the local level. Response times were faster to global than to local letters, and global inconsistency interfered when subjects were attending to the local level, but local inconsistency did not interfere when they were attending to the global level. The data thus appear to indicate that perceptual processes proceed from global, coarse-grained analysis to local, finegrained analysis.

Further investigation suggested a more complex story, however. Kinchla and Wolfe (1979) found that the speed of naming local versus global forms depended on their retinal sizes. Identifying global letters was faster than local ones when the global stimuli were smaller than about 8–10° of visual angle, but identifying local letters was faster than global ones when the stimuli were larger than this. Other experiments suggest that global and local levels of information are being processed simultaneously rather than sequentially. For example,when subjects were monitoring for a target letter at either the global or the local levels, their responses were faster when a target letter was present at both global and local levels than when there was a target letter present at either level alone (Miller, 1981). The findings on global versus local precedence may therefore be best understood as the resultofparallelprocessingindifferentsizechannels,withsome channels being processed slightly faster than others, rather than as reflecting a fixed global-to-local order of processing.

Further experiments by Robertson and her colleagues studying patients with brain damage have shown that global and local information is processed differently in the two cerebral hemispheres. Several lines of evidence show that there is an advantage for global processing in the right temporalparietal lobe, whereas there is an advantage for local processing in the left temporal-parietal lobe (Robertson, Lamb, & Knight, 1988). For example, Figure 7.16 shows how patients with lesions in the left versus right temporal-parietal region copied the hierarchical stimulus shown on the left in part A (Delis, Robertson, & Efron, 1986). The patient with right hemisphere damage, who suffers deficits in global processing, is able to reproduce the small letters making up the global letter, but is unable to reproduce their global structure. The patient with left hemisphere damage, who suffers deficits in local processing, is able to reproduce the global letter, but not the small letters that comprise it.

Further psychological evidence that global properties are primary in human perception comes from experiments in whichdiscriminationofpartsisfoundtobesuperiorwhenthey are embedded within meaningful or well-structured wholes. Not only is performance better than in comparable control conditions in which the same parts must be discriminated within meaningless or ill-structured contexts, but it is also superior compared to discriminating the same parts in isolation. This evidence comes from several different phenomena, such asthewordsuperiorityeffect(Reicher,1969),theobjectsuperiority effect (Weisstein & Harris, 1974), the configural orientation effect (Palmer, 1980; Palmer & Bucher, 1981), and the configural superiority effect (Pomerantz, Sager, & Stover, 1977).Although space limitations do not permit discussion of these interesting experiments, their results generally indicate that perceptual performance on various simple local discrimination tasks does not occur in the local-to-global order.

Exactly how these contextual effects should be interpreted is open to debate, however. One possibility is that neural processing proceeds from local parts to global wholes, but feedback from the holistic level to the earlier part levels then facilitates processing of local elements, if they are part of coherent patterns at the global level. This is the mechanism proposed in the influential interactive activation model of letter and word processing (McClelland & Rumelhart, 1981; Rumelhart & McClelland, 1982). Another possibility is that although neural processing proceeds from local parts to global wholes, people may gain conscious access to the results in the opposite order, from global wholes to local parts (Marcel, 1983). Regardless of what mechanism is ultimately found to be responsible, the results of many psychological experiments rule out the possibility that the perception of local structure necessarily precedes that of global structure. The truth, as usual, is much more interesting and complex.

Frames of Reference

Another set of perceptual phenomena that support the priority of global, large-scale structure in perceptual organization is the existence of what are called reference frame effects (see Rock, 1990, for a review). Aframe of reference in visual perception is a set of assumed reference standards with respect to which the properties of perceptual objects are encoded. Visual reference frames are often considered to be analogous to coordinate systems in analytic geometry (Palmer, 1989). Reference frame effects generally show that the reference frame for a given visual element is defined by the next-higher element in the perceptual part-whole hierarchy. In this section, reference frame effects in orientation and shape perception are briefly considered. Analogous effects are also present in motion perception.

Orientation Perception

One of the most compelling demonstrations of reference frame effects on orientation perception occurs when you enter a tilted room, like the ones in a fun house or mystery house of an amusement park. Although you notice the slant of the floor as you first enter, you rapidly come to perceive the room as gravitationally upright. After this misperception occurs, all sorts of other illusions follow. You perceive the chandelier as hanging at a strange angle from the ceiling, for example, and you perceive yourself as leaning precariously to one side, despite the fact that both the chandelier and you are, in fact, gravitationally upright. If you try to correct your posture to align yourself with the orientation of the room, you may lose your balance or even fall.

Normally, the vertical orientation in the reference frame of the large-scale visual environment coincides with gravitational vertical, because the dominant orientations of perceived objects—due to walls, floors, tree trunks, the ground plane, standing people, and so forth—are either aligned with gravity or perpendicular to it. The heuristic assumption that the walls, floor, and ceiling of a room are vertical and horizontal thus generally serves us well in accurately perceiving the orientations of objects. When you walk into a tilted room, however, this assumption is violated, giving rise to illusions of orientation. The visual reference frame of the room, which is out of alignment with gravity, captures your sense of upright. You then perceive yourself as tilted because your own bodily orientation is not aligned with your perception of upright.

One particularly well-known reference frame effect on orientation perception is the rod and frame effect (Asch & Witkin, 1948a, 1948b). Subjects were shown a luminous rod within a large, tilted, luminous rectangle and were asked to set the rod to gravitational vertical. Asch and Witkin found large systematic errors in which subjects set the rod to an orientation somewhere between true vertical and alignment with the frame’s most nearly vertical sides. Several experiments show that the effect of the frame is greatest when the rectangle is large, and that small ones just surrounding the line have little effect (Ebenholtz, 1977; Wenderoth, 1974).

Other studies have shown that when two frames are present, one inside the other, it is the larger surrounding frame that dominates perception (DiLorenzo & Rock, 1982). These facts are consistent with the interpretation that the rectangle in a rod and frame task induces a visual frame of reference that is essentially a world surrogate, so to speak, for the visual environment (Rock, 1990). By this account, a visual structure will be more likely to induce a frame of reference when it is large, surrounding, and stable over time, like the tilted room in the previous example.

Shape Perception

Because perceived shape depends on perceived orientation, robust reference frame effects also occur in shape perception. One of the earliest, simplest, and most elegant demonstrations of this fact was Mach’s (1914/1959) observation that when a square is rotated 45°, people generally perceive it as an upright diamond rather than as a tilted square. This figure can be perceived as a tilted square if the flat side at 45° is taken to be its top. But if the upper vertex is perceived as the top, the shape of the figure is seen as diamond-like and quite different from that of an upright square.

This relation suggests that the shape of an object should also be influenced by the orientation of a frame of reference, and this is indeed true. One of the earliest and most compelling demonstrations was provided by Kopferman (1930), who showed that a gravitational diamond is perceived as a square when it is enclosed within a 45° tilted rectangle. Palmer (1985) later extended Kopferman’s discovery to other factors that Palmer had previously shown to influence orientation perception in the perceived pointing of ambiguous, equilateral triangles, factors such as the orientation of configural lines, the width and orientation of textural stripes, and the direction of rigid motion (Palmer & Bucher, 1982; Bucher & Palmer, 1985). In all of these cases, the claim is that the contextual factors induce a perceptual frame of reference that is aligned along the 45° axis of the diamond and that the shape of the figure is then perceived relative to that orientation, leading to the perception of a tilted square rather than an upright diamond.

Rock (1973) showed that such reference frame effects on shape perception are much more general. He presented subjects with a sequence of amorphous, novel shapes in a particular orientation during an initial presentation phase. He later tested their recognition memory for the figures in the same versus a different orientation (see Figure 7.17; A). The results showed that people were far less likely to recognize the shapes if they were tested in an orientation different from the original one. This poor recognition performance, which approached chance for 90° rotations, indicates that subjects often fail to perceive the equivalence in shape of the presented and tested figures when they are differently oriented. Further, Rock (1973) found that tilting the observer’s head reduced recognition memory less than tilting the objects within the environment. This suggests that the reference frames for these figures are environmental rather than retinal.

Why, then, do people seldom fail to recognize, say, a chair when it is seen lying on its side rather than standing up? The crucial fact appears to be that objects like chairs have enough orientational structure that they effectively carry their own intrinsic, object-centered reference frames along with them. Roughly speaking, an object-centered reference frame is a perceptual reference frame that is chosen on the basis of the intrinsic properties of the to-be-described object, one that is somehow made to order for that particular object (see Palmer, 1999, pp. 368–371). For example, if the orientations of two otherwise identical objects are different, such as an upright and a tipped-over chair, the orientation of each object-centered reference frame—for instance, the axis of elongation that lies in its plane of symmetry—will be defined such that both objects will have the same shape description relative to their object-centered frames.

Wiser (1981) used Rock’s memory paradigm to study shape perception for objects with good intrinsic axes and found that they are recognized as well when they are presented and tested in different orientations as when they are presented and tested in the same orientation (Figure 7.17; B). In further experiments, she showed that when a wellstructured figure is presented initially so that its axis is not aligned with gravitational vertical, subsequent recognition is actually fastest when the figure is tested in its vertical orientation. She interpreted this result to mean that the shape is stored in memory as though it were upright, relative to its own object-centered reference frame.

Object Identification

After the image has been organized into a part-whole hierarchy and partly hidden surfaces have been completed, the perceptual objects thus defined are very often identified as instances of known, meaningful types, such as people, houses, trees, and cars. This process of object identification is often also referred to as object recognition or object categorization. Its presumed goal is the perception of function, thereby enabling the observer to know, simply by looking, what objects in the environment are useful for what purposes. The general idea behind perceiving function via object identification is to match the perceived properties of a seen object against internal representations of the properties of known categories of objects. After the object has been identified, its function can then be determined by retrieving associations between the object category and its known uses. This will not make novel uses of the object available—additional problem solving processes are required for that purpose—rather, only uses that have been previously understood and stored with that category are retrieved.

Before pursuing the topic of object identification in depth, it is worth mentioning that there is an alternative approach to perceiving function. The competing view is Gibson’s (1979) theory of affordances, in which opportunities for action are claimed to be perceived directly from visible structure in the dynamic optic array. Gibson claimed, for example, that people can literally see whether an object affords being grasped, or sat upon, or walked upon, or used for cutting without first identifying it as, say, a baseball, a chair, a floor, or a knife. This is possible only if the relation between an object’s form and its affordance (the function it offers the organism) is transparent enough that the relevant properties are actually visible. If this is not the case, then category-mediated object identification appears to be the only route for perception of function.

Typicality and Basic-Level Categories

The first fact that must be considered about identifying objects is that it is an act of classification or categorization. Although most people typically think of objects as belonging to just one category—something is either a dog, a house, a tree, or a book—all objects are actually members of many categories. Lassie is a dog, but she is also a collie, a mammal, an animal, a living thing, a pet, a TV star, and so on. The categories of human perception and cognition are quite complex and interesting psychological structures.

One of the most important modern discoveries about human categorization is the fact that our mental categories do not seem to be defined by sets of necessary and sufficient conditions, but rather to be structured around so-called best examples, called prototypes (Rosch, 1973, 1975a, 1975b). The prototypical bird, for example, would be the “birdiest” possible bird: probably a standard bird that is average in size, has a standard neutral sort of coloring, and has the usual shape of a bird. When Rosch asked participants to rate various members of a category, like particular kinds of birds, in terms of how “good” or “typical” they were as examples of birds, she found that they systematically rated robins quite high and penguins and ostriches quite low. These typicality (or goodness-of-example) ratings turn out to be good predictors of how quickly subjects can respond “true” or “false” to verbal statements such as, “A robin is a bird,” versus, “A penguin is a bird” (Rosch, 1975b). Later studies showed that it also takes longer to verify that a picture of a penguin depicts an example of a bird than to verify that a picture of a robin does (Ober-Thomkins, 1982). Thus, the time required to identify an object as a member of a category depends on how typical it is perceived to be as an example of that category.

Rosch’s other major discovery about the structure of human categories concerned differences among levels within the hierarchy. For example, at which level does visual identification first occur: at some low, specific level (e.g., collie), at some high, general level (e.g., animal), or at some intermediate level (e.g., dog)? The answer is that people generally recognize objects first at an intermediate level in the categorical hierarchy. Rosch called categories at this level of abstraction basic level categories (Rosch, Mervis, Gray, Johnson, & Boyes-Braem, 1976). Later research, however, has shown the matter to be somewhat more complex.

Jolicoeur, Gluck, and Kosslyn (1984) studied this issue by having subjects name a wide variety of pictures with the first verbal label that came to mind. They found that objects that were typical instances of categories, such as robins or sparrows, were indeed identified as members of a basic level category, such as birds. Atypical ones, such as penguins and ostriches, tended to be classified at a lower, subordinate level. This pattern of naming was not universal for all atypical category members, however. It occurs mainly for members of basic level categories that are relatively diverse. Consider some basic level categories from the superordinate categories offruit(e.g.,apples,bananas,andgrapes)versusanimals(e.g., dogs, birds, and monkeys). Most people would agree that the shape variation within the categories of apples, for instance, is more constrained than that within the categories of dogs. Indeed, most people would be hard-pressed to distinguish between two different kinds of apples, bananas, or grapes from shape alone, but consider how different dachshunds are from greyhounds, penguins are from ostriches, and goldfish are from sharks. Not surprisingly, then, the atypical exemplars from diverse basic-level categories are the ones that tend to be named according to their subordinate category. Because the categories into which objects are initially classified is sometimes different from the basic level, Jolicoeur, Gluck, and Kosslyn (1984) called them entry-level categories.

It is worth noting that, as in the case of basic-level categories, the entry-level category of an object can vary over different observers, and perhaps over different contexts as well. To an ornithologist or even to an avid bird watcher, for instance, bird may be the entry-level category for very few, if any, species of bird. Through a lifetime of experience at discriminating different kinds of birds, their perceptual systems may become so finely tuned to the distinctive characteristics of different kinds of birds that they first perceive robins as robins and sparrows as sparrows rather than just as birds (Tanaka & Taylor, 1991).

Perspective Effects

One of the seemingly obvious facts about identifying threedimensional objects is that people can do it from almost any viewpoint. The living-room chair, for example, seems to be easily perceived as such regardless of whether one is looking at it from the front, side, back, top, or any combination of these views. Thus, one of the important phenomena that must be explained by any theory of object classification is how this is possible.

But given the fact that object categorization is possible from various perspective views, it is all too easy to jump to the conclusion that object categorization is invariant over perspective views. Closer study indicates that this is not true. Palmer, Rosch, and Chase (1981) systematically investigated and documented perspective effects in object identification. They began by having participants view many pictures of the same object (such as the horse series in Figure 7.18) and make subjective ratings of how much each one looked like the objects they depicted using a scale from 1 (very like) to 7 (very unlike). Participants made the average ratings indicated below the pictures. Other individuals were then asked to name the entry-level categories of these pictures, as quickly as possible, using five perspectives (from the best to the worst) based on the ratings. Pictures rated as the best (or canonical) perspective were named fastest, and naming latencies gradually increased as the goodness of the views declined, with the worst ones being named much more slowly than the best ones.

It seems possible that such perspective effects could be explained by familiarity: Perhaps canonical views are simply the most frequently seen views. More recent studies have examined perspective effects using identification of novel objects to control for frequency effects. For example, Edelman and Bülthoff (1992) found canonical view effects in recognition time for novel bent paper-clip objects that were initially presented to subjects in a sequence of static views that produced apparent rotation of the object in depth (Figure 7.19). Because each single view was presented exactly once in this motion sequence, familiarity effects should be eliminated. Even so, recognition performance varied significantly over viewpoints, consistent with the perspective effects reported by Palmer et al. (1981).

Further studies have shown that familiarity does matter, however. When only a small subset of views was displayed in the initial training sequence, later recognition performance was best for the views seen during the training sequence and decreased with angular distance from these training views (Bülthoff & Edelman, 1992; Edelman & Bülthoff, 1992). These results suggest that subjects may be storing specific two-dimensional views of the objects and matching novel views to them via processes that deteriorate with increasing disparity between the novel and stored views.

Further experiments demonstrated that when multiple views of the same objects were used in the training session, recognition performance improved, but the improvement depended on the relation of the test views to the training views (Bülthoff & Edelman, 1992). In particular, if the novel test views were related to the training views by rotation about the same axis through which the training views were related to each other, recognition was significantly better than for novel views that were rotations about an orthogonal axis. This suggests that people may be interpolating between and extrapolating beyond specific two-dimensional views in recognizing three-dimensional objects. This possibility will be important in this research paper’s section entitled “Theories of Object Identification,” in which view-based theories of object categorization are described (e.g., Poggio & Edelman, 1990; Ullman, 1996; Ullman & Basri, 1991).

A different method of study, known as the priming paradigm, has produced interesting but contradictory results about perspective views. The basic idea behind this experimental design is that categorizing a particular picture of an object will be faster and more accurate if the same picture is presented a second time, because the processes that accomplish it initially are in a state of heightened readiness for the second presentation (Bartram, 1974). The priming effect is defined as the difference between the naming latencies in the first block of trials and those in the second block of repeated pictures. What makes priming experiments informative about object categorization is that the repetitions in the second block of trials can differ from the initial presentation in different ways. For example, repetitions can be of the same object, but with changes in its position within the visual field (e.g., left vs. right side), its retinal size (large vs. small), its mirror-image reflection (as presented initially or left-right reversed), or the perspective from which the object is viewed.

The results of such studies show that the magnitude of the object priming effect does not diminish when the second presentation shows the same object in a different position or reflection (Biederman & Cooper, 1991) or even at a different size (Biederman & Cooper, 1992). Showing the same object from a different perspective, however, has been found to reduce the amount of priming (Bartram, 1974). This perspective effect is thus consistent with the naming latency results reported by Palmer et al. (1981) and the recognition results by Edelman and Bülthoff (1992) and Bülthoff and Edelman (1992). Later studies on priming with different perspective views of the same object by Biederman and Gerhardstein (1993), however, failed to show any significant decrease in priming effects due to depth rotations.

To explain this apparent contradiction, Biederman and Gerhardstein (1993) then went on to show that priming effects did not diminish when the same parts were visible in the different perspective conditions. This same-part visibility condition is not necessarily met by the views used in the other studies, which often include examples in which different parts were visible from different perspectives (see Figure 7.18). Visibility of the same versus different parts may thus explain why perspective effects have been found in some priming experiments but not in others. The results of these experiments on perspective effects therefore suggest care in distinguishing two different kinds of changes in perspective: those that do not change the set of visible parts, and those that do.

Orientation Effects

Other effects due to differences in object orientation cannot be explained in this way, however, because the same parts are visible in all cases. Orientation effects refer to perceptual differences caused by rotating an object about the observer’s line of sight rather than rotating it in depth. Depth rotations of the object often change the visibility of different parts of the object, as just discussed, but orientation changes never do, and Jolicoeur (1985) has shown that subjects are faster at categorizing pictures of objects in a normal, upright orientation than when they are misoriented in the picture plane. Naming latencies increase with angular deviation from their upright orientation, as though subjects were mentally rotating the objects to upright before making their response.

Interestingly, orientation effects diminish considerably with extended practice. Tarr and Pinker (1989) studied this effect using novel objects so that the particular orientations at which subjects saw the objects could be precisely controlled. When subjects received extensive practice with the objects at several orientations, rather than just one, naming latencies were fast at all the learned orientations. Moreover, response times at novel orientations increased with distance from the nearest familiar orientation. Tarr and Pinker therefore suggested that people may actually store multiple representations of the same object at different orientations rather than a single representation that is orientation invariant. This possibility becomes particularly important in the section entitiled “Theories of Object Identification,” in which view-specific theories of categorization are considered.

Part Structural Effects

The first half of this research paper developed the idea that perceptual organization is centrally related to the idea that the perceived world is structured into part-whole hierarchies. Human bodies have heads, arms, legs, and a torso; tables have a flat top surface, and legs; an airplane has a fuselage, two main wings, and several smaller tail fins. The important question is whether these parts play a significant mediating role in object identification. The most revealing studies of this question were performed by Biederman and Cooper (1991) using a version of the priming paradigm discussed in this research paper’s section entitled “Perspective Effects.” They showed that identification of degraded line drawings in the second (test) block of trials was facilitated when subjects had seen the same parts of the same objects in the initial (priming) block, but not when they had seen different parts of the same object in the priming block. This result implies that the process of identifying objects is mediated by perceiving their parts and spatial interrelations—because otherwise, it is not clear why more priming occurs only when the same parts were seen again.

The drawings Biederman and Cooper (1991) used were degraded by deleting half of the contours in each stimulus. In the first experiment, subjects were shown a priming series of contour-deleted drawings and then a test series in which they saw either the identical drawing (Figure 7.20; A), its line complement (Figure 7.20; B), or a different object from the same category (Figure 7.20; C). The results showed that the line-complement drawings produced just as much priming (170 ms) as the identical drawings (168 ms), and much more than the same-name drawings (93 ms). Biederman and Cooper (1991) argued that the stronger priming in the first two conditions was due to the fact that the same parts were perceived both in the identical and the line-complement drawings.

To be sure that this pattern was not due merely to the fact that the same object was depicted in the same pose in both of these conditions, they performed a second experiment, in which half of the parts were deleted in the initial priming block (Figures 7.21; A–C). Then, in the test block, they found that priming by the part-complement drawings was much less (108 ms) than was priming by the identical drawings (190 ms). In fact, part-complement priming was no different from that in the same-name control condition (110 ms). Thus, the important feature for obtaining significantly more priming than for mere response repetition is that the same parts must be visible in the priming and test blocks. This result supports the inference that object identification is mediated by part perception.

Contextual Effects

All of the phenomena of object identification considered thus far concern the nature of the target object itself: how typical it is of its category, the perspective from which it is viewed, and its size, position, orientation, and visible parts. But identification can also be influenced by contextual factors: the spatial array of objects that surround the target object. One wellknown contextual effect can be demonstrated by the phrase , which everyone initially perceives as THE CAT. This seems entirely unproblematic—until one realizes that the central letters of both words are actually identical and ambiguous, midway between an H and an A. It is therefore possible that the letter strings could be perceived as TAE CHT, TAE CAT, or THE CHT, but this almost never happens.

There have been several well-controlled experiments documenting that appropriate context facilitates identification, whereas inappropriate context hinders it. In one such study, Palmer (1975a) presented subjects with line drawings of common objects to be identified following brief presentations of contextual scenes (Figure 7.22). The relation between the contextual scene and the target object was studied. In the case of the kitchen counter scene, for example, the subsequently presented object could be either appropriate to the scene (a loaf of bread), inappropriate (a bass drum), or misleading in the sense that the target object was visually similar to the appropriate object (a mailbox). For the no-context control condition, the objects were presented following a blank field instead of a contextual scene. By presenting the objects and scenes in different combinations, all objects were equally represented in all four contextual conditions.

The results of this experiment showed that appropriate contexts facilitated correct categorization relative to the nocontext control condition and that inappropriate contexts inhibited it. Performance was worst of all in the misleading context condition, in which participants were likely to name the visually similar object appropriate to the scene. These differences demonstrate that recognition accuracy can be substantially affected by the nature of the surrounding objects in a simple identification task.

Biederman (1972; Biederman, Glass, & Stacy, 1973) used a different method to study context effects. He had participants search for the presence of a given target object in a scene and measured their visual search times. In the first study, he manipulated context by presenting either a normal photograph or a randomly rearranged version. Participants took substantially longer to find the target object in the rearranged pictures than in the normal ones.

These contextual effects indicate that relations among objects in a scene are complex and important factors for normal visual identification. Obviously, people can identify objects correctly even in bizarre contexts. A fire hydrant on top of a mailbox may take longer to identify—and cause a major double-take after it is identified—but people manage to recognize it even so. Rather, context appears to change the efficiency of identification. In each case, the target object in a normal context is processed quickly and with few errors, whereas one in an abnormal context takes longer to process and is more likely to produce errors. Because normal situations are, by definition, encountered more frequently than are abnormal ones, such contextual effects are generally beneficial to the organism in its usual environment.

Visual Agnosia

A very different—and fascinating phenomenon of object identification is visual agnosia, a perceptual deficit due to brain damage, usually in the temporal lobe of cortex, in which patients are unable to correctly categorize common objects with which they were previously familiar. (Agnosia is a term derived from Greek that means not knowing.) There are many different forms of visual agnosia, and the relations among them are not well understood. Some appear to be primarily due to damage to the later stages of sensory processing (termed apperceptive agnosia by Lissauer, 1890/1988). Such patients appear unable to recognize objects because they do not see them normally. Other patients have fully intact perceptual abilities, yet still cannot identify the objects they see, a condition Lissauer called associative agnosia. Teuber (1968) described their condition as involving “a normal percept stripped of its meaning” due to an inability to categorize it correctly.

The case of a patient, known as “GL,” is a good example of associative agnosia (Ellis & Young, 1988). This patient suffered a blow to his head when he was 80 years old, after which he complained that he could not see as well as before the accident. The problem was not that he was blind or even impaired in basic visual function, for he could see the physical properties of objects quite well; indeed, he could even copy pictures of objects that he could not identify. He mistook pictures for boxes, his jacket for a pair of trousers, and generally could not categorize even the simplest everyday objects correctly.

Patients with visual agnosia suffer from a variety of different symptoms. Some have deficits specific to particular classes of objects or properties. One classic example is prosopagnosia: the inability to recognize faces. Prosopagnosic patients can describe in detail the facial features of someone at whom they are looking, yet be completely unable to recognize the person, even if it is their spouse, their child, or their own face in a mirror. Such patients will typically react to a relative as a complete stranger—until the person speaks, at which time the patient can recognize his or her voice.

Other agnosic patients have been studied who have problems with object categories such as living things. Patient JBR, for example, was able to identify 90% of the pictures depicting inanimate objects, but only 6% of those depicting plants and animals (Warrington & Shallice, 1984). Even more selective deficits have been reported, including those confined to body parts, objects found indoors, and fruits and vegetables, although some of these deficits may be linguistic in nature rather than perceptual (Farah, 1990).

One problem for many visual agnosic persons that has been studied experimentally is their particular inability to categorize objects presented in atypical or unusual perspective views. Warrington and Taylor (1973, 1978) found that many agnosic persons who are able to categorize pictures of common objects taken from a usual perspective are unable to do so for unusual views. This phenomenon in agnosic patients bears a striking resemblance to perspective effects found in normally functioning individuals (Palmer et al., 1981), except that instead of simply taking longer to arrive at the correct answer, these patients are unable to perform the task at all, even in unrestricted viewing conditions.

There are many other visual disorders due to brain damage that are related to visual agnosia. They exhibit a wide variety of complex symptoms, are caused by a broad range of underlying brain pathologies, and are generally not well understood. Still, the case histories of such patients and their phenomenological descriptions of their symptoms make for fascinating reading, such as the patient whose agnosia led neurologist Oliver Sacks (1985) to entitle one of his books, The Man Who Mistook His Wife for a Hat. The interested reader is referred to Farah (1990, 2000) for discussions of these and related disorders.

Theories of Object Identification

Given that people obviously manage to identify visually perceived objects as members of known, functional classes, how might this result be achieved? There are many possibilities, but within a modern, computational framework, all of them require four basic components: (a) The relevant characteristics of the to-be-categorized object must be perceived and represented within the visual system in an object representation; (b) Each of the set of possible categories must be represented in memory in a category representation that is accessible to the visual system; (c) There must be comparison processes through which the object representation is matched against possible category representations; (d) There must be a decision process that uses the results of the comparison process to determine the category to which a given object belongs. This section considers each of these components and then describes two contrasting types of theories that attempt to explain how object identification might be performed.

Representing Objects and Categories

The problem of how to represent objects and categories is a difficult one (cf. Palmer, 1978) that lies at the heart of most theories of object identification. Especially thorny are the representational issues pertaining to shape, which tends to be the single most important feature for object identification. Most proposals about shape representation cluster into three general classes: templates, feature lists, and structural descriptions, although various hybrids are also possible. Space limitations prohibit a detailed discussion of these issues, but the interested reader can consult the more extensive treatment by Palmer (1999).

Templates

The idea behind templates is to represent shape as shape. In standard presentations of this kind of theory, templates are specifiedbytheconjunctionofthesetofreceptorsonwhichthe image of the target shape would fall. A template for a square, for example, can be formed by constructing what is called a square-detector cell whose receptive field structure consists of excitation by all receptors that the square would stimulate, plus inhibition by all nearby receptors around it that it would not stimulate (Figure 7.23). A white square on a black ground would maximally excite this square detector because its spatial structure corresponds optimally to that of its receptive field.

Templates are often ridiculed as grossly inadequate for representing shape. In fact, however, they are the most obvious way to convert spatially structured images into symbolic descriptions. Line- and edge-detector theories of simple cells in cortical area V1 can be viewed as template representations for lines and edges. Each line detector cell responds maximally to a line at a specific position, orientation, and contrast (light on dark versus dark on light). Whether such a scheme can be extended to more complex shape representations is questionable (see following discussion), but recent theories of object identification have concentrated on view-specific representations that are template-like in many respects (see this research paper’s section entitled “View-Specific Theories”).

Some of the most difficult problems associated with templates as a general scheme for representing shapes of objects and categories are outlined in the following list:

1. Concreteness: There are many visual factors that have essentially no impact on perceived shape, yet strongly influence the matching of template representations, including factors such as differences in lightness, color, texture, binocular disparity, and other low-level sensory features. A green square on a yellow ground is seen as having the same shape as a blue square on a red ground, for example, even though they will require separate templates. A general square template would thus have to be the disjunction of a huge number of very specific square templates.

2. Spatial transformations: Shape is largely invariant over the similarity transformations—translations, rotations, dilations, reflections, and their various combinations (Palmer, 1989)—yet comparing template representations that differ by such transformations will not generally produce good matches. Three ways to solve this problem for template representations are replication, interpolation, and normalization. Replication refers to the strategy of constructing a different template for each distinct shape in each position, orientation, size, and sense (reflection), as the visual system does for receptive field structures in area V1. This is feasible only if the set of template shapes is very small, however. Interpolation is a way of reducing the number of templates by including processes that can construct intermediate representations between a pair of stored templates, thus reducing the number of templates, but at the expense of increasing the complexity of the matching process. Normalization postulates processes that transform (or normalize) the input image into a canonical position,orientation, size, and sense prior to being matched against the templates so that these factors do not matter. How to normalize effectively then becomes a further problem.
3. Part structure: People perceive most objects as having a complex hierarchical structure of parts (see this research paper’s section entitled “Perceptual Organization”), but templates have just two levels: the whole template and the atomic elements (receptors) that are associated within the template. This means that standard templates cannot be matched on a partwise basis, as appears to be required when an object is partly occluded.
4. Three dimensionality: Templates are intrinsically twodimensional, whereas most objects are three-dimensional. There are just two solutions to this problem. One is to make the internal templates three-dimensional, like the objects themselves, but that means that three-dimensional templates would have to be constructed by some complex process that integrates many different two-dimensional views into a single three-dimensional representation (e.g., Lowe, 1985). The other solution is to make the internal representations of three-dimensional objects twodimensional by representing two-dimensional projections of their shapes. This approach has the further problem that different views of the same object would then fail to match any single template. Solving this problem by replication requires different templates for each distinct perspective view, necessitating hundreds or thousands of templates for complex three-dimensional objects. Solving it by interpolation requires additional processes that generate intermediate views from two stored views (e.g., Poggio & Edelman, 1990; Ullman & Basri, 1991). Normalization is not feasible because a single two-dimensional view simply does not contain enough information to specify most objects from some other viewpoint.

Feature Lists

A more intuitively appealing class of shape representation is feature lists: symbolic descriptions consisting of a simple set of attributes. A square, for example, might be represented by the following set of discrete features: is-closed, has-foursides, has-four-right-angles, is-vertically-symmetrical, ishorizontally-symmetrical, etc. The degree of similarity between an object shape and that of a stored category can then be measured by the degree of correspondence between the two feature sets.

In general, two types of features have been used for representing shape: global properties, such as symmetry, closure, and connectedness, and local parts, such as containing a straight line, a curved line, or an acute angle. Both types of properties can be represented either as binary features (e.g., a given symmetry being either present or absent) or as continuous dimensions (e.g., the degree to which a given symmetry is present). Most classical feature representations are of the discrete, binary sort (e.g., Gibson, 1969), but ones based on continuous, multidimensional features have also been proposed (e.g., Massaro & Hary, 1986).

One reason for the popularity of feature representations is that they do not fall prey to many of theo bjections that so cripple template theories. Feature representations can solve the problem of concreteness simply by postulating features that are already abstract and symbolic. The feature list suggested for a square at the beginning of this section, for example, made no reference to its color, texture, position, or size. It is an abstract, symbolic description of all kinds of squares. Features also seem able to solve the problem of part structure simply by including the different parts of an object in the feature list, as in the previously mentioned feature list for squares. Similarly, a feature representation of a human body might include the following part-based features: having-a-head, having-atorso, having-two-legs, and so forth. The features of a head would likewise include having two-eyes, having-a-nose, having-a-mouth, etc. Features also seem capable of solving the problems resulting from three-dimensionality, at least in principle. The kinds of features that are included in a shape representation can refer to intrinsically three-dimensional qualities and parts as well as two-dimensional ones, and so can be used to capture the shape of three-dimensional as well as two-dimensional objects. For instance, the shape of an object can be described as having the feature spherical rather than circular and as contains-a-pyramid rather than containsa-triangle. Thus, there is nothing intrinsic to the feature-list approach that limits it to two-dimensional features.

Feature theories have several important weaknesses, however. One is that it is often unclear how to determine computationally whether a given object actually has the features that are proposed to comprise its shape representation. Simple part-features of two-dimensional images, such as lines, edges, and blobs, can be computed from an underlying template system as discussed above, but even these must be abstracted from the color-, size-, and orientation-specific peripheral channels that detect lines, edges, and blobs. Unfortunately, these simple image-based features are just the tip of a very large iceberg. They do not cover the plethora of different attributes that feature theorists might (and do) propose in their representations of shape. Features like contains-acylinder or has-a-nose, for instance, are not easy to compute from gray-scale images. Until such feature-extraction routines are available to back up the features proposed for the representations, feature-based theories are incomplete in a very important sense.

Another difficult problem is specifying what the proper features might be for a shape representation system. It is one thing to propose that some appropriate set of shape features can, in principle, account for shape perception, but quite another to say exactly what those features are. Computer-based methods such as multidimensional scaling (Shepard, 1962a, 1962b) and hierarchical clustering can help in limited domains, but they have not yet succeeded in suggesting viable schemes for the general problem of representing shape in terms of lists of properties.

Structural Descriptions

Structural descriptions are graph-theoretical representations that can be considered an elaboration or extension of feature theories. They generally contain three distinct types of information: properties, parts, and relations between parts. They are usually depicted as hierarchical networks in which nodes represent the whole object and its various parts and subparts with labeled links (or arcs) between nodes that represent structural relations between objects and parts. Because of this hierarchical network format, structural descriptions are surely the representational approach that is closest to the view of perceptual organization that was presented in the first half of this research paper.

Another important aspect of perceptual organization that can be encoded in structural descriptions is information about the intrinsic reference frame for the object as a whole and for each of its parts. Each reference frame can be represented as global features attached to the node corresponding to the object or part, one each for its position, orientation, size, and reflection (e.g., Marr, 1982; Palmer, 1975b). The reference frame for a part can then be represented relative to that of its superordinate, as evidence from organizational phenomena suggests (see this research paper’s section entitled “Frames of Reference”).

One serious problem with structural descriptions is how to represent the global shapes of the components. An attractive solution is to postulate shape primitives: a set of indivisible perceptual units into which all other shapes can be decomposed. For three-dimensional objects, such as people, houses, trees, and cars, the shape primitives presumably must be three-dimensional volumes. The best known proposal of this type is Binford’s (1971) suggestion, later popularized by Marr (1982), that complex shapes can be analyzed into combinations of generalized cylinders. As the name implies, generalized cylinders are a generalization of standard geometric cylinders in which several further parameters are introduced to encompass a larger set of shapes. Variables are added to allow, for example, a variable base shape (e.g., square or trapezoidal in addition to circular), a variable axis (e.g., curved in addition to straight), a variable sweeping rule (e.g., the cross-sectional size getting small toward one end in addition to staying a constant size), and so forth. Some of the other proposals about shape primitives are very closely related to generalized cylinders, such as geons (Biederman, 1987) and some are rather different, such as superquadrics (Pentland, 1986).

Structural descriptions with volumetric shape primitives can overcome many of the difficulties with template and feature approaches. Like features, they can represent abstract visual information, such as edges defined by luminance, texture, and motion. They can account for the effects of spatial transformations on shape perception by absorbing them within object-centered reference frames. They deal explicitly with the problem of part structure by having distinct representations of parts and the spatial relations among those parts. And they are able to represent three-dimensional shape by using volumetric primitives and three-dimensional spatial relations in representing three-dimensional objects.

One difficulty with structural descriptions is that the representations become quite complex, so that matching two such descriptions constitutes a difficult problem by itself. Another is that a sufficiently powerful set of primitives and relations must be identified. Given the subtlety of many shapedependent perceptions, such as recognizing known faces, this is not an easy task. Further, computational routines must be devised to identify the volumetric primitives and relations from which the structural descriptions are constructed, whatever those might be. Despite these problems, structural descriptions seem to be in the right ballpark, and their general form corresponds nicely with the result of organizational processes discussed in the first section of this research paper.

Comparison and Decision Processes

After a representation has been specified for the to-beidentified objects and the set of known categories, a process has to be devised for comparing the object representation with each category representation. This could be done serially across categories, but it makes much more sense for it to be performed in parallel. Parallel matching could be implemented, for example, in a neural network that works by spreading activation, where the input automatically activates all possible categorical representations to different degrees, depending on the strength of the match (e.g., Hummel & Biederman, 1992).

Because the schemes for comparing representations are rather specific to the type of representation, in the following discussion I will simply assume that a parallel comparison process can be defined that has an output for each category that is effectively a bounded, continuous variable representing how well the target object’s representation matches the category representation. The final process is then to make a decision about the category to which the target object belongs. Several different rules have been devised to perform this decision, including the threshold, best-fit, and bestfit-over-threshold rules.

The threshold approach is to set a criterial value for each category that determines whether a target object counts as one of its members. The currently processed object is then assigned to whatever category, if any, exceeds its threshold matching value. This scheme can be implemented in a neural network in which each neural unit that represents a category has its own internal threshold, such that it begins to fire only after that threshold is exceeded. The major drawback of a simple threshold approach is that it may allow the same object to be categorized in many different ways (e.g., as a fox, a dog, and a wolf), because more than one category may exceed its threshold at the same time.

The best-fit approach is to identify the target object as a member of whatever category has the highest match among a set of mutually exclusive categories.This can be implemented in a “winner-take-all” neural network in which each category unit inhibits every other category unit among some mutually exclusive set. Its main problem lies in the impossibility of deciding that a novel target object is not a member of any known category. This is an issue because there is, by definition, always some category that has the highest similarity to the target object.

The virtues of both decision rules can be combined— with the drawbacks of neither—using a hybrid decision strategy: the best-fit-over-threshold rule. This approach is to set a threshold below which objects will be perceived as novel, but above which the category with the highest matching value is chosen. Such a decision rule can be implemented in a neural network by having internal thresholds for each category unit as well as a winner-take-all network of mutual inhibition among all category units. This combination allows for the possibility of identifying objects as novel without resulting in ambiguity when more than one category exceeds the threshold. It would not be appropriate for deciding among different hierarchically related categories (e.g., collie, dog, and animal), however, because they are not mutually exclusive.

Part-Based Theories

Structural description theories were the most influential approaches to object identification in the late 1970s and 1980s. Various versions were developed by computer scientists and computationally oriented psychologists, including Binford (1971), Biederman (1987), Marr (1982), Marr & Nishihara (1978), and Palmer (1975b). Of the specific theories that have been advanced within this general framework, this research paper describes only one in detail: Biederman’s (1987) recognition by components theory, sometimes called geon theory. It is not radically different from several others, but it is easier to describe and has been developed with more attention to the results of experimental evidence. I therefore present it as representative of this class of models rather than as the correct or even the best one.

Recognition by components (RBC) theory is Biederman’s (1987) attempt to formulate a single, psychologically motivated theory of how people classify objects as members of entry-level categories. It is based on the idea that objects can be specified as spatial arrangements of a small set of volumetric primitives, which Biederman called geons. Object categorization then occurs by matching a geon-based structural description of the target object with corresponding geonbased structural descriptions of object categories. It was later implemented as a neural network (Hummel & Biederman, 1992), but this research paper considers it at the more abstract algorithmic level of Biederman’s (1987) original formulation.

Geons

The first important assumption of RBC theory is that both the stored representations of categories and the representation of a currently attended object are volumetric structural descriptions. Recognition-by-components representations are functional hierarchies whose nodes correspond to a discrete set of three-dimensional volumes (geons) and whose links to other nodes correspond to relations among these geons. Geons are generalized cylinders that have been partitioned into discrete classes by dividing their inherently continuous parameters (see below) into a few discrete ranges that are easy to distinguish from most vantage points. From the relatively small set of 108 distinct geons, a huge number of object representations can be constructed by putting together two or more geons much as an enormous number of words can be constructed by putting together a relatively small number of letters. A few representative geons are illustrated in Figure 7.24 along with some common objects constructed by putting several geons together to form recognizable objects.

Biederman defined the set of 108 geons by making discrete distinctions in the following variable dimensions of generalized cylinders:cross-sectional curvature(straight vs. curved), symmetry (asymmetrical vs. reflectional symmetry alone vs. both reflectional and rotational symmetry), axis curvature (straight vs. curved), cross-sectional size variation (constant vs.expandingandcontractingvs.expandingonly),andaspect ratio of the sweeping axis relative to the largest dimension of the cross-sectional area (approximately equal vs. axis greater vs. cross-section greater). The rationale for these particular distinctions is that, except for aspect ratio, they are qualitative rather than merely quantitative differences that result in qualitatively different retinal projections. The image features that characterize different geons are therefore relatively (but not completely) insensitive to changes in viewpoint.

Because complex objects are conceived in RBC theory as configurations of two or more geons in particular spatial arrangements, they are encoded as structural descriptions that specify both geons and their spatial relations. It is therefore possible to construct different object types by arranging the same geons in different spatial relations, such as the cup and pail in Figure 7.24. RBC theory uses 108 qualitatively different geon relations. Some of them concern how geons are attached (e.g., side-connected and top-connected), whereas others concern their relational properties, such as relative size (e.g., larger than and smaller than). With 108 geon relations and 108 geons, it is logically possible to construct more than a million different two-geon objects. Adding a third geon pushes the number of combinations into the billions. Clearly, geons are capable of generating a rich vocabulary of different complex shapes. Whether it is sufficient to capture the power and versatility of visual categorization is a question to which this discussion returns later.

After the shape of an object has been represented via its component geons and their spatial relations, the problem of object categorization within RBC theory reduces to the process of matching the structural description of an incoming object with the set of structural descriptions for known entrylevel categories. The theory proposes that this process takes place in several stages. In the original formulation, the overall flow of information was depicted in the flowchart of Figure 7.25—(a) An edge extraction process initially produces a line drawing of the edges present in the visual scene; (b) The image-based properties needed to identify geons are extracted from the edge information by detection of nonaccidental properties. The crucial features are the nature of the edges (e.g., curved versus straight), the nature of the vertices (e.g., Y-vertices, K-vertices, L-vertices, etc.), parallelism (parallel vs. nonparallel), and symmetry (symmetric vs. asymmetric). The goal of this process is to provide the feature-based information required to identify the different kinds of geons (see Stage d); (c) At the same time as these features are being extracted, the system attempts to parse objects at regions of deep concavity, as suggested by Hoffman and Richards (1984) and discussed in the section of this research paper entitled “Parsing.” The goal of this parsing process is to divide the object into component geons without having to match them explicitly on the basis of edge and vertex features; (d) The combined results of feature detection (b) and object parsing (c) are used to activate the appropriate geons and spatial relations among them; (e) After the geon description of the input object is constructed, it automatically causes the activation of similar geon descriptions stored in memory. This matching process is accomplished by activation spreading through a network from geon nodes and relation nodes present in the representation of the target object to similar geon nodes and relation nodes in the category representations. This comparison is a fully parallel process, matching the geon description of the input object against all category representations at once and using all geons and relations at once; (f) Finally, object identification occurs when the target object is classified as an instance of the entry-level category that is most strongly activated by the comparison process, provided it exceeds some threshold value.

Although the general flow of information within RBC theory is generally bottom-up, it also allows for top-down processing. If sensory information is weak (e.g., noisy, brief, or otherwise degraded images) top-down effects are likely to occur. There are two points in RBC at which they are most likely to happen: feedback from geons to geon features and feedback from category representations to geons. Contextual effects could also occur through feedback from prior or concurrent object identification to the nodes of related sets of objects, although this level of processing was not actually represented in Biederman’s (1987) model.

View-Specific Theories

In many ways, the starting point for view-specific theories of object identification is the existence of the perspective effects described in the section of this research paper entitled “Perspective Effects.” The fact that recognition and categorization performance is not invariant over different views (e.g., Palmer et al., 1981) raises the possibility that objects might be identified by matching two-dimensional input images directly to some kind of view-specific category representation. It cannot be done with a single, specific view (such as one canonical perspective) because there is simply not enough information in any single view to identify other views. A more realistic possibility is that there might be multiple twodimensional representations from several different viewpoints that can be employed in recognizing objects. These multiple views are likely to be those perspectives from which the object has been seen most often in past experience. As mentioned in this research paper’s section entitled “Orientation Effects,” evidence supporting this possibility has come from a series of experiments that studied the identification of twodimensional figures at different orientations in the frontal plane (Tarr & Pinker, 1989) and of three-dimensional figures at different perspectives (Bülthoff & Edelman, 1992; Edelman & Bülthoff, 1992).

Several theories of object identification encorporate some degree of view specificity. One is Koenderink and Van Doorn’s (1979) aspect graph theory, which is a well-defined elaboration of Minsky’s (1975) frame theory of object perception. An aspect graph is a network of representations containing all topologically distinct two-dimensional views (or aspects) of the same object. Its major problem is that it cannot distinguish among different objects that have the same edge topology. All tetrahedrons are equivalent within aspect graph theory—for example, despite large metric differences that are easily distinguished perceptually. This means that there is more information available to the visual system than is captured by edge topology, a conclusion that led to later theories in which projective geometry plays an important role in matching input views to object representations.

One approach was to match incoming two-dimensional images to internal three-dimensional models by an alignment process (e.g., Huttenlocher & Ullman, 1987; Lowe, 1985; Ullman, 1989). Another was to match incoming twodimensional images directly against stored two-dimensional views, much as template theories advocate (e.g., Poggio & Edelman, 1990; Ullman, 1996; Ullman & Basri, 1991). The latter, exclusively two-dimensional approach has the same problem that plagues template theories of recognition: An indefinitely large number of views would have to be stored. However, modern theorists have discovered computational methods for deriving many two-dimensional views from just a few stored ones, thus suggesting that template-like theories may be more tenable than had originally been supposed.

Ullman and Basri (1991) demonstrated the viability of deriving novel two-dimensional views from a small set of other two-dimensional views, at least under certain restricted conditions, by proving that all possible views of an object can be reconstructed as a linear combination from just three suitably chosen orthographic projections of the same threedimensional object. Figure 7.26 shows some rather striking examples based on this method. Two actual two-dimensional views of a human face (models M1 and M2) have been combined to produce other two-dimensional views of the same face. One is an intermediate view that has been interpolated between the two models (linear combination LC2), and the other two views have been extrapolated beyond them (linear combinations LC1 and LC3). Notice the close resemblance between the interpolated view (LC2) and the actual view from the corresponding viewpoint (novel view N).

This surprising result only holds under very restricted conditions, however, some of which are ecologically unrealistic. Three key assumptions of Ullman and Basri’s (1991) analysis are that (a) all points belonging to the object must be visible in each view, (b) the correct correspondence of all points between each pair of views must be known, and (c) the views must differ only by rigid transformations and by uniform size scaling (dilations). The first assumption requires that none of the points on the object be occluded in any of the three views. This condition holds approximately for wire objects, which are almost fully visible from any viewpoint, but it is violated by almost all other three-dimensional objects due to occlusion. The linear combinations of the faces in Figure 7.26, for example, actually generate the image of a mask of the facial surface itself rather than of the whole head. The difference can be seen by looking carefully at the edges of the face, where the head ends rather abruptly and unnaturally. The linear combination method would not be able to derive a profile view of the same head, because the back of the head is not present in either of the model views (M1 and M2) used to extrapolate other views.

The second assumption requires that the correspondence between points in stored two-dimensional views be known before the views can be combined. Although solving the correspondence problems is a nontrivial computation for complex objects, it can be derived off-line rather than during the process of recognizing an object. The third assumption means that the view combination process will fail to produce an accurate combination if the different two-dimensional views include plastic deformations of the object. If one view is of a person standing and the other of the same person sitting, for instance, their linear combination will not necessarily correspond to any possible view of the person. This restriction thus can cause problems for bodies and faces of animate creatures as well as inanimate objects made of pliant materials (e.g., clothing) or having a jointed structure (e.g., scissors). Computational theorists are currently exploring ways of solving these problems (see Ullman, 1996, for a wide-ranging discussion of such issues), but they are important limitations of the linear combinations approach.

The results obtained by Ullman and Basri (1991) prove that two-dimensional views can be combined to produce new views under the stated conditions, but it does not specify how these views can be used to recognize the object from an input image. Further techniques are required to find a best-fitting match between the input view and the linear combinations of the model views as part of the object recognition process. One approach is to use a small number of features to find the best combination of the model views. Other methods are also possible, but are too technical to be described here. (The interested reader can consult Ullman, 1996, for details.)

Despite the elegance of some of the results that have been obtained by theorists working within the view-specific framework, such theories face serious problems as a general explanation of visual object identification.

1. They do not account well for people’s perceptions of three-dimensional structure in objects. Just from looking at an object, even from a single perspective, people generally know a good deal about its three-dimensional structure, including how to shape their hands to grasp it and what it would feel like if they were to explore it manually. It is not clear how this can occur if their only resource is a structured set of two-dimensional views.
2. Most complex objects have a fairly clear perceived hierarchical structure in terms of parts and subparts. The viewspecific representations previously considered do not contain any explicit representation of such hierarchical structure because they consist of sets of unarticulated points or low-level features, such as edges and vertices. It is not clear, then, how such theories could explain Biederman and Cooper’s (1991) priming experiments on the difference between line and part deletion conditions (see section entitiled “Part Structural Effects”). Ullman (1996) has suggested that parts as well as whole objects may be represented separately in memory. This proposal serves as a reminder that part-based recognition schemes like RBC and view-based schemes are not mutually exclusive, but rather can be combined into various hybrid approaches (e.g., Hummel & Stankiewicz, 1996).
3. Finally, it is not clear how the theory could be extended to handle object identification for entry-level categories. The situations to which view-specific theories have been successfully applied thus far are limited to identical objects that vary only in viewpoint, such as recognizing different views of the same face. The huge variation among different exemplars of chairs, dogs, and houses poses serious problems for view specific theories.

One possible resolution would be that both part-based and view-based processes may be used, but for different kinds of tasks (e.g., Farah, 1992; Tarr & Bülthoff, 1995). Viewspecific representations seem well suited to recognizing the very same object from different perspective views because in that situation, there is no variation in the structure of the object; all the differences between images can be explained by the variation in viewpoint. Recognizing specific objects is difficult for structural description theories, because their representations are seldom specific enough to discriminate between different exemplars. In contrast, structural description theories such as RBC seem well suited to entry level categorization because they have more abstract representations that are better able to encompass shape variations among different exemplars of the same category. This is exactly where view-specific theories have difficulty.

Another possibility is that both view-based and part-based schemes can be combined to achieve the best of both worlds. They are not mutually exclusive, and could even be implemented in parallel (e.g., Hummel & Stankiewicz, 1996). This approach suggests that when the current view matches one stored in view-based form in memory, recognition will be fast and accurate; when it does not, categorization must rely on the slower, more complex process of matching against structural descriptions. Which, if any, of these possible resolutions of the current conflict will turn out to be most productive is not yet clear. The hope is that the controversy will generate interesting predictions that can be tested experimentally, for that is how science progresses.

The foregoing discussion of what is known about perceptual organization and object identification barely scratches the surface of what needs to be known to understand the central mystery of vision: how the responses of millions of independent retinal receptors manage to provide an organism with knowledge of the identities and spatial relations among meaningful objects in its environment. It is indisputable that people achieve such knowledge, that it is evolutionarily important for our survival as individuals and as a species, and that scientists do not yet know how it arises. Despite the enormous amount that has been learned about low-level processing of visual information, the higher-level problems of organization and identification remain largely unsolved. It will take a concerted effort on the part of the entire vision science community—including psychophysicists, cognitive psychologists, physiologists, neuropsychologists, and computer scientists—to reach explanatory solutions. Only then will we begin to understand how the extraordinary feat of perception is accomplished by the visual nervous system.

Bibliography:

1. Anderson, B. L. (1997). A theory of illusory lightness and transparency in monocular and binocular images: The role of contour junctions. Perception, 26(4), 419–453.
2. Asch, S. E., & Witkin, H. A. (1948a). Studies in space orientation: I. Perception of the upright with displaced visual fields. Journal of Experimental Psychology, 38, 325–337.
3. Asch, S. E., &Witkin, H.A. (1948b). Studies in space orientation: II. Perception of the upright with displaced visual fields and with body tilted. Journal of Experimental Psychology, 38, 455–477.
4. Bartram, D. J. (1974). The role of visual and semantic codes in object naming. Cognitive Psychology, 6(3), 325–356.
5. Beck, J. (1966). Effects of orientation and shape similarity on perceptual grouping. Perception and Psychophysics, 1, 300–302.
6. Beck, J. (1972). Similarity grouping and peripheral discriminability under uncertainty. American Journal of Psychology, 85(1), 1–19.
7. Beck, J. (1982). Textural segmentation. In J. Beck (Ed.), Organization and representation in perception (pp. 285–318). Hillsdale, NJ: Lawrence Erlbaum.
8. Biederman, I. (1972). Perceiving real-world scenes. Science, 177 (4043), 77–80.
9. Biederman, I. (1987). Recognition-by-components: A theory of human image understanding. Psychological Review, 94(2), 115– 117.
10. Biederman, I. (1995). Visual identification. In S. M. Kosslyn & D. N. Osherson (Eds.), An invitation to cognitive science: Vol. 2, Visual cognition (pp. 121–165). Cambridge, MA: MIT Press.
11. Biederman, I., & Cooper, E. E. (1991). Priming contour-deleted images: Evidence for intermediate representations in visual object recognition. Cognitive Psychology, 23(3), 393–419.
12. Biederman, I., & Cooper, E. E. (1992). Size invariance in visual object priming. Journal of Experimental Psychology: Human Perception & Performance, 18(1), 121–133.
13. Biederman, I., & Gerhardstein, P. C. (1993). Recognizing depthrotated objects: Evidence and conditions for three-dimensional viewpoint invariance. Journal of Experimental Psychology: Human Perception & Performance, 19(6), 1162–1182.
14. Biederman, I., Glass, A. L., & Stacy, E. W. (1973). Searching for objects in real-world scenes. Journal of Experimental Psychology, 97(1), 22–27.
15. Binford, O. (1971). Visual perception by computer. Paper presented at the IEEE Conference on Systems and Control, Miami, FL.
16. Bucher, N. M., & Palmer, S. E. (1985). Effects of motion on perceived pointing of ambiguous triangles. Perception & Psychophysics, 38(3), 227–236.
17. Buffart, H., & Leeuwenberg, E. L. J. (1981). Structural information theory. In H. G. Geissler, E. L. J. Leeuwenberg, S. Link, & V. Sarris (Eds.), Modern issues in perception. Berlin, Germany: Lawrence Erlbaum.
18. Bülthoff, H. H., & Edelman, S. (1992). Psychophysical support for a two-dimensional interpolation theory of object recognition. Proceedings of the National Academy of Science, USA, 89, 60–64.
19. Canny, J. F. (1986). A computational approach to edge detection. IEEE Transactions on Pattern Analysis and Machine Intelligence, 8, 769–798.
20. Delis, D. C., Robertson, L. C., & Efron, R. (1986). Hemispheric specialization of memory for visual hierarchical stimuli. Neuropsychologia, 24(2), 205–214.
21. DiLorenzo, J. R., & Rock, I. (1982). The rod-and-frame effect as a function of the righting of the frame. Journal of Experimental Psychology: Human Perception & Performance, 8(4), 536– 546.
22. Driver, J., & Baylis, G. C. (1996). Edge-assignment and figure-ground segmentation in short-term visual matching. Cognitive Psychology, 31, 248–306.
23. Ebenholtz, S. M. (1977). Determinants of the rod-and-frame effect: The role of retinal size. Perception & Psychophysics, 22(6), 531–538.
24. Edelman, S., & Bülthoff, H. H. (1992). Orientation dependence in the recognition of familiar and novel views of three-dimensional objects. Vision Research, 32(12), 2385–2400.
25. Ellis, A. W., & Young, A. W. (1988). Human cognitive neuropsychology. Hillsdale, NJ: Erlbaum.
26. Essen, D. C. Van, & DeYoe, E. A. (1995). Concurrent processing in the primate visual cortex. In M. S. Gazzaniga (Ed.), The cognitive neurosciences (pp. 383–400). Cambridge, MA: MIT Press.
27. Farah, M. J. (1990). Visual agnosia: Disorders of object recognition and what they tell us about normal vision. Cambridge, MA: MIT Press.
28. Farah, M. J. (1992). Is an object and object an object?: Cognitive and neuropsychological investigations of domain specificity in visual object recognition. Current Directions in Psychological Science, 1, 164–169.
29. Farah, M. J. (2000). The cognitive neuroscience of vision. Malden, MA: Blackwell Publishers.
30. Gerbino, W. (1994). Achromatic transparency. In A. L. Gilchrist (Ed.), Lightness, brightness, and transparency (pp. 215–255). Hillsdale, NJ: Lawrence Erlbaum.
31. Gibson, E. J. (1969). Principles of perceptual learning and development. New York: Appleton-Century-Crofts.
32. Gibson, J. J. (1979). The ecological approach to visual perception. Boston: Houghton Mifflin.
33. Gregory, R. L. (1972). Cognitive contours. Nature, 238, 51–52.
34. Heydt, R. von der, Peterhans, E., & Baumgartner, G. (1984). Illusory contours and cortical neuron responses. Science, 224 (4654), 1260–1262.
35. Hochberg, , & McAlister, E. (1953). Aquantitative approach to figural “goodness.” Journal of Experimental Psychology, 46, 361–364.
36. Hochberg, J., & Silverstein, A. (1956). Aquantitative index for stimulus similarity: Proximity versus differences in brightness. American Journal of Psychology, 69, 480–482.
37. Hoffman, D. D., & Richards, W. A. (1984). Parts of recognition: Visual cognition [Special issue]. Cognition, 18(1-3), 65–96.
38. Hubel, D. H., & Wiesel, T. N. (1962). Receptive fields, binocular interaction, and functional architecture of the cat’s visual cortex. Journal of Physiology (London), 160, 106–154.
39. Hummel, J. E., & Biederman, I. (1992). Dynamic binding in a neural network for shape recognition. Psychological Review, 99(3), 480–517.
40. Hummel, J. E., & Stankiewicz, B. J. (1996). Categorical relations in shape perception. Spatial Vision, 10(3), 201–236.
41. Huttenlocher, D. P., & Ullman, S. (1987). Object recognition using alignment(MITAIMemoNo.937).Cambridge,MA:MIT.
42. Jolicoeur, P. (1985). The time to name disoriented natural objects. Memory & Cognition, 13(4), 289–303.
43. Jolicoeur, P., Gluck, M. A., & Kosslyn, S. M. (1984). Pictures and names: Making the connection. Cognitive Psychology, 16(2), 243–275.
44. Julesz, B. (1981). Textons, the elements of texture perception, and their interactions. Nature, 290(5802), 91–97.
45. Kanizsa, G. (1955). Margini quasi-percettivi in campi con stimolazione omogenea. Rivista di Psicologia, 49, 7–30.
46. Kanizsa, G. (1979). Organization in vision: Essays on Gestalt perception. New York: Praeger.
47. Kanizsa, G., & Gerbino, W. (1976). Convexity and symmetry in figure-ground organization. In M. Henle (Ed.), Vision and artifact (pp. 25–32). New York: Springer.
48. Kellman, P. J., & Shipley, T. F. (1991). A theory of visual interpolation in object perception. Cognitive Psychology, 23(2), 141–221.
49. Kinchla, R. A., & Wolfe, J. M. (1979). The order of visual processing: “Top-down,” “bottom-up,” or “middle-out.” Perception & Psychophysics, 25(3), 225–231.
50. Koenderink, J. J., & van Doorn, A. J. (1979). The internal representation of solid shape with respect to vision. Biological Cybernetics, 32, 211–216.
51. Koffka, K. (1935). Principles of Gestalt psychology. New York: Harcourt, Brace.
52. Kopferman, H. (1930). Psychologishe Untersuchungen uber die Wirkung Zweidimensionaler korperlicher Gebilde. Psychologische Forschung, 13, 293–364.
53. Kubovy, M., & Gepstein, S. (2000). Gestalt: From phenomena to laws. In K. Boyer & S. Sarkar (Eds.), Perceptual organization for artificial vision systems (pp. 41–72). Dordrecht, the Netherlands: Kluwer Academic.
54. Kubovy, M., & Wagemans, J. (1995). Grouping by proximity and multistability in dot lattices: A quantitative Gestalt theory. Psychological Science, 6(4), 225–234.
55. Leeuwenberg, E. L. J. (1971). A perceptual coding language for visual and auditory patterns. American Journal of Psychology, 84(3), 307–349.
56. Leeuwenberg, E. L. J. (1978). Quantification of certain visual pattern properties: Salience, transparency, and similarity. In E. L. J. Leeuwenberg & H. F. J. M. Buffart (Eds.), Formal theories of visual perception (pp. 277–298). New York: Wiley.
57. Leung, T., & Malik, J. (1998). Contour continuity in region based imagesegmentation.PaperpresentedattheProceedingsofthe 5th European Conference on Computer Vision, Freiburg, Germany.
58. Lissauer, H. (1988). A case of visual agnosia with a contribution to theory. Cognitive Neuropsychology, 5(2), 157–192. (Original work published 1890)
59. Lowe, D. G. (1985). Perceptual organization and visual recognition. Boston, MA: Kluwer Academic.
60. Mach, E. (1959). The analysis of sensations. Chicago: Open Court. (Original work published 1914)
61. Malik, J., & Perona, P. (1990). Preattentive texture discrimination with early vision mechanisms. Journal of the Optical Society of America A, 7(5), 923–932.
62. Marcel, A. J. (1983). Conscious and unconscious perceptions: An approach to the relations between phenomenal experience and perceptual processes. Cognitive Psychology, 15, 238–300.
63. Marr, D. (1982). Vision: A computational investigation into the human representation and processing of visual information. San Francisco: W. H. Freeman.
64. Marr, D., & Hildreth, E. C. (1980). Theory of edge detection. Proceedings of the Royal Society of London: Series B, 207, 187–217.
65. Marr, D., & Nishihara, H. K. (1978). Representation and recognition of the spatial organization of three-dimensional shapes. Proceedings of the Royal Society London, 200, 269–294.
66. Massaro, D. W., & Hary, J. M. (1986). Addressing issues in letter recognition. Psychological Research, 48(3), 123–132.
67. McClelland, J. L., & Rumelhart, D. E. (1981). An interactive activation model of context effects in letter perception: I. An account of basic findings. Psychological Review, 88(5), 375–407.
68. Metelli, F. (1974). The perception of transparency. Scientific American, 230(4), 90–98.
69. Miller, J. (1981). Global precedence in attention and decision. Journal of Experimental Psychology: Human Perception & Performance, 7(6), 1161–1174.
70. Minsky, M. (1975). A framework for representing knowledge. In P. H. Winston (Ed.), The psychology of computer vision (pp. 211–280). New York: McGraw Hill.
71. Nakayama, K., He, Z. J., & Shimojo, S. (1995). Visual surface representation: A critical link between lower-level and higherlevel vision. In S. M. Kosslyn & D. N. Osherson (Eds.), Visual cognition: An invitation to cognitive science (2nd ed., Vol. 2, pp. 1–70). Cambridge, MA: MIT Press.
72. Navon, D. (1976). Irrelevance of figural identity for resolving ambiguities in apparent motion. Journal of Experimental Psychology: Human Perception and Performance, 2, 130–138.
73. Neisser, U. (1967). Cognitive psychology. Englewood Cliffs, NJ: Prentice-Hall.
74. Ober-Thompkins, B. A. (1982). The effects of typicality on picture perception and memory. Unpublished doctoral dissertation, University of California, Berkeley.
75. Palmer, S. E. (1975a). The effects of contextual scenes on the identification of objects. Memory & Cognition, 3(5), 519–526.
76. Palmer, S. E. (1975b). Visual perception and world knowledge: Notes on a model of sensory-cognitive interaction. In D. A. Norman & D. E. Rumelhart (Eds.), Explorations in cognition (pp. 279–307). San Francisco: W. H. Freeman.
77. Palmer, S. E. (1977). Hierarchical structure in perceptual representation. Cognitive Psychology, 9(4), 441–474.
78. Palmer, S. E. (1978). Fundamental aspects of cognitive representation. In E. Rosch & B. Lloyd (Eds.), Cognition and categorization (pp. 261–304). Hillsdale, NJ: Lawrence Erlbaum.
79. Palmer, S. E. (1980). What makes triangles point: Local and global effects in configurations of ambiguous triangles. Cognitive Psychology, 12(3), 285–305.
80. Palmer, S. E. (1985). The role of symmetry in shape perception. Acta Psychologica, 59(1), 67–90.
81. Palmer, S. E. (1989). Reference frames in the perception of shape and orientation. In B. E. Shepp & S. Ballesteros (Eds.), Object perception: Structure and process (pp. 121–163). Hillsdale, NJ: Lawrence Erlbaum.
82. Palmer, S. E. (1992). Common region: A new principle of perceptual grouping. Cognitive Psychology, 24(3), 436–447.
83. Palmer, S. E. (1999). Vision science: Photons to phenomenology. Cambridge, MA: Bradford Books/MIT Press.
84. Palmer, S. E. (2002). Perceptual organization in vision. In H. Pashler (Series Ed.) & S. Yantis (Vol. Ed.), Stevens’Handbook of Experimental Psychology: Vol. 1. Sensation and perception (3rd ed., pp. 177–234). New York: Wiley.
85. Palmer, S. E. (in press-a). Perceptual grouping: It’s later than you think. Current Directions in Psychological Science.
86. Palmer, S. E. (in press-b). Understanding perceptual organization and grouping. In R. Kimchi, M. Behrman, & C. Olson (Eds.), Perceptual organization in vision: Behavioral and neural perspectives. Hillsdale, NJ: Erlbaum.
87. Palmer, S. E., & Bucher, N. M. (1981). Configural effects in perceived pointing of ambiguous triangles. Journal of Experimental Psychology: Human Perception & Performance, 7(1), 88–114.
88. Palmer, S. E., & Bucher, N. M. (1982). Textural effects in perceived pointing of ambiguous triangles. Journal of Experimental Psychology: Human Perception & Performance, 8(5), 693–708.
89. Palmer, S. E., & Levitin, D. (2002). Synchrony: A new principle of perceptual organization. Manuscript in preparation.
90. Palmer, S. E., Neff, J., & Beck, D. (1996). Late influences on perceptual grouping: Amodal completion. Psychonomic Bulletin & Review, 3(1), 75–80.
91. Palmer, S. E., & Nelson, R. (2000). Late influences on perceptual grouping: Illusory contours. Perception & Psychophysics, 62(7), 1321–1331.
92. Palmer, S. E., & Rock, I. (1994a). On the nature and order of organizational processing: A reply to Peterson. Psychonomic Bulletin & Review, 1, 515–519.
93. Palmer, S. E., & Rock, I. (1994b). Rethinking perceptual organization: The role of uniform connectedness. Psychonomic Bulletin & Review, 1(1), 29–55.
94. Palmer, S. E., Rosch, E., & Chase, P. (1981). Cannonical perspective and the perception of objects. In J. Long & A. Baddeley (Eds.), Attention and Performance: Vol. 9. (pp. 135–151). Hillsdale, NJ: Erlbaum.
95. Pentland, A. (1986). Perceptual organization and the representation of natural form. Artificial Intelligence, 28, 293–331.
96. Peterhans, E., & von der Heydt, R. (1991). Subjective contours: Bridging the gap between psychophysics and physiology. Trends in Neurosciences, 14(3), 112–119.
97. Peterson, M.A., & Gibson, B. S. (1991). The initial identification of figure-ground relationships: Contributions from shape recognitionprocesses.BulletinofthePsychonomicSociety,29(3),199– 202.
98. Poggio, T., & Edelman, S. (1990). A neural network that learns to recognize three-dimensional objects. Nature, 343, 263–266.
99. Pomerantz, J. R., Sager, L. C., & Stoever, R. J. (1977). Perception of wholes and of their component parts: Some configural superiority effects. Journal of Experimental Psychology: Human Perception & Performance, 3(3), 422–435.
100. Reed, S. K., & Johnsen, J. A. (1975). Detection of parts in patterns and images. Memory & Cognition, 3(5), 569–575.
101. Reicher, G. M. (1969). Perceptual recognition as a function of meaningfulness of stimulus material. Journal of Experimental Psychology, 81(2), 275–280.
102. Robertson, L. C., Lamb, M. R., & Knight, R. T. (1988). Effects of lesions of the temporal-parietal junction on perceptual and attentional processing in humans. Journal of Neuroscience, 8, 3757–3769.
103. Rock, I. (1973). Orientation and form. New York: Academic Press.
104. Rock, I. (1983). The logic of perception. Cambridge, MA: MIT Press.
105. Rock, I. (1990). The frame of reference. In I. Rock (Ed.), The legacy of Solomon Asch: Essays in cognition and social psychology (pp. 243–268). Hillsdale, NJ: Lawrence Erlbaum.
106. Rock, I., & Brosgole, L. (1964). Grouping based on phenomenal proximity. Journal of Experimental Psychology, 67, 531–538.
107. Rock, I., Nijhawan, R., Palmer, S., & Tudor, L. (1992). Grouping based on phenomenal similarity of achromatic color. Perception, 21(6), 779–789.
108. Rosch, E. (1973). Natural categories. Cognitive Psychology, 4(3), 328–350.
109. Rosch, E. (1975a). Cognitive representations of semantic categories. Journal of Experimental Psychology: General, 104(3), 192–233.
110. Rosch, E. (1975b). The nature of mental codes for color categories. Journal of Experimental Psychology: Human Perception & Performance, 104(1), 303–322.
111. Rosch, E., Mervis, C. B., Gray, W. D., Johnson, D. M., & BoyesBraem, P. (1976). Basic objects in natural categories. Cognitive Psychology, 8(3), 382–439.
112. Rubin, E. (1921). Visuell Wahrgenommene Figuren [Visual perception of figures]. Kobenhaven: Glydenalske boghandel.
113. Rumelhart, D. E., & McClelland, J. L. (1982). An interactive activation model of context effects in letter perception: II. The contextual enhancement effect and some tests and extensions of the model. Psychological Review, 89(1), 60–94.
114. Sacks, O. W. (1985). The man who mistook his wife for a hat and other clinical tales. New York: Summit Books.
115. Schumann, F. (1904). Beitrage zur Analyse der Gesichtswahrnehmungen. Zeitschrift fur Psychologie, 36, 161–185.
116. Shepard, R. N. (1962a). The analysis of proximities: Multidimensional scaling with an unknown distance function: Part I. Psychometrika, 27, 125–140.
117. Shepard, R. N. (1962b). The analysis of proximities: Multidimensional scaling with an unknown distance function: Part II. Psychometrika, 27(3), 219–246.
118. Shi, J., & Malik, J. (1997). Normalized cuts and image segmentation. Paper presented at the Proceedings of the IEEE Conference on Computation: Vision and Pattern Recognition, San Juan, Puerto Rico.
119. Tanaka, J. W., & Taylor, M. (1991). Object categories and expertise: Is the basic level in the eye of the beholder? Cognitive Psychology, 23(3), 457–482.
120. Tarr, M. J., & Bülthoff, H. H. (1995). Is human object recognition better described by geon structural descriptions or by multiple views? Comment on Biederman and Gerhardstein (1993). Journal of Experimental Psychology: Human Perception & Performance, 21(6), 1494–1505.
121. Tarr, M. J., & Pinker, S. (1989). Mental rotation and orientationdependence in shape recognition. Cognitive Psychology, 21(2), 233–282.
122. Teuber, H. L. (1968). Alteration of perception and memory in man: Perception. In L. Weiskrantz (Ed.), Analysis of behavioral change (pp. 274–328). New York: Harper and Row.
123. Tse,P.U.(1999).Volumecompletion.CognitivePsychology,39,37–68.
124. Ullman, S. (1989). Aligning pictorial descriptions: An approach to object recognition. Cognition, 32, 193–254.
125. Ullman, S. (1996). High level vision. Cambridge, MA: MIT Press.
126. Ullman, S., & Basri, R. (1991). Recognition by linear combinations of models. IEEE Transactions on Pattern Analysis and Machine Intelligence, 13(10), 992–1006.
127. Vecera, S. P., Vogel, E. K., & Woodman, G. F. (in press). Lower region: A new cue for figure-ground segregation. Journal of Experimental Psychology: General.
128. Warrington, E. K., & Shallice, T. (1984). Category specific semantic impairments. Brain, 107, 829–854.
129. Warrington, E. K., & Taylor, A. M. (1973). The contribution of the right parietal lobe to object recognition. Cortex, 9(2), 152–164.
130. Warrington, E. K., & Taylor, A. M. (1978). Two categorical stages of object recognition. Perception, 7(6), 695–705.
131. Weisstein, N., & Harris, C. S. (1974). Visual detection of line segments: An object-superiority effect. Science, 186(4165), 752–755.
132. Wenderoth, P. M. (1974). The distinction between the rod-andframe illusion and the rod-and-frame test. Perception, 3(2), 205–212.
133. Wertheimer, M. (1923). Untersuchungen zur Lehre von der Gestalt. Psychology Forschung, 4, 301–350.
134. Wiser, M. (1981). The role of intrinsic axes in shape recognition. Paper presented at the Third Annual Conference of the Cognitive Science Society, Berkeley, CA.