Concepts and Categorization Research Paper

The attraction of research on concepts is that an extremely wide variety of cognitive acts can be understood as categorizations. Identifying the person sitting across from you at the breakfast table involves categorizing something as (for example) your spouse. Diagnosing the cause of someone’s illness involves a disease categorization. Interpreting a painting as a Picasso, an artifact as Mayan, a geometry as non-Euclidean, a fugue as baroque, a conversationalist as charming, a wine as a Bordeaux, and a government as socialist are categorizations at various levels of abstraction. The typically unspoken assumption of research on concepts is that these cognitive acts have something in common. That is, there are principles that explain many or all acts of categorization. This assumption is controversial (see Medin, Lynch, & Solomon, 2000), but is perhaps justified by the potential payoff of discovering common principles governing concepts in their diverse manifestations.

The desirability of a general account of concept learning has led the field to focus its energy on what might be called generic concepts. Experiments typically involve artificial categories that are (it is hoped) unfamiliar to the subject. Formal models of concept learning and use are constructed to be able to handle any kind of concept irrespective of its content. Although there are exceptions to this general trend (Malt, 1994; Ross & Murphy, 1999), much of the mainstream empirical and theoretical work on concept learning is concerned not with explaining how particular concepts are created, but with how concepts in general are represented and processed.

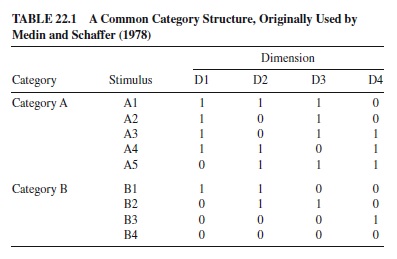
One manifestation of this approach is that the members of a concept are often given an abstract symbolic representation. For example, Table 22.1 shows a typical notation used to describe the stimuli seen by a subject in a psychological experiment or presented to a formal model of concept learning. Nine objects belong to two categories, and each object is defined by its value along four binary dimensions. In this notation, objects from Category A typically have values of 1 on each of the four dimensions, whereas objects from Category B have values of 0. The dimensions are typically unrelated to each other, and assigning values of 0 and 1 to a dimension is arbitrary. For example, for a color dimension, red may be assigned a value of 0 and blue a value 1. The exact category structure of Table 22.1 has been used in at least 30 studies (reviewed by J. D. Smith & Minda, 2000), instantiated by stimuli as diverse as geometric forms (Nosofsky, Kruschke, & McKinley, 1992), cartoons of faces (Medin & Schaffer, 1978), yearbook photographs (Medin, Dewey, & Murphy, 1983), and line drawings of rocketships (Nosofsky,Palmeri,& McKinley, 1994). These authors are not particularly interested in the category structure of Table 22.1 and are certainly not interested in the categorization of rocket ships per se. Instead, they choose their structures and stimuli so as to be (a) unfamiliar (so that learning is required), (b) well controlled (dimensions are approximately equally salient and independent), (c) diagnostic with respect to theories, and (d) potentially generalizable to natural categories that people learn. Work on generic concepts is very valuable if it turns out that there are domain-general principles underlying human concepts that can be discovered. Still, there is no a priori reason to assume that all concepts will follow the same principles, or that we can generalize from generic concepts to naturally occurring concepts.

What Are Concepts?

Concepts, Categories, and Internal Representations

A good starting place is Edward E. Smith’s (1989) characterization that a concept is “a mental representation of a class or individual and deals with what is being represented and how that information is typically used during the categorization” (p. 502). It is common to distinguish between a concept and a category. Aconcept refers to a mentally possessed idea or notion, whereas a category refers to a set of entities that are grouped together. The concept dog is whatever psychological state signifies thoughts of dogs. The category dog consists of all the entities in the real world that are appropriately categorized as dogs. The question of whether concepts determine categories or vice versa is an important foundational controversy. If one assumes the primacy of external categories of entities, then one will tend to view concept learning as the enterprise of inductively creating mental structures that predict these categories. One extreme version of this view is the exemplar model of concept learning (Estes, 1994; Medin & Schaffer, 1978; Nosofsky, 1984; see also Capaldi’s chapter in this volume), in which one’s internal representation for a concept is nothing more than the set of all of the externally supplied examples of the concept to which one has been exposed. If one assumes the primacy of internal mental concepts, then one tends to view external categories as the end product of applying these internal concepts to observed entities. An extreme version of this approach is to argue that the external world does not inherently consist of rocks, dogs, and tables; these are mental concepts that organize an otherwise unstructured external world (Lakoff, 1987).

Equivalence Classes

Another important aspect of concepts is that they are equivalence classes. In the classical notion of an equivalence class, distinguishable stimuli come to be treated as the same thing once they have been placed in the same category (Sidman, 1994). This kind of equivalence is too strong when it comes to human concepts because even when we place two objects into the same category, we do not treat them as the same thing for all purposes. Some researchers have stressed the intrinsic variability of human concepts—variability that makes it unlikely that a concept has the same sense or meaning each time it is used (Barsalou, 1987; Thelen & Smith, 1994). Still, it is impressive the extent to which perceptually dissimilar things can be treated equivalently, given the appropriate conceptualization. To the biologist armed with a strong mammal concept, even whales and dogs may be treated as equivalent in many situations related to biochemistry, child rearing, and thermoregulation. Even sea lions may possess equivalence classes, as Schusterman, Reichmuth, and Kastak (2000) have argued that these animals show free substitution between two entities once they have been associated together.

Equivalence classes are relatively impervious to superficial similarities. Once one has formed a concept that treats all skunks as equivalent for some purposes, irrelevant variations among skunks can be greatly deemphasized. When subjects are told a story in which scientists discover that an animal that looks exactly like a raccoon actually contains the internal organs of a skunk and has skunk parents and skunk children, they often categorize the animal as a skunk (Keil, 1989; Rips, 1989). People may never be able to transcend superficial appearances when categorizing objects (Goldstone, 1994a), nor is it clear that they would want to (Jones & Smith, 1993). Still, one of the most powerful aspects of concepts is their ability to make superficially different things alike (Sloman, 1996). If one has the concept Things to remove from a burning house, even children and jewelry become similar (Barsalou, 1983). The spoken phonemes /d/ /o/ /g/, the French word chien, the written word dog, and a picture of a dog can all trigger one’s concept of dog (Snodgrass, 1984), and although they may trigger slightly different representations, much of the core information will be the same. Concepts are particularly useful when we need to make connections between things that have different apparent forms.

What Do Concepts Do for Us?

Fundamentally, concepts function as filters. We do not have direct access to our external world. We have access to our world only as filtered through our concepts. Concepts are useful when they provide informative or diagnostic ways of structuring this world.An excellent way of understanding the mental world of an individual, group, scientific community,or culture is to find out how they organize their world into concepts (Lakoff, 1987; Medin & Atran, 1999; Wolff, Medin, & Pankratz, 1999).

Components of Thought

Concepts are cognitive elements that combine to generatively produce an infinite variety of thoughts. Just as a finite set of building blocks can be constructed into an endless variety of architectural structures, so can concepts act as building blocks for an endless variety of complex thoughts. Claiming that concepts are cognitive elements does not entail that they are primitive elements in the sense of existing without being learned and without being constructed from other concepts. Some theorists have argued that concepts such as bachelor, kill, and house are primitive in this sense (Fodor, 1975; Fodor, Garrett, Walker, & Parkes, 1980), but a considerable body of evidence suggests that concepts typically are acquired elements that are themselves decomposable into semantic elements (McNamara & Miller, 1989).

Once a concept has been formed, it can enter into compositions with other concepts. Several researchers have studied how novel combinations of concepts are produced and comprehended. For example, how does one interpret the term buffalo paper when one first hears it? Is it paper in the shape of buffalo, paper used to wrap buffaloes presented as gifts, an essay on the subject of buffalo, coarse paper, or something like fly paper but used to catch bison? Interpretations of word combinations are often created by finding a relation that connects the two concepts. In Murphy’s (1988) concept specialization model, one interprets noun-noun combinations by finding a variable that the second noun has that can be filled by the first noun. By this account, a robin snake might be interpreted as a snake that eats robins once robin is used to the fill the eats slot in the snake concept. Wisniewski (1997, 1998; Wisniewski & Love, 1998) has argued that properties from one concept are often transferred to another concept, and that this is more likely to occur if the concepts are similar, with parts that can be easily aligned. By this account, a robin snake may be interpreted as a snake with a red belly, once the attribute red breast from the robin is transferred to the snake.

In addition to promoting creative thought, the combinatorial power of concepts is required for cognitive systematicity (Fodor & Pylyshyn, 1988). The notion of systematicity is that a system’s ability to entertain complex thoughts is intrinsically connected to its ability to entertain the components of those thoughts. In the field of conceptual combination, this has appeared as the issue of whether the meaning of a combination of concepts can be deduced on the basis of the meanings of its constituents. On the one hand, there are some salient violations of this type of systematicity. When adjective and noun concepts are combined, there are sometimes emergent interactions that cannot be predicted by the “main effects” of the concepts themselves. For example, the concept gray hair is more similar to white hair than to black hair, but gray cloud is more similar to black cloud than to white cloud (Medin & Shoben, 1988). Wooden spoons are judged to be fairly large (for spoons), even though this property is not generally possessed by wooden objects or spoons in general (Medin & Shoben, 1988). On the other hand, there have been notable successes in predicting how well an object fits a conjunctive description based on how well it fits the individual descriptions that comprise the conjunction (Hampton, 1987, 1997; Storms, De Boeck, Hampton, & Van Mechelen, 1999). A reasonable reconciliation of these results is that when concepts are combined the concepts’meanings systematically determine the meaning of the conjunction, but emergent interactions and real-world plausibility also shape the conjunction’s meaning.

Inductive Predictions

Concepts allow us to generalize our experiences with some objects to other objects from the same category. Experience with one slobbering dog may lead one to suspect that an unfamiliar dog may have the same proclivity. These inductive generalizations may be wrong and can lead to unfair stereotypes if inadequately supported by data, but if an organism is to survive in a world that has some systematicity, it must “go beyond the information given” (Bruner, 1973) and generalize what it has learned. The concepts we use most often are useful because they allow many properties to be predicted inductively. To see why this is the case, we must digress slightly and consider different types of concepts. Categories can be arranged roughly in order of their grounding by similarity: natural kinds (dog and oak tree), man-made artifacts (hammer, airplane, and chair), ad hoc categories (things to take out of a burning house, and things that could be stood on to reach a lightbulb), and abstract schemas or metaphors (e.g., events in which a kind action is repaid with cruelty, metaphorical prisons, and problems that are solved by breaking a large force into parts that converge on a target). For the latter categories, members need not have very much in common at all. An unrewarding job and a relationship that cannot be ended may both be metaphorical prisons, but the situations may share little other than this.

Unlike ad hoc and metaphor-based categories, most natural kinds and many artifacts are characterized by members that share many features. In a series of studies, Rosch (Rosch, 1975; Rosch & Mervis, 1975; see also the chapters in this volume by Palmer and by Treiman, Clifton, Meyer, & Wurm) has shown that the members of natural kind and artifact “basic-level” categories such as chair, trout, bus, apple, saw, and guitar are characterized by high within-category overall similarity. Subjects listed features for basic-level categories, as well as for broader superordinate (e.g., furniture) and narrower subordinate (e.g., kitchen chair) categories. An index of within-category similarity was obtained by tallying the number of features listed by subjects that were common to items in the same category. Items within a basic-level category tend to have several features in common, far more than items within a superordinate category and almost as many as items that share a subordinate categorization. Rosch (Rosch & Mervis, 1975; Rosch, Mervis, Gray, Johnson, & Boyes-Braem, 1976) argues that categories are defined by family resemblance; category members need not all share a definitional feature, but they tend to have several features in common. Furthermore, she argues that people’s basic-level categories preserve the intrinsic correlational structure of the world. All feature combinations are not equally likely. For example, in the animal kingdom, flying is correlated with laying eggs and possessing a beak. There are “clumps” of features that tend to occur together. Some categories (e.g., ad hoc categories) do not conform to these clumps, but many of our most natural-seeming categories do.

These natural categories also permit many inductive inferences. If we know something belongs to the category dog, then we know that it probably has four legs and two eyes, eats dog food, is someone’s pet, pants, barks, is bigger than a breadbox, and so on. Generally, natural-kind objects, particularly those at Rosch’s basic level, permit many inferences. Basic-level categories allow many inductions because their members share similarities across many dimensions or features. Ad hoc categories and highly metaphorical categories permit fewer inductive inferences, but in certain situations the inferences they allow are so important that the categories are created on a “by-need” basis. One interesting possibility is that all concepts are created to fulfill an inductive need, and that standard taxonomic categories such as bird and hammer simply become automatically triggered because they have been used often, whereas ad hoc categories are created only when specifically needed (Barsalou, 1982, 1991). In any case, evaluating the inductive potential of a concept goes a long way toward understanding why we have the concepts that we do. The single concept peaches, llamas, telephone answering machines, or Ringo Starr is an unlikely concept because belonging in this concept predicts very little. Several researchers have been formally developing the notion that the concepts we possess are those that maximize inductive potential (Anderson, 1991; Heit, 2000; Oaksford & Chater, 1998).

Communication

Communication between people is enormously facilitated if the people can count upon sharing a set of common concepts. By uttering a simple sentence such as “Ed is a football player,” one can transmit a wealth of information to a colleague, dealing with the probabilities of Ed’s being strong, having violent tendencies, being a college physics or physical education major, and having a history of steroid use. Markman and Makin (1998) have argued that a major force in shaping our concepts is the need to communicate efficiently. They find that a person’s concepts become more consistent and systematic over time in order to establish reference unambiguously for another individual with whom they need to communicate (see also Garrod & Doherty, 1994).

Cognitive Economy

We can discriminate far more stimuli than those for which we have concepts. For example, estimates suggest that we can perceptually discriminate at least 10,000 colors from each other, but we have far fewer color concepts than this. Dramatic savings in storage requirements can be achieved by encoding concepts rather than entire raw (unprocessed) inputs. A classic study by Posner and Keele (1967) found that subjects code letters such as A by a raw, physical code, but that this code rapidly (within 2 s) gives way to a more abstract conceptual code that A and a share. Huttenlocher, Hedges, and Vevea (2000) develop a formal model in which judgments about a stimulus are based on both its category membership and its individuating information. As predicted by the model, when subjects are asked to reproduce a stimulus, their reproductions reflect a compromise between the stimulus itself and the category to which it belongs. When a delay is introduced between seeing the stimulus and reproducing it, the contribution of category-level information relative to individual-level information increases (Crawford, Huttenlocher, & Engebretson, 2000). Together with studies showing that, over time, people tend to preserve the gist of a category rather than the exact members that constitute it (e.g., Posner & Keele, 1970), these results suggest that through the preservation of category-level information rather than individual-level information, efficient long-term representations can be maintained.

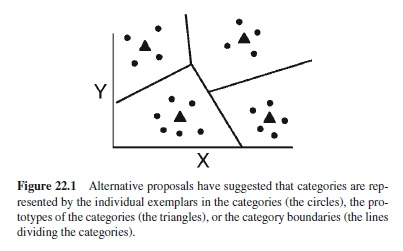
From an information-theory perspective, storing a category in memory rather than a complete description of an individual is efficient because fewer bits of information are required to specify the category. For example, Figure 22.1 depicts a set of objects (shown by circles) described along two dimensions. Rather than preserving the complete description of each of the 19 objects, one can create a reasonably faithful representation of the distribution of objects by storing only the positions of the four triangles in Figure 22.1. This kind of information reduction is particularly significant because computational algorithms exist that can automatically form these categories when supplied with the objects (Kohonen, 1995). For example, the competitive learning algorithm (Rumelhart & Zipser, 1985) begins with random positions for the triangles, and when an object is presented, the triangle that is closest to the object moves its position even closer to the object. The other triangles move less quickly, or do not move at all, leaving them free to specialize for other classes of objects. In addition to showing a way in which efficient category representations can be created, this algorithm has been put forth as a model of how a person creates categories even when there is no teacher, parent, or label that tells the person what, or how many, categories there are.

The above argument suggests that concepts can be used to conserve memory. An equally important economizing advantage of concepts is to reduce the need for learning (Bruner, Goodnow, & Austin, 1956). An unfamiliar object that has not been placed in a category attracts attention because the observer must figure out how to think of it. Conversely, if an object can be identified as belonging to a preestablished category, then less cognitive processing is typically necessary. One can simply treat the object as another instance of something that is known, updating one’s knowledge slightly, if at all. The difference between events that require altering one’s concepts and those that do not was described by Piaget (1952) in terms of accommodation (adjusting concepts on the basis of a new event) and assimilation (applying already known concepts to an event). This distinction has also been incorporated into computational models of concept learning that determine whether an input can be assimilated into a previously learned concept. If it cannot, then reconceptualization is triggered (Grossberg, 1982). When a category instance is consistent with a simple category description, then an individual is less likely to store a detailed description of it than if it is an exceptional item (Palmeri & Nosofsky, 1995), consistent with the notion that people simply use an existing category description when it suffices.

How Are Concepts Represented?

Much of the research on concepts and categorization revolves around the issue of how concepts are mentally represented. As with all discussion of representations, the standard caveat must be issued—mental representations cannot be determined or used without processes that operate on these representations (Anderson, 1978). Rather than discussing the representation of a concept such as cat, we should discuss a representation-process pair that allows for the use of this concept. Empirical results interpreted as favoring a particular representation format should almost always be interpreted as supporting a particular representation given particular processes that use the representation. As a simple example, when trying to decide whether a shadowy figure briefly glimpsed was a cat or fox, one needs to know more than how one’s cat and fox concepts are represented. One needs to know how the information in these representations is integrated to make the final categorization. Does one wait for the amount of confirmatory evidence for one of the animals to rise above a certain threshold (Busemeyer & Townsend, 1993)? Does one compare the evidence for the two animals and choose the more likely (Luce, 1959)? Is the information in the candidate animal concepts accessed simultaneously or successively? Probabilistically or deterministically? These are all questions about the processes that use conceptual representations. One reaction to the insufficiency of representations alone to account for concept use has been to dispense with all reference to independent representations, and instead to frame theories in terms of dynamic processes alone (Thelen & Smith, 1994; van Gelder, 1998). However, some researchers feel that this is a case of throwing out the baby with the bath water, and insist that representations must still be posited to account for enduring, organized, and rulegoverned thought (Markman & Dietrich, 2000).

Rules

There is considerable intuitive appeal to the notion that concepts are represented by something like dictionary entries. By a rule-based account of concept representation, to possess the concept cat is to know the dictionary entry for it. A person’s cat concept may differ from Webster’s Dictionary entry: “a carnivorous mammal (Felis catus) long domesticated and kept as a pet and for catching rats and mice.” Still, this account claims that a concept is represented by some rule that allows one to determine whether an entity belongs within the category (see also the chapter by Leighton & Sternberg in this volume).

The most influential rule-based approach to concepts may be Bruner, Goodnow, and Austin’s (1956) hypothesis-testing approach. Their theorizing was, in part, a reaction against behaviorist approaches (Hull, 1920) in which concept learning involved the relatively passive acquisition of an association between a stimulus (an object to be categorized) and a response (such as a verbal response, key press, or labeling). Instead, Bruner et al. argued that concept learning typically involves active hypothesis formation and testing. In a typical experiment, their subjects were shown flash cards that had different shapes, colors, quantities, and borders. The subjects’ task was to discover the rule for categorizing the flash cards by selecting cards to be tested and by receiving feedback from the experimenter indicating whether the selected card fit the categorizing rule. The researchers documented different strategies for selecting cards, and a considerable body of subsequent work (e.g., Bourne, 1970) showed large differences in how easily acquired are different categorization rules. For example, a conjunctive rule such as white and square is more easily learned than a conditional rule such as if white, then square, which is in turn more easily learned than a biconditional rule such as white if and only if square.

A parallel development to these laboratory studies of artificial categories was Katz and Fodor’s (1963) semantic marker theory of compositional semantics within linguistics. In this theory, a word’s semantic representation consists of a list of atomic semantic markers such as + Male, +Adult, + Physical, and – Married for the word bachelor. These markers serve as the components of a rule that specifies when a word is appropriately used. Each of the semantic markers for a word is assumed to be necessary for something to belong to the word category, and the markers are assumed to be jointly sufficient to make the categorization.

The assumptions of these rule-based models have been vigorously challenged for several decades now (see the chapter by Treiman et al. in this volume). Douglas Medin and Edward E. Smith (Medin & Smith, 1984; E. E. Smith & Medin, 1981) dubbed this rule-based approach “the classical view,” and characterized it as holding that all instances of a concept share common properties that are necessary and sufficient conditions for defining the concept. At least three criticisms have been levied against this classical view.

First, it has proven to be very difficult to specify the defining rules for most concepts. Wittgenstein (1953) raised this point with his famous example of the concept game. He argued that none of the candidate definitions of this concept, such as activity engaged in for fun, activity with certain rules, or competitive activity with winners and losers, is adequate to identify Frisbee, professional baseball, and roulette as games, while simultaneously excluding wars, debates, television viewing, and leisure walking from the game category. Even a seemingly well-defined concept such as bachelor seems to involve more than its simple definition of unmarried male. The counterexample of a 5-year-old child (who does not really seem to be a bachelor) may be solved by adding an adult precondition to the unmarried male condition, but an indefinite number of other preconditions is required to exclude a man in a long-term but unmarried relationship, the Pope, and a 80-year-old widower with four children (Lakoff, 1987). Wittgenstein argued that instead of equating knowing a concept with knowing a definition, it is better to think of the members of a category as being related by family resemblance. A set of objects related by family resemblance need not have any particular feature in common, but will have several features that are characteristic or typical of the set.

Second, the category membership for some objects is unclear. People may disagree on whether a starfish is a fish, a camel is a vehicle, a hammer is a weapon, or a stroke is a disease. By itself, this is not too problematic for a rule-based approach. People may use rules to categorize objects, but different people may have different rules. However, it turns out that people not only disagree with each other about whether a bat is mammal—they also disagree with themselves! McCloskey and Glucksberg (1978) showed that subjects give surprisingly inconsistent category membership judgments when asked the same questions at different times. Either there is variability in how to apply a categorization rule to an object, people spontaneously change their categorization rules, or (as many researchers believe) people simply do not represent objects in terms of clear-cut rules.

Third, even when a person shows consistency in placing objects in a category, he or she might not treat all the objects as equally good members of that category. By a rule-based account, one might argue that all objects that match a category rule would be considered equally good members of the category (but see Bourne, 1982). However, when subjects are asked to rate the typicality of animals such as a robin and an eagle for the category bird, or a chair and a hammock for the category furniture, they reliably give different typicality ratings for different objects. Rosch and Mervis (1975) were able to predict typicality ratings with respectable accuracy by asking subjects to list properties of category members, and measuring how many properties possessed by a category member were shared by other category members. The magnitude of this so-called “family resemblance measure” is positively correlated with typicality ratings.

Despite these strong challenges to the classical view, the rule-based approach is by no means moribund. In fact, in part due to the perceived lack of constraints in neural network models that learn concepts by gradually building up associations, the rule-based approach experienced a rekindling of interest in the 1990s after its low point in the 1970s and 1980s (Marcus, 1998). Nosofsky and Palmeri (1998; Nosofsky et al., 1994; Palmeri & Nosofsky, 1995) have proposed a quantitative model of human concept learning that learns to classify objects by forming simple logical rules and remembering occasional exceptions to those rules. This work is reminiscent of earlier computational models of human learning that created rules such as if white and square, then Category 1 from experience with specific examples (Anderson, Kline, & Beasley, 1979; Medin, Wattenmaker, & Michalski, 1987). The models have a bias to create simple rules, and are able to predict entire distributions of subjects’ categorization responses rather than simply average responses.

In defending a role for rule-based reasoning in human cognition, E. E. Smith, Langston, and Nisbett (1992) proposed eight criteria for determining whether people use abstract rules in reasoning. These criteria include the following: “Performance on rule-governed items is as accurate with abstract as with concrete material”; “performance on rulegoverned items is as accurate with unfamiliar as with familiar material”; and “performance on a rule-governed item or problem deteriorates as a function of the number of rules that are required for solving the problem.” Based on the full set of criteria, they argue that rule-based reasoning does occur, and that it may be a mode of reasoning distinct from associationbased or similarity-based reasoning. Similarly, Pinker (1991) argued for distinct rule-based and association-based modes for determining linguistic categories. Neurophysiological support for this distinction comes from studies showing that rule-based and similarity-based categorization involve anatomically separate brain regions (Ashby, Alfonso-Reese, Turken, & Waldron, 1998; Ashby & Waldron, 2000; E. E. Smith, Patalano, & Jonides, 1998).

In developing a similar distinction between similaritybased and rule-based categorization, Sloman (1996) introduced the notion that the two systems can simultaneously generate different solutions to a reasoning problem. For example, Rips (1989; see also Rips & Collins, 1993) asked subjects to imagine a 3 in. (7.62 cm) round object, and then asked whether the object is more similar to a quarter or a pizza, and whether the object is more likely to be a pizza or a quarter. There is a tendency for the object to be judged as more similar to a quarter, but as more likely to be a pizza. The rule that quarters must not be greater than 1 in. plays a larger role in the categorization decision than in the similarity judgment, causing the two judgments to dissociate. By Sloman’s analysis, the tension we feel about the categorization of the 3-in. object stems from the two different systems’ indicating incompatible categorizations. Sloman argues that the rulebased system can suppress the similarity-based system but cannot completely suspend it. When Rips’s experiment is repeated with a richer description of the object to be categorized, categorization again tracks similarity, and people tend to choose the quarter for both the categorization and similarity choices (E. E. Smith & Sloman, 1994).

Prototypes

Just as the active hypothesis-testing approach of the classical view was a reaction against the passive stimulus–response association approach, so the prototype model was developed as a reaction against what was seen as the overly analytic, rule-based classical view. Central to Eleanor Rosch’s development of prototype theory is the notion that concepts are organized around family resemblances rather than features that are individually necessary and jointly sufficient for categorization (Mervis & Rosch, 1981; Rosch, 1975; Rosch & Mervis, 1975; see also the chapters in this volume by Capaldi, by Palmer, and by Treiman et al.). The prototype for a category consists of the most common attribute values associated with the members of the category, and can be empirically derived by the previously described method of asking subjects to generate a list of attributes for several members of a category. Once prototypes for a set of concepts have been determined, categorizations can be predicted by determining how similar an object is to each of the prototypes. The likelihood of placing an object into a category increases as it becomes more similar to the category’s prototype and less similar to other category prototypes (Rosch & Mervis, 1975).

This prototype model can naturally deal with the three problems that confronted the classical view. It is no problem if defining rules for a category are difficult or impossible to devise. If concepts are organized around prototypes, then only characteristic (not necessary or sufficient) features are expected. Unclear category boundaries are expected if objects are presented that are approximately equally similar to prototypes from more than one concept. Objects that clearly belong to a category may still vary in their typicality because they may be more similar to the category’s prototype than to any other category’s prototype, but they still may differ in how similar they are to the prototype. Prototype models do not require “fuzzy” boundaries around concepts (Hampton, 1993), but prototype similarities are based on commonalities across many attributes and are consequently graded, and lead naturally to categories with graded membership.

A considerable body of data has been amassed that suggests that prototypes have cognitively important functions. The similarity of an item to its category prototype (in terms of featural overlap) predicts the results from several converging tasks. Somewhat obviously, it is correlated with the average rating the item receives when subjects are asked to rate how good an example the item is of its category (Rosch, 1975). It is correlated with subjects’ speed in verifying statements of the form “An [item] is a [category name]” (E. E. Smith, Shoben, & Rips, 1974). It is correlated with subjects’ frequency and speed of listing the item when asked to supply members of a category (Mervis & Rosch, 1981). It is correlated with the probability of inductively extending a property from the item to other members of the category (Rips, 1975). Taken in total, these results indicate that different members of the same category differ in how typical they are of the category, and that these differences have a strong cognitive impact. Many natural categories seem to be organized not around definitive boundaries, but by graded typicality to the category’s prototype.

The prototype model described previously generates category prototypes by finding the most common attribute values shared among category members. An alternative conception views a prototype as the central tendency of continuously varying attributes. If the four observed members of a lizard category had tail lengths of 3, 3, 3, and 7 in., the former prototype model would store a value of 3 (the modal value) as the prototype’s tail length, whereas the central tendency model would store a value of 4 (the average value). The central tendency approach has proven useful in modeling categories composed of artificial stimuli that vary on continuous dimensions. For example, Posner and Keele’s (1968) classic dot-pattern stimuli consisted of nine dots positioned randomly or in familiar configurations on a 30 × 30 invisible grid. Each prototype was a particular configuration of dots, but during categorization training, subjects never saw the prototypes themselves. Instead, they saw distortions of the prototypes obtained by shifting each dot randomly by a small amount. Categorization training involved subjects’seeing dot patterns, guessing their category assignment, and receiving feedback indicating whether their guesses were correct or not. During a transfer stage, Posner and Keele found that subjects were better able to categorize the never-before-seen category prototypes than they were to categorize new distortions of those prototypes. In addition, subjects’ accuracy in categorizing distortions of category prototypes was strongly correlated with the proximity of those distortions to the never-before-seen prototypes. The authors interpreted these results as suggesting that prototypes are extracted from distortions, and used as a basis for determining categorizations (see also Homa, Sterling, & Trepel, 1981).

Exemplars

Exemplar models deny that prototypes are explicitly extracted from individual cases, stored in memory, and used to categorize new objects. Instead, in exemplar models, a conceptual representation consists of only those actual, individual cases that one has observed. The prototype representation for the category bird consists of the most typical bird, or an assemblage of the most common attribute values across all birds, or the central tendency of all attribute values for observed birds. By contrast, an exemplar model represents the category bird by representing all of the instances (exemplars) that belong to this category (Brooks, 1978; Estes, 1986, 1994; Hintzman, 1986; Kruschke, 1992; Lamberts, 1998, 2000; Logan, 1988; Medin & Schaffer, 1978; Nosofsky, 1984, 1986; see also the chapter by Capaldi in this volume).

Although the prime motivation for these models has been to provide good fits to results from human experiments, computer scientists have pursued similar models with the aim to exploit the power of storing individual exposures to stimuli in a relatively raw, unabstracted form. Exemplar, instancebased (Aha, 1992), view-based (Tarr & Gauthier, 1998), case-based (Schank, 1982), nearest neighbor (Ripley, 1996), configural cue (Gluck & Bower, 1990), and vector quantization (Kohonen, 1995) models all share the fundamental insight that novel patterns can be identified, recognized, or categorized by giving the novel patterns the same response that was learned for similar, previously presented patterns. By creating representations for presented patterns, not only is it possible to respond to repetitions of these patterns; it is also possible to give responses to novel patterns that are likely to be correct by sampling responses to old patterns, weighted by their similarity to the novel patterns. Consistent with these models, psychological evidence suggests that people show good transfer to new stimuli in perceptual tasks only to the extent that the new stimuli superficially resemble previously learned stimuli (Kolers & Roediger, 1984; Palmeri, 1997).

The frequent inability of human generalization to transcend superficial similarities might be considered evidence for either human stupidity or laziness. To the contrary, if a strong theory about which stimulus features promote valid inductions is lacking, the strategy of least commitment is to preserve the entire stimulus in its full richness of detail (Brooks, 1978). That is, by storing entire instances and basing generalizations on all of the features of these instances, one can be confident that one’s generalizations are not systematically biased. It has been shown that in many situations, categorizing new instances by their similarity to old instances maximizes the likelihood of categorizing the new instances correctly (Ashby & Maddox, 1993; McKinley & Nosofsky, 1995; Ripley, 1996). Furthermore, if information later becomes available that specifies which properties are useful for generalizing appropriately, then preserving entire instances will allow these properties to be recovered. Such properties might be lost and unrecoverable if people were less “lazy” in their generalizations from instances.

Given these considerations, it is understandable that people often use all of the attributes of an object even when a task demands the use of specific attributes. Doctors’ diagnoses of skin disorders are facilitated when they are similar to previously presented cases, even when the similarity is based on attributes that are known to be irrelevant for the diagnosis (Brooks, Norman, & Allen, 1991). Even when subjects know a simple, clear-cut rule for a perceptual classification, performance is better on frequently presented items than rare items (Allen & Brooks, 1991). Consistent with exemplar models, responses to stimuli are frequently based on their overall similarity to previously exposed stimuli.

The exemplar approach assumes that a category is represented by the category exemplars that have been encountered, and that categorization decisions are based on the similarity of the object to be categorized to all of the exemplars of each relevant category. As such, as an item becomes more similar to the exemplars of Category A (or less similar to the exemplars of other categories), then the probability that it will be placed in Category A increases. Categorization judgments may shift if an item is approximately equally close to two sets of exemplars, because probabilistic decision rules are typically used. Items will vary in their typicality to a category as long as they vary in their similarity to the aggregate set of exemplars.

The exemplar approach to categorization raises a number of questions. First, once one has decided that concepts are to be represented in terms of sets of exemplars, the obvious question remains: How are the exemplars to be represented? Some exemplar models use a featural or attribute-value representation for each of the exemplars (Hintzman, 1986; Medin & Schaffer, 1978).Another popular approach is to represent exemplars as points in a multidimensional psychological space. These points are obtained by measuring the subjective similarity of every object in a set to every other object. Once an N × N matrix of similarities between N objects has been determined by similarity ratings, perceptual confusions, spontaneous sortings, or other methods, a statistical technique called multidimensional scaling (MDS) finds coordinates for the objects in a D-dimensional space that allow the N × N matrix of similarities to be reconstructed with as little error as possible (Nosofsky, 1992). Given that D is typically smaller than N, a reduced representation is created in which each object is represented in terms of its values on D dimensions. Distances between objects in these quantitatively derived spaces can be used as the input to exemplar models to determine item-toexemplar similarities. These MDS representations are useful for generating quantitative exemplar models that can be fit to human categorizations and similarity judgments, but these still beg the question of how a stand-alone computer program or a person would generate these MDS representations. Presumably, there is some human process that computes object representations and can derive object-to-object similarities from them, but this process is not currently modeled by exemplar models (for steps in this direction, see Edelman, 1999).

A second question for exemplar models is, If exemplar models do not explicitly extract prototypes, how can they account for results that concepts are organized around prototypes? A useful place to begin is by considering Posner and Keele’s (1968) result that the never-before-seen prototype is categorized better than new distortions based on the prototype. Exemplar models have been able to model this result because a categorization of an object is based on its summed similarity to all previously stored exemplars (Medin & Schaffer, 1978; Nosofsky, 1986). The prototype of a category will, on average, be more similar to the training distortions than are new distortions because the prototype was used to generate all of the training distortions. Without our positing the explicit extraction of the prototype, the cumulative effect of many exemplars in an exemplar model can create an emergent, epiphenomenal advantage for the prototype.

Given the exemplar model’s account of prototype categorization, one might ask whether predictions from exemplar and prototype models differ. In fact, they typically do, in large part because categorizations in exemplar models are not simply based on summed similarity to category exemplars, but to similarities weighted by the proximity of an exemplar to the item to be categorized. In particular, exemplar models have mechanisms to bias categorization decisions so that they are more influenced by exemplars that are similar to items to be categorized. In Medin and Schaffer’s (1978) context model, this is achieved through computing the similarity between objects by multiplying rather than adding their similarities on each of their features. In Hintzman’s (1986) Minerva model, this is achieved by raising object-to-object similarities to a power of 3 before summing them together. In Nosofsky’s Generalized Context Model (1986), this is achieved by basing object-to-object similarities on an exponential function of the objects’ distance in an MDS space. With these quantitative biases for close exemplars, the exemplar model does a better job of predicting categorization accuracy for Posner and Keele’s experiment than the prototype model because it can also predict that familiar distortions will be categorized more accurately than novel distortions that are equally far removed from the prototype (Shin & Nosofsky, 1992).

A third question for exemplar models is, In what way are concept representations economical if every experienced exemplar is stored? It is certainly implausible with large realworld categories to suppose that every instance ever experienced is stored in a separate trace. However, more realistic exemplar models may either store only part of the information associated with an exemplar (Lassaline & Logan, 1993), or only some of the exemplars (Aha, 1992; Palmeri & Nosofsky, 1995). One particularly interesting way of conserving space that has received empirical support (Barsalou, Huttenlocher, & Lamberts, 1998) is to combine separate events that all constitute a single individual into a single representation. Rather than passively registering every event as distinct, people seem naturally to consolidate events that refer to the same individual. If an observer fails to register the difference between a new exemplar and a previously encountered exemplar (e.g., two similar-looking chihuahuas), then he or she may combine the two, resulting in an exemplar representation that is a blend of two instances.

Category Boundaries

Another notion is that a concept representation describes the boundary around a category. The prototype model would represent the four categories of Figure 22.1 in terms of the triangles. The exemplar model represents the categories by the circles. The category boundary model would represent the categories by the four dividing lines between the categories. This view has been most closely associated with the work of Ashby and his colleagues (Ashby, 1992; Ashby et al., 1998; Ashby & Gott, 1988; Ashby & Maddox, 1993; Ashby & Townsend, 1986; Maddox & Ashby, 1993). It is particularly interesting to contrast the prototype and category boundary approaches, because their representational assumptions are almost perfectly complementary. The prototype model represents a category in terms of its most typical member—the object in the center of the distribution of items included in the category. The category boundary model represents categories by their periphery, not their center.

An interesting phenomenon to consider with respect to whether centers or peripheries of concepts are representationally privileged is categorical perception. According to this phenomenon, people are better able to distinguish between physically different stimuli when the stimuli come from different categories than when they come from the same category (see Harnad, 1987, for several reviews of research; see also the chapters in this volume by Fowler and by Treiman et al.). The effect has been best documented for speech phoneme categories. For example, Liberman, Harris, Hoffman, and Griffith (1957) generated a continuum of equally spaced consonant-vowel syllables going from /be/ to /de/. Observers listened to three sounds—A followed by B followed by X—and indicated whether X was identical to A or B. Subjects performed the task more accurately when syllables A and B belonged to different phonemic categories than when they were variants of the same phoneme, even when physical differences were equated.

Categorical perception effects have been observed for visual categories (Calder, Young, Perrett, Etcoff, & Rowland, 1996) and for arbitrarily created laboratory categories (Goldstone, 1994b). Categorical perception could emerge from either prototype or boundary representations. An item to be categorized might be compared to the prototypes of two candidate categories. Increased sensitivity at the category boundary would exist because people represent items in terms of the prototypes to which they are closest. Items that fall on different sides of a boundary would have very different representations because they would be closest to different prototypes (Liberman et al., 1957). Alternatively, the boundary itself might be represented as a reference point, and as pairs of items move closer to the boundary, it becomes easier to discriminate between them because of their proximity to this reference point (Pastore, 1987).

Computational models have been developed that operate on both principles. Following the prototype approach, Harnad, Hanson, and Lubin (1995) describe a neural network in which the representation of an item is “pulled” toward the prototype of the category to which it belongs. Following the boundaries approach, Goldstone, Steyvers, Spencer-Smith, and Kersten (2000) describe a neural network that learns to strongly represent critical boundaries between categories by shifting perceptual detectors to these regions. Empirically, the results are mixed. Consistent with prototypes’ being represented, some researchers have found particularly good discriminability close to a familiar prototype (Acker, Pastore, & Hall, 1995; McFadden & Callaway, 1999). Consistent with boundaries’ being represented, other researchers have found that the sensitivity peaks associated with categorical perception heavily depend on the saliency of perceptual cues at the boundary (Kuhl & Miller, 1975). Rather than being arbitrarily fixed, a category boundary is most likely to occur at a location where a distinctive perceptual cue, such as the difference between an aspirated and unaspirated speech sound, is present. A possible reconciliation is that information about either the center or periphery of a category can be represented, and that boundary information is more likely to be represented when two highly similar categories must be frequently discriminated and there is a salient reference point for the boundary.

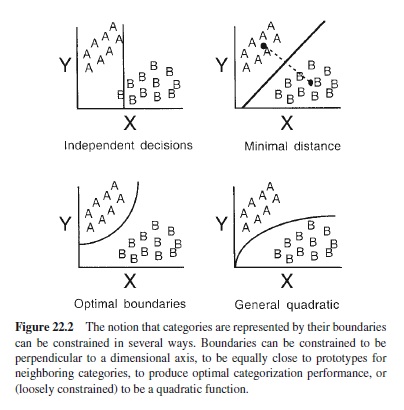
Different versions of the category boundary approach, illustrated in Figure 22.2, have been based on different ways of partitioning categories (Ashby & Maddox, 1998). With independent decision boundaries, category boundaries must be perpendicular to a dimensional axis, forming rules such as Category A items are larger than 3 cm, irrespective of their color. This kind of boundary is appropriate when the dimensions that make up a stimulus are difficult to integrate (Ashby & Gott, 1988). With minimal distance boundaries, a Category A response is given if and only if an object is closer to the Category Aprototype than the Category B prototype. The decision boundary is formed by finding the line that connects the two categories’ prototypes, and creating a boundary that bisects and is orthogonal to this line. The optimal boundary is the boundary that maximizes the likelihood of correctly categorizing an object. If the two categories have the same patterns of variability on their dimensions, and people use information about variance to form their boundaries, then the optimal boundary will be a straight line. If the categories differ in variability, then the optimal boundary will be described by a quadratic equation (Ashby & Maddox, 1993, 1998). A general quadratic boundary is any boundary that can be described by a quadratic equation.

One difficulty with representing a concept by a boundary is that the location of the boundary between two categories depends on several contextual factors. For example, Repp and Liberman (1987) argue that categories of speech sounds are influenced by order effects, adaptation, and the surrounding speech context. The same sound that is halfway between [pa] and [ba] will be categorized as /pa/ if preceded by several repetitions of a prototypical [ba] sound, but categorized as /ba/ if preceded by several [pa] sounds. For a category boundary representation to accommodate this, two category boundaries would need to hypothesized—a relatively permanent category boundary between /ba/ and /pa/, and a second boundary that shifts depending upon the immediate context. The relatively permanent boundary is needed because the contextualized boundary must be based on some earlier information. In many cases, it is more parsimonious to hypothesize representations for the category members themselves, and to view category boundaries as side effects of the competition between neighboring categories. Context effects are then explained simply by changes to the strengths associated with different categories. By this account, there may be no reified boundary around one’s cat concept that causally affects categorizations. When asked about a particular object we can decide whether it is a cat, but this is done by comparing the evidence in favor of the object’s being a cat to its being something else.

Theories

The representation approaches considered thus far all work irrespectively of the actual meaning of the concepts. This is both an advantage and a liability. It is an advantage because it allows the approaches to be universally applicable to any kind of material. They share with inductive statistical techniques the property that they can operate on any data set once the data set is formally described in terms of numbers, features, or coordinates. However, the generality of these approaches is also a liability if the meaning or semantic content of a concept influences how it is represented. While few would argue that statistical t-tests are appropriate only for certain domains of inquiry (e.g., testing political differences, but not disease differences), many researchers have argued that the use of purely data-driven, inductive methods for concept learning are strongly limited and modulated by the background knowledge one has about a concept (Carey, 1985; Gelman & Markman, 1986; Keil, 1989; Medin, 1989; Murphy & Medin, 1985).

People’s categorizations seem to depend on the theories they have about the world (for reviews, see Komatsu, 1992; Medin, 1989). Theories involve organized systems of knowledge. In making an argument for the use of theories in categorization, Murphy and Medin (1985) provide the example of a man jumping into a swimming pool fully clothed. This man may be categorized as drunk because we have a theory of behavior and inebriation that explains the man’s action. Murphy and Medin argue that the categorization of the man’s behavior does not depend on matching the man’s features to those of the category drunk. It is highly unlikely that the category drunk would have such a specific feature as jumps into pools fully clothed. It is not the similarity between the instance and the category that determines the instance’s classification; it is the fact that our category provides a theory that explains the behavior.

Other researchers have empirically supported the dissociation between theory-derived categorization and similarity. In one experiment, Carey (1985) observes that children choose a toy monkey over a worm as being more similar to a human, but that when they are told that humans have spleens, are more likely to infer that the worm has a spleen than that the toy monkey does. Thus, the categorization of objects into spleen and no-spleen groups does not appear to depend on the same knowledge that guides similarity judgments. Carey argues that even young children have a theory of living things. Part of this theory is the notion that living things have self-propelled motion and rich internal organizations. Children as young as 3 years of age make inferences about an animal’s properties on the basis of its category label even when the label opposes superficial visual similarity (Gelman & Markman, 1986; see also the chapter by Treiman et al. in this volume).

Using different empirical techniques, Keil (1989) has come to a similar conclusion. In one experiment, children are told a story in which scientists discover that an animal that looks exactly like a raccoon actually contains the internal organs of a skunk and has skunk parents and skunk children. With increasing age, children increasingly claim that the animal is a skunk. That is, there is a developmental trend for children to categorize on the basis of theories of heredity and biology rather than on visual appearance. In a similar experiment, Rips (1989) shows an explicit dissociation between categorization judgments and similarity judgments in adults. An animal that is transformed (by toxic waste) from a bird into something that looks like an insect is judged by subjects to be more similar to an insect, but is also judged to be a bird still. Again, the category judgment seems to depend on biological, genetic, and historical knowledge, whereas the similarity judgments seems to depend more on gross visual appearance.

Researchers have explored the importance of background knowledge in shaping our concepts by manipulating this knowledge experimentally. Concepts are more easily learned when a learner has appropriate background knowledge, indicating that more than “brute” statistical regularities underlie our concepts (Pazzani, 1991). Similarly, when the features of a category can be connected through prior knowledge, category learning is facilitated (Murphy & Allopenna, 1994; Spalding & Murphy, 1999). Even a single instance of a category can allow one to form a coherent category if background knowledge constrains the interpretation of this instance (Ahn, Brewer, & Mooney, 1992). Concepts are disproportionately represented in terms of concept features that are tightly connected to other features (Sloman, Love, & Ahn, 1998).

Forming categories on the basis of data-driven, statistical evidence and forming them based upon knowledge-rich theories of the world seem like strategies fundamentally at odds with each other. Indeed, this is probably the most basic difference between theories of concepts. However, these approaches need not be mutually exclusive. Even the most outspoken proponents of theory-based concepts do not claim that similarity-based or statistical approaches are not also needed (Murphy & Medin, 1985). Moreover, some researchers have suggested integrating the two approaches. Heit (1994, 1997) describes a similarity-based, exemplar model of categorization that incorporates background knowledge by storing category members as they are observed (as with all exemplar models), but also storing never-seen instances that are consistent with the background knowledge. Choi, McDaniel, and Busemeyer (1993) described a neural network model of concept learning that does not begin with random or neutral connections between features and concepts (as is typical), but begins with theory-consistent connections that are relatively strong. Both approaches allow domaingeneral category learners to also have biases toward learning categories consistent with background knowledge.

Summary to Representation Approaches

One cynical conclusion to reach from the preceding alternative approaches is that a researcher begins with a theory, then tends to find evidence consistent with the theory (a result that is meta-analytically consistent with a theory-based approach!). Although this state of affairs is typical throughout the field of psychology, it is particularly rife in conceptlearning research because researchers have a significant amount of flexibility in choosing what concepts they will experimentally use. Evidence for rule-based categories tends to be found with categories that are created from simple rules (Bruner, Goodnow, & Austin, 1956). Evidence for prototypes tends to be found for categories made up of members that are distortions around single prototypes (Posner & Keele, 1968). Evidence for exemplar models is particular strong when categories include exceptional instances that must be individually memorized (Nosofsky & Palmeri, 1998; Nosofsky et al., 1994). Evidence for theories is found when categories are created that subjects already know something about (Murphy & Kaplan, 2000). The researcher’s choice of representation seems to determine the experiment that is conducted, rather than the experiment’s influencing the choice of representation.

There may be a grain of truth to this cynical conclusion, but our conclusions are instead that people use multiple representational strategies, and can flexibly deploy these strategies based upon the categories to be learned. From this perspective, representational strategies should be evaluated according to their trade-offs and for their fit to the real-world categories and empirical results. For example, exemplar representations are costly in terms of storage demands, but are sensitive to interactions between features and adaptable to new categorization demands. There is a growing consensus that at least two kinds of representational strategy are both present but separated—rule-based and similarity-based processes (Erickson & Kruschke, 1998; Pinker, 1991; Sloman, 1996). Other researchers have argued for separate processes for storing exemplars and extracting prototypes (Knowlton & Squire, 1993; J. D. Smith & Minda, 2000). Even if one holds out hope for a unified model of concept learning, it is important to recognize these different representational strategies as special cases that must be achievable by the unified model given the appropriate inputs.

Connecting Concepts

Although knowledge representation approaches have often treated conceptual systems as independent networks that gain their meaning by their internal connections (Lenat & Feigenbaum, 1991), it is important to remember that concepts are connected to both perception and language. Concepts’ connections to perception serve to ground them (Harnad, 1990), and their connections to language allow them to transcend direct experience and to be transmitted easily.

Connecting Concepts to Perception

Concept formation is often studied as though it were a modular process (in the sense of Fodor, 1983). For example, participants in category-learning experiments are often presented with verbal feature lists representing the objects to be categorized. The use of this method suggests an implicit assumption that the perceptual analysis of an object into features is complete before one begins to categorize that object. This may be a useful simplifying assumption, allowing a researcher to test theories of how features are combined to form concepts. There is mounting evidence, however, that the relationship between the formation of concepts and the identification of features is bidirectional (Goldstone & Barsalou, 1998). In particular, not only does the identification of features influence the categorization of an object, but also the categorization of an object influences the interpretation of features (Bassok, 1996).

In this section of the chapter, we will review the evidence for a bidirectional relationship between concept formation and perception. Evidence for an influence of perception on concept formation comes from the classic study of Heider (1972). She presented a paired-associate learning task involving colors and words to the Dani, a population in New Guinea that has only two color terms. Participants were given a different verbal label for each of 16 color chips. They were then presented with each of the chips and asked for the appropriate label. The correct label was given as feedback when participants made incorrect responses, allowing participants to learn the new color terms over the course of training.

The key manipulation in this experiment was that 8 of the color chips represented English focal colors, whereas 8 represented colors that were not prototypical examples of one of the basic English color categories. Both English speakers and Dani were found to be more accurate at providing the correct label for the focal color chips than for the nonfocal color chips, where focal colors are those that have a consistent and strong label in English. Heider’s (1972) explanation for this finding was that the English division of the color spectrum into color categories is not arbitrary, but rather reflects the sensitivities of the human perceptual system. Because the Dani share these same perceptual sensitivities with English speakers, they were better at distinguishing focal colors than nonfocal colors, allowing them to learn color categories for focal colors more easily.

Further research provides evidence for a role of perceptual information not only in the formation but also in the use of concepts. This evidence comes from research relating to Barsalou’s (1999) theory of perceptual symbol systems. According to this theory, sensorimotor areas of the brain that are activated during the initial perception of an event are reactivated at a later time by association areas, serving as a representation of one’s prior perceptual experience. Rather than preserving a verbatim record of what was experienced, however, association areas only reactivate certain aspects of one’s perceptual experience, namely those that received attention. Because these reactivated aspects of experience may be common to a number of different events, they may be thought of as symbols, representing an entire class of events. Because they are formed around perceptual experience, however, they are perceptual symbols, unlike the amodal symbols typically employed in symbolic theories of cognition.

Barsalou’s (1999) theory suggests a powerful influence of perception on the formation and use of concepts. Evidence consistent with this proposal comes from property verification tasks. Solomon and Barsalou (1999) presented participants with a number of concept words, each followed by a property word, and asked participants whether each property was a part of the corresponding concept. Half of the participants were instructed to use visual imagery to perform the task, whereas half were given no specific instructions. Despite this difference in instructions, participants in both conditions were found to perform in a qualitatively similar manner. In particular, reaction times of participants in both conditions were predicted most strongly by the perceptual characteristics of properties. For example, participants were quicker to verify small properties of objects than to verify large properties. Findings such as this suggest that detailed perceptual information is represented in concepts and that this information is used when reasoning about those concepts.

There is also evidence for an influence of concepts on perception. Classic evidence for such an influence comes from research on the previously described phenomenon of categorical perception. Listeners are much better at perceiving contrasts that are representative of different phoneme categories (Liberman, Cooper, Shankweiler, & Studdert-Kennedy, 1967). For example, listeners can hear the difference in voice onset time between the words bill and pill, even when this difference is no greater than the difference between two /b/ sounds that cannot be distinguished. One may simply argue that categorical perception provides further evidence of an influence of perception on concepts. In particular, the phonemes of language may have evolved to reflect the sensitivities of the human perceptual system. Evidence consistent with this viewpoint comes from the fact that chinchillas are sensitive to many of the same sound contrasts as are humans, even though chinchillas obviously have no language (Kuhl & Miller, 1975; see also the chapter by Treiman et al. in this volume). There is evidence, however, that the phonemes to which a listener is sensitive can be modified by experience. In particular, although newborn babies appear to be sensitive to all of the sound contrasts present in all of the world’s languages, a 1-year-old can hear only those sound contrasts present in his or her linguistic environment (Werker & Tees, 1984). Thus, children growing up in Japan lose the ability to distinguish between the /l/ and /r/ phonemes, whereas children growing up in the United States retain this ability (Miyawaki, 1975). The categories of language thus influence one’s perceptual sensitivities, providing evidence for an influence of concepts on perception.

Although categorical perception was originally demonstrated in the context of auditory perception, similar phenomena have since been discovered in vision. For example, Goldstone (1994b) trained participants to make a category discrimination in terms of either the size or the brightness of an object. He then presented those participants with a samedifferent task, in which two briefly presented objects were either the same or varied in terms of size or brightness. Participants who had earlier categorized objects on the basis of a particular dimension were found to perform better at telling objects apart in terms of that dimension than were control participants who had been given no prior categorization training. Moreover, this sensitization of categorically relevant dimensions was most evident at those values of the dimension that straddled the boundary between categories.

These findings thus provide evidence that the concepts that one has learned influence one’s perceptual sensitivities, in the visual as well as in the auditory modality. Other research has shown that prolonged experience with a domain such as dogs (Tanaka & Taylor, 1991) or faces (Levin & Beale, 2000; O’Toole, Peterson, & Deffenbacher, 1995) leads to development of a perceptual system that is tuned to these domains. Goldstone et al. (2000) review other evidence for conceptual influences on visual perception. Concept learning appears to be effective both in combining stimulus properties to create perceptual chunks that are diagnostic for categorization (Goldstone, 2000), and in splitting apart and isolating perceptual dimensions if they are differentially diagnostic for categorization (Goldstone & Steyvers, 2001).

The evidence reviewed here suggests that there is a strong interrelationship between concepts and perception, with perceptual information influencing the concepts that one forms and conceptual information influencing how one perceives the world. Most theories of concept formation fail to account for this interrelationship. They instead take the perceptual attributes of a stimulus as a given and try to account for how these attributes are used to categorize that stimulus.

One area of research that provides an exception to this rule is research on object recognition. As pointed out by Schyns (1998), object recognition can be thought of as an example of object categorization, with the goal of the process being to identify what kind of object one is observing. Unlike theories of categorization, theories of object recognition place strong emphasis on the role of perceptual information in identifying an object.

Interestingly, some of the theories that have been proposed to account for object recognition have characteristics in common with theories of categorization. For example, structural description theories of object recognition (e.g., Biederman, 1987; Hummel & Biederman, 1992; Marr & Nishihara, 1978; see also the chapter by Palmer in this volume) are similar to prototype theories of categorization in that a newly encountered exemplar is compared to a summary representation of a category in order to determine whether the exemplar is a member of that category. In contrast, multiple-views theories of object recognition (e.g., Edelman, 1998; Tarr & Bülthoff, 1995; see also Palmer’s chapter in this volume) are similar to exemplar-based theories of categorization in that a newly encountered exemplar is compared to a number of previously encountered exemplars stored in memory. The categorization of an exemplar is determined either by the exemplar in memory that most closely matches it or by a computation of the similarities of the new exemplar to each of a number of stored exemplars.

The similarities in the models proposed to account for categorization and object recognition suggest that there is considerable opportunity for cross-talk between these two domains. For example, theories of categorization could potentially be adapted to provide a more complete account for object recognition. In particular, they may be able to provide an account of not only the recognition of established object categories, but also the learning of new ones, a problem not typically addressed by theories of object recognition. Furthermore, theories of object recognition could be adapted to provide a better account of the role of perceptual information in concept formation and use. The rapid recent developments in object recognition research, including the development of detailed computational, neurally based models (e.g., Perrett, Oram, & Ashbridge, 1998), suggest that a careful consideration of the role of perceptual information in categorization can be a profitable research strategy.

Connecting Concepts to Language

Concepts also take part in a bidirectional relationship with language. In particular, one’s repertoire of concepts may influence the types of word meanings that one learns, whereas the language that one speaks may influence the types of concepts that one forms.

The first of these two proposals is the less controversial. It is widely believed that children come into the process of vocabulary learning with a large set of unlabeled concepts. These early concepts may reflect the correlational structure in the environment of the young child, as suggested by Rosch et al. (1976). For example, a child may form a concept of dog around the correlated properties of four legs, tail, wagging, slobbering, and so forth. The subsequent learning of a word’s meaning should be relatively easy to the extent that one can map that word onto one of these existing concepts.

Different kinds of words may vary in the extent to which they map directly onto existing concepts, and thus some types of words may be learned more easily than others. For example, Gentner (1981, 1982; Gentner & Boroditsky, 2001) has proposed that nouns can be mapped straightforwardly onto existing object concepts, and that nouns are thus learned relatively early by children. The relation of verbs to prelinguistic event categories, on the other hand, may be less straightforward. The nature of children’s prelinguistic event categories is not very well understood, but the available evidence suggests that they are structured quite differently from verb meanings. In particular, research by Kersten and Billman (1997) demonstrated that when adults learned event categories in the absence of category labels, they formed those categories around a rich set of correlated properties, including the characteristics of the objects in the event, the motions of those objects, and the outcome of the event. Research by Cohen and Oakes (1993) has similarly demonstrated that 10-month-old infants learned unlabeled event categories involving correlations among different aspects of an event, in this case between the agent in an event and the outcome of a causal interaction involving that agent. These unlabeled event categories learned by children and adults differ markedly from verb meanings. Verb meanings tend to have limited correlational structure, instead picking out only a small number of properties of an event (Huttenlocher & Lui, 1979; Talmy, 1985). For example, the verb collide involves two objects moving into contact with one another, irrespective of the objects involved or the outcome of this collision.

Verbs thus cannot be mapped directly onto existing event categories. Instead, language-learning experience is necessary to determine which aspects of an event are relevant and which aspects are irrelevant to verb meanings. Perhaps as a result, children learning a variety of different languages have been found to learn verbs later than nouns (Au, Dapretto, & Song, 1994; Gentner, 1982; Gentner & Boroditsky, 2000; but see Gopnik & Choi, 1995, and Tardif, 1996, for possible exceptions). More generally, word meanings should be easy to learn to the extent that they can be mapped onto existing concepts.

There is greater controversy regarding the extent to which language may influence one’s concepts. Some influences of language on concepts are fairly straightforward, however. For example, whether a concept is learned in the presence or absence of language (e.g., a category label) may influence the way in which that concept is learned. When categories are learned in the presence of a category label, a common finding is one of competition among correlated cues for predictive strength (Gluck & Bower, 1988; Shanks, 1991). In particular, more salient cues may overshadow less salient cues, causing the concept learner to fail to notice the predictiveness of the less salient cue (Gluck & Bower, 1988; Kruschke, 1992; Shanks, 1991).

When categories are learned in the absence of a category label, on the other hand, there is facilitation rather than competition among correlated predictors of category membership (Billman, 1989; Billman & Knutson, 1996; Cabrera & Billman, 1996; Kersten & Billman, 1997). The learning of unlabeled categories has been measured in terms of the learning of correlations among attributes of a stimulus. For example, one’s knowledge of the correlation between a wagging tail and a slobbering mouth can be used as a measure of one’s knowledge of the category dog. Billman and Knutson (1996) used this method to examine the learning of unlabeled categories of novel animals. They found that participants were more likely to learn the predictiveness of an attribute when other correlated predictors were also present.

The key difference between these two concept-learning situations may be that in the learning of labeled categories, one piece of information, namely the category label, is singled out as being important to predict. Thus, when participants can adequately predict the category label on the basis of a single attribute, they need not look to additional attributes. On the other hand, when no one piece of information is singled out, as in the case of unlabeled categories, participants who have learned one predictive relation cannot be sure that they have learned all that they need to learn. As a result, they may continue looking for additional predictive relations. In doing so, they may preferentially attend to those attributes that have already been discovered to be useful, resulting in facilitated learning of further relations involving those attributes (Billman & Heit, 1988).

There is thus evidence that the presence of language influences the way in which a concept is learned. A more controversial suggestion is that the language that one speaks may influence the types of concepts that one is capable of learning. This suggestion, termed the linguistic relativity hypothesis, was first made by Whorf (1956) on the basis of apparent dramatic differences between English and Native American languages in their expressions of ideas such as time, motion, and color. For example, Whorf proposed that the Hopi have no concept of time because the Hopi language provides no mechanism for talking about time. Many of Whorf’s linguistic analyses have since been debunked (see Pinker, 1994, for a review), but his theory remains a source of controversy.

Early experimental evidence suggested that concepts were relatively impervious to linguistic influences. In particular, Heider’s (1972) finding that the Dani learned new color concepts in a similar fashion to English speakers, despite the fact that the Dani had only two color words, suggested that concepts were determined by perception rather than by language. More recently, however, Roberson, Davies, and Davidoff (2000) attempted to replicate Heider’s findings with another group of people with a limited color vocabulary, the Berinmo of New Guinea. In contrast to Heider’s findings, Roberson et al. found that the Berinmo performed no better at learning a new color concept for a focal color than for a nonfocal color. Moreover, the Berinmo performed no better at learning a category discrimination between green and blue (a distinction not made in their language) than they did at learning a discrimination between two shades of green. This result contrasted with the results of English-speaking participants, who performed better at the green-blue discrimination. It also contrasted with superior Berinmo performance on a discrimination that was present in their language. These results suggest that the English division of the color spectrum may be more a function of the English language and less a function of human color physiology than was originally believed.

Regardless of one’s interpretation of the Heider (1972) and Roberson et al. (2000) results, there are straightforward reasons to expect at least some influence of language on one’s concepts. Homa and Cultice (1984) have demonstrated that people are better at learning concepts when category labels are provided as feedback. Thus, at the very least, one may expect that a concept will be more likely to be learned when it is labeled in a language than when it is unlabeled. Although this may seem obvious, further predictions are possible when this finding is combined with the evidence for influences of concepts on perception reviewed earlier. In particular, on the basis of the results of Goldstone (1994b), one may predict that when a language makes reference to a particular dimension, thus causing people to learn concepts around that dimension, people’s perceptual sensitivities to that dimension will be increased. This, in turn, will make people who learn this language more likely to notice further contrasts along this dimension. Thus, language may influence people’s concepts indirectly through one’s perceptual abilities.

This proposal is consistent with L. B. Smith’s (1999) account of the apparent shape bias in children’s word learning. Smith proposed that children learn over the course of early language acquisition that the shapes of objects are important in distinguishing different nouns. As a result, they attend more strongly to shape in subsequent word learning, resulting in an acceleration in subsequent shape-word learning. Although this proposal is consistent with an influence of language on concepts, languages do not seem to differ very much in the extent to which they refer to the shapes of objects (Gentner, 1982; Gentner & Boroditsky, 2001), and thus one would not expect speakers of different languages to differ in the extent to which they are sensitive to shape.

Languages do differ in other respects, however, most notably in their use of verbs (Gentner & Boroditsky, 2001; Kersten, 1998). In English, the most frequently used class of verbs refers to the manner of motion of an object (e.g., running, skipping, sauntering), or the way in which an object moves around (Talmy, 1985). In other languages (e.g., Spanish), however, the most frequently used class of verbs refers to the path of an object (e.g., entering, exiting), or its direction with respect to some external reference point. In these languages, manner of motion is relegated to an adverbial, if it is mentioned at all. If language influences one’s perceptual sensitivities, it is possible that English speakers and Spanish speakers may differ in the extent to which they are sensitive to motion attributes such as the path and manner of motion of an object.

Suggestive evidence in this regard comes from a study by Naigles and Terrazas (1998). They found that English speakers were more likely to generalize a novel verb to an event involving the same manner of motion and a different path than to an event involving the same path and a different manner of motion, whereas Spanish speakers showed the opposite tendency. One possible account of this result is that English speakers attended more strongly to manner of motion than did Spanish speakers, causing English speakers to be more likely to map the new verb onto manner of motion. If this were the case, it would have important implications for learning a second language. In particular, one may have difficulty attending to contrasts in a second language that are not explicitly marked in one’s native language.

Thus, although the evidence for influences of language on one’s concepts is mixed, there are reasons to believe that some such influence may take place, if only at the level of attention to different attributes of a stimulus. Proponents of the universalist viewpoint (e.g., Pinker, 1994) may argue that this level of influence is a far cry from the strongest interpretation of Whorf’s hypothesis that language determines the concepts that one is capable of learning. A more fruitful approach, however, may be to stop arguing about whether a given result supports Whorf’s theory and start testing more specific theories regarding the relationship between language and concepts.

The Future of Concepts and Categorization

The field of concept learning and representation is noteworthy for its large number of directions and perspectives. Although the lack of closure may frustrate some outside observers, it is also a source of strength and resilience. With an eye toward the future, we describe some of the most important avenues for future progress in the field.

First, as the previous section suggests, we believe that much of the progress of research on concepts will be to connect concepts to other concepts (Goldstone, 1996; Landauer & Dumais, 1997), to the perceptual world, and to language. One of the risks of viewing concepts as represented by rules, prototypes, sets of exemplars, or category boundaries is that one can easily imagine that one concept is independent of others. For example, one can list the exemplars that are included in the concept bird, or describe its central tendency, without making recourse to any other concepts. However, it is likely that all of our concepts are embedded in a network in which each concept’s meaning depends on other concepts as well as on perceptual processes and linguistic labels. The proper level of analysis may not be individual concepts, as many researchers have assumed, but systems of concepts. The connections between concepts and perception on the one hand and between concepts and language on the other hand reveal an important dual nature of concepts. Concepts are used both to recognize objects and to ground word meanings. Working out the details of this dual nature will go a long way toward understanding how human thinking can be both concrete and symbolic.

A second direction is the development of more sophisticated formal models of concept learning. Progress in neural networks, mathematical models, statistical models, and rational analyses can be gauged by several measures: goodness of fit to human data, breadth of empirical phenomena accommodated, model constraint and parsimony, and autonomy from human intervention. The current crop of models is fairly impressive in terms of fitting specific data sets, but there is much room for improvement in terms of their ability to accommodate rich sets of concepts and to process real-world stimuli without relying on human judgments or hand coding.

A final important direction will be to apply psychological research on concepts (see also the chapter by Nickerson & Pew in this volume). Perhaps the most important and relevant application is in the area of educational reform. Psychologists have amassed a large amount of empirical research on various factors that impact the ease of learning and transferring conceptual knowledge. The literature contains excellent suggestions on how to manipulate category labels, presentation order, learning strategies, stimulus format, and category variability in order to optimize the efficiency and likelihood of concept attainment. Putting these suggestions to use in classrooms, computer-based tutorials, and multimedia instructional systems could have a substantial positive impact on pedagogy. This research can also be used to develop autonomous computer diagnosis systems, user models, information visualization systems, and databases that are organized in a manner consistent with human conceptual systems. Given the importance of concepts for intelligent thought, it is not unreasonable to suppose that concept learning research will be equally important for improving thought processes.

Bibliography:

1. Acker, B. E., Pastore, R. E., & Hall, M. D. (1995). Within-category discrimination of musical chords: Perceptual magnet or anchor? Perception & Psychophysics, 57, 863–874.
2. Aha, D. W. (1992). Tolerating noisy, irrelevant and novel attributes in instance-based learning algorithms. International Journal of Man Machine Studies, 36, 267–287.
3. Ahn, W.-K., Brewer, W. F., & Mooney, R. J. (1992). Schema acquisition from a single example. Journal of Experimental Psychology: Learning, Memory, and Cognition, 18, 391–412.
4. Allen, S. W., & Brooks, L. R. (1991). Specializing the operation of an explicit rule. Journal of Experimental Psychology: General, 120, 3–19.
5. Anderson, J. R. (1978). Arguments concerning representations for mental imagery. Psychological Review, 85, 249–277.
6. Anderson, J. R. (1991). The adaptive nature of human categorization. Psychological Review, 98, 409–429.
7. Anderson, J. R., Kline, P. J., & Beasley, C. M., Jr. (1979). A general learning theory and its application to schema abstraction. Psychology of Learning and Motivation, 13, 277–318.
8. Ashby, F. G. (1992). Multidimensional models of perception and cognition. Hillsdale, NJ: Erlbaum.
9. Ashby, F. G., Alfonso-Reese, L. A., Turken, A. U., & Waldron, E. M. (1998). A neuropsychological theory of multiple systems in category learning. Psychological Review, 10, 442–481.
10. Ashby, F. G., & Gott, R. (1988). Decision rules in perception and categorization of multidimensional stimuli. Journal of Experimental Psychology: Learning, Memory, and Cognition, 14, 33–53.
11. Ashby, F. G., & Maddox, W. T. (1993). Relations among prototype, exemplar, and decision bound models of categorization. Journal of Mathematical Psychology, 38, 423–466.
12. Ashby, F. G., & Maddox, W. T. (1998). Stimulus categorization. In M. H. Birnbaum (Ed.), Measurement, judgment, and decision making: Handbook of perception and cognition (pp. 251–301). San Diego, CA: Academic Press.
13. Ashby, F. G., & Townsend, J. T. (1986). Varieties of perceptual independence. Psychological Review, 93, 154–179.
14. Ashby, F. G., & Waldron, E. M. (2000). The neuropsychological bases of category learning. Current Directions in Psychological Science, 9, 10–14.
15. Au, T. K., Dapretto, M., & Song, Y. K. (1994). Input vs. constraints: EarlywordacquisitioninKoreanandEnglish.JournalofMemory and Language, 33, 567–582.
16. Barsalou, L.W. (1982). Context-independent and context-dependent information in concepts. Memory & Cognition, 10, 82–93.
17. Barsalou, L. W. (1983). Ad hoc categories. Memory & Cognition, 11, 211–227.
18. Barsalou, L. W. (1987). The instability of graded structure: Implications for the nature of concepts. In U. Neisser (Ed.),Concepts and conceptual development (pp. 101–140). New York: Cambridge University Press.
19. Barsalou, L. W. (1991). Deriving categories to achieve goals. In G. H. Bower (Ed.), The psychology of learning and motivation: Advances in research and theory (Vol. 27, pp. 1–64). New York: Academic Press.
20. Barsalou, L. W. (1999). Perceptual symbol systems. Behavioral and Brain Sciences, 22, 577–660.
21. Barsalou, L. W., Huttenlocher, J., & Lamberts, K. (1998). Basing categorization on individuals and events. Cognitive Psychology, 36, 203–272.
22. Bassok, M. (1996). Using content to interpret structure: Effects on analogical transfer. Current Directions in Psychological Science, 5, 54–58.

23. Biederman, I. (1987). Recognition-by-components: A theory of human image understanding. Psychological Review, 94, 115– 147.
24. Billman, D. (1989). Systems of correlations in rule and category learning: Use of structured input in learning syntactic categories. Language and Cognitive Processes, 4, 127–155.
25. Billman, D., & Heit, E. (1988). Observational learning from internal feedback: A simulation of an adaptive learning method. Cognitive Science, 12, 587–625.
26. Billman, D., & Knutson, J. F. (1996). Unsupervised concept learning and value systematicity: A complex whole aids learning the parts. Journal of Experimental Psychology: Learning, Memory, and Cognition, 22, 458–475.
27. Bourne, L. E., Jr. (1970). Knowing and using concepts. Psychological Review, 77, 546–556.
28. Bourne, L. E., Jr. (1982). Typicality effect in logically defined categories. Memory & Cognition, 10, 3–9.
29. Brooks, L. R. (1978). Non-analytic concept formation and memory for instances. In E. Rosch & B. B. Lloyd (Eds.), Cognition and categorization (pp. 169–211). Hillsdale, NJ: Erlbaum.
30. Brooks, L. R., Norman, G. R., & Allen, S. W. (1991). Role of specific similarity in a medical diagnostic task. Journal of Experimental Psychology: General, 120, 278–287.
31. Bruner, J. S. (1973). Beyond the information given: Studies in the psychology of knowing. New York: Norton.
32. Bruner, J. S., Goodnow, J. J., & Austin, G. A. (1956). A study of thinking. New York: Wiley.
33. Busemeyer, J. R., & Townsend, J. T. (1993). Decision field theory: A dynamic-cognitive approach to decision making in an uncertain environment. Psychological Review, 100, 432–459.
34. Cabrera, A., & Billman, D. (1996). Language-driven concept learning: Deciphering “Jabberwocky.” Journal of Experimental Psychology: Learning, Memory, and Cognition, 22, 539– 555.
35. Calder, A. J., Young, A. W., Perrett, D. I., Etcoff, N. L., & Rowland, D. (1996). Categorical perception of morphed facial expressions. Visual Cognition, 3, 81–117.
36. Carey, S. (1985). Conceptual change in childhood. Cambridge, MA: Bradford Books.
37. Choi, S., McDaniel, M. A., & Busemeyer, J. R. (1993). Incorporating prior biases in network models of conceptual rule learning. Memory & Cognition, 21, 413–423.
38. Cohen, L. B., & Oakes, L. M. (1993). How infants perceive a simple causal event. Developmental Psychology, 29, 421–433.
39. Crawford, L. J., Huttenlocher, J., & Engebretson, P. H. (2000). Category effects on estimates of stimuli: Perception or reconstruction? Psychological Science, 11, 284–288.
40. Edelman, S. (1998). Representation is representation of similarities. Behavioral and Brain Sciences, 21, 449–498.
41. Edelman, S. (1999). Representation and recognition in vision. Cambridge, MA: Bradford Books/MIT Press.
42. Erickson, M. A., & Kruschke, J. K. (1998). Rules and exemplars in category learning. Journal of Experimental Psychology: General, 127, 107–140.
43. Estes, W. K. (1986). Array models for category learning. Cognitive Psychology, 18, 500–549.
44. Estes, W. K. (1994). Classification and cognition. New York: Oxford University Press.
45. Fodor, J. A. (1975). The language of thought. New York: Thomas Y. Crowell.
46. Fodor, J. A. (1983). The modularity of mind: An essay on faculty psychology. Cambridge, MA: MIT Press.
47. Fodor, J. A., Garrett, M., Walker, E., & Parkes, C. M. (1980). Against definitions. Cognition, 8, 263–367.
48. Fodor, J. A., & Pylyshyn, Z. W. (1988). Connectionism and cognitive architecture: A critical analysis. Cognition, 28, 3–71.
49. Garrod, S., & Doherty, G. (1994). Conversation, co-ordination and convention: An empirical investigation of how groups establish linguistic conventions. Cognition, 53, 181–215.
50. Gelman, S. A., & Markman, E. M. (1986). Categories and induction in young children. Cognition, 23, 183–209.
51. Gentner, D. (1981). Some interesting differences between verbs and nouns. Cognition and Brain Theory, 4, 161–178.
52. Gentner, D. (1982). Why nouns are learned before verbs: Linguistic relativity versus natural partitioning. In S. A. Kuczaj (Ed.), Language development: Vol. 2. Language, thought, and culture (pp. 301–334). Hillsdale, NJ: Erlbaum.
53. Gentner, D., & Boroditsky, L. (2001). Individuation, relativity, and early word learning. In M. Bowerman & S. Levinson (Eds.), Language acquisition and conceptual development (pp. 215– 256). Cambridge, UK: Cambridge University Press.
54. Gluck, M. A., & Bower, G. H. (1988). From conditioning to category learning: An adaptive network model. Journal of Experimental Psychology: General, 117, 227–247.
55. Gluck, M. A., & Bower, G. H. (1990). Component and pattern information in adaptive networks. Journal of Experimental Psychology: General, 119, 105–109.
56. Goldstone, R. L. (1994a). The role of similarity in categorization: Providing a groundwork. Cognition, 52, 125–157.
57. Goldstone, R. L. (1994b). Influences of categorization on perceptual discrimination. Journal of Experimental Psychology: General, 123, 178–200.
58. Goldstone, R. L. (1996). Isolated and Interrelated Concepts. Memory & Cognition, 24, 608–628.
59. Goldstone, R. L. (2000). Unitization during category learning. Journal of Experimental Psychology: Human Perception and Performance, 26, 86–112.
60. Goldstone, R. L., & Barsalou, L. (1998). Reuniting perception and conception. Cognition, 65, 231–262.
61. Goldstone, R. L., & Steyvers, M. (2001). The sensitization and differentiation of dimensions during category learning. Journal of Experimental Psychology: General, 130, 116–139.
62. Goldstone, R. L., Steyvers, M., Spencer-Smith, J., & Kersten, A. (2000). Interactions between perceptual and conceptual learning. In E. Diettrich & A. B. Markman (Eds.), Cognitive dynamics: Conceptual change in humans and machines (pp. 191–228). Mahwah, NJ: Erlbaum.
63. Gopnik, A., & Choi, S. (1995). Names, relational words, and cognitive development in English and Korean speakers: Nouns are not always learned before verbs. In M. Tomasello & W. E. Merriman (Eds.), Beyond names for things: Young children’s acquisition of verbs (pp. 62–94). Hillsdale, NJ: Erlbaum.
64. Grossberg, S. (1982). Processing of expected and unexpected events during conditioning and attention: Apsychophysiological theory. Psychological Review, 89, 529–572.
65. Hampton, J. A. (1987). Inheritance of attributes in natural concept conjunctions. Memory & Cognition, 15, 55–71.
66. Hampton, J. A. (1993). Prototype models of concept representation. In I. V. Mecheln, J. Hampton, R. S. Michalski, & P. Theuns (Eds.), Categories and concepts: Theoretical views and inductive data analysis (pp. 67–95). London: Academic Press.
67. Hampton, J. A. (1997). Conceptual combination: Conjunction and negation of natural concepts. Memory & Cognition, 25, 888– 909.
68. Harnad, S. (1987). Categorical perception. Cambridge, UK: Cambridge University Press.
69. Harnad, S. (1990). The symbol grounding problem. Physica D, 42, 335–346.
70. Harnad, S., Hanson, S. J., & Lubin, J. (1995). Learned categorical perception in neural nets: Implications for symbol grounding. In V. Honavar & L. Uhr (Eds.), Symbolic processors and connectionist network models in artificial intelligence and cognitive modelling: Steps toward principled integration (pp. 191–206). Boston: Academic Press.
71. Heider, E. R. (1972). Universals in color naming and memory. Journal of Experimental Psychology, 93, 10–20.
72. Heit, E. (1994). Models of the effects of prior knowledge on category learning. Journal of Experimental Psychology: Learning, Memory, and Cognition, 20, 1264–1282.
73. Heit, E. (1997). Knowledge and concept learning. In K. Lamberts & D. Shanks (Eds.), Knowledge, concepts, and categories (pp. 7– 41). Hove, UK: Psychology Press.
74. Heit, E. (2000). Properties of inductive reasoning. Psychonomic Bulletin and Review, 7, 569–592.
75. Hintzman, D. L. (1986). “Schema abstraction” in a multiple-trace memory model. Psychological Review, 93, 411–429.
76. Homa, D., & Cultice, J. C. (1984). Role of feedback, category size, and stimulus distortion on the acquisition and utilization of illdefined categories. Journal of Experimental Psychology: Learning, Memory, and Cognition, 10, 234–257.
77. Homa, D., Sterling, S., & Trepel, L. (1981). Limitations of exemplar-based generalization and the abstraction of categorical information. Journal of Experimental Psychology: Human Learning and Memory, 7, 418–439.
78. Hull, C. L. (1920). Quantitative aspects of the evolution of concepts. Psychological Monographs, 28 (Whole No. 123).
79. Hummel, J. E., & Biederman, I. (1992). Dynamic binding in a neural network for shape recognition. Psychological Review, 99, 480–517.
80. Huttenlocher, J., Hedges, L. V., & Vevea, J. L. (2000). Why do categories affect stimulus judgment? Journal of Experimental Psychology: General, 129, 220–241.
81. Huttenlocher, J., & Lui, F. (1979). The semantic organization of some simple nouns and verbs. Journal of Verbal Learning and Verbal Behavior, 18, 141–162.
82. Jones, S. S., & Smith, L. B. (1993). The place of perception in children’s concepts. Cognitive Development, 8, 113–139.
83. Katz, J., & Fodor, J. (1963). The structure of a semantic theory. Language, 39, 170–210.
84. Keil, F. C. (1989). Concepts, kinds and development. Cambridge, MA: Bradford Books/MIT Press.
85. Kersten, A. W. (1998). A division of labor between nouns and verbs in the representation of motion. Journal of Experimental Psychology: General, 127, 34–54.
86. Kersten, A. W., & Billman, D. O. (1997). Event category learning. Journal of Experimental Psychology: Learning, Memory, and Cognition, 23, 638–658.
87. Kolers, P. A., & Roediger, H. L. (1984). Procedures of mind. Journal of Verbal Learning and Verbal Behavior, 23, 425–449. Kohonen, T. (1995). Self-organizing maps. Berlin: Springer-Verlag.
88. Komatsu, L. K. (1992). Recent views of conceptual structure. Psychological Bulletin, 112, 500–526.
89. Knowlton, B. J., & Squire, L. R. (1993). The learning of categories: Parallel brain systems for item memory and category knowledge. Science, 262, 1747–1749.
90. Kruschke, J. K. (1992). ALCOVE: An exemplar-based connectionist model of category learning. Psychological Review, 99, 22–44.
91. Kuhl, P. K., & Miller, J. D. (1975). Speech perception by the chinchilla: Voice-voiceless distinction in alveolar plosive consonants. Science, 190, 69–72.
92. Lakoff, G. (1987). Women, fire and dangerous things: What categories reveal about the mind. Chicago: University of Chicago Press.
93. Lamberts, K. (1998). The time course of categorization. Journal of Experimental Psychology: Learning, Memory, and Cognition, 24, 695–711.
94. Lamberts, K. (2000). Information-accumulation theory of speeded categorization. Psychological Review, 107, 227–260.
95. Landauer, T. K., & Dumais, S. T. (1997). A solution to Plato’s problem: The Latent Semantic Analysis theory of the acquisition, induction, and representation of knowledge. Psychological Review, 104, 211–240.
96. Lassaline, M. E., & Logan, G. D. (1993). Memory-based automaticity in the discrimination of visual numerosity. Journal of Experimental Psychology: Learning, Memory, and Cognition, 19, 561–581.
97. Lenat, D. B., & Feigenbaum, E. A. (1991). On the thresholds of knowledge. Artificial Intelligence, 47, 185–250.
98. Levin, D. T., & Beale, J. M. (2000). Categorical perception occurs in newly learned faces, other-race faces, and inverted faces. Perception & Psychophysics, 62, 386–401.
99. Liberman, A. M., Cooper, F. S., Shankweiler, D. P., & StuddertKennedy, M. (1967). Perception of the speech code. Psychological Review, 74, 431–461.
100. Liberman, A. M., Harris, K. S., Hoffman, H. S., & Griffith, B. C. (1957). The discrimination of speech sounds within and across phoneme boundaries. Journal of Experimental Psychology, 54, 358–368.
101. Logan, G. D. (1988). Toward an instance theory of automatization. Psychological Review, 95, 492–527.
102. Luce, R. D. (1959). Individual choice behavior. New York: Wiley.
103. Maddox, W. T., & Ashby, F. G. (1993). Comparing decision bound and exemplar models of categorization. Perception & Psychophysics, 53, 49–70.
104. Malt, B. C. (1994). Water is not H₂ Cognitive Psychology, 27, 41–70.
105. Marcus, G. F. (1998). Rethinking eliminativist connectionism. Cognitive Psychology, 37, 243–282.
106. Markman, A. B., & Dietrich, E. (2000). In defense of representation. Cognitive Psychology, 40, 138–171.
107. Markman, A. B., & Makin, V. S. (1998). Referential communication and category acquisition. Journal of Experimental Psychology: General, 127, 331–354.
108. Marr, D., & Nishihara, H. K. (1978). Representation and recognition of the spatial organization of three-dimensional shapes. Proceedings of the Royal Society of London, 200B, 269–294.
109. McCloskey, M., & Glucksberg, S. (1978). Natural categories: Well defined or fuzzy-sets? Memory & Cognition, 6, 462–472.
110. McFadden, D., & Callaway, N. L. (1999). Better discrimination of small changes in commonly encountered than in less commonly encountered auditory stimuli. Journal of Experimental Psychology: Human Perception and Performance, 25, 543–560.
111. McKinley, S. C., & Nosofsky, R. M. (1995). Investigations of exemplar and decision bound models in large, ill-defined category structures. Journal of Experimental Psychology: Human Perception and Performance, 21, 128–148.
112. McNamara, T. P, & Miller, D. L. (1989). Attributes of theories of meaning. Psychological Bulletin, 106, 355–376.
113. Medin, D. L. (1989). Concepts and conceptual structure. American Psychologist, 44, 1469–1481.
114. Medin, D. L., & Atran, S. (1999). Cambridge, MA: MIT Press.
115. Medin, D. L., Dewey, G. I., & Murphy, T. D. (1983). Relationships between item and category learning: Evidence that abstraction is not automatic. Journal of Experimental Psychology: Learning, Memory, and Cognition, 9, 607–625.
116. Medin, D. L., Lynch. E. B., & Solomon, K. O. (2000). Are there kinds of concepts? Annual Review of Psychology, 51, 121–147.
117. Medin, D. L., & Schaffer, M. M. (1978). Context theory of classification learning. Psychological Review, 85, 207–238.
118. Medin, D. L., & Shoben, E. J. (1988). Context and structure in conceptual combination. Cognitive Psychology, 20, 158–190.
119. Medin, D. L., & Smith, E. E. (1984). Concepts and concept formation. Annual Review of Psychology, 35, 113–138.
120. Medin, D. L., Wattenmaker, W. D., & Michalski, R. S. (1987). Constraints and pBibliography: in inductive learning: An experimental study of human and machine performance. Cognitive Science, 11, 299–339.
121. Mervis, C. B., & Rosch, E. (1981). Categorization of natural objects. Annual Review of Psychology, 32, 89–115.
122. Miyawaki, K. (1975). An effect of linguistic experience. The discrimination of (r) and (l) by native speakers of Japanese and English. Perception & Psychophysics, 18, 331–340.
123. Murphy, G. L. (1988). Comprehending complex concepts. Cognitive Science, 12, 529–562.
124. Murphy, G. L., & Allopenna, P. D. (1994). The locus of knowledge effectsincategorylearning.JournalofExperimentalPsychology: Learning, Memory, and Cognition, 20, 904–919.
125. Murphy, G. L., & Kaplan, A. S. (2000). Feature distribution and background knowledge in category learning. Quarterly Journal of Experimental Psychology: Human Experimental Psychology, 53A, 962–982.
126. Murphy, G. L., & Medin, D. L. (1985). The role of theories in conceptual coherence. Psychological Review, 92, 289–316.
127. Naigles, L. R., & Terrazas, P. (1998). Motion-verb generalizations in English and Spanish: Influences of language and syntax. Psychological Science, 9, 363–369.
128. Nosofsky, R. M. (1984). Choice, similarity, and the context theory of classification. Journal of Experimental Psychology: Learning, Memory, and Cognition, 10, 104–114.
129. Nosofsky, R. M (1986). Attention, similarity, and the identificationcategorization relationship. Journal of Experimental Psychology: General, 115, 39–57.
130. Nosofsky, R. M. (1992). Similarity scaling and cognitive process models. Annual Review of Psychology, 43, 25–53.
131. Nosofsky, R. M., Kruschke, J. K., & McKinley, S. C. (1992). Combining exemplar-based category representations and connectionist learning rules. Journal of Experimental Psychology: Learning, Memory, and Cognition, 18, 211–233.
132. Nosofsky, R. M., & Palmeri, T. J. (1998). A rule-plus-exception model for classifying objects in continuous-dimension spaces. Psychonomic Bulletin and Review, 5, 345–369.
133. Nosofsky, R. M., Palmeri, T. J., & McKinley, S. K. (1994). Ruleplus-exception model of classification learning. Psychological Review, 101, 53–79.
134. Oaksford, M., & Chater, N. (1998). Rationality in an uncertain world: Essays on the cognitive science of human reasoning. Hove, UK: Psychology Press/Erlbaum.
135. O’Toole, A. J., Peterson, J., & Deffenbacher, K. A. (1995). An ‘other-race effect’ for categorizing faces by sex. Perception, 25, 669–676.
136. Palmeri, T. J. (1997). Exemplar similarity and the development of automaticity. Journal of Experimental Psychology: Learning, Memory, and Cognition, 23, 324–354.
137. Palmeri, T. J., & Nosofsky, R. M. (1995). Recognition memory for exceptions to the category rule. Journal of Experimental Psychology: Learning, Memory, and Cognition, 21, 548–568.
138. Pastore, R. E. (1987). Categorical perception: Some psychophysical models. In S. Harnad (Ed.), Categorical perception (pp. 29–52). Cambridge, UK: Cambridge University Press.
139. Pazzani, M. J. (1991). Influence of prior knowledge on concept acquisition: Experimental and computational results. Journal of Experimental Psychology: Learning, Memory, and Cognition, 17, 416–432.
140. Perrett, D. I., Oram, M. W., & Ashbridge, E. (1998). Evidence accumulation in cell populations responsive to faces: An account of generalization of recognition without mental transformations. Cognition, 67, 111–145.
141. Piaget, J. (1952). The origins of intelligence in children. New York: International Universities Press.
142. Pinker, S. (1991). Rules of language. Science, 253, 530–535.
143. Pinker, S. (1994). The language instinct. New York: W. Morrow.
144. Posner, M. I., & Keele, S. W. (1967). Decay of visual information from a single letter. Science, 158, 137–139.
145. Posner, M. I., & Keele, S. W. (1968). On the genesis of abstract ideas. Journal of Experimental Psychology, 77, 353–363.
146. Posner, M. I., & Keele, S. W. (1970). Retention of abstract ideas. Journal of Experimental Psychology, 83, 304–308.
147. Repp, B. H., & Liberman, A. M. (1987). Phonetic category boundaries are flexible. In S. R. Harnad (Ed.), Categorical perception (pp. 89–112). New York: Cambridge University Press.
148. Ripley, B. D. (1996). Pattern recognition and neural networks. Cambridge, UK: Cambridge University Press.
149. Rips, L. J. (1975). Inductive judgments about natural categories. Journal of Verbal Learning and Verbal Behavior, 14, 665–681.
150. Rips, L. J. (1989). Similarity, typicality, and categorization. In S. Vosniadu & A. Ortony (Eds.), Similarity, analogy, and thought (pp. 21–59). Cambridge, UK: Cambridge University Press.
151. Rips, L. J., & Collins, A. (1993). Categories and resemblance. Journal of Experimental Psychology: General, 122, 468–486.
152. Roberson, D., Davies, I., & Davidoff, J. (2000). Color categories are not universal: Replications and new evidence from a stone-age culture. Journal of Experimental Psychology: General, 129, 369–398.
153. Rosch, E. (1975). Cognitive representations of semantic categories. Journal of Experimental Psychology: General, 104, 192–232.
154. Rosch, E., & Mervis, C. B. (1975). Family resemblances: Studies in the internal structure of categories. Cognitive Psychology, 7, 573–605.
155. Rosch, E., Mervis, C. B., Gray, W., Johnson, D., & Boyes-Braem, P. (1976). Basic objects in natural categories. Cognitive Psychology, 8, 382–439.
156. Ross, B. H., & Murphy, G. L. (1999). Food for thought: Crossclassification and category organization in a complex real-world domain. Cognitive Psychology, 38, 495–553.
157. Rumelhart, D. E., & Zipser, D. (1985). Feature discovery by competitive learning. Cognitive Science, 9, 75–112.
158. Schank, R. C. (1982). Dynamic memory: A theory of reminding and learning in computers and people. Cambridge, UK: Cambridge University Press.
159. Schusterman, R. J., Reichmuth, C. J., & Kastak, D. (2000). How animals classify friends and foes. Current Directions in Psychological Science, 9, 1–6.
160. Schyns, P. G. (1998). Diagnostic recognition: Task constraints, object information, and their interactions. Cognition, 67, 147– 179.
161. Shanks, D. R. (1991). Categorization by a connectionist network. Journal of Experimental Psychology: Learning, Memory, and Cognition, 17, 433–443.
162. Shin, H. J., & Nosofsky, R. M. (1992). Similarity-scaling studies of dot-pattern classification and recognition. Journal of Experimental Psychology: General, 121, 278–304.
163. Sidman, M. (1994). Equivalence relations and behavior: A research story. Boston: Authors.
164. Sloman, S. A. (1996). The empirical case for two systems of reasoning. Psychological Bulletin, 119, 3–22.
165. Sloman, S. A., Love, B. C., & Ahn, W.-K. (1998). Feature centrality and conceptual coherence. Cognitive Science, 22, 189–228.
166. Smith, E. E. (1989). Concepts and induction. In M. I. Posner (Ed.), Foundations of cognitive science (pp. 501–526). Cambridge, MA: MIT Press.
167. Smith, E. E., Langston, C., & Nisbett, R. (1992). The case for rules in reasoning. Cognitive Science, 16, 1–40.
168. Smith, E. E., & Medin, D. L. (1981). Categories and concepts. Cambridge, MA: Harvard University Press.
169. E. E., Patalano, A. L., & Jonides, J. (1998). Alternative strategies of categorization. Cognition, 65, 167–196.
170. Smith, E. E., Shoben, E. J., & Rips, L. J. (1974). Structure and process in semantic memory: A featural model for semantic decisions. Psychological Review, 81, 214–241.
171. Smith, E. E., & Sloman, S. A. (1994). Similarity- versus rule-based categorization. Memory & Cognition, 22, 377–386.
172. Smith, J. D., & Minda, J. P. (2000). Thirty categorization results in search of a model. Journal of Experimental Psychology: Learning, Memory, and Cognition, 26, 3–27.
173. Smith,L.B.(1999).Children’snounlearning:Howgeneralprocesses make specialized learning mechanisms. In B. MacWhinney (Ed.), The emergence of language (pp. 277–304). Mahwah, NJ: Erlbaum.
174. Snodgrass, J. G. (1984). Concepts and their surface representations. Journal of Verbal Learning and Verbal Behavior, 23, 3–22.
175. Solomon, K., & Barsalou, L. W. (1999). Grounding concepts in perceptual simulation: Vol. 2. Evidence from property verification. Manuscript submitted for publication.
176. Spalding, T. L., & Murphy, G. L. (1999). What is learned in knowledge-related categories? Evidence from typicality and feature frequency judgments. Memory & Cognition, 27, 856–867.
177. Storms, G., De Boeck, P., Hampton, J. A., & Van Mechelen, I. (1999). Predicting conjunction typicalities by component typicalities. Psychonomic Bulletin and Review, 6, 677–684.
178. Talmy, L. (1985). Lexicalization patterns: Semantic structure in lexical forms. In T. Shopen (Ed.), Language typology and syntactic description: Vol. 3. Grammatical categories and the lexicon (pp. 97–149). New York: Cambridge University Press.
179. Tardif, T. (1996). Nouns are not always learned before verbs: Evidence from Mandarin speakers’ early vocabularies. Developmental Psychology, 32, 492–504.
180. Tanaka, J., & Taylor, M. (1991). Object categories and expertise: Is the basic level in the eye of the beholder? Cognitive Psychology, 23, 457–482.
181. Tarr, M. J., & Bülthoff, H. H. (1995). Is human object recognition better described by geon-structural-descriptions of by multipleviews? Journal of Experimental Psychology: Human Perception and Performance, 21, 1494–1505.
182. Tarr, M. J., & Gauthier, I. (1998). Do viewpoint-dependent mechanisms generalize across members of a class? Cognition, 67, 73–110.
183. Tennenbaum, J. B. (1999). Bayesian modeling of human concept learning. Advances in Neural Information Processing Systems, 11, 251–257.
184. Thelen, E., & Smith, L. B. (1994). A dynamic systems approach to the development of cognition and action. Cambridge, MA: MIT Press. van Gelder, T. (1998). The dynamical hypothesis in cognitive science. Behavioral and Brain Sciences, 21, 615–665.
185. Werker, J. F., & Tees, R. C. (1984). Cross-language speech perception: Evidence for perceptual reorganization during the first year of life. Infant Behavior and Development, 7, 49–63.
186. Whorf, B. L. (1956). The relation of habitual thought and behavior to language. In J. B. Carroll (Ed.), Language, thought, and reality: Essays by B. L. Whorf (pp. 35–270). Cambridge, MA: MIT Press.
187. Wisniewski, E. J. (1997). When concepts combine. Psychonomic Bulletin and Review, 4, 167–183.
188. Wisniewski, E. J. (1998). Property instantiation in conceptual combination. Memory & Cognition, 26, 1330–1347.
189. Wisniewski, E. J., & Love, B. C. (1998). Relations versus properties in conceptual combination. Journal of Memory and Language, 38, 177–202.
190. Wittgenstein, L. (1953). Philosophical investigations (G. E. M. Anscombe, Trans.). New York: Macmillan.
191. Wolff, P., Medin, D. L., & Pankratz, C. (1999). Evolution and devolution of folkbiological knowledge. Cognition, 73, 177–204.