Reasoning and Problem Solving Research Paper

How did Oedipus solve a problem that had led so many to an early grave? Is there any purpose in knowing that he solved the problem by inferring the conclusion, applying a strategy, or experiencing an insight into its resolution? Knowing how Oedipus arrived at his answer might have saved the men before him from death as sphinx fodder. Most of the problems that we face in everyday life are not as menacing as the one Oedipus faced that day. Nevertheless, the conditions under which Oedipus resolved the riddle correspond in some ways to the conditions of our own everyday problems: Everyday problems are solved with incomplete information and under time constraints, and they are subject to meaningful consequences. For example, imagine you need to go pick up a friend from a party and you realize that a note on which you wrote the address is missing. How would you go about recovering the address or the note on which you wrote the address without being late? If there is a way to unlock the mysteries of thinking and secure clever solutions—to peer inside Oedipus’s mind—then we might learn to negotiate answers in the face of uncertainty.

It might be possible to begin unraveling Oedipus’s solution by considering how Oedipus approached the riddle; that is, did he approach the riddle as a reasoning task, in which a conclusion needed to be deduced, or did he approach the riddle as a problem-solving task, in which a solution needed to be found? Is there any purpose in distinguishing between the processes of reasoning and problem solving in considering how Oedipus solved the riddle? There is some purpose in distinguishing these processes, at least at the outset, because psychologists believe that these operations are relatively distinct (Galotti, 1989). Reasoning is commonly defined as the process of drawing conclusions from principles and from evidence (Wason & Johnson-Laird, 1972). In contrast, problem solving is defined as the goal-driven process of overcoming obstacles that obstruct the path to a solution (Simon, 1999a; Sternberg, 1999). Given these definitions, would it be more accurate to say that Oedipus resolved the riddle by reasoning or by problem solving? Knowing which operation he used might help us understand which operations we should apply to negotiate our own answers to uncertain problems.

Unfortunately, we cannot peer inside the head of the legendary Oedipus, and it is not immediately obvious from these definitions which one—the definition of reasoning or that of problem solving—describes the set of processes leading to his answer. If we are to have any hope of understanding how Oedipus negotiated a solution to the riddle and how we might negotiate answers to our own everyday riddles, then we must examine reasoning and problem solving more closely for clues.

Goals of This Research Paper

The goals of the present research paper are to cover what is known about reasoning and problem solving, what is currently being done, and in what directions future conceptualizations, research, and practice are likely to proceed. We hope through the paper to convey an understanding of how reasoning and problem solving differ from each other and how they resemble each other. In addition, we hope that we can apply what we have learned to determine whether the sphinx’s riddle was essentially a reasoning task or a problem-solving task, and whether knowing which one it was helps us understand how Oedipus solved it.

Reasoning

During the last three decades, investigators of reasoning have advanced many different theories (see Evans, Newstead, & Byrne, 1993, for a review). The principal theories can be categorized as rule theories (e.g., Cheng & Holyoak, 1985; Rips, 1994), semantic theories (e.g., Johnson-Laird, 1999; Polk & Newell, 1995), and evolutionary theories (e.g., Cosmides, 1989). These theories advance the idea of a fundamental reasoning mechanism (Roberts, 1993, 2000), a hardwired or basic mechanism that controls most, if not all, kinds of reasoning (Roberts, 2000). In addition, some investigators have proposed heuristic theories of reasoning, which do not claim a fundamental reasoning mechanism but, instead, claim that simple strategies govern reasoning. Sometimes these simple strategies lead people to erroneous conclusions, but, most of the time, they help people draw adequate conclusions in everyday life. According to rule theorists, semantic theorists, and evolutionary theorists, however, reasoning is better described as a basic mechanism that, if unaltered, should always lead to correct inferences.

Rule Theories

Supporters of rule theories believe that reasoning is characterized by the use of specific rules or commands. Competent reasoning is characterized by applying rules properly, by using the appropriate rules, and by implementing the correct sequence of rules (Galotti, 1989; Rips, 1994). Although the exact nature of the rules might change depending on the specific rule theory considered, all rules are normally expressed as propositional commands such as (antecedent or premise) → (consequent or conclusion). If a reasoning task matches the antecedent of the rule, then the rule is elicited and applied to the task to draw a conclusion. Specific rule theories are considered below.

Syntactic Rule Theory

According to syntactic rule theory, people draw conclusions using formal rules that are based on natural deduction and that can be applied to a wide variety of situations (Braine, 1978; Braine & O’Brien, 1991, 1998; Braine & Rumain, 1983; Rips, 1994, 1995; Rumain, Connell, & Braine, 1983). Reasoners are able to use these formal rules by extracting the logical forms of premises and then applying the rules to these logical forms to derive conclusions (Braine & O’Brien, 1998).

For example, imagine Oedipus trying to answer the sphinx’s riddle, which makes reference to something walking on two legs. In trying to make sense of the riddle, Oedipus might have remembered an old rule stating that If it walks on two legs, then it is a person. Combining part of the riddle with his old rule, Oedipus might have formed the following premise set in his mind:

If it walks on two legs, then it is a person.            (Oedipus’ rule A)

                                                                                                       (1)

It walks on two legs. (Part of riddle)

Therefore ?

The conclusion to the above premise set can be inferred by applying a rule of logic, modus ponens, which eliminates the if, as follows:

If A then B.

A.

Therefore B.

Applying the modus ponens rule to premise set (1) would have allowed Oedipus to conclude “person.”

Another feature of syntactic theory is the use of suppositions, which involve assuming additional information for the sake of argument. A supposition can be paired with other premises to show that it leads to a contradiction and, therefore, must be false. For example, consider the following premise set:

1. If it walks on three legitimate legs, then it is not a person. (Oedipus’ rule B) (2)
2. It is a person. (Conclusion from premise set (1) above)
3. It walks on three legitimate legs. ( A supposition)
4. Therefore it is not a person (Modus ponens applied to a and c)

As can be seen from premise set (2), there is a contradiction between the premise It is a person and the conclusion derived from the supposition, It is not a person. According to the rule of reductio ad absurdum, because the supposition leads to a contradiction, the supposition must be negated. In other words, we reject that it walks on three legitimate legs. Because this so-called modus tollens inference is not generated as simply as is the modus ponens inference, syntactic rule theorists propose that the modus tollens inference relies on a series of inferential steps, instead of on the single step associated with modus ponens. If Oedipus considered the line of argument above, it might have led him to reject the possibility that the sphinx’s riddle referred to anything with three legitimate legs.

In an effort to validate people’s use of reasoning rules, Braine, Reiser, and Rumain (1998) conducted two studies. In one of their studies, 28 participants were asked to read 85 reasoning problems and then to evaluate the conclusion presented with each problem. Some problems were predicted to require the use of only one rule for their evaluation (e.g., There is an O and a Z; There is an O?), whereas other problems were predicted to require the use of multiple rules or deductive steps for their evaluation (e.g., There is an F or a C; If there’s not an F, then there is a C?). Participants were asked to evaluate the conclusions by stating whether the proposed conclusion was true, false, or indeterminate. The time taken by each participant to evaluate the conclusion was measured. In addition, after solving each problem, participants were asked to rate the difficulty of the problem using a 9-point scale, with 1 indicating a very easy problem and 9 indicating a very difficult problem. These difficulty ratings were then used to estimate difficulty weights for the reasoning rules assumed to be involved in evaluating the problems. The estimated difficulty weights were then used to predict how another group of participants in a similar study rated a set of new reasoning problems. Braine et al. (1998) found that the difficulty weights could be used to predict participants’ difficulty ratings in the similar study with excellent accuracy (correlations ranged up to .95). In addition, the difficulty weights predicted errors and latencies well; long reaction times and inaccurate performance indicated people’s attempts to apply difficult and long rule routines, whereas short reaction times and accurate performance indicated people’s attempts to apply easy and short rule routines (see also Rips, 1994). Braine et al. (1998) concluded from these results that participants do in fact reason using the steps proposed by the syntactic theory of mental-propositional logic. Outside of these results, other investigators have also found evidence of rule use (e.g., Ford, 1995; Galotti, Baron, & Sabini, 1986; Torrens, Thompson, & Cramer, 1999).

Supporters of syntactic theory use formal or logical reasoning tasks in their investigations of reasoning rules. According to syntactic theorists, errors in reasoning arise because people apply long rule routines incorrectly or draw unnecessary invited conclusions from the task information. Invited, or simply plausible (but not logically certain), conclusions can be drawn in everyday discourse but are prohibited on formal reasoning tasks, in which information must be interpreted in a strictly logical manner. Because the rules in syntactic theory are used to draw logically certain conclusions, critics of the theory maintain that these rules appear unsuitable for reasoning in everyday situations, in which information is ambiguous and uncertain and additional information must be considered before any reasonable conclusion is likely to be drawn. In defense of the rule approach, it is possible that people unknowingly interject additional information in order to make formal rules applicable. However, it is unclear how one would know what kind of additional information to include. Dennett (1990) has described the uncertainty of what additional information to consider as the frame problem (see also Fodor, 1983).

The frame problem involves deciding which beliefs from a multitude of different beliefs to consider when solving a task or when updating beliefs after an action has occurred (Dennett, 1990; Fodor, 1983). The ability to consider different beliefs can lead to insightful and creative comparisons and solutions, but it also raises the question: How do human beings select from among all their beliefs those that are relevant to generating a conclusion in a reasoning problem? The frame problem is a perplexing issue that has not been addressed by syntactic rule theorists.

If it were possible to ask Oedipus how he reached the answer to the riddle, would he be able to say how he did it? That is, could he articulate that he used a rule of some sort to generate his conclusion, or would this knowledge be outside of his awareness? This question brings up a fundamental issue that arises when discussing theories of reasoning: Is the theory making a claim about the strategies that a person in particular might use in reasoning or about something more basic, such as how the mind in general processes information, that is, the mind’s cognitive architecture (Dawson, 1998; Johnson-Laird, 1999; Newell, 1990; Rips, 1994)? The mind’s cognitive architecture is thought to lie outside conscious awareness because it embodies the most basic non-physical description of cognition—the fundamental information processing steps underlying cognition (Dawson, 1998; Newell, 1990). In contrast, strategies are thought to be accessible to conscious awareness (Evans, 2000).

Some theories of reasoning seem to pertain to the nature of the mind’s cognitive architecture. For example, Rips (1994) has proposed a deduction-system hypothesis, according to which formal rules do not underlie only deductive reasoning, or even only reasoning in general, but also the mind’s cognitive architecture. He argues that his theory of rules can be used as a programming language of general cognitive functions, for example, to implement a production system: a routine that controls cognitive actions by determining whether the antecedents for the cognitive actions have been satisfied (Simon, 1999b; see below for a detailed definition of production systems). The problem with this claim is that production systems have already been proposed as underlying the cognitive architecture and as potentially used to derive syntactic rules (see Eisenstadt & Simon, 1997). Thus, it is not clear which is more fundamental: the syntactic rules or the production systems. Claims have been staked according to which each derives from the other, but both sets of claims cannot be correct.

Another concern with Rips’s (1994) deductive-system hypothesis is that its claim about the mind’s cognitive architecture is based on data obtained from participants’performance on reasoning tasks, tasks that are used to measure controlled behaviors. Controlled behavior, according to Newell (1990), is not where we find evidence for the mind’s architecture, because this behavior is slow, load-dependent, and open to awareness; it can be inhibited; and it permits self-terminating search processes. In contrast, immediate behavior (e.g., as revealed in choice reaction tasks) “is the appropriate arena in which to discover the nature of the cognitive architecture” (Newell, 1990, p. 236). The swiftness of immediate, automatic responses exposes the mind’s basic mechanism, which is revealed in true form and unregulated by goal-driven adaptive behavior.

Determining at what level a theory is intended to account for reasoning is important in order to assess the evidence presented as support for the theory. If syntactic rule theory is primarilyatheoryofthemind’scognitivearchitecture,thenwe would not think, for example, of asking Oedipus to think aloud as to how he solved the riddle in an effort to confirm syntactic ruletheory.Think-aloudreportswouldbeinadequateevidence in support of the theory. Our question would be fruitless because, although Oedipus might be able to tell us about the strategies he used and the information he thought about in solving the riddle, he presumably would not be able to tell us about his cognitive architecture; he would not have access to it.

Pragmatic Reasoning Theory

Another theory that invokes reasoning rules is pragmatic reasoning theory (Cheng & Holyoak, 1985, 1989; Cheng & Nisbett, 1993). Pragmatic reasoning theorists suggest that people reason by mapping the information they are reasoning about to information they already have stored in memory. In particular, these theorists suggest that this mapping is accomplished by means of schemas, which consist of sets of rules related to achieving particular kinds of goals for reasoning in specific domains.

Cheng and Holyoak (1985) have proposed that in domains where permission and obligation must be negotiated, we activate a permission schema to help us reason. The permission schema is composed of four production rules, “each of which specifies one of the four possible antecedent situations, assuming the occurrence or nonoccurrence of the action and precondition” (p. 396). The four possible antecedent situations along with their corresponding consequences are shown below:

Rule 1: If the action is to be taken, then the precondition must be satisfied.

Rule 2: If the action is not to be taken, then the precondition need not be satisfied.

Rule 3: If the precondition is satisfied, then the action may be taken.

Rule 4: If the precondition is not satisfied, then the action must not be taken.

To understand how these rules are related to reasoning, we first need to discuss how pragmatic reasoning theory grew out of tests of the Wason selection task (Wason, 1966). The selection task is a hypothesis-testing task in which participants are given a conditional rule of the form If Pthen Q and four cards, each of which has either a Por a not-P on one side and either a Q or a not-Q on the other side.As shown in Figure 23.1, each of the cards is placed face down so that participants can see only one side of a given card. After participants read the conditional rule, they are asked to select the cards that test the truth or falsity of the rule. According to propositional logic, only two cards can conclusively test the conditional rule: The P card can potentially test the truth or falsity of the rule because when flipped it might have a not-Q on its other side, and the not-Q card can test the rule because when flipped it might have a P on its other side. The actual conditional rule used in the Wason selection task is If there is a vowel on one side of the card, then there is an even number on the other side of the card, and the actual cards shown to participants have an exemplar of either a vowel or a consonant on one side and an even number or an odd number on the other side.As few as 10% of participants choose both the P and not-Q cards (the logically correct cards), with many more participants choosing either the P card by itself or both the P and Q cards (Evans & Lynch, 1973; Wason, 1966, 1983; Wason & Johnson-Laird, 1972; for a review of the task see Evans, Newstead, et al., 1993).

Cheng and Holyoak (1985, 1989) have argued that people perform poorly on the selection task because it is too abstract and not meaningful. Their pragmatic reasoning theory grew out of studies showing that it was possible to improve significantly participants’ performance on the selection task by using a meaningful, concrete scenario involving permissions and obligations. Permission is defined by Cheng and Holyoak (1985) as a regulation in which, in order to undertake a particular action, one first must fulfill a particular precondition. An obligation is defined as a regulation in which a situation requires the execution of a subsequent action. In a test of pragmatic reasoning theory, Cheng and Holyoak (1985) presented participants with the following permission scenario as an introduction to the selection task:

You are an immigration officer at the International Airport in Manila, capital of the Philippines. Among the documents you must check is a sheet called Form H. One side of this form indicates whether the passenger is entering the country or in transit, and the other side of the form lists inoculations the passenger has had in the past 6 months.You must make sure that if the form says ENTERING on one side, then the other side includes cholera among the list of diseases. This is to ensure that entering passengers are protected against the disease. Which of the following forms would you have to turn over to check? (pp. 400–401)

The above introduction was followed by depictions of four cards in a fashion similar to that shown in Figure 23.1. The first card depicted the word TRANSIT, another card depicted the word ENTERING, a third card listed the diseases “cholera, typhoid, hepatitis,” and a fourth card listed the diseases “typhoid, hepatitis.” Table 23.1 shows that participants were significantly more accurate in choosing the correct alternatives, P and not-Q, for the permission task (62 %) than for the abstract version of the task (11%). In addition, Table 23.1 indicates that the effect of the permission context generalized across corresponding connective forms; that is, participants’ performance improved not only for permission rules containing the connective if . . . then, but also for permission rules containing the equivalent connective only if.

According to Cheng and Holyoak (1985), the permission schema’s production rules,

• If the action is to be taken, then the precondition must be satisfied; and
• If the pre-condition is not satisfied, then the action must not be taken,

guided participants’correct selection of cards by highlighting the cases where the action was taken (i.e., if the person is entering, then the person must have been inoculated against cholera) and where the precondition was not satisfied (i.e., if the person has not been inoculated, then the person must not enter). According to the theory, reasoning errors occur when a task’s content fails to elicit an appropriate pragmatic reasoning schema. The content of the task must be meaningful and not arbitrary, however; otherwise, participants perform as poorly on concrete as on abstract versions of the selection task (e.g., Manktelow & Evans, 1979).

Despite its success in improving performance on the selection task, pragmatic reasoning theory has been criticized on a number of grounds. For instance, some investigators have charged that pragmatic reasoning schemas are better conceptualized as an undeveloped collection of deontic rules, which are invoked in situations calling for deontic reasoning. Manktelow and Over (1991) describe deontic reasoning as reasoning about what we are allowed to do or what we should do instead of what is actually the case. In other words, deontic reasoning involves reasoning about permissions and obligations. Deontic reasoning is moderated by subtle considerations of semantic, pragmatic, and social information that influence a person’s assessment of the utilities of possible actions. Assessing the utilities of possible actions involves thinking about whether pursuing an action will lead to a desired goal (i.e., does the action have utility for me?) and whether it is justifiable to pursue the action given the value of the outcome. Manktelow and Over (1991) have suggested that although Cheng and Holyoak’s (1985, 1989) schemas are deontic in character, they fail to include how people assess utilities when reasoning about permissions. Furthermore, they have pointed out that the very production rules that make up the permission schema incorporate deontic terms such as may and must that need to be decoded by a more basic schema that deciphers deontic terms.

Other critics of pragmatic reasoning theory have also claimed that the theory is too closely connected with a single task to offer an account of human reasoning generally (e.g., Rips, 1994). Although pragmatic reasoning schemas have been used to explain reasoning about permissions, obligations, and causes and effects, it is unclear if equivalent schemas, whatever form they might take, can also be used to explain other forms of reasoning, such as reasoning about classes or spatial relationships (Liberman & Klar, 1996). The ambiguity of how pragmatic reasoning schemas are applied in unusual or novel situations is one reason why, for example, it is unlikely that Oedipus reasoned according to pragmatic reasoning theory in deriving a conclusion to the sphinx’s riddle. The riddle represents an unusual problem, one for which a schema might not even exist. In addition, even if it were possible to map the riddle’s information onto a schema, how would the schema be selected from the many other schemas in the reasoner’s repertoire?

Finally, although Cheng and Holyoak (1985, 1989) have described how the permission schema helps reasoners infer conclusions in situations involving permissions (see paragraph above), they do not specify how reasoners actually implement the schemas. Schemas serve to represent or organize declarative knowledge, but how does someone proceed from having this representational scheme to knowing when and how to apply it? Does application happen automatically, or is it under our control? If it is under our control, then it seems critical to explore the strategies that people use in deciding to apply a schema. If it is not under our control, then what are the processes by which ineffective schemas are disregarded in the search for the proper schema? The latter issue of how schemas are applied and disregarded is another example of the frame problem (Dennett, 1990). The frame problem in this case involves deciding which schemas—from a possible multitude of schemas—to consider when solving a task.

Semantic Theories

Unlike rule theories, in which reasoning is characterized as resulting from the application of specific rules or commands, semantic theories characterize reasoning as resulting from the particular interpretations assigned to specific assertions. Rules are not adopted in semantic theories because reasoning is thought to depend on the meaning of assertions and not on the syntactic form of assertions.

Mental Model Theory

According to the theory of mental models, reasoning is based on manipulating meaningful concrete information, which is representative of the situations around us, and is not based on deducing conclusions by means of abstract logical forms that are devoid of meaning (Johnson-Laird, 1999). Two mental model theorists, Phil Johnson-Laird and Ruth Byrne (1991), have proposed a three-step procedure for drawing necessary inferences: First, the reasoner constructs an initial model or representation that is analogous to the state of affairs (or information) being reasoned about (Johnson-Laird, 1983). For example, consider that a reasoner is given a conditional rule If there is a circle then there is a square plus an assertion There is a circle and is asked then to draw a conclusion. The initial model or representation he or she might construct for the conditional would likely include the salient cases of the conditional, namely a circle and a square, as follows:

                                                                  ❍ ❑

The reasoner might also recognize the possibility that the antecedent of the conditional (i.e., If there is a circle) could be false, but this possibility would not be normally represented explicitly in the initial model. Rather, this possibility would be represented implicitly in another model, whose presence is defined by an ellipsis attached to the explicit model as follows:

                                                                  ❍ ❑

                                                                          . . .

The second step in the procedure involves drawing a conclusion from the initial model. For example, from the foregoing initial model of the rule, If there is a circle then there is a square, and the assertion, There is a circle, the reasoner can conclude immediately that there is a square alongside the circle. Third, in some cases, the reasoner constructs alternative models of the information in order to verify (or disprove) the conclusion drawn (Johnson-Laird, 1999; Johnson-Laird & Byrne, 1991). For example, suppose that the reasoner had been given a different assertion, such as that There is not a circle in addition to the rule If there is a circle then there is a square. This time, in order to verify the conclusion to be drawn from the conditional rule plus this new assertion, the reasoner would need to flesh out the implicit model indicated in the ellipsis of the initial model. For example, according to a material implication interpretation of the conditional rule, he or she would need to flesh out the implicit model as follows:

                                                                  ~ ❍       ❑

                                                                  ~ ❍     ~❑

where ~ refers to negation.

By using the fleshed out model above, the reasoner would be able to conclude that there is no definite conclusion to be drawn about the presence or absence of a square given the assertion There is not a circle and the rule If there is a circle then there is a square. There is no definite conclusion that can be drawn because in the absence of a circle (i.e., ~ ❍), a square may or may not also be absent. The first two steps in mental model theory—the construction of an initial explicit model and the generation of a conclusion—involve primarily comprehension processes. The third step, the search for alternative models or the fleshing out of the implicit model, defines the process of reasoning (Evans, Newstead, et al., 1993; Johnson-Laird & Byrne, 1991).

The theory of mental models can be further illustrated with categorical syllogisms, which form a standard task used in reasoning experiments (e.g., Johnson-Laird, 1994; Johnson-Laird & Bara, 1984; Johnson-Laird & Byrne, 1991; Johnson-Laird, Byrne, & Schaeken, 1992). Categorical syllogisms consist of two quantified premises and a quantified conclusion. The premises reflect an implicit relation between a subject (S) and a predicate (P) via a middle term (M), whereas the conclusion reflects an explicit relation between the subject (S) and predicate (P). The set of statements below is an example of a categorical syllogism.

ALL S are M

ALL M are P

ALL S are P

Each of the premises and the conclusion in a categorical syllogism takes on a particular form or mood such as All S are M, Some S are M, Some S are not M, or No S are M. The validity of syllogisms can be proven using either prooftheoretical methods or, more commonly, a model-theoretical method. According to the model-theoretical method, a valid syllogism is one whose premises cannot be true without its conclusion also being true (Garnham & Oakhill, 1994). The validity of syllogisms can also be defined using proof-theoretical methods that involve applying rules of inference in much the same way as one would in formulating a mathematical proof (see Chapter 4 in Garnham & Oakhill, 1994, for a detailed description of proof-theoretical methods).

Mental model theory has been used successfully to account for participants’performance on categorical syllogisms (Evans, Handley, Harper, & Johnson-Laird, 1999; JohnsonLaird & Bara, 1984; Johnson-Laird & Byrne, 1991). A number of predictions derived from the theory have been tested and observed. For instance, one prediction suggests that participants should be more accurate in deriving conclusions from syllogisms that require the construction of only a single model than from syllogisms that require the construction of multiple models for their evaluation. An example of a singlemodel categorical syllogism is shown below:

Syllogism:             ALL S are M

                            ALL M are P

                            ALL S are P

       Model:          S = M = P

where = refers to an identity function.

In contrast, a multiple-model syllogism requires that participants construct at least two models of the premises in order to deduce a valid conclusion or determine that a valid conclusion cannot be deduced. Johnson-Laird and Bara (1984) tested the prediction that participants should be more accurate in deriving conclusions from single-model syllogisms than from multiple-model syllogisms by asking 20 untrained volunteers to make an inference from each of 64 pairs of categorical premises randomly presented. The 64 pairs of premises included single-model and multiple-model problems. An analysis of participants’ inferences revealed that valid conclusions declined significantly as the number of models that needed to be constructed to derive a conclusion increased (Johnson-Laird & Bara, 1984, Table 6). Although numerous studies have shown that performance on multiplemodel categorical syllogisms is inferior to performance on single-model categorical syllogisms, Greene (1992) has suggested that inferior performance on multiple-model syllogisms may have little to do with constructing multiple models. Instead, Greene has suggested that participants may find the conclusions from valid, multiple-model categorical syllogisms awkward to express because they have the form Some A are not B, a form not frequently used in everyday language.

According to Johnson-Laird and Byrne (1991), however, errors in reasoning have three main sources: First, reasoning errors can occur when people fail to verify that the conclusion drawn from an initial model is valid; that is, people fail to search alternative models. Second, reasoning errors can occur when people prematurely end their search for alternative models because of working memory limitations. Third, reasoning errors can occur when people construct an inaccurate initial model of the task information. In this latter case, the error is not so much a reasoning error as it is an encoding error.

Recent research suggests that people may not search for alternative models spontaneously (Evans et al., 1999). In one study in which participants were asked to endorse conclusions that followed only necessarily from sets of categorical premises, Evans et al. (1999) found that participants endorsed conclusions that followed necessarily from the premises as frequently as conclusions that followed possibly but strongly from the premises (means of 80 and 79%, respectively). Evans et al. (1999) defined possible strong conclusions as conclusions that are unnecessary given their premises but that are regularly endorsed as necessary. Assuming that participants had taken seriously the instruction to endorse only necessary conclusions, Evans et al. (1999) had expected participants to endorse the necessary conclusions more frequently than the possible strong conclusions. Unlike necessary conclusions, possible strong conclusions should be rejected after alternative models of the premises are considered. Participants, however, endorsed necessary and possible strong conclusions equally often. Evans et al. (1999) explained the equivalent endorsement rates by suggesting that participants were not searching for alternative models of the premises but, instead, were using an initial model of the premises to evaluate both necessary and possible strong conclusions. Evans et al. (1999) suggested that if participants were constructing a single model of the premises, then possible strong conclusions should be endorsed as frequently as necessary conclusions because, in both cases, an initial model of the premises would support the conclusion. Participants, however, did not frequently endorse conclusions that followed possibly but weakly from the categorical premises (mean of 19%), that is, conclusions that are unnecessary given their premises and that are rarely endorsed as necessary. In this case, according to Evans et al. (1999), an initial model of the premises would not likely support the conclusion. Evans et al. concluded from this study that although previous research has shown that people can search for alternative models in some circumstances (e.g., the Newstead and Evans, 1993, study indicated that participants were highly motivated to search for alternative models of unbelievable conclusions from categorical syllogisms), people do not necessarily employ such a search in all circumstances.

Although mental model theory has been used successfully to account for a number of different results (for a review see Schaeken, DeVooght, Vandierendonck, & d’Ydewalle, 2000), it has been criticized for not detailing clearly how the process of model construction is achieved (O’Brien, 1993). For instance, it might be useful if the process of model construction was mapped onto a series of stages of information processing, such as the stages—encoding, combination, comparison, and response—outlined in Guyote and Sternberg (1981; Sternberg, 1983). In addition, the theory is unclear as to whether models serve primarily as strategies or whether models should be considered more basic components of the mind’s cognitive architecture.

Oedipus might have employed mental models to solve the sphinx’s riddle. For example, Oedipus could have constructed the following models of the riddle:

X = a, b b b b

X = a, b b

X = a, b b b

X = ?

Where X represents the same something or someone over time, a represents voice, and b represents feet.

In the models above, X is the unknown entity whose identity needs to be deduced. Each line of the display above reflects a different model or state of time. For example, X = a, b b b b is the first model of the unknown entity at infancy when it has one voice and four feet (crawls on all fours). An examination of the models above, however, does not suggest what conclusion can be deduced. The answer to the riddle is far from clear. The models might be supplemented with additional information, but what other information might be incorporated? Failing to deduce a conclusion from the models above, Oedipus could have decided to construct additional models of the information presented in the riddle. But how would Oedipus go about selecting the additional information needed to construct additional models? This is the same problem that was encountered in our discussion of syntactic rule theory: When one is reasoning about uncertain problems, additional information is a prerequisite to solving the problems, but how this additional information is selected from the massive supply of information stored in memory is left unspecified. It is not an easy problem, but it is one that makes the theory of mental models as difficult to use as syntactic rule theory in explaining Oedipus’s response, even though the theories are general ones that, in principle, can be applied to any task, regardless of content.

Verbal Comprehension Theory

This theory is similar to the theory of mental models in the initial inference steps a reasoner is expected to follow in interpreting a reasoning task (i.e., constructing an initial model of the premises and attempting to deduce a conclusion from the initial model). Unlike the theory of mental models, however, verbal comprehension theory does not propose that people search for alternative models of task information.

Polk and Newell (1995), the originators of verbal comprehension theory, have proposed that people draw conclusions automatically from information as part of their everyday efforts at communication. In deductive reasoning tasks, however, when a conclusion is not immediately obvious, Polk and Newell have suggested that people attempt to interpret the task information differently until they are able to draw the proper conclusion. Interpretation and reinterpretation define reasoning, according to verbal comprehension theory, and not the search for alternative models, as in mental model theory. In spite of this alleged dissimilarity between verbal comprehension theory and mental model theory, it is not entirely clear how the iterative interpretation process differs from the search for models.

Polk and Newell (1995) have suggested that people commit errors on deductive tasks because “linguistic processes cannot be adapted to a deductive reasoning task instantaneously” (p. 534). That is, reasoning errors occur because people’s comprehension processes are adapted to everyday situations and tasks and not to deductive tasks that require specific and formal interpretations.

Polk and Newell (1995) have presented a computational model of categorical syllogistic reasoning based on verbal comprehension theory that accounts for some standard findings in the psychological literature. The computational model, VR, produces regularities commonly and robustly observed in human studies of syllogistic reasoning. For example, whereas people, on average, answer correctly 53% of categorical syllogism problems, VR generates correct answers to an average of 59% of such problems. Also, whereas people, on average, construct valid conclusions that match the atmosphere or surface similarities of the premises on 77% of categorical syllogism problems, VR generates similar conclusions on 93% of the problems.

Verbal comprehension theory can only be used to account for reasoning on tasks that supply the reasoner with all the information he or she will need to reach a conclusion (Polk & Newell, 1995). For this reason, this theory cannot be used to explain how Oedipus might have solved the sphinx’s riddle, unless we can find out what additional information Oedipus used to solve the riddle. If we assume that Oedipus supplied additional information, then how did Oedipus select the additional information? This is the same question we asked when considering syntactic rule theory and mental model theory. The sphinx’s riddle, as with so many of the problems people face in everyday situations, requires the consideration of information beyond that presented in the problem statement. Any theory that fails to outline how this search for additional information occurs is hampered in its applicability to everyday reasoning.

Verbal comprehension theory has additional limitations. One criticism of the theory is that it fails to incorporate findings that show the use of nonverbal methods of reasoning, such as spatial representations, to solve categorical and linear syllogisms (Evans, 1989; Evans, Newstead, et al., 1993; Ford, 1995; Galotti, 1989; Sternberg, 1980a, 1980b, 1981). For example, Ford (1995) found that some individuals used primarily verbal methods to solve categorical syllogisms, whereas other individuals used primarily spatial methods to solve categorical syllogisms. Individuals employing spatial methods constructed a variant of Euler circles to evaluate conclusions derived from categorical syllogisms. Moreover, in studies of linear syllogisms (i.e., logical tasks about relations between entities), researchers reported that participants created visual, mental arrays of both the items and the relations in the linear syllogisms in the process of evaluating conclusions (for a review see Evans, Newstead, et al., 1993). Verbal comprehension theory is also ambiguous as to whether verbal comprehension operates at the level of strategies or at the level of cognitive architecture. Polk and Newell (1995) described verbal reasoning as a strategy that involves the linguistic processes of encoding and reencoding, but some linguistic processes are more automatic than controlled (see Evans, 2000). If verbal reasoning is to be viewed as a strategy, then future treatments of the theory might need to identify the specific linguistic processes that are controlled by the reasoner and how this control is achieved.

Evolutionary Theories

According to evolutionary theories, domain-specific reasoning mechanisms have evolved to help human beings meet specific environmental needs (Cosmides & Tooby, 1996).

Social Contract Theory

Unlike most of the previous theories discussed that advance domain-general methods of reasoning, social contract theory advances domain-specific algorithms for reasoning (Cosmides, 1989). These Darwinian algorithms are hypothesized to focus attention, organize perception and memory, and invoke specialized procedural knowledge for the purpose of making inferences, judgments, and choices that are appropriate for a given domain. According to Cosmides (1989), one domain that has cultivated a specialized reasoning algorithm involves situations in which individuals must exchange services or objects contingent on a contract. It is hypothesized that when individuals reason in a social-exchange domain, a social-contract algorithm is invoked.

The social-contract algorithm is an example of a Darwinian algorithm that allegedly developed out of an evolutionary necessity for “adaptive cooperation between two or more individuals for mutual benefit” (Cosmides, 1989, p. 193). The algorithm is induced in situations that reflect a cost-benefit theme and involve potential cheaters— individuals who might take a benefit without paying a cost. The algorithm includes a look-for-cheaters procedure that focuses attention on anyone who has not paid a cost but might have taken a benefit.

Social contract theory was initially proposed as a rival to Cheng and Holyoak’s (1985) pragmatic reasoning theory.The two theories are very similar, leading some investigators to view social contract theory as simply a more specific versionof pragmatic reasoning theory: a version that focuses on contracts specifically instead of obligations and permissions generally (Pollard, 1990). Cosmides’s (1989) social contract theory has been used to account for participants’ poor performance on abstract versions of the selection task. According to the theory, reasoning errors occur whenever the context of a reasoning task fails to induce the social-contract algorithm. Cosmides has claimed that the social-contract algorithm is induced in concrete, thematic versions of the Wason selection task and that this is the reason for participants’improved performance on thematic versions of the task. Figure 23.2 illustrates a social-contract representation of theWason selection task.

Many of the same weaknesses identified in pragmatic reasoning theory can also be identified in social contract theory. First, social contract theory lacks generality because it was developed primarily to explain performance on thematic versions of the selection task. Second, the status of the socialcontract algorithm is unclear. On the one hand, the algorithm is described as a strategy that is induced in cost-benefit contexts, but it is unclear whether participants select this strategy or whether the strategy is induced automatically. If it is induced automatically, then its status as a strategy is questionable because strategies are normally under an individual’s control (Evans, 2000). If it is not induced automatically, then one needs to inquire how it is selected from among all available algorithms. On the other hand, the algorithm’s proposed evolutionary origin would suggest that it might be a fundamental mechanism used to represent specific kinds of contextual information. In other words, if an algorithm has evolved over time to facilitate reasoning in particular contexts (e.g., social-exchange situations), then one would expect most, if not all, human beings to have the algorithm as part of their cognitive architecture. One would not expect such a basic algorithm to have the status of a strategy.

Cheating Detection Theory

Cheating detection theory (Gigerenzer & Hug, 1992) is similar to social contract theory. However, unlike social contract theory, it explores how a reasoner’s perspective influences reasoning performance. Gigerenzer and Hug (1992) have maintained the view that individuals possess a reasoning algorithm for handling social contracts. However, unlike Cosmides (1989), they have proposed that the algorithm yields different responses, depending on the perspective of the reasoner; that is, the algorithm leads participants to generate different responses depending on whether the participant is the recipient of the benefit or the bearer of the cost. For instance, in the following conditional permission rule originally used by Manktelow and Over (1991) in a thematic version of the selection task (see also Manktelow, Fairley, Kilpatrick, & Over, 2000), the perspective of the reasoner determines who and what defines cheating and, therefore, what constitutes potentially violating evidence:

If you tidy your room, then you may go out to play.

This rule, which was uttered by a mother to her son, was presented to participants along with four cards. Each card had a record on one side of whether the boy had tidied his room and, on the other, whether the boy had gone out to play, as follows: room tidied (P), room not tidied (not-P), went out to play (Q), or did not go out to play (not-Q). Participants were then asked to detect possible violations of the rule either from the mother’s perspective or from the son’s perspective. Participants who were asked to assume the son’s perspective selected the room tidied (P) and did not go out to play (not-Q) cards most frequently as instances of possible violations of the rule. These instances correspond to the correct solution sanctioned by standard logic. Participants who were asked to assume the mother’s perspective, however, selected the room not tidied (not-P) and went out to play (Q) cards most frequently as instances of possible violations—the mirror image of the standard correct solution. From these responses, it seems that participants are sensitive to perspective in reasoning tasks (e.g., Gigerenzer & Hug, 1992; Light, Girotto, & Legrenzi, 1990).

As is the case with social contract theory, cheating detection theory grew out of an attempt to understand performance on thematic versions of the selection task. As with social contract theory, facilitated performance on the selection task is believed to be contingent on the task’s context. If the context of the task induces the cheating-detection algorithm, then performance is facilitated, but if the context of the task fails to induce the algorithm, then performance suffers. Thus, cheating detection theory can be criticized for having the same weaknesses as social contract theory; in particular, its scope is too narrow to account for reasoning in general.

Heuristic Theories

A heuristic is a rule of thumb that often but not always leads to a correct answer (Fischhoff, 1999; Simon, 1999a). Some researchers (e.g., Chater & Oaksford, 1999) have proposed that heuristics are used instead of syntactic rules or mental models to reason in everyday situations. Because everyday inferences are often uncertain and can be easily overturned with knowledge of additional information (i.e., everyday inferences are defeasible in this sense), some investigators have proposed that heuristics are well adapted for reasoning in everyday situations (e.g., Holland, Holyoak, Nisbett, & Thagard, 1986). Chater and Oaksford (1999) have illustrated the uncertainty of everyday inferences with the following example: Knowing Tweety is a bird and Birds fly makes it possible to infer that Tweety can fly, but this conclusion is uncertain or can be overturned upon learning that Tweety is an ostrich. According to Chater and Oaksford (1999), defeasible inferences are problematic for syntactic rule theory and mental model theory because these theories offer mechanisms for how inferences are generated but not for how inferences are overturned, if at all. Consequently, other approaches need to be considered to explain how individuals draw defeasible inferences under everyday conditions.

Judgment Under Uncertainty

Tversky and Kahneman (1974, 1986) outlined several heuristics for making judgments under uncertainty. For example, one of the heuristics they discovered is displayed when people are asked to answer questions such as What is the probability that John is an engineer? According to Tversky and Kahneman (1974), many people answer such a question by evaluating the degree to which John resembles or is representative of the constellation of traits associated with being an engineer. If participants consider that John shares many of the traits associated with being an engineer, then the probability that he is an engineer is judged to be high. Evaluating the degree to which A is representative of B in order to answer questions about the probability that Aoriginated with or belongs to B might often lead to correct answers, but it can also lead to systematic errors. In order to improve the likelihood of generating accurate answers, Tversky and Kahneman (1974) suggested that participants consider the base rate of B (e.g., the probability of being an engineer in the general population) before determining the probability that Abelongs to B.

Another heuristic that is used to make judgments under uncertainty can be observed when people are asked to assess the probability of an event, for example, the probability that it will rain tomorrow. In this case, many people might assess the probability that it will rain by the ease with which they generate or make available thoughts of last week’s rainy days. This heuristic can lead to errors if people cannot generate any instances of rain or if people employ a biased search, in which they ignore all of last week’s sunny days and focus only on the rainy days in assessing the probability of rain tomorrow. Tversky and Kahneman (1974, 1986) considered that people’s reliance on heuristics undermined the view of people as rational and intuitive statisticians. Other investigators disagree.

Fast and Frugal Heuristics

Gigerenzer, Todd, and their colleagues from the ABC research group (1999) have suggested that people employ fast and frugal heuristics that take a minimum amount of time, knowledge, and computation to implement, and yield outcomes that are as accurate as outcomes derived from normative statistical strategies. Gigerenzer et al. (1999) have proposed that people use these simple heuristics to generate inferences in everyday environments. One such heuristic exploits the efficiency of recognition to draw inferences about unknown aspects of the environment. In a description of the recognition heuristic, Gigerenzer et al. stated that in tasks in which one must choose between two alternatives and only one is recognized, the recognized alternative is chosen. As this statement suggests, the recognition heuristic can be applied only when one alternative is less recognizable than the other alternative.

In a series of experiments, Gigerenzer et al. (1999) showed that people use the recognition heuristic when reasoning about everyday topics. For example, in one experiment, 21 participants were shown pairs of American cities plus additional information about each of the cities and asked to choose the larger city of each pair. The results showed that participants’ choices of large cities tended to match those cities they had selected in a previous study as being more recognizable. The recognition heuristic can often lead to accurate inferences because objects or places that score very high (or very low) on a particular criterion are normally made salient in our environment; their atypical characteristics make them stand out.

The recognition heuristic also yields accurate inferences in business situations such as those that involve stock market transactions. In one study, 480 participants were grouped into one of four categories of stock market expertise—American laypeople,American experts, German laypeople, and German experts—and asked to complete a company recognition task of American and German companies (Gigerenzer et al., 1999). Participants then monitored the progress of two investment portfolios, one consisting of companies they recognized highly in the United States and the other consisting of companies they recognized highly in Germany. Participants analyzed the performance of the investment portfolios for a period of 6 months. Results showed that the recognition knowledge of laypeople turned out to be only slightly less profitable than the recognition knowledge of experts. For instance, the investment portfolio of German stocks based on the recognition of the German experts gained 57% during the study; however, German stocks based on the recognition of the German laypeople gained 47% during the same period— only 10% less than the gains made by means of expert advice! The investment portfolios of U.S. stocks based on the recognition of American laypeople and experts did not make such dramatic gains (13 vs. 16%, respectively). However, in all cases, portfolios consisting of recognized stocks yielded average returns that were 3 times as high as the returns from portfolios consisting of unrecognized stocks. These findings indicate that when one is investing, a simple heuristic might be a worthwhile strategy.

Probability Heuristic Model

Another heuristic approach to reasoning is Chater and Oaksford’s (1999) probability heuristic model (PH model) of syllogistic reasoning (see also Oaksford & Chater, 1994). According to Chater and Oaksford, simple heuristics can account for many of the findings in syllogistic reasoning studies without the need to posit complicated search processes. In the PH model, quantified statements such as All birds are small or Most apples are red are ordered based on their informational value. Using convex regions of a similarity space to model informativeness, Chater and Oaksford showed mathematically that different quantified statements vary in how much space they occupy in the similarity space. Categories such as all and most in quantified statements occupy a small proportion of the similarity space and overlap greatly, and are thus considered more informative than those quantified statements whose categories occupy a larger proportion of the similarity space and do not overlap greatly (see their Appendix A, p. 242). In other words, quantified statements considered to be high in informational value are those “that surprise us the most if they turn out to be true” (Chater & Oaksford, 1999, p. 197) because we perceive them as unlikely. In Chater and Oaksford’s (1999) computational analysis, quantifiers are ordered as follows:

All > Most > Few > Some . . . are > No . . . are >>

Some . . . are not

where > stands for more informative than.

Thus, statements containing the quantifier all, such as All people are tall, are considered more informative than statements containing the quantifier most, such as Most people are tall.

One informational strategy based on this ordering is the min-heuristic, which involves choosing a conclusion to a premise set that has the same quantifier as that of the least informativepremise(themin-premise).Thus,ifthefirstpremise contains the quantifier all and the second premise contains the quantifier some, the min-heuristic would suggest selecting some as the quantifier for the conclusion as follows:

All Y are X

Some Z are Y (min-premise)

Some X are Z

Chater and Oaksford (1999) showed that the min-heuristic could be used to predict the conclusions participants generated to valid categorical syllogisms with almost perfect accuracy. The min-heuristic predicted correctly conclusions of the form All A are B, No A are B, and Some A are B but failed slightly to predict conclusions of the form Some A are not B (see their Appendix C, p. 247). The min-heuristic also accounted for the conclusions participants generated incorrectly to invalid syllogisms.

Chater and Oaksford’s (1999) PH model fares well against other accounts of syllogistic reasoning. For example, when the PH model was used to model Rips’s (1994) syllogistic reasoning results, it obtained as good a fit as Rips’s model but with fewer parameters. Moreover, Chater and Oaksford showed that the PH model predicts the differences in difficulty between single-model syllogisms and multiple-model syllogisms described in mental model theory. According to the PH model, participants might be more inclined to solve single-model syllogisms correctly because they lead to more informative conclusions than those arising from multiplemodel syllogisms.

Although the heuristics described in Chater and Oaksford’s (1999) PH model account for many of participants’ responses to categorical syllogisms, the application of their model to other reasoning tasks is unclear. It is unclear how their heuristics can be extended to everyday reasoning tasks in which people must generate conclusions from incomplete and often imprecise information. In addition, these heuristics need to be embedded in a wider theory of human reasoning.

Theorists who promote the fast and frugal heuristic approach to reasoning maintain that heuristics are adaptive responses to an uncertain environment (Anderson, 1983; Chater & Oaksford, 1999; Gigerenzer et al., 1999). In other words, heuristics should not be viewed as irrational responses (even when they do not generate standard logical responses) but as reflections of the way in which human behavior has come to be adaptive to its environment (see also Sternberg & Ben Zeev, 2001). Although the heuristic approach reminds us of the efficiency of rules of thumb in reasoning, it does not explain how people reason when fast and simple heuristics are eschewed. For example, what are the strategies that reasoners invoke when they have decided they want to expend the time and effort to search for the best alternative? It is hard to imagine that heuristics characterize all human reasoning, because factors such as context, instructions, effort, and interest might cue more elaborate reasoning processes.

Factors that Mediate Reasoning Performance

Context

Context can facilitate or hinder reasoning performance. For example, if the context of a reasoning task is completely meaningless to a reasoner, then it is unlikely that the reasoner will be able to use previous experiences or background knowledge to generate a correct solution to the task. It might be possible for a reasoner to generate a logical conclusion to a nonsensical syllogism if the reasoner is familiar with logical necessity but not if he or she is unfamiliar with logical necessity. If a task fails to elicit any background knowledge, logical or otherwise, it is difficult to imagine how someone might establish a sensible starting point in his or her reasoning. For instance, some critics of the abstract version of the Wason selection task have argued that participants perform poorly on the task because the task’s abstract context fails to induce a domain-specific reasoning algorithm (e.g., Cheng & Holyoak, 1985, 1989; Cosmides, 1989).

That participants’ reasoning performance improves on thematic (or concrete) versions of the selection task, however, does not demonstrate participants’ understanding of logic. Recall that depending on the perspective the reasoner assumes, a reasoner will choose the not-P and Q cards as easily as the P and not-Q cards in the selection task (see the section titled “Cheating Detection Theory”; Gigerenzer & Hug, 1992; Manktelow & Over, 1991; Manktelow et al., 2000). The facility with which reasoners can change their card choices depending on the perspective they assume suggests that logical principles are not guiding their performance, but, rather, the specific details of the situation. It appears that contextual factors, outside of logic, have a significant influence upon participants’ reasoning.

Instructions

The instructions participants receive prior to a reasoning task have been shown to influence their performance. For instance, instructing participants about the importance of searching for alternative models has been shown to improve their performance on categorical syllogisms (Newstead & Evans, 1993). Additionally, in thematic versions of the selection task, Pollard and Evans (1987) found that instructing participants to enforce a rule led to better performance than did instructing them to test a rule.

Rule enforcement is what Cheng and Holyoak (1985) and Cosmides (1989) asked participants to do in their studies of thematic versions of the selection task. Cheng and Holyoak asked participants to enforce the rule—If the form says ENTERING on one side, then the other side includes cholera among the list of diseases—by selecting those cards that represented possible violations of the rule. In contrast, traditional instructions to the selection task have involved asking participants to select cards that will test the truth or falsity of the conditional rule. Liberman and Klar (1996) have claimed that asking participants to enforce a rule, by searching for violating instances, is not the same as asking participants to test a rule, by searching for falsifying instances; the latter task is more difficult than the former task because participants must reason about a rule instead of from a rule.

Reasoning about a rule is considered to be a more difficult task than reasoning from a rule. Reasoning about a rule requires the metacognitive awareness underlying the hypothetico-deductive method of hypothesis testing; that is, participants reasoning about a rule must test the epistemic status or reliability of the rule (Liberman & Klar, 1996). In contrast, participants reasoning from a rule do not test the reliability of the rule but, instead, assume the veracity of the rule and then check for violating instances. Critics of thematic versions of the selection task have argued that enforcer instructions induce participants to think of counterexamples to the rule without understanding the logical structure of the task (Wason, 1983).

The existence of perspective effects provides some evidence that enforcer instructions change the demands of the selection task from that of logical rule testing to that of simple rule following. The perspective of the participant is a contextual variable that leaves the logical structure of the task unchanged. Thus, if participants are aware of the task’s underlying logical structure, then their perspective of the task should not influence their choice of cards—the P and not-Q remain the correct card choices regardless of perspective. However, recall that asking participants to assume different perspectives in a thematic version of the selection task influenced their choice of cards. Sometimes participants chose the P and not-Q cards as violating instances of the conditional rule, and sometimes they chose the not-P and Q cards as violating instances of the conditional rule (see the section titled “Cheating Detection Theory”; Gigerenzer & Hug, 1992). The ease with which participants altered their card choices suggests that their reasoning was influenced more by contextual variables than by logic. The improved performance obtained with the use of enforcer instructions has led some investigators to doubt that these results should be compared with results obtained using traditional instructions (e.g., Griggs, 1983; Liberman & Klar, 1996; Manktelow & Over, 1991; Noveck & O’Brien, 1996; Rips, 1994; Wason, 1983).

Although enforcer instructions might alter the purpose of the abstract selection task, the results obtained with these instructions are significant. That participants manifest a semblance of logical reasoning with enforcer instructions seems to point to the specificity of competent reasoning. This specificity does not refer to the specific brain modules that, according to some researchers, have evolved to help people reason in particular domains (e.g., Cosmides, 1989; Cosmides & Tooby, 1996). Rather, this specificity might be more indicative of the specific background knowledge needed to reason competently (e.g., Chi, Glaser, & Farr, 1988). One reason that enforcer instructions might facilitate reasoning on thematic versions of the selection task is that they cue very specific knowledge about rule enforcement. Most people learn extensively about rule enforcement from an early age. Enforcer instructions might induce the use of specific knowledge about rule enforcement. In short, enforcer instructions might facilitate reasoning performance by permitting participants to use their background knowledge.

Relevance

It is reasonable to assume that individuals will be motivated to solve tasks that are relevant to their lives. The sphinx’s riddle must have had immediate relevance for the men who tried to answer it; indeed, the riddle provoked a situation that constituted a life-or-death affair. Sperber, Cara, and Girotto (1995) have proposed that people gauge the relevance of a task to themselves by determining its cognitive effect (i.e., the benefits of the task) and its processing effort (i.e., the costs of performing the task). According to Sperber et al., a relevant task is one that requires minimal processing effort or whose solution is beneficial, or both. For instance, a task that requires significant processing effort might be considered relevant if its benefits are great (e.g., going to college).

Assessments of task relevance are related to an individual’s knowledge, however. For example, being knowledgeable about a task might reduce the reasoner’s perception of the processing efforts required to solve it. Conversely, a task that promises great rewards might inspire the reasoner to become knowledgeable about the task’s contextual domain. According to Cosmides (1989), for example, the promise of benefits (and the fear of loss) inspired a social-contract algorithm to evolve to help human beings negotiate goods in social-exchange situations. Sperber et al. (1995) have claimed that tasks in any conceptual domain can achieve relevance.

Reasoners who can solve tasks within a contextual domain with little processing effort and who view these tasks as beneficial are likely to be those who have some domain-specific knowledge about the tasks. Because a person’s domainspecific knowledge seems to be closely linked to how task relevance is assessed and, therefore, to the person’s motivation for solving the task, domain-specific knowledge appears fundamental to performance on reasoning tasks. If knowledge is fundamental to reasoning, then how did Oedipus solve the sphinx’s riddle? He had little domain-specific knowledge about the riddle. Perhaps Oedipus did not resolve the riddle by reasoning after all. Perhaps he resolved it by problem solving.

Problem Solving

Problem solving is defined as the goal-driven process of overcoming obstacles that obstruct the path to a solution (Simon, 1999a; Sternberg, 1999). Problem solving and reasoning are alike in many ways. For example, in both problem solving and reasoning, the individual is creating new knowledge, albeit in the form of a solution needed to reach a goal or in the form of a conclusion derived from evidence, respectively. Problem solving and reasoning seem to differ, however, in the processes by which this new knowledge is created. In problem solving, individuals use strategies to overcome obstacles in pursuit of a solution (Newell & Simon, 1972). In reasoning, however, the role of strategies is not as clear. It was mentioned earlier that reasoning theories, such as syntactic rule theory, pragmatic reasoning theory, and mental model theory, do not explicitly specify if syntactic rules, pragmatic reasoning schemas, and mental models, respectively, should be viewed as strategies or, more fundamentally, as forms of representing knowledge. Representation refers to the way in which knowledge or information is formalized in the mind, whereas strategy refers to the methods by which this knowledge or information is manipulated to reach a goal. Although individuals may be consciously aware of the strategies they choose to solve problems, individuals are believed to be unaware of how they represent knowledge, which is considered to be part of the mind’s cognitive architecture.

It is possible that strategies are unimportant in reasoning because the objective in reasoning is not to reach a goal so much as it is to infer what follows from evidence; the conclusion is meant perhaps to fall out of the set of premises without too much work on the part of the reasoner. Although some reasoning tasks do require goal-oriented conclusions that are not easily deduced—or directly deduced at all—from the premises, it might be more accurate to describe such reasoning tasks as more akin to problem-solving tasks (Galotti, 1989; Evans, Over, & Manktelow, 1993). For instance, reasoning tasks leading to inductive inferences—inferences that go beyond the information given in the task—might be considered more akin to problem-solving tasks. Strategies, however, are clearly important in problem solving because the goal in problem solving is to reach a solution, which is not always derived deductively or even solely from the problem information.

Knowledge Representation and Strategies in Problem Solving

Production Systems

The distinction between representation and strategy is made explicit in the problem-solving literature. For example, some investigators propose that knowledge is represented in terms of production systems (Dawson, 1998; Simon, 1999b; Sternberg, 1999). In a production system, instructions (called productions) for behavior take the following form:

IF<<conditions> , THEN<<actions>.

The form above indicates that if certain conditions are met or satisfied, then certain actions can be carried out (Simon, 1999b). The conditions of a production involve propositions that “state properties of, or relations among, the components of the system being modeled” (Simon, 1999b, p. 676). A production system is normally implemented following a match between the conditions of the production and elements stored in working memory. The production is implemented when the conditions specified in the production’s IF clause are satisfied or met by the elements of working memory. Following the satisfaction of the production system’s IF clause with the elements of working memory, an action is initiated (as specified in the production system). The action may take the form of a motor action or a mental action such as the elimination or creation of working memory elements (Simon, 1999b).

The elements of working memory may satisfy the conditions of numerous productions at any given time. One way in which all the productions that are executable at a given moment can be restrained from overwhelming the problem solver is through the presence of goals. Agoal can be defined simply as a symbol or representation that must be present both in the conditions of the production and in working memory before that production is activated. In other words, a goal provides a more stringent condition that must be met by an element in working memory before the production is activated (Simon, 1999b). In the following example of a production system, the goal is to determine if a particular sense of the word knows is to be applied (taken from Lehman, Lewis, & Newell, 1998, p. 156):

IF comprehending knows, and

     there’s a preceding word, and

     that word can receive the subject role, and

     the word refers to a person, and the word is third person singular,

THEN use sense 1 of knows.

The antecedent or the condition of the production consists of a statement of the goal (i.e., comprehending knows), along with additional conditions that need to be met before the consequent or action is applied (i.e., use sense 1 of knows). Although the above production system might look like a strategy, it is not because knowledge has not been manipulated.

Parallel Distributed Processing (PDP) Systems

Other theories of knowledge representation exist outside of production systems. For example, some investigators propose that knowledge is represented in the form of a parallel distributed processing (PDP) system (Bechtel & Abrahamsen, 1991; Dawson, 1998; Dawson, Medler, & Berkeley, 1997). A PDP system involves a network of inter-connected, processing units that learn to classify patterns by attending to their specific features. A PDP system is made up of simple processing units that communicate information about patterns by means of weighted connections. The weighted connections inform the recipient processing unit whether a to-beclassified pattern includes a feature that the recipient processing unit needs to attend to and use in classifying the pattern. According to PDP theory, knowledge is represented in the layout of connections that develops as the system learns to classify a set of patterns. In Figure 23.3, a PDP representation of the Wason (1966) selection task is shown. This representation illustrates a network that has learned to select the P and Q in response to the selection task (Leighton & Dawson, 2001). The conditional rule and set of four cards are coded as 1s and 0s and are presented to the network’s input unit layer. The network responds to the task by turning on one of the four units in its output unit layer, which correspond to the set of four cards coded in the input unit layer. The layer of hidden units indicates the number of cuts or divisions in the pattern space required to solve the task correctly (i.e., generate the correct responses to the task). Training the network to generate the P response required a minimum of three hidden units.

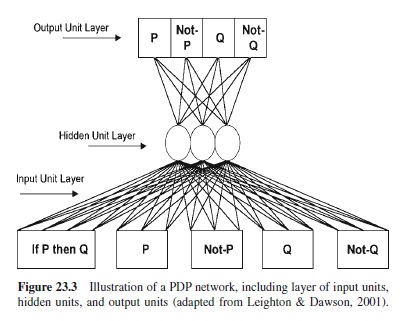
Strategies can be extracted from a PDP system. The process by which strategies are identified in a PDP system is laborious, however, and requires the investigator to examine the specific procedures used by the system to classify a set of patterns (Dawson, 1998).

Algorithms

The representation of knowledge provides the language in which cognitive processes in models of cognitive systems can be described. An algorithm is one cognitive process for accomplishing an explicit outcome. More specifically, an algorithm is made up of a finite set of operations that is straightforward and unambiguous and, when applied to a set of objects (e.g., playing cards, chess pieces, computer parts), leads to a specified outcome (Dietrich, 1999). The initial state of the set of objects constitutes the input to the algorithm, and the final state of the objects constitutes the output of the algorithm. The initial state of objects is transformed into a final state by implementing the operations of the algorithm that correspond to state transitions. Algorithms can be described more specifically when the context of the algorithm is defined because an algorithm’s clarity and simplicity are relative to the context in which it is being applied (Dietrich, 1999). An example of an algorithm might be the instructions included with a new desktop computer (at least, such instructions are supposed to be algorithms). If one follows the instructions for installing all the parts of the computer, the outcome is certain: a working computer. Algorithms are sometimes unavailable for accomplishing certain outcomes; under these circumstances, heuristics can be implemented to approximate the desired outcome.

Heuristics

A problem-solving heuristic is a rule of thumb for approximating a desired outcome. As with reasoning heuristics, problem-solving heuristics sometimes produce desired outcomes and sometimes not. Heuristics are imperfect strategies (Fischhoff, 1999). Examples of heuristics are considered below in the context of Newell and Simon’s model of problem solving.

Theories of Problem Solving

Newell and Simon’s Model of Problem Solving

Even after 25 years, Newell and Simon’s (1972) model of problem solving remains influential today. Newell and Simon’s model of problem solving was generated from computer simulations and from participants’ think-aloud responses as they worked through problems. According to the model, the problem solver perceives both the initial state, the state at which he or she originally is, and the goal state, the state that the problem solver would like to achieve. Both of these states occupy positions within a problem space, the universe of all possible actions that can be applied to the problem, given any constraints that apply to the solution of the problem (Simon, 1999a; Sternberg, 1999).

In the ongoing process of problem solving, a person decomposes a problem into a series of intermediate steps with the purpose of bringing the initial state of the problem closer to the goal state. At each intermediate step prior to the goal state, the subgoal is to achieve the next intermediate step that will bring the problem solver closer to the goal state. Each step toward the goal state involves applying an operation or rule that will change one state into another state. The set of operations is organized into a program, including sublevel programs. The program can be a heuristic or an algorithm, depending on its specific nature. In short, according to Newell and Simon’s (1972) model, problem solving is a search through a series of states within a problem space; the solution to a problem lies in finding the correct sequence of actions for moving from one (initial) state to another (goal) state (Newell & Simon, 1972; Simon, 1999a; Sternberg, 1999).

A variety of heuristics can be used for changing one state into another. For example, the difference-reduction method involves reducing the difference between the initial state and goal state by applying operators that increase the surface similarity of both states. If an operator cannot be directly applied to reduce the difference between the initial state and goal state, then the heuristic is discarded.Another method that is similar to the difference-reduction method is Newell and Simon’s (1972) means-ends analysis, a heuristic Newell and Simon studied extensively in a computer simulation program (i.e., General Problem Solver [GPS]) that modeled human problem solving. Means-end analysis is similar to the difference-reduction method, with the exception that if an operator cannot be directly applied to reduce a difference between the initial state and goal state, then, instead of the strategy’s being discarded, a sub-goal is set up to make the operator applicable (Simon, 1999a).

Analogy is another heuristic. Under this heuristic, the problem solver uses the structure of the solution to an analogous problem to guide his or her solution to a current problem. The main focus in research on analogy is in how people interpret or understand one situation in terms of another; that is, how it is that one situation is mapped onto another for problemsolving purposes (Gentner, 1999). Two main subprocesses are proposed to mediate the use of analogy. According to Gentner’s structure-mapping theory (1983), an unfamiliar situation can be understood in terms of another familiar situation by aligning the representational structures of the two situations and projecting inferences from the familiar case to the unfamiliar case. The alignment must be structurally consistent such that there is a one-to-one correspondence between the mapped elements in the familiar and unfamiliar situations. Inferences are then projected from the familiar to the unfamiliar situation so as to obtain structural completion (Gentner, 1983, 1999). Following this alignment, the analogy and its inferences are evaluated by assessing (a) the structural soundness of the alignment between the two situations; (b) the factual validity of the inferences, because the use of analogy does not guarantee deductive validity; and (c) whether the inferences meet the requirements of the goal that prompted the use of the analogy in the first place (Gentner, 1999).

Recent research suggests that use of analogy in real-world contexts is based on structural or deep underlying similarities, instead of surface or superficial similarities, between the unfamiliar situation and the familiar situation (Dunbar, 1995, 1997). For example, Dunbar (1997) found that over 50% of analogies that scientists generated at weekly meetings in a molecular biology lab were based on deep, structural features between problems, rather than on surface features between problems. In previous studies, however, investigators (e.g., Gentner, Rattermann, & Forbus, 1993) have found that participants in laboratory experiments sometimes rely on superficial features when using analogy. According to Blanchette and Dunbar (2000; see also Dunbar, 1995, 1997), participants’ reliance on superficial features when using analogy might be due to the kind of paradigm used to study analogy. For example, Blanchette and Dunbar indicated that previous studies have used a reception paradigm to study analogy use. Under the reception paradigm, participants are provided with both a target (less familiar) and a source (familiar) analog and then asked to indicate the relationships between both rather than being asked to generate their own source analogs. In a series of studies aimed at evaluating participants’ analogies, Blanchette and Dunbar found that when participants were given a target problem and asked to generate their own source analog, most of the analogies (67%) generated by participants did not exhibit superficial similarities with the target but, instead, exhibited deeper similarities with the target. The proportion of these deep analogies increased to 81% when participants worked individually. These results suggest that participants, like scientists, can generate analogies based on deep, structural features when laboratory conditions are more akin to real-world contexts, that is, when participants are free to generate their own source analogs.

Error is always a possibility when heuristics are used. Not only might a chosen heuristic be inappropriate for the problem under consideration, but a heuristic might be inappropriately used, resulting in unsuccessful problem solving. Heuristics such as the difference-reduction method, means-end analysis, analogy, and others (e.g., see Anderson, 1990, for further descriptions of the generate and test method, working forward method, and working backward method) are only general rules of thumb that work most of the time but not necessarily all of the time (Fischhoff, 1999; Holyoak, 1990; Simon, 1999a). They represent general problemsolving methods that can be applied with relative success to a wide range of problems across domains.

According to Newell and Simon (1972), the use of heuristics embodies problem solving because of the cognitive limitations or bounded rationality that characterizes human behavior (see also Sternberg & Ben Zeev, 2001). Simon (1991) described bounded rationality as involving two central components: the limitations of the human mind and the structure of the environment in which the mind must operate. The first of these components suggests that the human mind is subject to limitations, and, due to these limitations, models of human problem solving, decision making, and reasoning should be constructed around how the mind actually performs instead of on how the mind should perform from an engineering point of view. Foolproof strategies do not exist in everyday cognition because the ill-defined structure of our environment makes it unlikely that people can identify perfect heuristics for solving imperfect, uncertain problems. The second of these components suggests that the structure of the environment shapes the heuristics that will be most successfully applied in problem solving endeavors. If the environment is ill defined (in the sense that it reflects numerous uncertain tasks), then general heuristics that work most of the time and do not overburden the cognitive system will be favored (see also Brunswick, 1943; Gigerenzer et al., 1999; Shepard, 1990). Heuristics, however, are only one of the kinds of tools that facilitate problem solving. Investigators have also found that insight is an important variable that aids some forms of problem solving (Davidson & Sternberg, 1984; Metcalfe & Wiebe, 1987; Sternberg & Davidson, 1995).

Problem Solving by Means of Insight

Insightful problem solving can be defined as problem solving that is significantly assisted by the awareness of a key piece of information—information that is not necessarily obvious from the problem presented (Sternberg, 1999). It is believed that insight plays a role in the solution of ill-defined problems. Ill-defined problems are problems whose solution paths are elusive; the goal is not immediately certain. Because the solution path is elusive, ill-defined problems are challenging to represent within a problem space. Ill-defined problems are often termed insight problems because they require the problem solver to perceive the problem in a new way, a way that illuminates the goal state and the path that leads to a solution. Insight into a solution can manifest itself after the problem solver has put the problem aside for hours and then comes back to it. The new perspective one gains on a problem when coming back to it after having put it aside is known as an incubation effect (Dominowski & Jenrick, 1973; Smith & Blankenship, 1989).

Metcalfe and Wiebe (1987; see also Metcalfe, 1986, 1998) have shown that insightful problem solving seems to differ from ordinary (noninsightful) problem solving. For example, these investigators have shown that participants who are highly accurate in estimating their problem-solving success with ordinary problems are not as accurate in estimating their success with insight problems. The processes that might be responsible for these differences are not yet detailed, making this account more representative of a performance-based account than a process-based account of problem solving (for a fuller discussion of insight, see Sternberg & Davidson, 1995).

In a more process-oriented theory of insight, however, Davidson and Sternberg (1984) have offered a three process view of insight. These investigators have proposed that insightful problem solving manifests itself in three different forms: (a) Selective encoding insights involve attending to a part of the problem that is relevant to solving the problem, (b) selective comparison insights involve novel comparisons of information presented in the problem with information stored in long-term memory, and (c) selective combination insights involve new ways of integrating and synthesizing new and old information. Insight gained in any one of these three forms can facilitate insightful problem solving.

In addition, Knoblich, Ohlsson, Haider, and Rhenius (1999) have characterized insightful problem solving as overcoming impasses, states of mind in which the thinker is unsure of what to do next.These investigators have proposed that impasses are overcome by changing the problem representation by means of two hypothetical processes or mechanisms. The first mechanism involves relaxing the constraints imposed upon the solution, and the second mechanism involves decomposing the problem into perceptual chunks. In a series of four studies aimed at examining insightful problem solving, Knoblich et al. (1999) asked participants to solve insight problems called “match-stick arithmetic” problems. As shown in Figure 23.4, match-stick arithmetic problems involve false arithmetic statements written with Roman numerals (e.g.,I,II, IV), arithmetic operations (e.g., –, + ), and equal signs constructed out of matchsticks. The goal in matchstick problems is to move a single stick in such a way that the initial false arithmetic statement is transformed into a true statement. A move can be made on a numerical value or an operator and can consist of grasping a stick and moving it, rotating it, or sliding it.

According to Knoblich et al. (1999), matchstick problems can be solved by relaxing the constraints on how numerical values are represented, how operators are represented, and how arithmetic functions are supposed to be formed—for example, form of X = f(Y, Z). In particular, the numerical value constraint in arithmetic suggests that a numerical value on one side of an equation cannot be changed unless an equivalent change is made to the numerical value on the other side of the equation, such as when the same quantity is added to or subtracted from both sides of an equation. Relaxing the constraint on how numerical values are represented would involve accepting the possibility that a numerical value on one side of an equation can be changed without changing the other side of the equation as well (e.g., if 1 is subtracted from one side of the equation, this same operation need not be performed on the other side of the equation). Note that numerical value constraints do not include constraints on how the numerical quantities are perceived. For example, the numerical value constraint does not include constraints on whether the number 4 is perceived as IV or as IIII or some other representation. According to Knoblich et al. (1999), how numbers are perceived in the context of the matchstick task is better explained by considering the process of chunking.

Knoblich et al. (1999) suggest that decomposing elements of matchstick problems into perceptual chunks can also help to solve the problems. Perceptual decomposition involves, for instance, recognizing that the Roman numeral IV can be decomposed into the elements I and V, and that the resulting elements can be moved independently of each other to generate a true matchstick arithmetic equation. Roman numerals cannot, however, be decomposed into elements that are not used in constructing the numerals. For instance, the Roman numeral IV could not be decomposed into IIII because four vertical lines were not used to construct the numeral IV.

In an effort to examine how constraint relaxation and chunkingmediatedinsightfulproblemsolving,Knoblichetal. (1999) asked participants to solve matchstick problems of varying difficulty. After an initial training phase, participants were presented with two blocks of six matchstick problems on a computer screen and given 5 minutes to respond to each problem. Each block of problems contained instances of easy matchstick problems (i.e., Type A) and difficult matchstick problems (i.e., Type C and D). Results from their four studies revealed, as expected, that participants were more successful at solving problems that required the relaxation of lower order constraints (e.g., relaxing constraints on numerical value representation) than problems that required the relaxation of higher order constraints (e.g., relaxing constraints on arithmetic function representation). For example, after an average of 5 minutes, almost all participants solved problems requiring the relaxation of low-order constraints (Type A), whereas fewer than half of all participants solved problems requiring the relaxation of high-order constraints (Type C). In addition, participants were more successful at solving problems that required the decomposition of loose chunks (e.g., decomposing IV into I and V) than problems that required the decomposition of tight chunks (e.g., decomposing V into \ and /). After an average of 5 minutes, almost all participants solved problems requiring the decomposition of loose chunks (Type A), whereas only 75% of participants solved problems requiring the decomposition of tight chunks (Type D). Overcoming impasses in solving insight problems exemplifies a general need to override mental sets or fixed ways of thinking about problems generated from past experience with similar problems. The encumbrance of mental sets highlights the existence of factors such as how the problem is interpreted that can influence problem-solving success.

It is very likely that Oedipus solved the sphinx’s riddle by experiencing an insight into its solution. The riddle can certainly be labeled an ill-defined problem—one whose solution required the awareness of a key piece of information. What are the processes by which Oedipus gained the insight necessary to solve the riddle? This is an important question, but one whose answer remains a mystery. On the one hand, that any belief or thought can, in principle, be brought to bear on problem-solving endeavors permits the possibility of creative or insightful problem solving. On the other hand, because any belief or thought can be brought to bear on problem-solving endeavors, understanding how individuals select specific beliefs and thoughts as they solve problems remains a challenge—a challenge that we earlier identified as the frame problem (Fodor, 1983).

Factors that Mediate Problem Solving

Definition of Problem: Mental Set

A mental set involves thinking about a problem, its context, and its possible solution from a single perspective (Luchins, 1942; Sternberg, 1999). Such a limited perspective can hinder problem solving if a successful solution can be achieved only by viewing the problem from a novel angle. Setting the problem aside momentarily can foster insight or a new perspective (see earlier discussion of incubation effect) and help break the mental set. For example, misreading a word in an essay or misreading a variable in a mathematical proof can lead to a mental set and block understanding. In these cases, putting the material aside even for an hour and then coming back to it can break the mental set.

Past experience can be beneficial to problem solving, but it can also foster mental sets by biasing the way in which the problem solver ventures to reach a solution. In particular, expertise in the domain of the problem can actually disrupt problem solving, especially if the problem calls for a creative solution (Wiley, 1998). Although experts are generally able to solve problems in their domains more effectively than novices because their well-structured, easily activated knowledge permits an efficient search of the problem space, sometimes this knowledge can be disadvantageous. For example, Wiley (1998) has suggested that a large amount of domain knowledge can bias problem-solving efforts by confining the search space and therefore excluding the portion of the space in which the solution resides. That is, expertise can actually constrain creative problem solving by foreclosing the problem space prematurely (see also Bedard & Chi, 1992; Frensch & Sternberg, 1989).

Strategy Selection and Knowledge

Selecting the right strategy in response to a problem can determine whether a problem’s solution will be found and, if so, whether it will be found expeditiously. For example, the generate and test heuristic (Newell & Simon, 1972), which involves arbitrarily generating solution paths until the correct path is found, may ultimately lead one down the correct solution path, but it is not a very efficient strategy. In contrast, a working forward strategy is more efficient because it involves delimiting the set of possible solution paths and then choosing from this set the one that generates the better solution to the problem. Knowing which strategy to use in solving a given problem, however, is dependent on the problem solver’s level of expertise in the problem domain.

Not all strategies are used equally often by all problem solvers. Strategy selection depends on the problem domain and on the level of expertise of the problem solver within that domain (Chi et al., 1988). Expertise plays a pivotal role in strategy selection because greater domain knowledge in the domain of the problem influences the way in which the problem is interpreted, how the solution is envisioned, and hence the strategy that is ultimately selected to solve the problem. Bedard and Chi (1992), in a review of studies of expert problem solving, concluded that, in general, experts are better problem solvers than are novices because (a) they know more about their domain than do novices; (b) their knowledge is better organized in ways that make that knowledge more accessible, functional, and efficient; (c) they perform better than novices in domain-related tasks on the basis of their greater knowledge and better organization; and (d) their skills are domain specific. In short, experts select strategies and solve problems more efficiently than do novices.

Expert Problem Solving and Reasoning

The influential role of knowledge in successful problem solving has led investigators to examine closely the attributes of expert problem solvers (e.g., Charness & Schultetus, 1999; Ericsson, 1996; Ericsson & Charness, 1994; Ericsson & Smith, 1991; Sternberg, 1999). In contrast to the popular opinion that superior performance within a contextual domain originates solely from innate ability, research on expertise suggests that exceptional performance develops largely, although not exclusively, from intense preparation (Ericsson & Charness, 1994). Studies of expertise are intriguing because they suggest that human cognitive abilities are flexible and can adapt to meet increasingly higher expectations. Although research on expertise is integrated into the literature on problem solving (e.g., Chase & Simon, 1973; Chi et al., 1988; de Groot, 1965; Gobet, 1997; Holding, 1992), it is interesting that research on expertise has not been integrated into the literature on reasoning. As we will examine shortly, the absence of this integration may be a shortcoming in the field of reasoning.

Expertise is defined by Charness and Schultetus (1999) as “consistently superior performance on a set of representative tasks for the domain that can be administered to any subject” (p.58). Studies of expertise suggest that expert performance is a reliable phenomenon that can be measured using standard tasks or conditions for competition in laboratory settings (for a review, see Ericsson, 1996). Identified experts within a domain seem to share a cluster of features about their training and performance. First, peak performance results after many years of intense preparation and practice within the domain: 10,000 hours, for example, are normally required to reach toplevel performance within a domain (Charness & Schultetus, 1999). Second, experts do not simply spend more leisure time in their respective domain in comparison to others but, rather, spend more hours engaging in deliberate practice (Ericsson & Charness, 1994). Deliberate practice normally involves solitary study with the purpose of improving performance.

Expertise is associated with the ability to recognize important problem features quickly (Allard & Starkes, 1991; Chase & Simon, 1973; de Groot, 1965; Gobet, 1997; Gobet & Simon, 1996). For example, Gobet and Simon (1996) found that champion chess players could recall more than nine chess positions that had been presented to the players briefly and without breaks between presentations. Likewise, Allard and Starkes (1991) found that elite athletes were able to abstract and recall more information about game situations after a brief exposure than nonelite athletes. In sum, experts recognize meaningful relations or patterns in their domains of expertise (Gobet, 1997). Distilling such patterns allows experts to form complex representations of the problem situation, representations that integrate task information with background knowledge to select and evaluate actions and to consider alternative actions (Ericsson, 1996; Ericsson & Kintsch, 1995).

The Neglect of Expertise in Reasoning Theories

Although studies of expertise have been integrated into the problem-solving literature, these studies have not been integrated into the reasoning literature. For example, in tests of syntactic rule theory and mental model theory, participants who have training in logic or are considered expert reasoners on categorical and conditional syllogisms are excluded from participating. It is not entirely clear why participants with training in logic are excluded from participating in reasoning studies, but one reason seems to involve the belief that participants’ training will bias the study’s results. Participants without any training in logic (i.e., novices in logic) are usually included in studies of reasoning.

The systematic exclusion of expert reasoners from reasoning studies has likely obscured the rich variety of reasoning strategies available to individuals of different knowledge levels. Studying only how novices reason on a specific task makes it impossible to assess the full set of strategies available to reasoners with different knowledge levels: The full spectrum of responses is restricted. We know from research in expert problem solving that it is not uncommon for novices to resemble each other in their problem solving endeavors within a specific domain (e.g., Priest & Lindsay, 1992). However, that novices employ a single strategy on task X does not suggest that individuals with expertise on task X will use the same strategy or that novices will not use an alternate strategy on task Y. When both a restricted sample of participants (e.g., novices) and a restricted sample of tasks (e.g., categorical syllogisms) are used in reasoning studies, participants’strategies and responses might appear much more alike and consistent than they really are.

The neglect of expertise in reasoning studies might be a source of some ambiguity in theories of reasoning. Recall that at the beginning of this research paper we suggested that some ambiguity beset reasoning theories such as syntactic rule theory and mental model theory as to how syntactic rules and mental models should be conceptualized: that is, whether syntactic rules and mental models should be viewed as reasoning strategies or, more fundamentally, as mechanisms that comprise the cognitive architecture of the mind. Both syntactic rule theory andmentalmodeltheoryproposethatsyntacticrulesandmental models, respectively, comprise a fundamental mechanism in reasoning. In both theories, either rules or models are proposed to underlie reasoning, but not both. However, Stenning and Yule (1997) have indicated that rule-based and modelbased theories are essentially similar in their underlying logic but differ only as algorithms (cf. Falmagne & Gonsalves, 1995; Roberts, 1993; for a contrasting view see Over & Evans, 1999). Thus, rules and models are not mutually exclusive. We propose that some of the confusion regarding the cognitive status of syntactic rules and mental models—whether rules and models represent strategies or a fundamental reasoning mechanism—might be due to the nature of the participants and the tasks included in reasoning studies.When participants with no training in logic are tested on a restricted set of logical reasoning tasks (e.g., categorical and conditional syllogisms), results from reasoning studies show far more consistency in participants’ performance than there might be if participants withvaryinglevelsoftrainingwereincluded.Theconsistency in participants’performance might, mistakenly, lead syntactic rule supporters (or mental model supporters) to view rules (or models) as comprising a fixed or hard-wired mechanism in reasoning instead of a simple strategy.

Thematic Reasoning Tasks as Expert Tasks

Although participants with training in logic have been excluded from participating in reasoning studies, the influence of everyday expertise has not altogether been excluded. Paradoxically, the power of expertise in reasoning can be illustrated by examining performance on thematic reasoning tasks. Although the tasks in reasoning studies generally fail to reflect a substantive content domain, it is possible to view thematic reasoning tasks (e.g., thematic versions of the selection task) as reflecting a nominal, everyday content domain. When they are viewed thus, it is possible to consider thematic reasoning tasks as tests of everyday expertise—tests of everyday knowledge that most people possess in order to function successfully in everyday life. If we view thematic tasks as tests of everyday expertise, then it is not surprising that participants generally perform quite well on these tasks. Individuals might perform substantially better on thematic reasoning tasks than on abstract reasoning tasks because thematic tasks might cue their “expert” background knowledge, knowledge that is useful to their functioning in everyday life (e.g., Cosmides, 1989; Cummins, 1995). For example, most adults could easily be labeled experts at deontic reasoning— reasoning that involves knowing how to enforce a rule, catch rule violators, or understand what permissions and obligations entail.

Viewing competent performance on thematic reasoning tasks as evidence of everyday expertise is consistent with Cosmides’s (1989) social contract theory and Gigerenzer and Hug’s (1992) cheating detection theory. In fact, these theories might be better termed theories of everyday expertise without the need to incorporate post-hoc evolutionary claims. Social contract theory and cheating detection theory advance the idea that human beings are experts in domains that are essential to their survival (e.g., social exchange). These investigators claim that some domains are so fundamental to our survival that specific Darwinian algorithms have evolved to help us reason in those domains. In other words, in domains in which human beings must be knowledgeable in order to adapt and survive, expert algorithms have developed to guarantee successful reasoning. In short, it is possible that the facilitated performance observed on thematic versions of the selection task might serve as a clue that knowledge is power in reasoning as it is in problem solving and as early work on expert systems has made clear in the field of artificial intelligence (see Feigenbaum, 1989).

Because it appears that knowledge is power in reasoning, more studies need to explore how individuals with different knowledge levels perform on reasoning tasks that reflect a substantive content domain. In studying individuals with a range of knowledge, it will be possible to identify the strategies employed in reasoning and to determine whether myriad strategies characterize the reasoning of different groups of participants or whether a single strategy is employed by all participants on a specific task. It is premature at this stage to state that people reason primarily with mental models or mental rules or according to any other theory, given that a sizable group of participants (e.g., experts in logic) is excluded from reasoning studies of abstract categorical syllogisms and conditional syllogisms. If experts are included in reasoning studies, new evidence might illuminate the nature of reasoning. For example, new evidence for the use of rules in reasoning might be found by studying experts.

If neither rules nor models at present describe a fundamental reasoning mechanism or, alternatively, the representational mechanism in reasoning, then in what other form might reasoning be formalized? Borrowing from the literature on expertise, patterns might exemplify the representational mechanism in reasoning. The notion of patterns as a possible representational mechanism is not a new idea. For instance, Bechtel andAbrahamsen (1991) have suggested this idea, and numerous studies employing a connectionist methodology support the idea of patterns underlying reasoning. Patterns underlie reasoning in the sense that the pattern of connectivity in a PDPnetwork produces reliable responses to reasoning problems. Although it is beyond the scope of this research paper to review the role of patterns in reasoning, the interested reader is referred to studies in which connectionist methodology is used to model reasoning performance (e.g., Langston & Trabasso, 1999; Park & Robertson, 1997; Stenning & Oaksford, 1993; Stenning & Oberlander, 1995).

Summary and Conclusion

We will never know how the legendary Oedipus solved the sphinx’s riddle, but from our discussion thus far it is possible to speculate. First, it is unlikely that Oedipus either reasoned or problem solved exclusively in his search for a solution. He probably used a combination of methods. Having said this, however, we must add that it is likely that Oedipus used more problem solving techniques than reasoning techniques to generate the answer. In particular, because a riddle can be characterized as an ill-defined problem, it is likely that Oedipus experienced an insight into its solution. Of course, it is always possible that he used some kind of strategy.

It seems trite to say that investigators of reasoning and problem solving have a great deal to learn from each other. It is true, however, and it is especially relevant as we attempt to further our understanding of how knowledge influences—for better or for worse—our reasoning on everyday tasks. Research on expertise offers an optimistic view that thinking, problem solving, reasoning, and other activities are not controlled solely by innate abilities. Deliberate practice and training can improve our performance. Expertise, the idea that performance evolves with practice, should be incorporated into theories of reasoning so as to delineate fully how individuals reason at different times with different levels of knowledge. One risk of excluding expert reasoners, as has been the case in studies of logical reasoning, is that participants’ performance on reasoning tasks might appear to be overly consistent. The apparent consistency in participants’ performance might be illusory and misleading, leading to the ambiguity and entanglement of reasoning strategies with a fundamental reasoning mechanism. Because the responses of untrained logical reasoners appear consistent, investigators might mistakenly attribute these responses to a fundamental reasoning mechanism, when in fact they might only represent the application of strategies. Stenning and Yule (1997) have suggested that rules and models should be viewed as algorithms and not as anything more fundamental than that. Failing to test participants who reflect a range of knowledge levels on reasoning tasks constrains the likelihood of capturing and examining the full range of strategies and solutions generated to reasoning tasks. Ultimately, our understanding is also constrained.

The literature on expertise, furthermore, leads us to conclude that pattern recognition might serve as a representational mechanism in reasoning. Connectionist studies of reasoning exemplify a pattern-recognition approach, but the challenge is to interpret precisely how connectionist architectures solve reasoning problems (Dawson, 1998). Only by interpreting connectionist models can we validate that their algorithms for solving problems are psychologically plausible (Berkeley, Dawson, Medler, Schopflocher, & Hornsby, 1995; Dawson, 1998; Oaksford & Chater, 1993).

The future challenge for investigators of reasoning, more so than for investigators of problem solving, is to (a) clarify how strategies differ from representational mechanisms in reasoning and (b) further our understanding of how knowledge mediates reasoning. If the goal of experimental laboratory studies of reasoning and problem solving is to gain a better understanding of how people reason and problem solve in everyday contexts, then background knowledge must be a fundamental variable in studies of reasoning and problem solving. In the end, a more solid understanding of how everyday reasoning and problem solving operate has tremendous social benefits in a variety of contexts—educational, professional, political, legal, and medical—in which we aim to improve performance. Indeed, knowledge is power.

Bibliography:

1. Allard, F., & Starkes, J. L. (1991). Motor-skill experts in sports, dance, and other domains. In K. Anders Ericsson & Jacqui Smith (Eds.), Toward a general theory of expertise: Prospects and limits (pp. 126–152). New York: Cambridge University Press.
2. Anderson, J. R. (1983). The architecture of cognition. Cambridge, MA: Harvard University Press.
3. Anderson, J. R. (1990). Cognitive psychology and its implications (3rd ed.). New York: W. H. Freeman.
4. Bechtel, W., & Abrahamsen, A. (1991). Connectionism and the mind. Cambridge, MA: Blackwell.
5. Bedard, J., & Chi, M. T. (1992). Expertise. Current Directions in Psychological Science, 1, 135–139.
6. Berkeley, I. S. N., Dawson, M. R. W., Medler, D. A., Schopflocher, D. P., & Hornsby, L. (1995). Density plots of hidden value unit activations reveal interpretable bands. Connection Science, 7, 167–186.
7. Blanchette, I., & Dunbar, K. (2000). How analogies are generated: The role of structural and superficial similarity. Memory & Cognition, 28, 108–124.
8. Braine, M. D. S. (1978). On the relation between the natural logic of reasoning and standard logic. Psychological Review, 85, 1–21.
9. Braine, M. D. S., & O’Brien, D. P. (1991). A theory of If: A lexical entry, reasoning program, and pragmatic principles. Psychological Review, 98, 182–203.
10. Braine, M. D. S., & O’Brien, D. P. (1998). The theory of mentalpropositional logic: Description and illustration. In M. D. S. Braine & D. P. O’Brien (Eds.), Mental logic (pp. 79–89). Mahwah, NJ: Erlbaum.
11. Braine, M. D. S., Reiser, B. J., & Rumain, B. (1998). Evidence for the theory: Predicting the difficulty of propositional logic inference problems. In M. D. S. Braine & D. P. O’Brien (Eds.), Mental logic (pp. 91–144). Mahwah, NJ: Erlbaum.
12. Braine, M. D. S., & Rumain, B. (1983). Logical reasoning. In P. H. Mussen (Series Ed.) & J. H. Flavell & E. M. Markman (Vol. Eds.), Handbook of child psychology: Vol. 3. Cognitive development (4th ed., pp. 263–340). New York: Wiley.
13. Brunswick, E. (1943). Organismic achievement and environmental probability. Psychological Review, 50, 255–272.
14. Charness, N., & Schultetus, R. S. (1999). Knowledge and expertise. In F. T. Durso, R. S. Nickerson, R. W. Schvaneveldt, S. T. Dumais, D. S. Lindsay, & M. Chi (Eds.), Handbook of applied cognition (pp. 57–81). Chichester, England: Wiley.
15. Chase, W. G., & Simon, H. A. (1973). Perception in chess. Cognitive Psychology, 4, 55–81.
16. Chater, N., & Oaksford, M. (1999). The probability heuristics model of syllogistic reasoning. Cognitive Psychology, 38, 191–258.
17. Cheng, P. W., & Holyoak, K. J. (1985). Pragmatic reasoning schemas. Cognitive Psychology, 17, 391–416.
18. Cheng, P. W., & Holyoak, K. J. (1989). On the natural selection of reasoning theories. Cognition, 33, 285–313.
19. Cheng, P. W., & Nisbett, R. E. (1993). Pragmatic constraints on causal deduction. In R. E. Nisbett (Ed.), Rules for reasoning (pp. 202–227). Hillsdale, NJ: Erlbaum.
20. Chi, M. T. H., Glaser, R., & Farr, M. J. (Eds.). (1988). The nature of expertise. Hillsdale, NJ: Erlbaum.
21. Cosmides, L. (1989). The logic of social exchange: Has natural selection shaped how human reason? Studies with the Wason selection task. Cognition, 31, 187–276.
22. Cosmides, L., & Tooby, J. (1996). Are humans good intuitive statisticians after all? Rethinking some conclusions from the literature on judgement under uncertainty. Cognition, 58, 1–73.
23. Cummins, D. D. (1995). Naïve theories and causal deduction. Memory & Cognition, 23, 646–658.
24. Davidson, J., & Sternberg, R. J. (1984). The role of insight in intellectual giftedness. Gifted Child Quarterly, 28, 58–64.
25. Dawson, M. R. W. (1998). Understanding cognitive science. Malden, MA: Blackwell.
26. Dawson, M. R. W., Medler, D. A., & Berkeley, I. S. N. (1997). PDP networks can provide models that are not mere implementations of classical theories. Philosophical Psychology, 10, 25–40.
27. de Groot, A. D. (1965). Thought and choice in chess. The Hague, The Netherlands: Mouton.
28. Dennett, D. (1990). Cognitive wheels: The frame problem of AI. In M. Boden (Ed.), The philosophy of artificial intelligence: Oxford readings in philosophy (pp. 147–170). Oxford, UK: Oxford University Press.
29. Dietrich, E. (1999). Algorithm. In R. A. Wilson & F. C. Keil (Eds.), The MIT encyclopedia of the cognitive sciences (pp. 11–12). Cambridge, MA: MIT Press.
30. Dominowski, R. L., & Jenrick, R. (1973). Effects of hints and interpolated activity on solution of an insight problem. Psychonomic Science, 26, 335–338.
31. Dunbar, K. (1995). How scientists really reason: Scientific reasoning in real-world laboratories. In R. J. Sternberg & J. E. Davidson (Eds.), The nature of insight (pp. 365–395). Cambridge, MA: MIT Press.
32. Dunbar, K. (1997). How scientists think: On-line creativity and conceptual change in science. In T. B. Ward & S. M. Smith (Eds.), Creative thought: An investigation of conceptual structures and processes (pp. 461–493). Washington, DC: American Psychological Association.
33. Eisenstadt, S. A., & Simon, H. A. (1997). Logic and thought. Minds & Machines, 7, 365–385.
34. Ericsson, K. A. (1996). The acquisition of expert performance. In K. A. Ericsson (Ed.), The road to excellence. Mahwah, NJ: Erlbaum.
35. Ericsson, K. A., & Charness, N. (1994). Expert performance: Its structure and acquisition. American Psychologist, 49, 725–747.
36. Ericsson, K. A., & Kintsch, W. (1995). Long-term working memory. Psychological Review, 102, 211–245.
37. Ericsson, K. A., & Smith, J. (1991). Prospects and limits in the empirical study of expertise: An introduction. In K. A. Ericsson & J. Smith (Eds.), Toward a general theory of expertise: Prospects and limits (pp. 1–38). Cambridge, UK: Cambridge University Press.
38. Evans, J. St. B. T. (1989). Bias in human reasoning: Causes and consequences. Hillsdale, NJ: Erlbaum.
39. Evans, J. St. B. T. (2000). What could and could not be a strategy in reasoning. In W. Schaeken, G. De Vooght, A. Vandierendonck, & G. d’Ydewalle (Eds.), Deductive reasoning and strategies (pp. 23–48). Mahwah, NJ: Erlbaum.
40. Evans, J. St. B. T., Handley, S. J., Harper, C. N. J., & Johnson-Laird, P. N. (1999). Reasoning about necessity and possibility: Atest of the mental model theory of deduction. Journal of Experimental Psychology: Learning, Memory, and Cognition, 25, 1495–1513.
41. Evans, J. St. B. T., & Lynch, J. S. (1973). Matching bias in the selection task. British Journal of Psychology, 64, 391–397.
42. Evans,St.B.T.,Newstead,S.E.,&Byrne,R.M.(1993).Humanreasoning: The psychology of deduction. Hillsdale, NJ: Erlbaum.
43. Evans,J.St.B.T.,Over,D.E.,&Manktelow,K.I.(1993).Reasoning, decision making, and rationality. Cognition, 49, 165–187.
44. Falmagne, R. J., & Gonsalves, J. (1995). Deductive inference. Annual Review of Psychology, 46, 525–559.
45. Feigenbaum, E.A. (1989).What hath Simon wrought? In D. Klahr & K. Kotovsky (Eds.), Complex information processing: The impact of Herbert A. Simon (pp. 165–182). Hillsdale, NJ: Erlbaum.
46. Fischhoff, B. (1999). Judgement heuristics. In R. A. Wilson & F. C. Keil (Eds.), The MIT encyclopedia of the cognitive sciences (pp. 423–425). Cambridge, MA: MIT Press.
47. Fodor, J. A. (1983). The modularity of mind. Cambridge, MA: MIT Press.
48. Ford, M. (1995). Two models of mental representation and problem solving in syllogistic reasoning. Cognition, 54, 1–71.
49. Frensch, P. A., & Sternberg, R. J. (1989). Expertise and intelligent thinking: When is it worse to know better? In R. J. Sternberg (Ed.), Advances in the psychology of human intelligence (Vol. 5, pp. 157–188). Hillsdale, NJ: Erlbaum.
50. Galotti, K. M. (1989). Approaches to studying formal and everyday reasoning. Psychological Bulletin, 105, 331–351.
51. Galotti, K. M., Baron, J., & Sabini, J. P. (1986). Individual differences insyllogisticreasoning:Deductionrulesormentalmodels? Journal of Experimental Psychology: General, 115, 16–25.
52. Garnham, A., & Oakhill, J. (1994). Thinking and reasoning. Cambridge, MA: Blackwell.
53. Gentner, D. (1983). Structure-mapping: Atheoretical framework for analogy. Cognitive Science, 7, 155–170.
54. Gentner, D. (1999). Analogy. In R. A. Wilson & F. C. Keil (Eds.), The MIT encyclopedia of the cognitive sciences (pp. 17–19). Cambridge, MA: MIT Press.
55. Gentner, D., Rattermann, M. J., & Forbus, K. D. (1993). The roles of similarity in transfer: Separating retrievability from inferential soundness. Cognitive Psychology, 25, 524–575.
56. Gigerenzer, G., & Hug, K. (1992). Domain-specific reasoning: Social contracts, cheating, and perspective change. Cognition, 43, 127–171.
57. Gigerenzer, G., Todd, P. M., & the ABC Research Group. (Eds.). (1999). Simple heuristics that make us smart. New York: Oxford University Press.
58. Greene, S. B. (1992). Multiple explanations for multiply quantified sentences: Are multiple models necessary? Psychological Review, 99, 184–187.
59. Griggs,R.A.(1983).Theroleofproblemcontentintheselectiontask.In J. St. B. T. Evans (Ed.), Thinking and reasoning: Psychological approaches(pp. 16–43).London:RoutledgeandKeganPaul.
60. Gobet, F. (1997). A pattern-recognition theory of search in expert problem solving. Thinking and Reasoning, 3, 291–313.
61. Gobet, , & Simon, H. A. (1996).Templates in chess memory: Amechanism for recalling several boards. Cognitive Psychology, 31, 1–40.
62. Guyote, M. J., & Sternberg, R. J. (1981). A transitive-chain theory of syllogistic reasoning. Cognitive Psychology, 13, 461–525.
63. Holding, D. H. (1992). Theories of chess skill. Psychological Research, 54, 10–16.
64. Holland, J. H., Holyoak, K. J., Nisbett, R. E., & Thagard, P. R. (1986). A framework for induction. Induction: Processes of inferences, learning, and discovery (pp. 1–28). Cambridge, MA: MIT Press.
65. Holyoak, K. J. (1990). Problem solving. In D. N. Osherson & E. E. Smith (Eds.), Thinking: An invitation to cognitive science (Vol. 3, pp. 117–146). Cambridge, MA: MIT Press.
66. Johnson-Laird, P. N. (1983). Mental models. Towards a cognitive science of language, inference, and consciousness. Cambridge, MA: Harvard University Press.
67. Johnson-Laird, P. N. (1994). Mental models and probabilistic thinking. Cognition, 50, 189–209.
68. Johnson-Laird, P. N. (1999). Deductive reasoning. Annual Review of Psychology, 50, 109–135.
69. Johnson-Laird, P. N., & Bara, B. G. (1984). Syllogistic inference. Cognition, 16, 1–61.
70. Johnson-Laird, P. N., & Byrne, R. M. J. (1991). Hillsdale, NJ: Erlbaum.
71. Johnson-Laird,P.N.,Byrne,R.M.J.,&Schaeken,W.(1992).Propositional reasoning by model. Psychological Review, 99, 418–439.
72. Knoblich, G., Ohlsson, S., Haider, H., & Rhenius, D. (1999). Constraint relaxation and chunk decomposition in insight problem solving. Journal of Experimental Psychology: Learning, Memory, and Cognition, 25, 1534–1555.
73. Langston, M., & Trabasso, T. (1999). Modeling causal integration and availability of information during comprehension of narrative texts. In H. van Oostendorp & S. Goldman (Eds.), The construction of mental representations during reading (pp. 29– 69). Mahwah, NJ: Erlbaum.
74. Lehman, J. F., Lewis, R. L., & Newell, A. (1998). Architectural influences on language comprehension. In Z. Pylyshyn (Ed.), Constraining cognitive theories (pp. 141–163). Stamford, CT: Ablex Publishing.
75. Leighton, J. P., & Dawson, M. R. W. (2001). A parallel distributed processing model of Wason’s selection task. Cognitive Systems Research, 2, 207–231.
76. Liberman, N., & Klar, Y. (1996). Hypothesis testing in Wason’s selection task: Social exchange, cheating detection, or task understanding. Cognition, 58, 127–156.
77. Light, P., Girotto, V., & Legrenzi, P. (1990). Children’s reasoning on conditional promises and permissions. Cognitive Development, 5, 369–383.
78. Luchins, A. S. (1942). Mechanization in problem solving—the effect of Einstellung. Psychological Monographs, 54 (Serial No. 6, 95).
79. Manktelow, K. I., & Evans, J. St. B. T. (1979). Facilitation of reasoning by realism: Effect or non-effect? British Journal of Psychology, 70, 477–488.
80. Manktelow, K. I., Fairley, N., Kilpatrick, S. G., & Over, D. E. (2000). Pragmatics and strategies for practical reasoning. In W. Schaeken, G. De Vooght, & G. d’Ydewalle (Eds.), Deductive reasoning and strategies (pp. 23–48). Mahwah, NJ: Erlbaum.
81. Manktelow, K. I., & Over, D. E. (1991). Social roles and utilities in reasoning with deontic conditionals. Cognition, 39, 85–105.
82. Metcalfe, J. (1986). Premonitions of insight predict impending error. Journal of Experimental Psychology: Learning, Memory, and Cognition, 12, 623–634.
83. Metcalfe, J. (1998). Insight and metacognition. In G. Mazzoni & T. Nelson (Eds.), Metacognition and cognitive neuropsychology: Monitoring and control processes (pp. 181–197). Mahwah, NJ: Erlbaum.
84. Metcalfe, J., & Wiebe, D. (1987). Intuition in insight and noninsight problem solving. Memory & Cognition, 3, 238–246.
85. Newell, A. (1990). Unified theories of cognition. Cambridge, MA: Harvard University Press.
86. Newell, A., & Simon, H. A. (1972). Human problem solving. Englewood Cliffs, NJ: Prentice-Hall. .
87. Newstead, S. E., & Evans, J. St. B. T. (1993), Mental models as an explanation of belief bias effects in syllogistic reasoning. Cognition, 46, 93–97.
88. Noveck, I., & O’Brien, D. P. (1996). To what extent do pragmatic reasoning schemas affect performance on Wason’s selection task? Quarterly Journal of Experimental Psychology: Human Experimental Psychology, 49A, 463–489.
89. O’Brien, D. P. (1993). Mental logic and human irrationality: We can put a man on the moon, so why can’t we solve those logicalreasoning problems? In K. I. Manktelow & D. E. Over (Eds.), Rationality: Psychological and philosophical perspectives (pp. 110–135) London: Routledge.
90. Oaksford, M., & Chater, N. (1993). Reasoning theories and bounded rationality. In K. I. Manktelow & D. E. Over (Eds.), Rationality: Psychological and philosophical perspectives (pp. 31–60). London: Routledge.
91. Oaksford, M., & Chater, N. (1994).Arational analysis of the selection taskasoptimaldataselection.PsychologicalReview,101,608–631.
92. Over, D. E., & Evans, J. St. B. T. (1999). The meaning of mental logic. Cahiers de Psychologie, 18, 99–104.
93. Park, N. S., & Robertson, D. (1997). A localist network architecture for logical inference. In R. Sun & F. Alexandre (Eds.), Connectionist-symbolic integration: From unified to hybrid approaches (pp. 245–263). Mahwah, NJ: Erlbaum.
94. Polk, T. A., & Newell, A. (1995). Deduction as verbal reasoning. Psychological Review, 102, 533–566.
95. Pollard, P. (1990). Natural selection for the selection task: Limits to social-exchange theory. Cognition, 36, 195–204.
96. Pollard, P., & Evans, J. St. B. T. (1987). Content and context effects in reasoning. American Journal of Psychology, 100, 41–60.
97. Priest, A. G., & Lindsay, R. O. (1992). New light on novice-expert differences in physics problem solving. British Journal of Psychology, 83, 389–405.
98. Rips, L. J. (1994). The psychology of proof. Cambridge, MA: MIT Press.
99. Rips, L. J. (1995). Deduction and cognition. In E. E. Smith & D. N. Osherson (Eds.), Thinking: Vol. 3. An invitation to cognitive science (2nd ed., pp. 297–343). Cambridge, MA: MIT Press.
100. Roberts, M. J. (1993). Human reasoning: Deduction rules or mental models, or both? Quarterly Journal of Experimental Psychology, 46A, 569–589.
101. Roberts, J. (2000). Individual differences in reasoning strategies: A problem to solve or an opportunity to seize? In W. Schaeken, G. De Vooght, A. Vandierendonck, & G. d’Ydewalle (Eds.), Deductive reasoning and strategies (pp. 23–48). Mahwah, NJ: Erlbaum.
102. Rumain, B., Connell, J., Braine, M. D. S. (1983). Conversational comprehension processes are responsible for reasoning fallacies in children as well as adults: If is not the biconditional. Developmental Psychology, 19, 471–481.
103. Schaeken, W., De Vooght, G., Vandierendonck, A., & d’Ydewalle, G. (Eds.). (2000). Deductive reasoning and strategies. Mahwah, NJ: Erlbaum.
104. Shepard, R. N. (1990). Mind sights. New York: W. H. Freeman.
105. Simon, H. A. (1991). Cognitive architectures and rational analysis: Comment. In K. VanLehn (Ed.), Architectures for intelligence (pp. 25–39). Hillsdale, NJ: Erlbaum.
106. Simon, H. A. (1999a). Problem solving. In R. A. Wilson & F. C. Keil (Eds.), The MIT encyclopedia of the cognitive sciences (pp. 674–676). Cambridge, MA: MIT Press.
107. Simon, H. A. (1999b). Production systems. In R. A. Wilson & F. C. Keil (Eds.), The MIT encyclopedia of the cognitive sciences (pp. 676–677). Cambridge, MA: MIT Press.
108. Smith, S. M., & Blankenship, S. E. (1989). Incubation effects. Bulletin of the Psychonomic Society, 27, 311–314.
109. Sperber, D., Cara, F., & Girotto, V. (1995). Relevance theory explains the selection task. Cognition, 57, 31–95.
110. Stenning, K., & Oaksford, M. (1993). Rational reasoning and human implementations of logic. In K. I. Manktelow & D. E. Over
111. (Eds.), Rationality: Psychological and philosophical perspectives (pp. 136–176). Florence, KY: Taylor & Francis/Routledge.
112. Stenning, K., & Oberlander, J. (1995). A cognitive theory of graphical and linguistic reasoning: Logic and implementation. Cognitive Science, 19, 97–140.
113. Stenning, K., &Yule, P. (1997). Image and language in human reasoning: A syllogistic illustration. Cognitive Psychology, 34, 109–159.
114. Sternberg, R. J. (1980a). Representation and process in linear syllogistic reasoning. Journal of Experimental Psychology: General, 109, 119–159.
115. Sternberg, R. J. (1980b). The development of linear syllogistic reasoning. Journal of Experimental Child Psychology, 29, 340–356.
116. Sternberg, R. J. (1981). Reasoning with determinate and indeterminatelinearsyllogisms.BritishJournalofPsychology,72,407–420.
117. Sternberg, R. J. (1983). Components of human intelligence. Cognition, 15, 1–48.
118. Sternberg, R. J. (1999). Cognitive psychology (2nd ed.). Ft. Worth, TX: Harcourt Brace.
119. Sternberg, R. J., & Ben Zeev, T. (2001). Complex cognition: The psychology of human thought. New York: Oxford University Press.
120. Sternberg, R. J., & Davidson, J. E. (Eds.). (1995). The nature of insight. Cambridge, MA: MIT Press.
121. Torrens, D., Thompson, V. A., & Cramer, K. M. (1999). Individual differences and the belief bias effect: Mental models, logical necessity, and abstract reasoning. Thinking and Reasoning, 5, 1–28.
122. Tversky, A., & Kahneman, D. (1974). Judgement under uncertainty: Heuristics and biases. Science, 185, 1124–1131.
123. Tversky, A., & Kahneman, D. (1986). Judgment under uncertainty: Heuristics and biases. In H. R. Arkes & K. R. Hammond (Eds.), Judgment and decision making: An interdisciplinary reader (pp. 38–55). Cambridge, UK: Cambridge University Press.
124. Wason, P. C. (1966). Reasoning. In B. M. Foss (Ed.), New horizons in psychology (pp. 135–151). Harmondsworth, Middlesex, England: Penguin.
125. Wason, P. C. (1983). Realism and rationality in the selection task. In J. St. B. T. Evans (Ed.), Thinking and reasoning: Psychological approaches (pp. 44–75). London: Routledge & Kegan Paul.
126. Wason, P. C., & Johnson-Laird, P. N. (1972). Psychology of reasoning: Structure and content. Cambridge, MA: Harvard University Press.
127. Wiley, J. (1998). Expertise as mental set: The effects of domain knowledge in creative problem solving. Memory & Cognition, 26, 716–730.