Rates Of The First And Second Kind Research Paper

1. Summary Measures For A Cohort

As in Demographic Techniques: LEXIS Diagram, let members of a given birth cohort have an intensity or risk function λ(x) at exact age x for an event of interest. If the event is repeatable (like the birth of a child), the integral ∫b λ(x) dx would be the mean number of such events between exact ages a and b to a cohort member if there were no mortality and out-migration. This interesting integral can be estimated by adding up the age-specific occurrence exposure rates over ages from a through b-1 in the cohort in question.

For a nonrepeatable event with the risk function λ(x), the quantity _b−aqa =1 -exp {-∫b λ(x) dx} would be the corresponding probability of experiencing the event before exact age b for a cohort member who had not experienced the event by exact age a. The integral ∫ba λ(x) dx plays a central role for the analysis of nonrepeatable events as well, but its function is quite different from the corresponding integral for a repeatable event.

The probability _b−aq_a may be estimated in two different manners, as follows.

(a) If a sequence of age-specific rates of the first kind is available for a cohort, adding them up for ages a through b-1 produces an estimate I of ∫a λ(x) dx, from which an estimate _b−aq_a =1 -exp {- I} of _b−aq_a can be computed.

(b) If a sequence of age-specific rates of the second kind is available for the cohort, then adding them up over ages a to b – 1 produces a sum that is an estimate a directly. This simple fact had been understood intuitively for many years before it was proved in great generality in a sequence of papers by Hoem (1978), Finnas (1980), and Borgan and Ramlau-Hansen (1985).

While we have described summary measures by aggregation over age for birth cohorts, similar aggregation is equally meaningful for other kinds of cohorts when age is replaced by duration since the formation of the cohort. For example, marital fertility rates can be computed by marriage duration, and adding them up over duration produces corresponding summary measures for marriage cohorts. It will not be equally meaningful to aggregate marital fertility rates across age groups, for not all members of a marriage cohort are at ‘risk’ of childbearing from the lowest age at marriage, simply because some marry at a later age.

2. Summary Measures For A Period

2.1 The Total Fertility Rate

Formally, summary measures can be computed for a calendar year, say, by aggregating over age in the same manner as for a cohort. The resulting period index is often said to be computed for a synthetic cohort. For a repeatable event the index is called a total rate, such as the total fertility rate, which is computed by adding up age-specific fertility rates for a calendar year over all ages.

As was pointed out by Hajnal (1947) already, it is important not to misunderstand the meaning of such a period index. The total fertility rate of year n is expressed in the same units as a cohort completed fertility (CCF), namely as an average number of children per woman, but it is not even some sort of average of the CCFs of the cohorts who are at fertile ages during year n. In fact the TFRⁿ for year n may even lie outside the range of the corresponding CCFs. To see what TFRn actually is, suppose that the rates are computed by age attained in vertical-sided parallelograms (see Fig. 3(a) in Demographic Techniques: LEXIS Diagram). Let Pn be the number of women at age i at the beginning of year n, let Rn be the number of person-years recorded for women who attain age i during the year, and let Bn be the number of liveborn children to these women during the year. (Rn must perhaps be approximated by (Pⁿ_t-1 +P^{n+ 1} )/2.) Then the corresponding birth rate is fi =Bi/Ri and B= ∑i Bn is the total number of liveborn children to women of all ages. A trivial calculation shows that

where

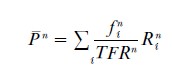
is a weighted average of the mean sizes of the cohorts of women who are at fertile ages during year n. Thus, TFRⁿ=Bⁿ/Pⁿ, which means that as of a fashion the total fertility rate can be seen as the number of births in year n per woman in the cohorts who are at fertile ages during that year.

The value of the total fertility rate has been around 1.4 children per woman for the European Union as a whole over a number of recent years. This means that annual cohorts of newly-born children in the EU have been one-third smaller than the mean total numbers in generations of young female adults during the same years (for 1.4/2.1 =2/3). If we disregard the effect of female mortality before age 30 (which has become very low today), the total number of adults at age 30 in about 30 years will be

(a) one-third lower than the mean total number of young adults in the baseline period (‘today’) if there is no net migration in the meantime;

(b) equal to the mean total number of young adults in the resident population today if net in-migration leads to a percentage of in-migrants one-third higher than the corresponding proportion of out-migrants born in the given area;

(c) lower than, equal to, or larger than the mean total number of young adults today according to the net percentage of in-migrants in the resident population.

In other words, compared to the present situation there will be a reduction in the total number of adults within a generation if net migration leads to a percentage of in-migrants less than approximately the rate of out-migration plus one-third.

2.2 The Total First-Marriage Rate

The total first-marriage rate (TFMR) has a similar meaning. It is computed as the sum of age-specific first-marriage rates of the second kind for a given calendar year. A TFMR of 0.5 is close to the values commonly observed in Europe nowadays, and it means that the number of single women who get married during the year is half the average size of female cohorts who are at the ages of first marriage. An observed low value, say, of the TFMR may result from a low average level of nuptiality during the year, or alternatively from a high nuptiality in corresponding cohorts in previous, and possibly in subsequent, years.

The (period-based) total first-marriage rate computed from rates of the second kind may well exceed 1, despite the fact that no one can enter first marriage more than once. For cases in point, see for instance Vogt (1964). The corresponding total first-birth rates were above 1 in many countries during the baby-boom years after World War II. See Whelpton (1954) for the United States, for instance. A corresponding cohort-based aggregate rate can never exceed 1, nor can the single-decrement computation of the proportion ever married (or of the proportion who ever get a first birth) in a synthetic cohort based on first-marriage rates of the first kind for a calendar year ever produce such a value. The rates of the first kind for a calendar year may add up to more than 1, but this only means that the corresponding probability ω−αqα is larger than 1 –e^-1≈ 0.63 (when λ(x)>0 only for α<x<ω).

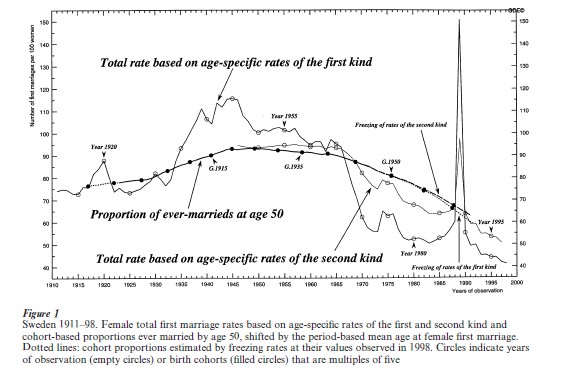
Figure 1 contains total rates of first marriage (based on rates of the second kind) for women in Sweden for calendar years 1946 through 1977 along with corresponding proportions ever married by age 50 for cohorts born in 1890 through 1960. (For cohorts born after 1948 marriage rates at higher ages have been estimated.) The plot also contains aggregated first-marriage rates of the first kind (similarly called corresponding ‘total rates’ on the graph) for years 1911 through 1998. None of the total rates of the second kind exceed 1 in this draft, but many of the ‘total rates’ of the first kind do and often indicate a period-based value of ₃₅q₁₅ in excess of 2/3. (We have used α =15 and ω=50 in these computations.) There was a huge peak in Swedish nuptiality in 1989 caused by a change in the regulations concerning public widow’s pensions that led a substantial number of couples to marry before the end of the year, particularly among cohabiting partners (Hoem 1991).

3. Conversion Of Rates Of The First Kind Into Rates Of The Second Kind, And Vice Versa, For Birth Cohorts

It is useful to be able to convert cohort rates of one kind into corresponding rates of the other kind, both ways. Consider therefore a nonrepeatable event like first marriage, and let pⁿ be its rate of the second kind and πⁿ the rate of the first kind, both observed at age i during year n. Suppose that the population is closed and that there is no death and no migration in the age bracket [α, ω], α being the minimum legal age at marriage for the sex under consideration and ω being age 50 as before. Moreover, to be concrete let us assume that these rates are expressed in terms of age attained during the year.

The proportion never married at the beginning of year n among persons then of completed age i-1 can be computed in two equivalent ways, and we get

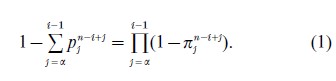
If we write out the same relation for a year later and subtract the latter from Eqn. (1) we obtain the following formula to convert π rates into p rates:

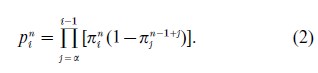
If we divide the initial identity for year n+1 by that for year n and reorganize, we get, conversely, the following formula to transform p rates into π rates:

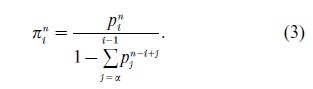
The total rate for year n, based on rates of the first kind is

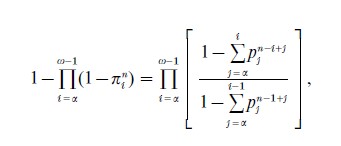
which differs from the similar total rate for year n based on rates of the second kind, namely,

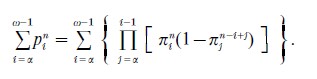
This does not prevent the aggregate rate of occurrence of the event in question for the cohort born during any year G to be the same for either kind of rates:

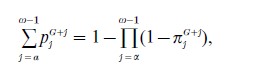
as in Eqn. (1) with i =ω and G =n -i.

The derivation of Eqn. (3) is a simplification of material already in the literature (Shryock and Siegel (1976 p. 292, formula 32), Finnas (1980), Borgan and Ramlau-Hansen (1985)).

In the equations above, we have disregarded migration and mortality. In an open population, these relationships hold only if disturbing phenomena (migration and death) are independent of the event under study. For example, if the event is first marriage, this assumption essentially means that the proportion ever married among in-migrants arriving at age x is the same as in the nonmigrant population of the same age, and that never-married immigrants arriving at age x have the same propensity to marry according to age as nonmigrants in the host country. Moreover, it pre-supposes that only a negligible number of in-migrants who arrived as never-married marry in their home country while residents of the host country and have their marriage go undetected by the vital registration system of the host country. In some cases these latter issues are unproblematic (Finnas 1980).

Bibliography:

1. Borgan Ø, Ramlau-Hansen H 1985 Demographic incidence rates and estimation of intensities with incomplete information. Annals of Statistics 13: 564–82
2. Finnas F 1980 A method to estimate demographic intensities via cumulative incidence rates. Theoretical Population Biology 17: 365–79
3. Hajnal J 1947 The analysis of birth statistics in the light of the recent international recovery of the birth-rate. Population Studies 1: 137–64
4. Hoem J M 1978 Demographic incidence rates. Theoretical Population Biology 14: 329–37
5. Hoem J M 1991 To marry, just in case …: the Swedish widow’s pension reform and the peak in marriages in December 1989.
6. Shryock H S, Siegel J S et al. 1976 The Methods and Materials of Demography [Condensed Edition by E. G. Stockwell]. Academic Press, San Diego, CA
7. Vogt J 1964 Component parts of the number of birth. Statsøkonomisk Tidsskrift 78: 287–307
8. Whelpton P K 1954 Cohort Fertility: Native White Women in the United States. Princeton University Press, Princeton, NJ