Indirect Estimation Research Paper

For conceptual purposes, it is useful to divide estimation techniques into two broad families. One family consists of true indirect estimation techniques. The strategy underlying indirect techniques is to find a readily measurable indicator that is largely, but not entirely, determined by the parameter of interest. Simulations developed using demographic models are then used to explore the relationship between the indicator and the parameter of interest, and to develop a simple approach to adjusting the indicator for other confounding factors, to provide a pure esti-mate of the parameter itself. An example of such an indicator is the proportion of dead among children ever borne by women of a given age group. This proportion is an indicator of the level of child mortality, but it is also affected by the age pattern of childbearing.

The second family is made up of consistency checks. Different indicators of the same demographic process are compared, either using models or formal demo-graphic relationships. Differences are interpreted as indications of data error. Assumptions about the nature of data errors can sometimes justify adjustment of one set of indicators for presumed error in order to arrive at an improved overall estimate of the under-lying process.

1. Indirect Methods

Reverse projection can be used to estimate recent aggregate fertility levels from the population age structure by allowing for mortality. The approach has a long history, but has not proved particularly useful. First, a common error in age distributions is for the population under age five years, to be under-recorded. This error causes recent fertility estimates based on reverse projection, to be too low. Second, the method is sensitive to the assumption of no (or not known) migration. Third, mortality rates have to be known at least approximately. Fourth, the fertility indicator estimated is the birth rate or General Fertility Rate; no detail about age patterns of fertility is provided.

This last shortcoming is avoided by the ‘Own Children’ variant of reverse projection (Cho et al. 1986). Children are matched to a likely mother within each household using criteria such as age and parity. Information on age of child provides a time period for the fertility measure, and in combination with age of putative mother provides the age of the mother at the time of the birth. Unmatched children are distributed proportionately, and both children and women are reverse-projected using appropriate mortality estimates. A suitably-matched age distribution thus pro- vides estimates of age-specific fertility rates for calendar years prior to the census or survey. Results remain sensitive to age reporting errors, however, and the other problems of standard reverse projection.

Fitting stable population models to an observed age distribution in combination with one other indicator such as the population growth rate or probability of dying by age five years represents another way of indirectly estimating fertility. Stable population analysis is of limited value today, because widespread declining fertility has affected age distributions world-wide. Preston (1983) has developed an elegant approach based on a generalized equation of age structure and a logit transformation of a standard life table survivorship function. The reciprocal of the proportion of the population of a particular age a, c(a), inflated by the exponentiated sum of population growth rates (adjusted if necessary for migration) up to age a, exp(R(a)), is linearly related to the logit of the standard survivorship function to age a, (1-p^s(a)) ps(a)). The intercept of the straight line is the reciprocal of the current birth rate, 1/b, and the slope is an indicator of the actual mortality level relative to that of the standard survivorship function, itself divided by the birth rate, (γ/b). Thus

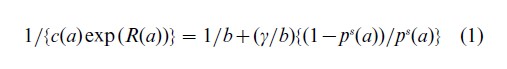
This method is an excellent example of how the mathematics of population age structures can be used to improve demographic estimation techniques.

The best-known and most widely applied indirect estimation method is the Brass (1964) method for estimating child mortality from women’s reports of the number of children born alive and the number that have died. It is argued that these reports, which involve no reporting of dates of events, are likely to be accurate in most populations, even those with substantial levels of illiteracy. The key indicator is the proportion dead of children ever born: the higher the level of child mortality, the higher the proportion dead, other things being equal. Brass’ contribution was devising a method to make other things equal. First, the data are classified by age of mother as a crude control for the average duration of exposure to risk of dying of a mother’s children. However, the age pattern of child-bearing still affects average exposure time. For women of a given age group, average exposure time of the children will be longer in an early childbearing population than in a late childbearing population. Brass used models of fertility and child mortality to evaluate adjustment factors k(i) for each five year age group of mother i needed to convert proportions dead PD(i) into life table probabilities of dying in childhood, _nq₀ , for a range of age locations of childbearing. In a particular application, the age location of childbearing was identified by the ratio of average parity for 15–19 year olds to that of 20–24 year olds, P(1)/P(2), and appropriate values of k(i) were obtained by interpolation from a standard table.

The original Brass method has undergone numerous refinements. Perhaps the most crucial development, however, was the insight by Feeney (1980) that under conditions of changing mortality, approximate reference dates could be put on estimates from different age groups of mother: the older the mothers, the further in the past the child mortality reflected by the survival of their children. Methods were developed not only to estimate levels of child mortality indirectly but also to estimate the recent time trend. Figure 1 shows the application of the method to data from the 1989 census of Kenya, together with direct estimates from the 1993 Kenya Demographic and Health Survey.

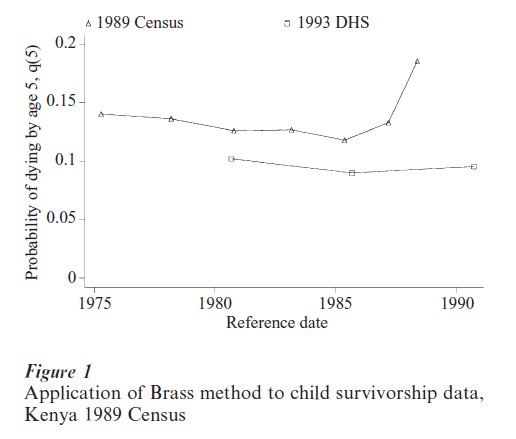
The Brass method and the developments of it have been very widely applied. It revolutionized knowledge of mortality conditions, particularly in sub-Saharan Africa but also in Latin America. It also gave rise to a concerted effort to find indirect estimation methods for adult mortality and migration. As such, it has proved one of the most influential ideas of demography.

The Previous Birth Technique is another indirect method for child mortality estimation. Where in-formation is available or can easily be collected concerning the survival of the birth immediately preceding a current delivery, the proportion dead among the preceding births can be calculated (Brass and Macrae 1984). The proportion dead turns out to be a good indicator of the probability of dying by age 2, ₂q₀ . Some information on average birth intervals permits refinement of this equivalence. The method is very easy to apply, but suffers from concerns about selection bias since reports are typically obtained from health facilities.

A number of indirect estimation methods have focused on adult mortality. One group relies on information on survival of close relatives. Adult survivorship can be estimated from information on survival of mothers or fathers (Brass and Hill 1973). The age of the respondent is the exposure time, the age distribution of parents at the time of the births of a group of respondents, the confounding variable that needs to be controlled. An ingenious approach to the estimation of maternal mortality has been the development of the Sisterhood method (Graham et al. 1989). Data are collected on survival of sisters with additional information for reported deaths about the timing of death relative to pregnancy. Despite the ingenuity of these approaches, questions remain about their accuracy.

A second group is made up of various forms of intercensal survival methods. Females aged 20–24 in 1990 will be aged 30–34 in 2000, so in the absence of net migration the ratio of females aged 30–34 in a 2000 census to females aged 20–24 in a 1990 census approximates the life table survivorship ratio ₅L₃₀/₅L₂₀ . Age distributional effects will be modest, but age misreporting and changes in census coverage can have large effects on such ratios, which as a result tend to be of little value in most developing countries. Generalized age structure equations involving age-specific growth rates have been used to minimize the effects of local age misreporting (Preston and Bennett 1983), but the method does not reduce effects of systematic age bias or coverage change.

The measurement of migration is problematic in many situations, because even sophisticated recording systems miss events. Net migration is often estimated as a residual from intercensal survival. In the example above, if the survivorship ratio ₅L₃₀/₅L₃₀ is known, a predicted number of females aged 30–34 in 2000 can be calculated by multiplying the number of 20–24 year olds in 1990 by this ratio. The difference between the observed and expected number of females aged 30–34 in 2000 is then an estimate of net intercensal migration by the 20–24 cohort. An alternative estimation procedure (Hill 1987) is available using the Demographic Balancing Equation: the change in size of an age group between two censuses is equal to the difference between intercensal entries (birthdays across the younger boundary of the age group plus in-migrants of the age group) and intercensal exits (birthdays across the upper boundary of the age group, deaths of the age group and out-migrants of the age group). Net migration can then be isolated and estimated from the other components. This latter approach has the advantage of producing estimates for age groups rather than cohorts. Both approaches, however, estimate migration as a residual, and are thus very sensitive to even quite small errors. Unlike most indirect estimation techniques, the indicator variable (change in population size) may be determined more by the confounder (mortality) than by the parameter of interest (migration). Results are therefore not robust.

Efforts have been made to estimate emigration from information on residence of relatives, particularly of children as reported by mothers and of siblings. These methods have not achieved widespread acceptance, however.

2. Consistency Checks

The best-known consistency check and adjustment technique is the Brass (1964) P F Ratio Method for fertility estimation. Records of births in a year by age of mother provide age-specific fertility rates. Information on children ever born by age of mother, provides measures of lifetime fertility. If fertility is not changing over time and the data are consistent, cumulated age-specific fertility to a particular age group will be the same as lifetime fertility or parity for that age group. Brass developed a simple way for cumulating current age-specific fertility rates to approximate parity equivalents (F (i)) in order to check consistency with parities (P (i)) for each age group i. However, he also went further, to hypothesize that typical errors in records of numbers of births might be proportionately constant by age of mother, so that the age-specific fertility rates would have the correct shape, but at a potentially incorrect level. Typical errors of reporting of children ever born, however, were hypothesized to vary by age, but to be smallest for younger women. Ratios of P: F for successive age groups, thus not only reflect consistency but, for younger women, represent potential adjustment factors for the age-specific fertility rates.

The assumption of unchanging fertility can be relaxed if information is available on average parity for two points in time (Zlotnik and Hill 1981). Parity changes by cohort between the two sources can then be cumulated to obtain a period-specific parity distribution that can be compared with cumulated period-specific fertility rates. If the other assumptions hold, adjustment can be made even under conditions of changing fertility.

Consistency checks with the option for adjustment in the measurement of adult mortality have largely focused on comparisons of the age distribution of deaths with the age distribution of the population. The first such method was proposed by Brass (1975). In any population with negligible migration, the entry rate into any open-ended age segment a+ is equal to the growth rate of the segment plus the death rate in the segment. In a stable population, the growth rate r is constant at all ages, so if b(a+ ) is the entry rate and d(a+) is the exit rate,

If deaths are recorded with a completeness c (assumed constant at all adult ages) relative to the population, the recording of which is also assumed to be of constant completeness at all ages, and b(a + ) is estimated from the population age distribution alone,

where d ^o(a+) is the observed death rate over age a. There is thus a linear relationship between the entry rate and the observed death rate, the intercept of which is the stable growth rate and the slope of which is the reciprocal of the completeness of death registration.

The assumption of stability can be relaxed if two successive population counts are available and growth rates over ages a can be measured directly (Hill 1987). If census coverage is constant within, but not between, the censuses,

where r^o(a + ) is the observed growth rate over age a and k is the natural log of the change in coverage from the first to the second census. Figure 2 shows the application of both growth balance methods to Chinese census data for females, using the 1990 age distribution and deaths by age for the stable version, and 1982 to 1990 population change together with the distribution of deaths by age for the general version. The improved smoothness of the general version for this destabilized population is evident.

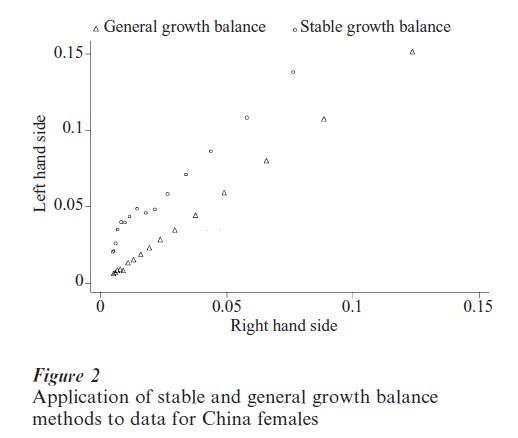
Other equations for population age structure can also be used as the basis for similar consistency checks. In an influential paper, Bennett and Horiuchi (1981) use the exponentiated sum of age specific growth rates above age a to expand the deaths at each age to equate deaths above age a to population age a. Though error patterns are likely to affect these methods in slightly different ways, there is no consensus as to which should be preferred in different situations.

3. Future Directions

Indirect estimation is an interim solution to data problems. Data quality will improve, rendering these techniques unnecessary. Birth histories have shown that reasonably accurate direct estimates of fertility and child mortality can be obtained by survey methods. However, for the foreseeable future, indirect estimates of child mortality based on census data will remain the only viable approach to studying small-area differentials in many parts of the world, and indirect estimates of adult mortality and migration still remain important approaches even at the national level.

Bibliography:

1. Bennett N, Horiuchi S 1981 Estimating the completeness of death registration in a closed population. Population Index 47(2): 207–21
2. Brass W 1964 Uses of census or survey data for the estimation of vital rates. Paper prepared for the African Seminar on Vital Statistics, Addis Ababa, 14–19 December 1964
3. Brass W 1975 Methods for Estimating Fertility and Mortality from Limited and Defective Data. Occasional Publication of the Laboratory for Population Statistics. University of North Carolina, Chapel Hill, NC
4. Brass W, Hill K 1973 Estimating adult mortality from orphanhood. Proceedings of the International Population Conference, Liege. IUSSP, Liege, Belgium
5. Brass W, Macrae S 1984 Childhood mortality estimates from reports on previous births given by mothers at the time of a maternity. Asian and Pacific Census Forum 11(2): 5–8
6. Cho L-J, Retherford R, Choe M 1986 The ‘Own Children’ Method of Fertility Estimation. East-West Center, Honolulu, HI
7. Feeney G 1980 Estimating mortality trends from child survivorship data: A demographic approach. Population Studies 34(1): 109–28
8. Graham W, Brass W, Snow R 1989 Estimating maternal mortality: The sisterhood method. Studies in Family Planning 20(3): 125–35
9. Hill K 1987 Estimating census and death registration completeness. Asian and Pacific Population Forum 1(3): 8–13
10. Preston S 1983 An integrated system for demographic estimation from two age distributions. Demography 20(2): 213–26
11. Preston S, Bennett N 1983 A census-based method for estimating adult mortality. Population Studies 37(1): 91–104
12. United Nations 1983 Manual X: Indirect Techniques for Demo-graphic Estimation. United Nations, New York
13. Zlotnik H, Hill K 1981 The use of hypothetical cohorts in estimating demographic parameters under conditions of changing fertility and mortality. Demography 18(1): 103–22