Demographic Measurement And Measures Of Fertility Research Paper

Events can be thought of as changes in state and, correspondingly, states can be considered to result from the occurrence and nonoccurrence of events. For example, the event of first marriage changes a person’s marital status from single to married, and a person who has married and has not yet experienced the dissolution of their marriage is in the state of being currently married. In addition, the concepts of ‘cumulative experience’ and ‘state’ are to some extent interchangeable, for example, a woman who has had n live births (cumulated experience) is said to be of parity n (state). Measures of cumulative experience that do not refer to individual states are also used in demography, and these will be considered presently. The current entry does not deal with methods of collecting and classifying demographic data, but with the use of data once it has been collected and processed, ready for analysis.

Demography is concerned in general with aggregate phenomena at the population level, where populations vary from global to local in extent. The units whose events and states are aggregated can be individuals, couples, families, or households. Some demographic measures are, however, strictly aggregate in type, for example, a population growth rate, population density per unit area, or a population dependency ratio all have meaning at the aggregate level only. Demo-graphic measures focus on level, timing, and distribution: the frequency of events or prevalence of states (level), the age at or time between events (timing), and distributional aspects such as age structure.

The need for demographic rates and other measures is readily stated. Absolute numbers, whether population size or numbers of vital events, are certainly of demographic interest, particularly in an applied con-text, and are frequently the key input or output for policy purposes. However, population analysis is conducted in terms of the underlying phenomena— mortality, fertility, migration, and so on—that determine population change. For example, population projections are usually carried out by the component method, applying assumptions about fertility, mortality, and migration rates, rather than by extrapolating birth, death, or population numbers using mathematical models. Rates, proportions, and other indices are required also for comparative purposes, whether tracking time trends or making comparisons between (sub)populations. Spatially and temporally, populations vary in size and also in structure, and so measures that abstract from size and structure are required to compare the demographic metabolism, so to speak, of different populations.

Demographic rates and measures are numerous. The variety stems both from the widely varying forms in which data are available and from the nature of the phenomena themselves. Data may come from vital registration systems, from censuses and surveys, from parish registers, or from administrative records. These sources may differ in the kinds of information recorded, in questions asked, and in details published. Fertility is the area in which measures are probably most numerous, a result of the complexity of the phenomenon: births are repeatable events, they can occur to women inside and outside of marital or cohabiting unions, their order in a birth history can be of significance, and they can be associated with several dimensions of personal time—age, union duration, duration since previous birth, and so on.

1.2 Rates, Probabilities, Proportions, And Ratios

A demographic rate expresses the number of events occurring relative to person years at risk of the event in a defined population for a specified time and place. It may be expressed per person year, per 1,000 person years, per 100,000 person years at risk, and so on. The denominator, person years at risk, is often estimated by means of the mid-year population or by the average of two end-year population figures, each of these being an approximation to the average population during the year. Francophone demographers distinguish between type 1 rates (taux de premiere categorie), in which the denominator of a rate is confined to those who have not yet experienced the event in question, and type 2 rates, where no such restriction is made (taux de deuxieme categorie). No special terminology is commonly accepted for this purpose in English-language demography, the distinction between such rates being implicit in the specification of the rate, but the English version of the French terminology will be used occasionally for brevity and precision. A probability is the likelihood that an individual will experience an event. It is estimated by the number of events occurring during a defined period or at a particular age to a specified group divided by the numbers of individuals present at the start of the period or age. A proportion is defined in the usual way, as the number with a given attribute at a given time point divided by the total population in question at that time. Finally, demographic measures also take the form of ratios, for example, the sex ratio at birth is the ratio of the numbers of male to female births. Ratios generally refer to aggregates, although anthropometric measurements in ratio form relating to individuals are also found in the medical demographic literature.

1.3 Crude Rates And Degree Of Specificity

Demographic measures vary in their level of detail. The simplest are crude rates, expressed as the number of events per 1,000 (or other multiple) of the total population, without any further specificity. The two most common are the crude birth rate (CBR)—the number of births per 1,000 population in a year—and the crude death rate (CDR)—the number of deaths per 1,000 population in a year. They give basic information but do not allow refined analysis. Crude rates are of value in setting out the basic demographic parameters of a population and are used for descriptive purposes, for instance, when data needed for more detailed measures are either unavailable or unreliable.

Demographic rates and other measures are influenced by the composition of the numerator in respect of any factor by which the frequency of the phenomenon under study varies. Most importantly, crude rates are influenced by the age structure of a population, because of the pervasive association between age and demographic event rates, and also by sex composition, since demographic event rates usually vary by sex. Accordingly, specific rates may be calculated by restricting the numerator or the de-nominator, or both. Specificity may be introduced for one or more factors. For example, age-specific rates may be influenced by composition in respect of marital status, duration in a particular state, parity (number of children already born to a woman), urban rural residence, and so on. So, the analyst might choose to calculate rates specific for a number of dimensions. For some purposes, variation according to specific factors may itself be the focus of interest. In other contexts, variation with respect to, for example, age is taken as given and is not the subject of study. If so, the analyst will wish to remove the compositional effect from the comparison to be made. Traditionally, one of two procedures is used to remove the influence of such (nuisance) factors. Rates may standardized for the factors concerned or may be disaggregated progressively so as to arrive at rates specific for groups with greater (or in theory perhaps complete) internal homogeneity. Standardization may be through the conventional direct or indirect methods or by calculating a synthetic indicator of some kind (see Sect. 2.1.3 below).

Both procedures have disadvantages. Standardization, whether by the conventional direct or indirect methods, or by constructing synthetic indicators, is well known to be valid only where there are no interactions between the factors for which the standardization is carried out, or when there are no interactions between them and the categories, populations, etc. to be compared. Since such interactions are often found, straightforward standardization is inappropriate in many instances. Progressive disaggregation of rates has the disadvantage of producing potentially large numbers of rates that are not readily summarized and perhaps not readily interpretable. Modern methods of model fitting can in many instances provide a more general and rigorous solution to the pervasive need for standardization in demo-graphic analysis, and can offer a considerable advance on the progressive disaggregation approach. Hoem (1987) and his predecessors have shown that indirect standardization can be seen as a first step in an iterative estimation procedure for intensity regression based on a multiplicative hazard model.

2. Measures Of Fertility

2.1 Level

2.1.1 Crude And Specific Rates. The definition of the most common fertility measures is set out in Table 1. The CBR is widely used in cross-national comparison, particularly since the data required (an estimate of total births and of total population) are generally available. The general fertility rate (GFR) is more specific, in that it restricts the denominator to those at risk of experiencing a birth, that is, women of childbearing age (most commonly taken as ages 15–44). Age-specific fertility rates (ASFRs) intro-duce a further level of detail by age and have importance both in indicating the pattern of childbearing by age and as the basis for calculating the total fertility rate (see below). Age-specific fertility rates may be disaggregated further to obtain age-specific marital fertility rates and age-specific nonmarital fertility rates. Fertility rates may also be calculated specific for duration of partnership or marriage, in place of or jointly with age.

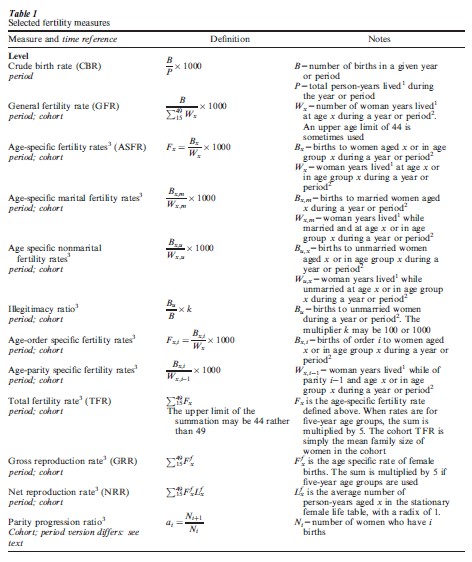
In the last few decades, fertility rates that are specific by order of birth have come into prominence. Such rates are particularly informative since time trends may vary by order of birth, particularly in modern contracepting populations or in populations where the use of contraception is on the increase. They are of two distinct types. Less detailed are rates in which the numerator only is disaggregated by order of birth, giving, for example, age-order-specific fertility rates. These are demographic rates of type 2, since the denominator includes all women of a given age, although the numerator is specific by order of birth. They should be distinguished from the more detailed age-parity-specific fertility rates in which the numerator consists of births of order i to women aged x and the numerator of women of parity i–1 who are aged x. (These latter are rates of type 1; note that the term ‘order’ relates to births and that ‘parity’ relates to women.) In the case of first births, both order-specific and parity-specific rates may also be specific by duration since marriage (or start of union), either in place of or combined with age-specificity; for second and higher order births, correspondingly, duration since previous birth may be specified in place of or in addition to age. Computing measures of fertility that are specific by order of birth from vital registration data can present data problems because the order of birth as recorded in a particular system may exclude a woman’s premarital births and/or births occurring in previous marriages, and so may not represent true birth order over the woman’s entire childbearing history.

With the exception of the crude birth rate, which applies only to a time period, all of these fertility rates may be calculated either on a calendar-period or cohort basis.

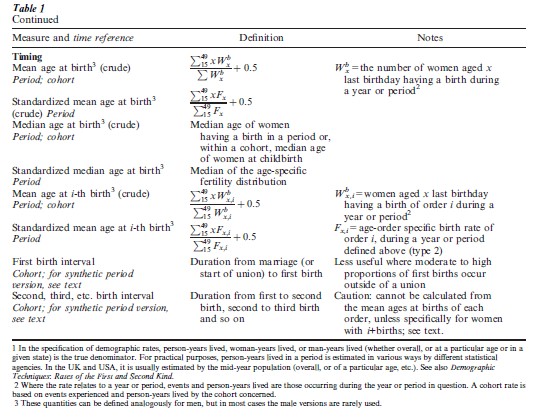
2.1.2 Parity Progression Ratios. Fertility rates may vary by parity, and in modern contracepting populations always do so. Because any given overall level of fertility may be reached through differing patterns of parity-specific birth rates, measures known as parity progression ratios (PPRs) were developed in the early 1950s to summarize the lifetime outcome of such variation. The parity progression ratio of order i is defined as the proportion of women of final parity i and above who, by the end of childbearing, have had at least i+1 births. Here i=0, 1, 2 … m–1, where m is the maximum number of births to any woman in the population. These ratios express, in other words, the probability that a woman who has had a given number of live births will have at least one further birth. In their original form, parity progression ratios are calculated on a cohort basis, al-though they are meaningful for any group of women aged 45 plus. Methods for estimating these for women who have not reached the end of childbearing have also been proposed (Brass and Juarez 1983).

2.1.3 Synthetic Or Hypothetical Cohort Indicators. Since there are many specific fertility rates of any particular type, it is convenient, indeed a practical necessity, to have single-figure indices that summarize them. Such indices are also of value in producing estimates of lifetime experience on the basis of a single period’s data, both because cohort data are often not available and because cohort data rep-resent cumulative past rather than current experience. Synthetic or hypothetical cohort indicators are used for this purpose. A synthetic summary indicator is obtained by combining the specific rates of a calendar period to obtain an overall figure representing the lifetime fertility outcome that would result if a cohort of women experienced the period rates in question throughout their childbearing years. The component rates are combined in one of two ways: either multiplicatively, as in a life table, or by adding the age-specific rates at each age. In the first type of procedure, the denominators include only ‘survivors,’ that is those who have not yet experienced the event by the age or duration in question (rates probabilities of type 1). The second type of procedure is used when the denominator of each age-specific rate includes both those who have and those who have not yet experienced the event (rates of type 2). The exact details depend on the type of rate in question and are mentioned below in each case.

The most widely used such summary indicator in the fertility arena is the classic period total fertility rate (TFR), obtained by adding the age-specific fertility rates (i.e., type 2 rates) of a given year or period across ages 15 to 44 or 15 to 49. The result can be interpreted as the average number of children that women would bear, if they were to experience throughout their childbearing years the age-specific rates of the period in question. (For a modern underpinning of this classical interpretation, see Borgan and Hoem 1988.) It can also be seen as the average number of children per woman if the age-specific rates in question were to remain in force over a long period. Closely related to the classic total fertility rate are the gross reproduction rate (GRR) and the net reproduction rate (NRR). The GRR is simply the TFR confined to female births, and so represents the average number of daughters a woman would have if she experienced the age-specific female birth rates of a particular period. The NRR is obtained by modifying the GRR to take account of the probability that a newborn female may die before reaching reproductive age (see Table 1); it represents thus the average number of daughters who would reach reproductive age per woman of reproductive age that would result if a period’s age-specific female fertility and mortality rates were to remain fixed. In a stable population, in which vital rates are and have been fixed over a lengthy period, the NRR represents the extent to which generations replace themselves. In these circumstances an NRR of <1, =1, or >1 means that successive generations are, respectively, declining, stationary, or growing in numerical size, and so that overall population numbers are changing correspondingly. The GRR is roughly half the size of the TFR; the NRR is less than the GRR, with the gap between them depending on the level of female mortality at ages under 45 or 50: the higher the mortality level, the greater the disparity between the GRR and the NRR. The TFR, GRR, and NRR can also be specified on a male basis, that is using male age-specific fertility rates, and male survivorship, and the results will in general differ from the female values. Female rates being more widely available and more reliable, they are in general preferred to male rates.

An advantage of the TFR, the GRR, and the NRR is that they are standardized for age, the standard population being one imaginary woman proceeding through 30 or 35 years of childbearing. Synthetic or hypothetical cohort indicators in general—whether of fertility, nuptiality, mortality, and so on—can be criticized for the fact that they express period events in a metric of lifetime experience, and that this is conceptually at variance with the usually short period of calendar time whose demographic processes they represent (Nı Bhrolchain 1992). Two points can be made in answer to this difficulty. First, the discrepancy between time series of summary cohort indicators and corresponding period synthetic summary indicators such as the TFR is well known, and the origins of the discrepancies between them have been widely discussed. Second, synthetic indicators can be thought of simply as convenient statistical summaries of the specific rates obtaining in a particular period—as a rough summary of the overall level of a phenomenon.

The major and well known source of discrepancy between cohort and period time series of the TFR, originally identified by Hajnal (1947) in relation to the GRR and NRR, is that time trends in the period TFR are influenced not only by the level of fertility but also by changes in the timing of childbearing. Where successive cohorts are moving to an earlier pattern of childbearing, the period TFR will be inflated, and where cohort fertility is slowing in pace the period TFR will be deflated, relative to the cohort series.

A related source of inaccuracy in these summary measures is that the additive (although not the multiplicative) method of combining a period’s rates takes no account of past experience, at earlier ages or durations, of that event, particularly in the case of fertility. Past experience of events is likely to influence current type 2 rates, for example, if proportionately more of a given age group have already had a first birth, the (type 2) age-specific first birth rates can be expected to be lower than if proportionately fewer of the group have already begun childbearing. Further-more, in a population where age-specific rates vary from year to year—almost always the case in real situations—the past experience of age groups in successive calendar periods (or, equivalently, successive cohorts) will differ. Thus, any additive summary indicator will be influenced by the composition of each age group with respect to past experience.

A final difficulty is that additive synthetic indicators may sometimes produce results that are impossible if the summary is interpreted as relating to a real cohort: for example, the sum of period age-specific first birth rates may exceed one, which appears to imply more than one first birth per woman. This last weakness is not present in multiplicative summary indices.

One solution to the difficulties inherent in the classic TFR is to use cohort fertility series to supplement period information. Hajnal (1947) suggested that the fertility experience of successive cohorts be deployed to reflect long-run trends, and that period fertility be employed to reflect recent and current trends, a practice that has become firmly established in demo-graphic analysis since that time. Another alternative has become available more recently: synthetic or hypothetical cohort indicators calculated on a multiplicative basis. Such measures correct in part for differences in composition resulting from past experience, and have the advantage also that they do not produce results that would be impossible in a true cohort. The best known of these in current use in the fertility arena is the period parity progression ratio (PPPR), devised originally by Henry (1953). PPPRs are constructed from the parity-and age-and/or duration-specific probabilities obtaining in a period, yielding one summary indicator of the level of progression to each order of birth in a period. The (type 1) probabilities at each age or duration are essentially assembled as a life table, with age or duration as the measure of elapsed time, and the proportion having experienced the event (i.e., not ‘surviving’) by some specified age or duration estimated in the conventional way. This proportion represents the parity progression ratio that would result if a cohort were to experience during their lifetime the parity-and age-and/or duration-specific birth probabilities of a particular period. For the specification of these indices see Feeney and Yu (1987), Nı Bhrolchain (1987), and Rallu and Toulemon (1994). The PPPRs can be used to obtain an estimate of the period TFR that is alternative to the standard TFR, generated as

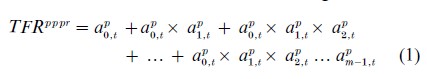
where a^p_i, is the period parity progression ratio of order i for period t, and m is the maximum number of births occurring. (A standard notation is not yet in use for these quantities.)

This version of the TFR has the advantage over the conventional (additive) TFR that its components, the PPPRs, standardize to some extent for past experience and remove part of the timing influence, but it shares with the classic TFR the weakness that a single-figure summary may conceal parity-, age-, or duration- specific variation in probabilities that go beyond pure differences of level.

The issue of how best to summarize specific birth rates to obtain period time series is the subject of current research and debate (Nı Bhrolchain 1992, Bongaarts and Feeney 1998). The classic TFR is recognized as too crude in many instances, and period parity progression ratios have been accepted as offering considerable clarification, especially in low- fertility societies and in societies in the course of fertility decline. One question at issue is to identify correctly the precise nature of time trends or cross- national differences, so that explanatory inquiry can be accurately focused on these, rather than on a potentially misleading summary indicator. Another objective is to make the best use of existing information in order to evaluate past and likely future trends. Further developments may be anticipated in this area in coming years.

2.2 Timing

Measures of fertility timing are somewhat less numerous than indicators of fertility level. The mean and median age at birth are the most basic ones. Somewhat more precise is the mean or median age specific by order of birth: mean or median age at first birth, at second birth, and so on. Mean and median ages may be obtained from either period or cohort data, and as with measures of the level of fertility, time series of these will generally differ. Whether or not specific by order, the period mean or median age at birth can be calculated in crude or standardized form, and published sources do not always indicate which of these is presented. The period crude mean age at birth (or at first birth, second birth, etc.) is obtained simply as the arithmetic mean age of all women having a (first, second, etc.) birth in a given period. The crude mean age at birth is widely used but has the disadvantage, in a period context, of being influenced by the age structure of women of childbearing age, which can vary through time and especially from one country to another. Far better for the purposes of period analysis, although more demanding of data since population denominators are required, is the standardized mean age at birth, or at first birth, second birth, and so on. Standardization is unnecessary in a cohort framework, which is self-standardizing, although care should be taken in comparisons of cohorts widely differing in mortality during the childbearing years. The standardized mean age at birth is obtained by weighting by the relative period age-specific fertility rates at each age (see Table 1) and so is, in fact, the mean of the age-specific fertility distribution. Similarly, the standardized mean age at i-th birth uses as weights the relative age-order-specific fertility rates (type 2, not type 1 rates; see above). The standardized mean age at birth is not a pure measure of fertility timing since it is influenced by the overall level of fertility. Two populations could have identical (standardized) mean ages at births of each order but the standardized mean age at birth could be later in one than in the other because proportionately more women in the first population go on to have births of higher orders. A measure of fertility timing encountered mostly in the historical demographic literature, the mean age at last birth, is used as an indirect indicator of the presence of birth control. This measure can be calculated without bias only for women who have reached the end of re-production (age 45 or 50).

Another set of indicators of fertility tempo is the mean or median duration of birth intervals. The first birth interval is the time from marriage (or start of informal union) to the first birth. (This interval may be of limited value where a large proportion of births occur outside of formal or informal marital unions.) Later intervals are obtained as the duration from first to second birth (second birth interval), from second to third birth (third birth interval), and so on. Birth intervals calculated from the ages of a group of women at births of successive orders are incorrect because the ages at successively higher orders of birth are based on women of differing ultimate family sizes. The problem is that women who at the end of childbearing have larger families are usually younger at births of any given order than are those with smaller completed families. The i-th birth interval is calculated instead as (a) the time from birth i-1 (or start of union when i=1) to birth i among women with i or more births, or equivalently as (b) the age at birth i minus the age at birth i-1 (or start of union when i =1) among women with i or more births. Where individual level data are available, means or medians may then be calculated. If aggregate data only are available, median intervals cannot be calculated accurately by differencing successive median ages at birth within parity groups. The median may be preferred to the mean birth interval, since birth interval distributions are typically positively skewed. Synthetic or hypothetical mean or median birth intervals for time periods may be obtained from the life tables used in constructing PPPRs, thus giving a period measure of birth timing analogous to, and supplementing, the standardized mean age at birth (Nı Bhrolchain 1987).

Of importance in stable population theory is the mean length of a generation, which is the time it takes a stable population to grow by the factor NRR. It is represented in stable population theory by the symbol T and is given by T=(ln NRR)/r, where r is the intrinsic growth rate of a stable population.

Bibliography:

1. Bongaarts J, Feeney G 1998 On the quantum and tempo of fertility. Population and Development Review 24: 271–91
2. Borgan O, Hoem J M 1988 Demographic reproduction rates and the estimation of an expected total count per person in an open population. Journal of the American Statistical Association 83: 886–91
3. Brass W, Juarez F 1983 Censored parity progression ratios from birth histories. Asia and Pacific Census Forum 10: 5–13
4. Feeney G, Yu J-Y 1987 Period parity progression measures of fertility in China. Population Studies 41: 77–102
5. Henry L 1953 Fecondite des mariages. Nou elle methode de mesure. INED, Paris (English translation 1980 Fertility of Marriage: A New Method of Measurement. UN ESCAP Population Translation Series No. 3)
6. Hoem J M 1987 Statistical analysis of a multiplicative model and its application to the standardization of vital rates: A review. International Statistical Review 55: 119–52
7. Nı Bhrolchain M 1987 Period parity progression ratios and birth intervals in England and Wales, 1941–1971. Population Studies 41: 103–25
8. Nı Bhrolchain M 1992 Period paramount? A critique of the cohort approach to fertility. Population and Development Review 18: 599–629
9. Preston S, Heuveline P, Guillot M 2000 Demography. Measuring and Modelling Population Processes. Oxford University Press, Oxford, UK
10. Rallu J-L, Toulemon L 1994 Period fertility measures: The construction of different indices and their application to France, 1946–89. Population (An English Selection) 6: 59–93
11. Shryock H S, Siegel J S 1976 The Methods and Materials of Demography. Condensed Version. Academic Press, New York