Sample Classical Applications Of Stable Population Theory Research Paper. Browse other research paper examples and check the list of research paper topics for more inspiration. iResearchNet offers academic assignment help for students all over the world: writing from scratch, editing, proofreading, problem solving, from essays to dissertations, from humanities to STEM. We offer full confidentiality, safe payment, originality, and money-back guarantee. Secure your academic success with our risk-free services.
1. Introduction
Virtually any real population, whether contemporary or historical, deviates from stability, but the stable model produces a standard for comparison based on simplifying assumptions that allow us to handle data limitations. This research paper will review several applications within a structure that specifies the amount of information that is required. The applications are ‘classical’ in the sense that they are relatively well known.
Academic Writing, Editing, Proofreading, And Problem Solving Services
Get 10% OFF with 24START discount code
It is helpful first to distinguish between two classes of models that are widely used: survival processes and renewal processes. The prototypical example of a survival process is the single-sex, single-decrement life table. A survival process describes a cohort, real or synthetic, from age 0 until some terminal age ω. The main concepts are (a) the survival function, l(x), namely the proportion of the cohort that survives to each age x, and (b)o the mean waiting time or remaining life expectancy, ex, at any specific age x.
A renewal process, by contrast, is a survival process with reproduction. With this component, the process generates successive cohorts that are (in general) larger than necessary simply to replace the persons who have died. The cohort interpretation is supplemented with the asymptotic implications of fixed and stable overall rates (of growth, mortality, and fertility), and a fixed and stable age distribution, none of which depends on initial conditions.
If a renewal process is in equilibrium—that is, if reproduction is exactly at replacement value, then the stable population is stationary. It has an intrinsic growth rate of zero, and one does not need explicit age-specific birth rates to analyze it, for its overall birth rate is identical to the overall death rate. There are several classical applications and generalizations of this scenario, all of which can be regarded as applications of stable population theory because a survival process is a special stable renewal process.
A stable population is typically motivated as the asymptotic consequence of projecting the population indefinitely with fixed age-specific rates. Its overall rates and age distribution converge to functions that do not depend on the initial conditions. However, unless the intrinsic growth rate is zero, there is a fundamental implausibility in this asymptotic interpretation. If the intrinsic growth rate is positive, then the overall population size will increase exponentially, an outcome that cannot be sustained indefinitely in a real population. If the intrinsic growth rate is negative, then the overall population size will decrease exponentially until eventual extinction. In probabilistic terms, the fixed-rates assumption implies almost certain ultimate extinction or explosion. It is probably more useful to regard the stable population parameters simply as a synthesis of the underlying age-specific probabilities or rates.
2. Applications Not Requiring Schedules Of Rates
Applications of stable population assumptions can be organized according to the amount of information they utilize. Probably the simplest possible applications occur when the only parameter utilized is the intrinsic growth rate, r. If we assume stability between two times t1 and t2, and that the population size at those two times is n1 and n2 , then
![]()
Solving for r, we get
![]()
We can then estimate the population size at an intermediate time, t1 ≤ t ≤t2 , to be n1er(t-t1). This formula, or variations upon it, is often used when the population is not stable, in the absence of better information. Another simple and well-known application is to determine the doubling time associated with a given value of r. Setting n2 =2n1 and letting T be the time required for the population to double, we obtain 2n1 =n1erT, leading to T = (ln 2)/r = 0.6931/r. For example, if the annual growth rate is 0.01, or 1 percent, a stable population will double in 69.31 years, or approximately seventy years. These and related applications are discussed by Hinde (1998, pp. 154–8), for example.
Suppose that in addition to the intrinsic growth rate, r, we also know the intrinsic birth rate, b (and hence the intrinsic death rate d = b – r). Keyfitz (1977, pp. 12–14) uses such information to estimate the number of persons who have ever lived on Earth, which is the same as the number of persons ever born. His strategy is to piece together long intervals of time within which stability (at different levels) is assumed. If the population is stable between t1 and t2, then the number of person-years lived in that time interval will be
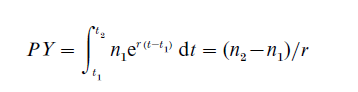
PY can be converted to the corresponding number of births by multiplying by b:
![]()
3. Applications That Assume Schedules Of Rates
Another class of applications arises if we know r, b, and d, and do not know the survival and fertility schedules but are willing to make some assumptions about them. Coale and Demeny (1983) blended empirical life tables into four sets of so-called regional model life tables (north, south, east, and west) o for males and females, keyed to the life expectancy eo0 at birth and eo10 at age 10. They also developed plausible fertility schedules, varying according to the mean age of childbearing but adding up to one child, so that the entire schedule could be multiplied by a hypothetical total fertility rate (TFR). With this information, much of it hypothetical, they were able to generate sets of stable age distributions. It is then possible to estimate a wide range of population characteristics, using only a few pieces of summary information (along with a specification of region and sex). The summary information typically includes certain combinations of the following: a measure of growth, such as r; a measure of fertility, such as b, the gross reproduction rate (GRR), or the TFR; a measure of mortality, such as d or the average age at death; or a measure of the age distribution, such as the proportion of persons below age 20. Stable age distributions generated in this way can also be used to approximate real age distributions in settings of deficient data. Some methods for the computation of population parameters using the stable population model are described in Demographic Techniques: Indirect Estimation.
4. Applications That Require Schedules Of Rates
A number of analyses of population dynamics have resulted from examining the sensitivity of population characteristics to disturbances of a stable population. These applications require knowledge of the agespecific schedules for mortality (say mx for each age x), of fertility (say fx for each x), and for any other transitions in the model. For example, Preston (1974) took partial derivatives of the basic stable population formulas to estimate the effect of various age-specific mortality changes upon the intrinsic growth rate, birth rate, and age composition. He found that the effects could be represented as simple functions of the age pattern of the cumulative changes in the mortality rates. Probably the best known of these sensitivity analyses has been on the topic of population momentum, which in its simplest form measures the eventual effect on population growth of an immediate shift to replacement fertility.
The classical stable population model has no in-or out-migration, but several authors have used the model in innovative ways to evaluate the impact of emigration (Keyfitz 1971) or immigration (Lesthaeghe et al. 1988). Mitra (1990) considered how a population could maintain stationarity through a combination of below-replacement fertility and a steady stream of immigration. With assumptions about the ages and fertility of the immigrants, it is possible to determine the necessary size of the stream of immigration. This model is relevant, at least as a first approximation, to the current mix of below-replacement fertility and immigration in Europe and North America.
The classical formulation of stable population theory only allows individuals to be born, procreate, and die, but later developments permit individuals to move between several statuses or states during their lifetime, as in multistate models. In one obvious application the states represent regions of a territory (Feeney 1970). In another, Keyfitz developed a linkage between aging and career mobility in stable populations (1973; the title of this paper is misleading because he included stable as well as stationary populations). He supposed that advancement in status across a set of discrete categories is essentially based on the steepness of the age distribution. In a setting of high growth, age (as a proxy for experience) tends to produce earlier advancement because there are relatively few people at higher levels. In a setting of low growth, seniority is less valued, because there are relatively many people at higher levels, and promotion will take longer. The approach is again a type of sensitivity analysis, in which the age at reaching a sequence of discrete gateways is expressed as a function of stable population parameters (in particular, the intrinsic growth rate).
5. Applications That Link Individuals To One Another: Kinship
Assume now that we have access to complete schedules of survival and fertility. In continuous form, say that l(x) is the probability that a woman will survive to age x and m (x) dx is the probability that a woman will have a daughter between ages x and x + dx (with m (x) > 0 for x in the reproductive age range α < x < β within the full range of ages 0 < x < ω).
Single-sex kinship provides a structure by which individuals are linked through lines of descent or ancestry. Two specific models for kinship structures will be described here. In the context of kinship, reference individuals (ego) are linked to their direct descendants, such as daughters; to progenitors, such as mothers; or to their lateral kin, such as sisters. Twosex approximations are possible. The main outputs are the probability that a specific progenitor is still alive when ego is age a, and the expected number of descendants and lateral kin (in a specific category) who are still alive, or were ever born, when ego is age a. These are obtained from various convolutions of the survival and fertility functions.
The first kinship model to be described was developed by Goodman et al. (1974, 1975). The following exposition will be limited to surviving kin when ego is age a. It can be modified to refer to kin ever born simply by deletion of the outermost survival function (that is, setting it equal to 1).
Each kinship role is expressed with a different formula, but the strategy for generating these formulas is the same for all roles. The steps to link ego with a consanguineal relative are to identify the relevant sequence of births, and the ages of the respective mothers at those dates; to incorporate the fertility rates for those ages, the probability of surviving to those ages, and, for the final link, the probability of surviving to the time when ego is age a; and integrating over all allowable combinations of ages of the linked kin. Note that the birth of ego herself, and her survival to age a, are assumed.
For example, to link ego with her daughter, the relevant birth is that of the daughter, which occurred when ego was some previous age x. If the daughter is still alive when ego is age a, then the daughter’s age is a – x. Thus ego experienced the fertility rate for age x, and the daughter survived to age a – x. Multiplying in reverse order and integrating over allowable ages x, the expected number of surviving daughters for a woman age a is
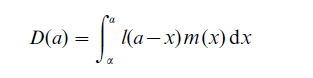
(If a < α then D(a) = 0 and if a > β then D(a) = D ( β).)
The stable population probability that ego’s mother is alive when ego is age a was originally calculated by Lotka (1931), and is useful for estimating adult mortality when some empirical information about the incidence of orphanhood is available. If the mother was age x when ego was born, then the probability that she is still alive a years later is the probability of surviving to age a + x, l (a + x)/l (x). Obviously this depends on the value of x, as well as a, and these survival ratios must be weighted by the probability that the mother was age x to age x + dx when ego was born. In a stable population these weights will be given by W (x)dx = e−rxl (x) m(x)dx (from the characteristic equation, this is the density function for mothers’ ages and integrates to 1). Therefore,
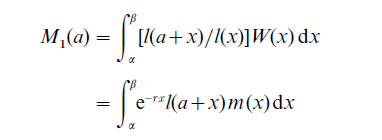
is the probability that ego’s mother is alive when ego is age a.
The expected number of surviving sisters when ego is age a involves a similar logic but will not be given here. Ego is linked to her sisters through their mother. It is necessary to distinguish between older and younger sisters because the survivorship of the mother is problematic after, although not before, the birth of ego. The formulas can be extended to aunts, nieces, first cousins (mother’s sister’s daughters), and indeed any category of kin.
A noteworthy feature of this application of the basic model of a stable population is that it requires only the basic survival function and maternity function, and a structure to link individuals. As an alternative to linkage by kinship, it should be possible to substitute an organizational structure or some form of vertical and horizontal connections, but we are not aware of any analogous applications.
The formulas are deterministic, rather than stochastic, and will not produce distributions. They assume that the birth of a child is independent of the number of children a woman has already had, that survivorship is independent of biological relationship, and that the population is homogeneous. Although these limitations are severe, it would be difficult to find data corresponding to more realistic assumptions. Calculations using these multiple integrals require some form of quadrature.
In a second application of kinship (Pullum 1982), counts are not conditional upon the survival of ego or any other kin, but are defined as ‘eventual expected’ numbers of kin. For example, the net reproduction rate
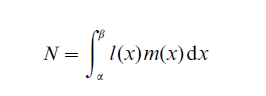
is the average number of female births that will be produced, a generation later, from a single female birth. This is equivalent to the eventual expected number of daughters that a woman (ego) will have, defined at the point of ego’s birth and the daughters’ births.
The eventual expected number of sisters, defined at the point of ego’s births and the daughters’ births, can be referred to with the symbol S. N is not equivalent to any of the functions defined by Goodman et al. (1974) but S does appear within their scheme as the (expected) number of sisters (older and younger added together) ever born by the time ego has reached age β – α, the maximum age at which a sister can be born. This formula superfluously conditions on the survival of ego, but allows for all sisters to be born.
It can be shown that N and S are sufficient to obtain the eventual expected numbers of any other types of kin. For example, an average of N2 granddaughters (daughters of daughters) will be born, SN first cousins (daughters of sisters of the mother), SN nieces (daughters of sisters), and so on. The sex ratio at birth will also be constant in a stable population, and by including it one can easily extend to a two-sex kinship structure. For example, define s to be the ratio of males to females at birth, so that for every female birth there will be 1 + s births of males and females. This implies that for every female child there will be 1 + s children, so N is replaced by (1 + s) N; for every sister there will be 1 + s siblings, so S is replaced by (1 + s) S. (Note that instead of one mother there will be exactly two parents.) The number of grandchildren (so ns and daughters of sons and daughters) will be (1 + s)2N2; the number of first cousins (sons and daughters of brothers and sisters of the mother or father) will be 2(1 + s)2SN; the number of nieces/nephews (so ns and daughters of brothers and sisters) will be(1 + s)2SN; and so on.
Like the applications given in Sect. 3 above, this second model of kinship only requires summary measures of the stable population (in this case S and N), and does not require any schedules of rates.
6. Conclusion
These applications have been presented largely at a conceptual level, without the specific data or numerical conclusions that might help to demonstrate their value. In each case, however, the original goal was to utilize stable population theory to draw approximate conclusions about real populations in situations where data are scarce. The model approximation has certain elegant formal properties and in effect permits the simulation of data that are generally not available for real populations. Indeed, significant improvement in the availability of demographic data is a likely reason why there have been relatively few new applications of the theory in recent decades.
Bibliography:
- Bourgeois-Pichat J 1971 Stable, semi-stable populations and growth potential. Population Studies 25: 235–54
- Cerone P 1987 On stable population theory with immigration. Demography 24: 431–8
- Coale A J 1981 Robust estimation of fertility by the use of model stable populations. Asian and Pacific Census Forum 8: 5–10
- Coale A J, Demeny P 1983 Regional Model Life Tables and Stable Populations, 2nd edn. Academic Press, New York
- Espenshade T J, Bouvier L F, Arthur B 1982 Immigration and the stable population model. Demography 19: 125–33
- Feeney G M 1970 Stable age by region distributions. Demography 7: 341–8
- Goodman L A, Keyfitz N, Pullum T W 1974 Family formation and the frequency of various kinship relationships. Theoretical Population Biology 5: 1–27. Addendum 1975 Theoretical Population Biology 8: 376–81
- Hinde A 1998 Demographic Methods. Arnold, London
- Keyfitz N 1971 Migration as a means of population control. Population Studies 25: 63–72
- Keyfitz N 1973 Individual mobility in a stationary population. Population Studies 27: 335–52
- Keyfitz N 1977 Applied Mathematical Demography. Wiley, New York
- Keyfitz N 1985 The demography of unfunded pensions. European Journal of Population 1: 5–30
- Keyfitz N, Nagnur D, Sharma D 1967 On the interpretation of age distributions. Journal of the American Statistical Association 62: 862–74
- Lapkoff S F 1991 A research note on Keyfitz’s ‘The demographics of unfunded pensions.’ European Journal of Population 7: 159–69
- Lesthaeghe R, Page H, Surkyn J 1988 Are immigrants substitutes for births? Unpublished paper, European University, Florence. Published in German in 1991 as Sind Einwanderervein Ersatz fur Geburten? Zeitschrift fur Bevolkerungs-wissenschaft 3: 281–314
- Lotka A J 1931 Orphanhood in relation to demographic factors: A study in population analysis. Metron 9: 37–109
- Mitra S 1983 Generalization of the immigration and the stable population model. Demography 20: 111–15
- Mitra S 1990 Immigration, below-replacement fertility, and long-term national population trends. Demography 27: 121–30
- Preston S H 1974 Effect of mortality change on stable population parameters. Demography 11: 119–30
- Pullum T W 1982 The eventual frequencies of kin in a stable population. Demography 19: 549–65
- Schoen R 1986 The two-sex multiethnic stable population model. Theoretical Population Biology 29: 343–64




