Sample Mathematic Models Of Population And Natural Resources Research Paper. Browse other research paper examples and check the list of research paper topics for more inspiration. iResearchNet offers academic assignment help for students all over the world: writing from scratch, editing, proofreading, problem solving, from essays to dissertations, from humanities to STEM. We offer full confidentiality, safe payment, originality, and money-back guarantee. Secure your academic success with our risk-free services.
Although the importance of the links between population and environment is widely appreciated, there is little agreement in the literature about the nature of these links.
Academic Writing, Editing, Proofreading, And Problem Solving Services
Get 10% OFF with 24START discount code
The dynamic link between population and natural resources—influences are never entirely unidirectional or constant over time—constitutes the main difficulty in assessing formal models and unified theories. To complicate matters further, this interrelationship depends on the level and type of economic activities, technological development, institutional settings and cultural systems. Even the variables themselves are not uniquely defined, but depend rather on the level and purpose of the analysis.
This research paper does not survey numerical simulation models of demographic economic environmental interactions (see Sanderson 1994 for a review), of which the World 3 Model (Meadows et al. 1972) is the most popular. Instead, it looks at some simple mathematical models that capture stylized facts of the link between population and natural resource dynamics. Such ‘mathematical cartoons’ help us to explain and understand how various population and environmental characteristics might affect each other, and they can teach us how to respond most effectively to various demographic and environmental developments.
Although it was exhaustible resources that first received theoretical attention, this research paper concentrates on renewable resources since these are the most interesting and least understood as regards changes in population structures and dynamics. In contrast to nonrenewable resources, the use of which is controlled largely by market prices, renewable ones are very often open-access resources. The overuse of resources if property rights are absent or poorly defined is called the ‘first tragedy of the commons’ (Hardin 1968) and can be corrected by restricting access to the resource. But as emphasized by Lee (1990), if the population is not fixed—as is presupposed in the models presented in this research paper—free access through reproduction constitutes the ‘second tragedy of the commons.’
1. Malthusian Population Dynamics And Natural Resources
The study of interactions between population and resources has a long history. According to Malthus, population growth reduces material welfare due to diminishing returns to labor on a fixed supply of land. On the other hand the higher the level of material welfare the higher the population growth rate will be. The Malthusian model predicts that ‘population will equilibrate with resources at some level mediated by technology and a conventional standard of living’ (Lee 1986). Improvements in technology will be offset in the long run by increases in the size of the population, but the standard of living will not be related to the level of technology. As such, the Malthusian model provides a description of a rather primitive society with incomes not too far above the subsistence level and where local renewable resources are an important part of the economic production process.
Renewable resources (agricultural land, forests, lakes, etc.) are not in fixed supply as Malthus assumed. Renewable resources regenerate, but if the rate of utilization (harvest) exceeds the rate of regeneration, a renewable resource will be depleted or, in the extreme case, irretrievably exhausted. By adding the dynamics of renewable resource growth to the dynamics of population growth, the Malthusian model is capable of explaining patterns of population growth and resource degradation that do not necessarily end up in a single equilibrium (Malthusian trap) (see Brander and Taylor 1998 and Prskawetz et al. 1994).
The structure of these models can best be described in terms of prey–predator dynamics, with the resources, R, being the prey and the population, P, acting as the predator. The dynamics of renewable resources (Eqn. (1)) are commonly described by the standard model of mathematical bioeconomics, where the net growth of the renewable resource, dR(t)/dt, is affected by two counteracting factors: indigenous biological growth, g(R(t)), and the harvest, H(R(t), P(t)), which depends on the stock of resources available to be harvested and the number of people who are harvesting. Indigenous resource growth is modeled by the logistic growth function g(R(t)) = aR(t)(K – R(t)), where the coefficient K determines the saturation level (carrying capacity) of the resource stock (i.e., K is the stationary solution of R if the resource is not degraded) and parameter a determines the speed at which the resource regenerates. The functional form of the harvest function is determined by the prevailing economic structure, and it establishes the link between the stock of resources and population. The population growth rate, (dP(t)/dt)/P(t) (Eqn. (2)), is modeled as an increasing function of material welfare y(t) = y(P(t), H(t)), which is determined by the level of the harvest and will be reduced by population growth. Whenever material welfare falls below the subsistence level, the population will decline. These Malthusian population dynamics imply that population growth may well adapt to resource constraints in contrast to models with exogenous positive population growth, where the economy collapses if resources do not regenerate quickly enough.
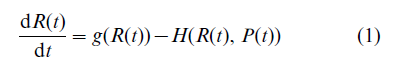
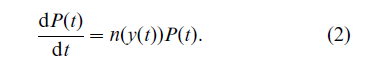
Within this class of models it is possible to investigate how the equilibrium between resources and population stock changes, dependent on the functional relations that govern the dynamics of population and resources. For instance, the efficiency of harvest technology, the degree of substitution between labor and resources, the indigenous rate of resource growth and the carrying capacity of the resource stock will have an effect on material welfare and hence on population growth. In turn, fertility and mortality will affect the resource dynamics via the input of changing labor stocks in the harvest. An empirical calibration of the model for the case of the small Pacific Easter Island characterized by pronounced population fluctuations was carried out by Brander and Taylor (1998).
Contrary to the Malthusian predictions, increasing population densities might be beneficial, as argued by Boserup (1981), and could well increase the human carrying capacity of the earth. Higher population densities will initiate technological innovations in agriculture, thereby increasing the yields so that the natural environment can support a larger population without reducing the level of welfare. Similar positive feedback mechanisms are captured in a simple mathematical cartoon of the interdependence between the growth in population P(t) and carrying capacity K(t) (expressed in numbers of individuals) by Cohen (1995) as
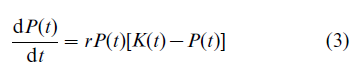
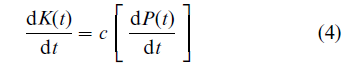
with r > 0 and c either negative, zero, or positive. The parameter c, which captures the effect of an increment of population on the carrying capacity, determines the long-term population dynamics, and it can represent technological innovation. When c = 1 population size grows exponentially (Euler, eighteenth century); when c < 1 population grows logistically (Verhulst, nineteenth century); and when c > 1 population grows faster than exponentially (Forester and co-workers, twentieth century).
Malthusian results (in the sense that population will grow to the point where material welfare matches subsistence demand) can be further undermined by allowing population growth to be a choice variable. Zero population growth may well be the optimal choice for individuals in the economy. Since environmental changes are often slow over the course of an individual life span, and since environmental damage may outlive its perpetrators, overlapping generation models (Eckstein et al. (1988)) provide an appropriate demographic structure. Intra as well as intergenerational conflicts can be modeled in such a framework, taking account of the effects of increases in population and resource exploitation on the future population’s quality.
The models presented so far represent traditional societies in which populations derive their living from primary occupations (agriculture, hunting, fishing, etc.) which depend on the availability of resources. But as societies become less bound to the land, more urbanized and more technological, they not only use the environment as a source of natural resources but also as a dump for waste products arising from human activity. Furthermore, an economy’s production possibilities are no longer determined by the maximum sustainable yield of renewable resources. Improvements in technology can increase the sustainable yields or reduce the resource stock required for production, and economic growth will allow for the use of manmade capital in place of natural resources. In open economies with trade, technological change, and economic growth, there is no simple and direct relationship between population growth on the one hand and the environment on the other hand.
Resources might still be at risk, albeit no longer by positive population growth alone. The risk can stem from the environmental costs of consumption and production. It is therefore of great importance to understand how these environmental impacts depend on different population structures.
2. The Impact Of Population On The Environment
In a seminal paper, Ehrlich and Holdren (1971) express the impact on the environment, I, (e.g., the value of some pollutant) as the product of population, P, and per capita impact, F(P):

Depending on whether diminishing returns or economies of scale are dominant, per capita impact can be increasing or decreasing in the total population. The most familiar form of such a demographic impact model is the so called I-PAT identity, which divides per capita impact F(P) into affluence A, and technology T. Affluence can be measured as GNP per capita, and technology represents the mean impact of an extra dollar of production (impact/GNP). The latter variable encompasses the cleanliness of technology, the effects of institutions, and other factors which can alter the impact efficiency of production.
Demographic impact models (Wexler 1996) constitute multiplicative identities aimed at decomposing the effect on the environment of population on the one hand and that of consumption and technology on the other. The number of variables on the right-hand side of Eqn. (5) can be any number greater than two. Although these models are commonly used, they face several criticisms. They suppress any feedback relation between the variables on the right-hand side; their implications are highly sensitive to the choice of decomposition variables; and the method of decomposition and the role of institutions and culture are ignored. Recent research on the I-PAT identity has dealt with some of these problems. Expressing the identity in terms of variances rather than means (Preston 1996) allows one to incorporate the links between the decomposition variables. Considering households instead of individuals as the unit of consumption (MacKellar et al. 1995) highlights the effect of economies of scale as household size increases. Typical results of such analyses are that the population has a much stronger impact on the environment in developing countries than in developed countries. In the case of environmental hazards produced by industrial processes, population growth plays a minor role both in developing and in developed countries.
Milik et al. (1996) embed the I-PAT identity into a dynamic model where population P, affluence A, and technology T influence each other and vary over time. Pollution I reduces the regenerative capacity of natural resources, which in turn influences the dynamics of population and affluence. The model highlights the fact that understanding and monitoring the impact of pollution on the environment is important even when outward signs of damage (as a reduction in the resource stock) are not yet visible. Ecosystems often absorb stresses over long periods of time and then eventually reach a disruption level at which the cumulative consequences of stress appear in critical proportions. A policy of waiting until the first signs of environmental deterioration are observed before actions are taken to reduce the impact on the environment may well prove to be disastrous. When action is initiated, the impact on the environment might already be irreversible. Mathematically, these systems can best be described in terms of ‘slow–fast’ dynamics, where during certain periods some variables vary much more rapidly than others. While population and economic variables can be regarded as slow moving variables, the environment changes most rapidly once the system has absorbed too much stress. For instance, the emission of carbon dioxide occurred almost unobserved for several decades before any attention was paid to the impact of greenhouse gases on global warming.
It becomes difficult to quantify the impact of population on the environment if the demand for local resources is not related to local population growth and if institutional environments are not stable. In fact, ‘commercialisation by converting a limited and inelastic subsistence demand to a limitless and elastic export demand (from the standpoint of the region, at least) can lead to much more rapid rates of exploitation than would be implied by population growth alone.’ (Repetto and Holmes 1983).
3. Modeling Environmental Influences On Population Dynamics
Existing models of environmental influences on population exhibit two shortcomings. First, they generally do not distinguish between the separate effects the environment may have on fertility and mortality. Second, the environmental impact on population growth is commonly modeled to work only through the economic and social variables of the model. There are only two examples in the literature that model the direct effect of environmental stress on fertility and mortality.
The first example (Nerlove 1991) is based on the vicious circle of poverty, population growth, and environmental degradation as evidenced in small rural communities of sub-Saharan Africa. In these economies simple tasks like fetching water and collecting fodder and wood are mostly carried out by children. This means that children are not only valuable to parents for future income but also as a source of current income. Higher population growth leads to more resource depletion, which reduces the marginal productivity of the resource. To offset this effect families have more children, thus depleting the resource even more. In a short parable Nerlove demonstrates that increasing the birthrate when the environment deteriorates will be the optimal choice for a household that maximizes per capita harvest when ‘the perceived marginal product of an additional child increases as environment deteriorates.’ In addition, in a system in which land rights are acquired through cultivation, a large number of children can imply increased claim to land ownership. This positive feedback between fertility and environmental degradation is in stark contrast to Malthusian dynamics, where population equilibrates with resources. Since the marginal private and social costs of reproduction are not the same, Nerlove then shows how social interventions in the form of taxes or subsidies can be used to induce a specific birthrate corresponding to a socially desirable stationary state.
The underlying mechanism of the above-mentioned vicious circle is neither population growth nor environmental degradation but poverty, which prevents the substitution of alternative fuel sources, and the low status of women and girls, which devalues the large amount of time and effort that they must devote to daily gathering activities. To escape this vicious circle one needs to alleviate poverty and to educate women.
As suggested by Chu (1998), the increasing specialization and level of economic activity typical of advanced societies may also imply a substantial dependency of population dynamics on the state of the environment. Increasing the level of human activities destroys the earth’s biodiversity, so that the ability of the environment to absorb negative shocks will decline, while increased specialization makes people less adaptive to environmental shocks. Chu suggests a simple mathematical model of the survival probability f(•,•) to capture both effects:
![]()
![]()
where mt denotes the logarithm of the number of intermediate goods (a measure of the division of labor) with mt < m t and xt is a realization of the environment value Xt with the critical state xt = 0. The mean and the variance of the random variable Xt will be increasing functions of mt. By reducing the ability to adapt, increased specialization mt will decrease the survival probability if the environment is already in a disastrous state xt < 0, while the opposite relation will hold if the environmental state is favorable xt > 0.
4. Concluding Assessment Of The Literature
Although there is a growing awareness of the population/environment linkage, as evidenced by the increasing number of empirical (case) studies, research has not progressed much in the Malthusian spirit of modeling the complex interaction in simple mathematical cartoons. Even worse, dynamic interactions between population and environment are often neglected—or increasingly complex simulation models are set up where anything can happen.
Further research on this topic is urgently needed. The concern should be shifted away from physical limits to growth towards the ability of social units to respond to environment population linkages. Although they are more difficult to formalize, such models should also include organizational and institutional issues. The study by Angelsen (1999) provides a first step in this direction.
Bibliography:
- Angelsen A 1999 Agricultural expansion and deforestation: modelling the impact of population, market forces and property rights. Journal of Development Economics 58: 185–218
- Boserup E 1981 Population and Technological Change: A Study of Long-Term Trends. University of Chicago Press, Chicago
- Brander J A, Taylor M S 1998 The simple economics of Easter Island: a Ricardo–Malthus model of renewable resource use. The American Economic Review 88(1): 119–38
- Chu C Y C 1998 Population Dynamics: A New Economic Oxford University Press, New York
- Cohen J E 1995 Population growth and earth’s human carrying capacity. Science 269: 341–6
- Eckstein Z, Stern S, Wolpin K I 1988 Fertility choice, land, and the Malthusian hypothesis. International Economic Review 29(2): 353–61
- Ehrlich P R, Holdren J P 1971 Impact of population growth. Science 171: 1212–7
- Hardin G 1968 The tragedy of the commons. Science 162: 1243–8
- Lee R D 1986 Malthus and Boserup: a dynamic synthesis. In: Coleman D, Schofield R (eds.) The State of Population Theory: Forward from Malthus. Basil Blackwell, Oxford, UK pp. 96–130
- Lee R D 1990 Comment: the second tragedy of the commons. Population and Development Review 16 (Suppl.): 315–22
- MacKellar F L, Lutz W, Prinz C, Goujon A 1995 Population, households, and CO emissions. Population and Development Review 21(4): 849–65
- Meadows D H, Meadows D L, Randers J, Behrens W W 1972 The Limits to Growth. Universe Books, New York
- Milik A, Prskawetz A, Feichtinger G, Sanderson W C 1996 Slow–fast dynamics in Wonderland. Environmental Modeling and Assessment 1: 3–17
- Nerlove M 1991 Population and the environment: a parable of firewood and other tales. American Journal of Agricultural Economics 73: 1334–47
- Preston S H 1996 The effect of population growth on environmental quality. Population Research and Policy Review 15: 95–108
- Prskawetz A, Feichtinger G, Wirl F 1994 Endogenous population growth and the exploitation of renewable resources. Mathematical Population Studies 5(1): 87–106
- Repetto R, Holmes T 1983 The role of population in resource depletion in developing countries. Population and Development Review 9(4): 609–32
- Sanderson W C 1994 Simulation models of demographic, economic, and environmental interactions. In: Lutz W (ed.) Population–Development–Environment: Understanding their Interactions in Mauritius. Springer, Berlin, pp. 33–71
- Wexler L 1996 Decomposing models of demographic impact on the environment. Working Paper WP-96–85, IIASA, Laxenburg, Austria




