Quality Control and Reliability Research Paper

An answer to the first part of this question lies in the thesis that the notion of reliability is useful for certain kinds of decision making under uncertainty, and that the normative approach to decisions is based on quantifiable inputs (see Lindley 1985). Thus, in a broad sense, quantified measures of reliability are inputs to normative decision making. The answer to the second part of the question depends on how reliability is defined, and this depends on how it is to be used. Thus, in psychological testing, reliability reflects consistency of results provided by a test instrument, and so quantification is based on a notion of consistency. By contrast, reliability used in the engineering sciences pertains to an attribute of functional quality, and this indeed is its connection with quality. Functional quality is an ability to satisfy a set of requirements, and reliability comes into play when the requirement is either survival, or an ability to perform. It is in this context that reliability is of interest. Here, the quantification of reliability becomes a subtle issue, because the approach used to quantify leads one to a philosophical debate, a debate that has plagued generations of thinkers. More about this will be said later. For now it suffices to say that reliability is a quantified measure of uncertainty about a unit’s survival for a prescribed time, or its ability to perform as desired. The unit can be biological or physical; when biological, reliability takes the label ‘survival analysis,’ a topic that has become the backbone of biostatistics.

2. Background: Interest In Reliability—Past, Present, And Future

Reliability is a quantification of a certain type of uncertainty. From a historical perspective, the quantification of this type of uncertainty dates back to Huygens, who in 1669 constructed what is now known as a ‘survival curve.’ Huygens’ work was based on Graunt’s data on vital statistics. Since the first ‘survival table’ was published by Edmund Halley in 1693, one may claim that statistical methodology, and statistical data analysis, have their origins in reliability. During the early 1930s, the problems of commerce and insurance sustained an interest in this topic, whereas between the 1950s and the 1970s, quantified measures of reliability were needed for engineering design, for government acquisitions in aerospace and defense, for enforcing regulation in drug approval, and in matters of public policy, such as the safety of nuclear power generators.

Landmark achievements during this period are the papers by Davis (1952) on the analysis of equipment failure, by Epstein and Sobel (1953) on life testing for the exponential distribution, by Kao (1956) for acceptance sampling based on the Weibull distribution, and by Grenander (1956) on the analysis of mortality measurement. The 1960s also heralded the birth of the mathematical theory of reliability, with Barlow and Proschan’s (1965) classic book summarizing the knowledge to date. This work essentially defined the subject and provided avenues of research for years to come. Also noteworthy are the book by Gnedenko et al. (1969) which summarized the Soviet work in the area, and Marshall and Olkin’s (1967) fascinating paper on modeling dependencies.

During the 1980s and the early 1990s, pressures of consumerism and competitiveness forced manufacturers to use quantified measures of reliability for specifying warranties particularly with regards to the credibility of software (see, for example, Singpurwalla and Wilson 1999). The late 1990s also began to see concepts of reliability used in business, economics, and finance, and in matters of political science, particularly disarmament and national security.

The continued importance of reliability is anticipated in the twenty-first century because of a growing reliance on the infrastructure of communication systems, transportation networks, distributed power grids, and civil engineering structures at earthquake prone zones. Major initiatives by government and industry are underway under the label of ‘infrastructure protection,’ and quantified measures of reliability are a key factor of these. Finally, an area of growing concern wherein reliability is poised to play a signal role pertains to the credibility of nuclear stockpiles in the face of test ban treaties (cf. Armageddon Moves Inside The Computer, The Washington Post, November 28, 1998).

3. Foundational Issues In Reliability: Is A Paradigm Shift Needed?

Reliability, as a quantification of a certain uncertainty, leads to philosophical issues that have been the subject of debate. These issues are prompted by several questions that arise naturally, the first of which is: whose uncertainty? Is it that of an individual or a group of individuals, or is uncertainty inherent and therefore universal? The second question is if uncertainty is to be quantified, what should the quantification be based upon? Should it be subject matter knowledge, collective judgement, hard data alone, or a combination of all the above? The third issue pertains to the strategy for quantification. Should it be probability and the calculus of probability or should it be alternatives to probability like possibility theory, belief functions, confidence limits, tests of hypotheses, etc.?

Much of the literature on reliability fails to acknowledge these issues; rather, the focus has been on methodology—not principles. All the same, a major portion of the written material on reliability regards uncertainty as being inherent or universal, and subscribes to the principle that uncertainty can be quantified only by means of hard data. Furthermore, it takes the position that probability and its calculus need not be the only way to quantify uncertainty. Consequently, the mathematical theory (cf. Barlow and Proschan 1965, 1975) treats all probabilities as being known, whereas the statistical literature emphasizes ‘life-testing’ (a way to generate hard data), confidence limits, tests of hypotheses, etc. Indeed, statistical reliability theory’s major export, the Military Standard 781C, wholeheartedly subscribes to the above approaches for describing uncertainty and for decision making. A more recent example is the book by Meeker and Escobar (1998). Whereas a use of this strategy may be meaningful in the context of mass phenomena, like the output of a continuous assembly line, its use for one of a kind items, like computer software or limited size populations, is ill-founded. Furthermore, approaches that rely solely on hard data tend to be ignored by the users. This in turn has undermined the role of statistics and calls for a paradigm shift for addressing the modern problems of reliability that have been raised by the engineering community. Does this mean that one should forsake the calculus of probability in favor of alternatives like possibility theory and fuzzy-logic that many are attracted to?

The answer to the above question is a cautious no! Despite some shortcomings of the probability calculus, there does not appear to be any need to forsake it. However, a paradigm shift is indeed necessary, but this has to do with the interpretation of probability, not an alternative to probability! To address the modern problems of reliability, problems involving one of a kind items for which there is little or no failure data but a lot of informed testimony, it is the interpretation of probability that matters. Specifically, one needs to subscribe to the subjective or the personal view of probability in its purest form, as advocated by de Finetti (1964) and by Savage (1972). In addition to facilitating reliability assessment of one of a kind items, the subjective view offers other advantages. First, it helps explain several results in reliability theory that have been obtained via purely mathematical derivations (see, for example, Lynn and Singpurwalla 1997, in Block and Savits (1997), and Kotz and Singpurwalla (1999). Second, it facilitates the development of normative decision making procedures for acceptance sampling and drug testing (see, for example, Lindley and Singpurwalla 1991 and Etzioni and Kadane 1993). Most important, the subjective view of probability enables the treatment of dependencies in system reliability assessment in a natural manner (cf. Lindley and Singpurwalla 1986). The matter of dependence has plagued reliability analysts for quite some time, because, it is often the case that independence is assumed in place of dependence, with the consequence that assessed reliabilities do not agree with actual experiences (cf. US Nuclear Regulatory Commission 1975, National Research Council 1998).

Thus, to summarize, the view is held (cf. Singpurwalla 1988) that the twenty-first century will see a paradigm shift in the methods for assessing reliability. This paradigm shift will entail the interpretation of reliability as a personal probability, and not the adoption of a new set of rules for describing and combining uncertainties.

4. Key Notions, Terminology, And Overview Of Developments

In what follows, the position that reliability is a personal probability about the occurrence of certain types of events is adopted. Since the most common event of interest is survival of an item, under specified conditions, for a duration of time τ, τ ≥ 0, the reliability of the item is defined as

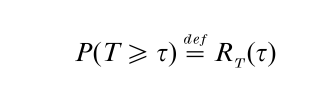
where P denotes probability, and T ≥ 0, stands for the item’s life-length. The interval [0, τ] is called the mission time, this terminology reflecting reliability’s connections to aerospace. The quantity R_T (τ), as a function of τ ≥ 0, is called the reliability function, and if the item is a biological unit, then this function is called the survival function, denoted by S_T (τ). Clearly, R_T (τ) decreases in τ, going from one at τ = 0, to zero, as τ increases to infinity. The life-length T could be continuous, as is usually assumed, or discrete when survival is measured in terms of units of performance, like miles traveled or rounds fired.

Let f_T (τ) be the derivative of – R_T(τ) with respect to τ ≥ 0, if it exists; the quantity

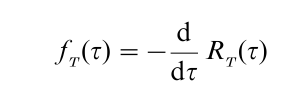
is the probability density of R_T(τ) at τ. When f_T(τ) exists for (almost) all values of τ ≥ 0, then R_T(τ) is absolutely continuous, and f_T(τ) is called the failure model. Much literature in reliability pertains to ways of specifying failure models. Classic examples are the exponential with a scale parameter λ > 0, i.e.,

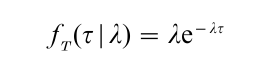
and the Weibull with a scale (shape) parameter λ (α) > 0, i.e.,

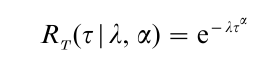
Other examples of failure models are surveyed in Singpurwalla (1995). The expected value of T

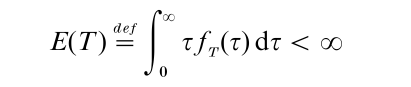
is called the mean time to failure (MTTF). For the exponential model

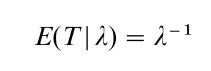
A concept that is specific and unique to reliability is the failure rate function or the hazard function. For an absolutely continuous R_T (τ), the failure rate function h_T (τ), τ ≥ 0, is

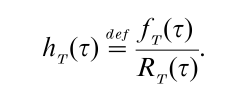
The failure rate function derives its importance from two features, one interpretative and the other, technical. Specifically, since

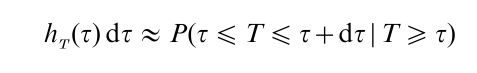
the failure rate at τ is (approximately) the probability of an item’s failure in [τ, τ + dτ), were the item surviving at τ. Clearly, for items that age with time, h_T(τ) will increase with τ, and vice versa for those that do not. This is the interpretative feature. The technical feature pertains to the fact that if

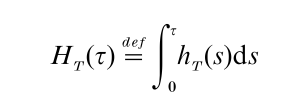
then

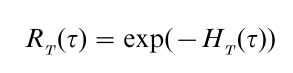
thus, knowing h_T(τ) is equivalent to knowing R_T(τ) and vice versa. The quantity H_T(τ) is known as the cumulative hazard at τ, and H_T(τ) as a function of τ is known as the cumulative hazard function. Bio-statisticians like Kalbfleisch and Prentice (1980) have used a continuously increasing stochastic process, like the gamma process, to describe H_T(τ) for items operating in a random environment. The connection between H_T(τ) and the Lorenz curve of econometric theory (see Gastwirth 1971) has been noted by Chandra and Singpurwalla (1981). This connection suggests that concepts of reliability have relevance to econometrics vis-a-vis measures of income inequality and wealth concentration.

It is easy to verify that when

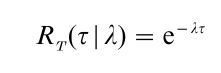
λ > 0, τ ≥ 0, h_T(τ|λ) = λ, and vice versa. Thus, under an exponential model, the failure rate is the reciprocal of the MTTF and vice versa. However, this reciprocal relationship holds only for the exponential, and not for all other distributions as practitioners often assume. An attractive feature of the Weibull distribution is that by choosing α to be greater (smaller) than one, the failure rate function can be made to be increasing (decreasing) with τ. When α = 1, the Weibull becomes an exponential. Because of this flexibility, the Weibull distribution has become one of the most widely used models in engineering reliability and survival analysis.

The failure rate function has become a cornerstone of the mathematical theory of reliability. Specifically, all models whose failure rate increases (decreases) monotonically have been classified into one group called the IFR (DFR) class (for increasing (decreasing) failure rate), and properties of this class have been studied. All properties are in relation to the exponential which is both IFR and DFR, since increasing (decreasing) in IFR (DFR) is taken to be nondecreasing (nonincreasing). The famous ‘bath-tub curve’ of reliability engineering pertains to a distribution whose failure rate is initially decreasing, then becomes a constant, and finally increases, just like an old fashioned bath-tub. This functional form is appropriate for describing the life-length of humans, and large systems of many components.

The mathematical theory of reliability has many interesting results, several of which are intuitive, but some not. One such unintuitive result states that a mixture of exponential distributions (which have a constant failure rate) has a decreasing failure rate. Another counterintuitive result states that the time to failure distribution of a parallel redundant system of components having exponentially distributed lifelengths, has an increasing failure rate, but is not necessarily monotonic. Both these results appear in Barlow and Proschan (1975), but the arguments used to prove them are purely technical. Their intuitive import is apparent only when we adopt the subjective view of probability; Barlow (1985) makes this point clear.

The reliability assessment of systems of components is relatively straightforward if the component’s lifelengths are assumed to be independent, the component’s reliabilities are assumed, and the system is not a network. When the component reliabilities are unknown, the life-lengths are dependent. This situation becomes even more complicated when the system is a network. Lynn et al. (1998) proposed a Monte Carlo approach for treating such problems. Dependence in system reliability can be treated by multivariate failure models of the type introduced by Marshall and Olkin (1967). However, the number of parameters of such models grows exponentially with the size of the system, so that even for moderate size systems a use of multivariate models becomes an onerous task. One way of overcoming this difficulty has been to assume that the component life-times are associated and then to argue that reliability assessments assuming independence provide bounds for the assessed reliabilities if dependence was incorporated. This strategy may be suitable for small systems, but with large systems the lower (upper) bound tends to zero (one), so that the bounding is effectively meaningless. There is a pressing need for new multivariate models with a small number of parameters; an example is in Singpurwalla and Youngren (1993).

Thus far, the discussion has been restricted to the case of a single index of measurement, namely time or some other unit of performance, such as miles. In many applications, both engineering and biomedical, the survival of an item is indexed by two (or more) scales. For example, automobiles under warranty are indexed by both time and miles. In the biomedical scenario, the onset of disease is recorded with respect to age and also the amount of exposure to a hazardous element. Failure models involving more than one scale are, therefore, germane and initial progress on this topic is currently underway. Such models are known as failure models with multiple scales; it is important not to confuse these models with multivariate failure models. The former pertain to a single unit, whereas the latter to multiple units.

5. Life Testing: Its Role In Reliability Assessment

Life testing is a scientific and controlled way of obtaining data. For those whose do not subscribe to the personalistic view of probability, data are mandatory for reliability assessment, and this includes the selection of a model. The data could be from a life test or from the field. For those who subscribe to the personalistic view, the actual data is desirable but not essential. Desirable because the role of the data is to update ones initial assessment of reliability. This is achieved by using Bayes’s law. The initial assessment of reliability is done by subjectively specifying a model and a prior distribution for parameters of the model, the prior also being subjective. The term subjective specification includes the use of expert testimonies (see, for example, Kadane and Wolfson 1998). The role played by the data, be it from a life test or the field, is to update the prior distribution to the posterior distribution.

Most life testing experiments are statistically designed experiments wherein several identical copies of the item whose reliability is being assessed are observed under conditions that replicate those of actual use. The life test is conducted until all items under observation fail or until a prespecified number fail. When the latter is done, the life test is said to be censored. The test can also be such that it is terminated after a fixed amount of time, irrespective of how many items fail in that time; such a life test is said to be a truncated test. A truncated test is terminated as soon as the last surviving item on the test fails. A life test can also be a combination of censoring and truncation, i.e., the test terminates at a fixed time or after a fixed number of failures, whichever occurs first.

When life tests are time consuming, it is common to make the conditions of the test harsher than those encountered in actual use. Such tests are called accelerated life tests, and tests with continuously increasing stress are those in which acceleration is done continuously (see De Groot and Goel 1979). Whereas accelerated life tests produce early failures, their disadvantage is that acceleration may induce changes in the material properties of the item, so that the failure behavior is different. Accelerated life testing has a parallel in the biological context; it goes under the name of dose–response experiments.

Whereas censoring and truncation can be well controlled in laboratory tests, actual data may have arisen from either scenario, and the analyst may not know from which. This is known as the stopping rule problem (see, for example, Roberts 1967). Interestingly, for a subjectivist, the stopping rule is immaterial (provided that it is noninformative). However, for those who do not subscribe to the Bayesian point of view, knowledge of the stopping rule is fundamental. In the absence of such knowledge they cannot proceed. A very readable account of the stopping rule problem is in Lindley and Phillips (1976). It is because of these and the other arguments mentioned before that reliability in the twenty-first century has to be not only Bayesian, but also subjective Bayesian!

Bibliography:

1. Barlow R E 1985 A Bayes explanation of an apparent failure rate paradox. IEEE Transactions Reliability R-34: 107–8
2. Barlow R E, Proschan F 1965 Mathematical Theory of Reliability. Wiley, New York
3. Barlow R E, Proschan F 1975 Statistical Theory of Reliability and Life Testing. Holt, Rinehart and Winston, New York
4. Block H W, Savits T H 1997 Burn-in. Statistical Science 12(1): 1–13
5. Chandra M, Singpurwalla N D 1981 Relationships between some notions which are common to reliability theory and economics. Mathematics of Operations Research 6(1): 113–21
6. Davis D J 1952 An analysis of some failure data. Journal of the American Statistical Association 47(258): 113–50
7. Epstein B, Sobel M 1953 Life testing. Journal of the American Statistical Association 48(263): 486–502
8. Etzioni R, Kadane J B 1993 Optimal experimental design for another’s analysis. Journal of the American Statistical Association 88(424): 1404–11
9. de Finetti B 1964 Foresight: Its logical laws, its subjective sources. In: Kyburg Jr. H E, Smokler H E (eds.) Studies in Subjective Probability. Wiley, New York
10. Gastwirth J L 1971 A general definition of the Lorenz curve. Econometrica 39(6): 1037–9
11. Gnedenko B V, Belyayev Y K, Solovyev A D 1969 Mathematical Methods of Reliability Theory. Academic Press, New York
12. Grenander U 1956 On the theory of mortality measurements, Part II. Skand Akt 39: 125–53
13. De Groot M H, Goel P K 1979 Baysian estimation and optimal designs in partially accelerated lift testing. Na al Research Logistics Quarterly 26: 223–35
14. Kadane J B, Wolfson L J 1998 Experiences in Elicitation. Journal of the Royal Statistical Society, Series D (The Statistician) 47(1): 3–19
15. Kalbfleisch J D, Prentice R L 1980 The Statistical Analysis of Failure Time Data. Wiley, New York
16. Kao J H K 1956 A new life-quality measure for electron tubes. IRE Transactions Reliability and Quality Control PGRQC-7
17. Kotz S, Singpurwalla N D 1999 On a bivariate distribution with exponential marginals. Scandinavian Journal of Statistics 26: 451–64
18. Lindley D V 1985 Making Decisions, 2nd edn. Wiley, London
19. Lindley D V, Phillips L D 1976 Inference for a Bernoulli process (a Bayesian view). American Statistics 30: 112–9
20. Lindley D V, Singpurwalla N D 1986 Multivariate distributions for the life lengths of components of a system sharing a common environment. Journal of Applied Probability 23(2): 418–31
21. Lindley D V, Singpurwalla N D 1991 On the evidence needed to reach agreed action between adversaries with application to acceptance sampling. Journal of the American Statistical Association 86(416): 933–7
22. Lynn N J, Singpurwalla N D 1997 Comment: ‘Burn-in’ makes us feel good. Statistical Science 12(1): 13–9
23. Lynn N J, Singpurwalla N D, Smith A 1998 Bayesian assessment of network reliability. SIAM Review 40(2): 202–27
24. Marshall A W, Olkin I 1967 A multivariate exponential distribution. Journal of the American Statistical Association 62: 30–44
25. Meeker W Q, Escobar L A 1998 Statistical Methods For Reliability Data. Wiley, New York
26. National Research Council 1998 Improving the Continued Airworthiness of Civil Aircraft. A Strategy for the FAA’s Aircraft Certification Service. National Academy Press, Washington, DC
27. Roberts H V 1967 Informative stopping rules and inferences about population size. Journal of the American Statistical Association 62(319): 763–75
28. Savage L J 1972 The Foundations of Statistics, 2nd rev. edn. Dover Publications, New York
29. Singpurwalla N D 1988 Foundational issues in reliability and risk analysis. SIAM Review 30(2): 264–82
30. Singpurwalla N D 1995 Survival in dynamic environments. Statistical Science 10(1): 86–103
31. Singpurwalla N D, Wilson S P 1999 Statistical Methods in Soft- ware Engineering. Springer, New York
32. Singpurwalla N D, Youngren M A 1993 Multivariate distributions induced by dynamic environments. Scandina ian Journal of Statistics 20: 251–61
33. US Nuclear Regulatory Commission 1975 Reactor Safety Study—An Assessment of Accident Risks in US Commercial Nuclear Power Plants. WASH-1400 (NUREG-75/014) October