Genetic Theories of Senescence Research Paper

1. Medawar’s Principle

The modern evolutionary theory of senescence begins with Medawar who argued that ‘… the efficacy of natural selection deteriorates with increasing age’ (1952, p. 23). A simple hypothetical example similar to a case considered by Hamilton (1966) illustrates the principle. Consider two genetic variants in humans, both having age-specific effects as follows: each variant confers complete immunity against a lethal disease, but only for one particular year of life. The first variant gives immunity to 12 year-olds, while the second variant confers immunity at the age of 60 years.

What are the relative selective advantages of the genetic variants? If, for simplicity, the effects of parental care are ignored and it is also assumed that menopause always comes before 60 years, then it is immediately obvious that the second variant is selectively neutral, having no effect at all on the ability of carriers to transmit genes to the next generation, whereas the first variant has a significant selective advantage. This example illustrates the general principle that natural selection is most effective in the young. To obtain a more exact and quantitative understanding of the relation between organismal age and the force of selection, it is necessary to develop a description of selection in age-structured populations.

2. Age-Structured Populations

Some organisms, such as annual plants, complete their life cycles in discrete fashion, exhibiting no overlap of parental and offspring generations. However, most higher organisms, including humans, have overlapping generations. Under the latter circumstances, the description of population composition and growth requires two kinds of information: age-specific survival, and age-specific fertility. Survivorship, denoted l(x), is defined as the probability of survival from birth or hatching until age x. A survivorship curve is a graph of l(x) versus x, where x ranges from zero to the greatest age attained in the population. The survivorship is initially 100 percent at birth and then declines to zero at the maximum observed age; it cannot increase with increasing age. If a cohort of 1,000 age-synchronized individuals are followed throughout their lives, then 500 of them will be alive at the age when l(x) is 0.50, 100 will be alive when l(x) is 0.10, and so on. Age-specific fertility, represented as m(x), is defined as the average number of progeny produced by a female of age x.

One of the fundamentals of demography is that, under a wide range of conditions, a population having fixed l(x) and m(x) schedules will eventually attain a stable age-structure. That is, after a period of time the proportions of the population in each age-class will reach unchanging values. If the survivorship or fertility schedules are altered, then a different age-structure will evolve.

Prior to attaining the stable age distribution, population growth is likely to be erratic, but once the stable age distribution is reached, then, under the assumption of unlimited resources, the population will grow smoothly. In particular, the population will exhibit exponential growth described by the following equation:

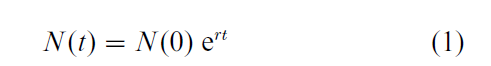
where N(t) is population size as a function of time t, N(0) is initial population size, e is the natural exponential, and r is the Malthusian parameter, also known as the intrinsic rate of increase of the population. The parameter r combines the effects of age-specific survival and fertility and translates them into a population growth rate. The value of r is the implicit solution to the following equation, known as the Euler–Lotka equation:

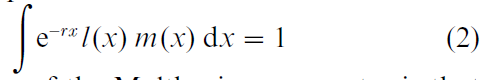
The significance of the Malthusian parameter is that it reflects fitness, in the Darwinian sense, in an age-structured population. If there are several genotypes in a population, and if those genotypes differ with respect to age-specific survival or fertility patterns, then each genotype will have a particular r value. Those r’s specify the rate at which a population consisting of only that genotype would grow, once the stable age distribution has been attained. The r’s also specify the relative fitnesses of the genotypes in a genotypically mixed population. The genotype with the highest r has the highest fitness and will be favored by natural selection under conditions that allow population growth. Much of the evolutionary theory relating to senescence and life histories uses the Malthusian parameter r as a surrogate for Darwinian fitness, essentially asking what changes in the l(x) and m(x) schedules would maximize the intrinsic rate of increase.

There is one other quantity that arises as a measure of fitness in populations with overlapping generations. Fisher (1930) defined ‘reproductive value,’ which is the expected number of progeny that will be produced by an individual of age x over the rest of its lifetime, given that it has survived to age x. Reproductive value is not the same as fitness, because it does not take into account the chances of surviving to age x.

3. Hamilton’s Perturbation Analysis

Hamilton (1966) asked the following question: What sorts of small genetic changes in the l(x) or m(x) schedules will be favored by natural selection? To answer this question he employed the Malthusian parameter r as a measure of fitness, assuming that the modifications of l(x) and m(x) that lead to the highest value of r will be the ones to evolve. He also approximated the continuous functions described above with their discrete-time counterparts. The discrete-time rate of population increase is:

The discrete-time version of the Euler–Lotka equation is

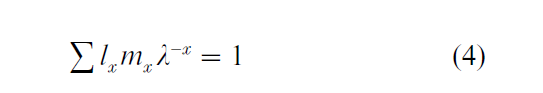
Age-specific survival is expressed in descrete time as:

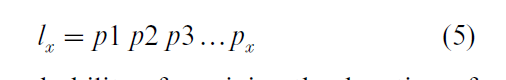
where p_x is the probability of surviving the duration of the xth age class given that one has survived to the beginning of age class x.

Now consider the evolutionary fate of a mutation which causes a small change in the ability to survive at some particular age a. The new mutation will be favored by natural selection if it causes an increase in r, or, what is equivalent in the discrete-time case, an increase in ln λ. The effect of the perturbation is studied by examining the partial derivative of λ with respect to p_a. Hamilton obtained a closed form of this derivative and was able to conclude the following:

(a) The force of selection, as indicated by the partial derivative is highest at the youngest pre-reproductive ages, begins to decline when reproduction commences and drops to zero when reproduction ceases.

(b) If a mutation causes a gain in survival at a particular age a₁ and an equal loss in survival at age a₂ , then such a mutation will increase in the population only if a₁ < a₂.

(c) If a mutation causes a gain in fertility at a particular age a₁ and an equal loss of fertility at age a₂ , then such a mutation will increase in the population only if a₁ < a₂.

(d ) If a mutation causes a loss in survival at a particular age and an increase in fertility at that same age, then the limits of the loss in survival that can be tolerated are set by the inverse of the reproductive value. That is, if the reproductive value at age x is large, then only a small reduction of survival can be exchanged for a gain in fertility, but if the remaining reproductive value is small, then a large reduction in survival can evolve.

(For further explication of these results, see Roughgarden 1996, p. 363.)

Hamilton’s general conclusion is that ‘for organisms that reproduce repeatedly senescence is to be expected as an inevitable consequence of the working of natural selection’ (1966, p. 26). This is a view that is clearly consistent with Medawar (1952). For a technical discussion of the validity of the assumption that the Malthusian parameter is equivalent to fitness in age- structured populations, see Charlesworth (1980), whose models extend the early results of Haldane (1927) and Norton (1928).

4. Pleiotropy

Pleiotropy means that a single gene affects two or more characters. In the context of life history evolution, pleiotropy means that a single gene affects the fitness of the organism at two or more ages. It is convenient to categorize the combinations of agespecific pleiotropic effects as shown in Table 1. If a new mutation improves fitness in both young and old animals, then it is likely to be favored by natural selection, and will increase in the population. Conversely, a gene that decreases fitness in both young and old organisms will be eliminated by natural selection. The more interesting cases in Table 1 are those in which the fitness effects on young and old organisms are negatively correlated, a condition referred to as ‘negative pleiotropy’ or ‘antagonistic pleiotropy.’ Medawar’s principle suggests that mutations that improve early fitness at the expense of late fitness will be favored by natural selection, while those with the converse effects will be eliminated.

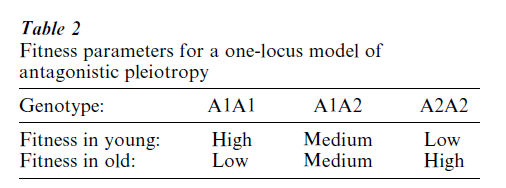
The possibility that genes might increase fitness at one age and also decrease it at another was mentioned by early theorists, but the first strong advocate of this mechanism of the evolution of senescence was Williams (1957), who noted that natural selection will tend to maximize vigor in the young at the expense of vigor later in life. An example of negatively pleiotropic gene action of the sort that Williams proposed is shown in Table 2. Williams argued that, in the course of selecting for the allele A1 which is beneficial at young ages, the deleterious effects of allele A2 on the old are brought along; in this scenario, senescence evolves as an incidental consequence of adaptation at earlier ages. The exact mathematical conditions for the increase of antagonistic, pleiotropic mutations have been derived (Charlesworth 1980), verifying that such mutations can indeed increase in populations.

While the theoretical basis for antagonistic pleiotropy is sound and widely accepted, it is unclear whether there exists the special sort of genetic variation that this mechanism requires. While it is easy to imagine physiological situations in which there could occur trade-offs between the fitness of the young and the old, there are few, if any, actual cases of such variation identified (Finch 1990, p. 37), even though a half century has passed since Williams’ proposal. Negative correlations between life history characters are sometimes construed as evidence for pleiotropy, but this interpretation overlooks the fact that phenotypic correlations arise from factors other than pleiotropy, including the correlation of environmental factors and the correlation of alleles at genetically linked loci (linkage disequilibrium). What is required for the antagonistic pleiotropy model is not just evidence of trade-offs in life history traits, which is abundant, but a demonstration that there exist tradeoffs in life history characters that are mediated by alternative alleles at specific polymorphic loci. Until such genes are characterized and shown to play a role in life history evolution, the antagonistic pleiotropy model will remain an interesting theoretical construct, but one of unknown, and possibly negligible, biological significance.

5. Mutation Accumulation

Germ-line mutations, which are changes in the DNA sequence in sperm and egg cells, occur at low but nonzero rates, largely as a result of proof-reading errors in the enzymes that replicate DNA. This slow, steady input of genetic variants has the potential to corrupt the gene pool, since almost all of the novel variants that have some effect are deleterious. However, natural selection works against the corrupting effect by removing carriers of deleterious mutations. A balance is reached between the steady input of deleterious genes through mutation and their removal by natural selection. One of the characteristics of the equilibrium balance state is that, for any particular gene, the deleterious alleles are present at low frequencies, usually much less than 1 percent. The low rate of occurrence of each of many hereditary human diseases is thought to reflect the mutation-selection balance operating at many genes, each of which is capable of being mutated to produce a deleterious condition (Hartl and Clark 1997).

The classical mutation-selection balance model is appropriate for mutations that have deleterious effects early in life, but what happens when the disability is expressed only late in life? Medawar (1952) suggested that natural selection will be unable to counteract the feeble pressure of repetitive mutation if the mutant genes make their effects known at advanced ages, either post-reproductively or at ages not attained by most of the members of the species. This follows naturally from his proposal that the force of selection declines with increasing age. Under such conditions, the deleterious mutations would gradually accumulate, unchecked by natural selection. In this view, senescence is a process driven entirely by mutation. This mechanism for the evolution of senescence is distinct from, but not mutually exclusive of, antagonistic pleiotropy. While the pleiotropy process suggests that senescence is the incidental consequence of adaptation, the mutation accumulation model invokes deterioration without adaptation (Partridge and Barton 1993).

Charlesworth (1980) has analyzed a deterministic model of an age-structured population with recurrent mutation. He derived an approximation for the frequency of heterozygous carriers of deleterious alleles and found that the equilibrium frequency is inversely proportional to the selection intensity. The significance of this result is that when there is only very weak selection pressure, as at advanced ages, then mutant alleles can attain high frequencies under the influence of recurrent mutation. This result verifies the earlier conjectures of Medawar and Williams. In contrast to the situation with antagonistic pleiotropy, there is experimental evidence for the kinds of genetic variation that the model requires, namely spontaneous mutations with age-specific effects on vital rates (Mueller 1987, Pletcher et al. 1998, 1999).

6. Postponement Of Deleterious Effects

Medawar (1952) also considered the case of Huntington’s chorea, a grave and ultimately fatal nervous disorder that usually manifests itself in middle-aged patients. He suggested that there could be selection in favor of genetic modifiers which have as their main effect the postponement of the effects of the Huntington’s gene or other genes causing hereditary disorders. This suggestion, which very much resembles an earlier proposal of R. A. Fisher concerning the evolution of dominance, is unlikely to be correct. While it makes sense that there would be some selection in favor of delaying the mutant effect, Charlesworth (1980, p. 219) has shown that the selection pressure exerted on such a hypothetical modifier gene would be exceedingly small, on the order of the mutation rate. This is because the modifier has an effect on fitness only when it co-occurs with the Huntington’s or other disease gene, which is at mutation-selection balance and present in only a small fraction of the population. Under such conditions the evolutionary fate of the modifier is likely to be determined by genetic drift or other stochastic factors rather than the minuscule selective pressure.

7. The Variation Problem

While the primary concern of theorists has been to explain the degeneration of vitality associated with old age, there is a secondary problem that can also be addressed with these models. Genetic variation is the raw material upon which natural selection operates to produce adaptations and new species. The mechanisms by which variation is maintained in populations are therefore of considerable interest to evolutionary geneticists. To what extent do genetic models of senescence tend to maintain variation in life histories within populations? Several authors have addressed the question and come to two different answers depending upon the theoretical construct employed. Curtsinger et al. (1994) analyzed deterministic one and two-locus models of antagonistic pleiotropy and asked under what conditions polymorphisms would be maintained. The conditions for stable polymorphism were found to be rather restrictive, especially with weak selection. The conditions were also found to be very sensitive to dominance parameters; in particular, reversal of dominance properties with respect to the two traits is often required for polymorphism, but seems improbable on biochemical grounds.

Tuljapurkar (1997) gives an overview of modeling strategies and describes some of his own models in which mortality is assumed to depend on both organismal age and random variables in the environment. In these models, the relative fitnesses are measured by a stochastic growth rate, which reflects average vital rates and environmental variability. Results from several related models show that phenotypic combinations that differ in age-specific fertility can be equally fit in a range of stochastic environments. The paper concludes that polymorphisms for length of reproductive life can be readily maintained by selection in temporally varying environments.

8. Future Directions

Two important challenges to the genetical theories of senescence arise from recent experimental work. The first challenge concerns mortality rates at advanced ages. Observations of survival in experimental organisms are usually presented in terms of age-specific survivorship, as defined in Sect. 2, but if sample sizes are sufficiently large then the survival data can also be analyzed in terms of hazard functions, which define the instantaneous risk of death as a function of age. Unlike survivorship, the hazard function can be nonmonotonic. Many experimental studies of moderate sample size have documented that the hazard increases approximately exponentially with age, a dynamic generally referred to as the Gompertz law (Finch 1990). Recent experiments have been done on an unusually large scale, making it possible to estimate hazards at very advanced ages. For Drosophila, nematode worms, and Med-flies, hazard functions increase exponentially in the early part of the life history, as expected, but at the most advanced ages the hazard functions decelerate, bending over and producing unexpected ‘mortality plateaus’ (see Vaupel et al. 1998, for a review of the experimental evidence and data on human populations).

The existence of mortality plateaus at advanced, post-reproductive ages poses a challenge for mutation accumulation models, which predict, under a wide range of assumption, a ‘wall’ of high mortality at the age when reproduction is completed. A preliminary attempt to accommodate mortality plateaus into antagonistic pleiotropy models has failed (Pletcher and Curtsinger 1998, Wachter 1999). One possible solution is that the mortality plateaus are caused by population heterogeneity of both genetic and nongenetic origin (Pletcher and Curtsinger 2000, Service 2000). It has so far proved very difficult to measure the relevant heterogeneity and determine whether it is of sufficient magnitude to produce the plateaus. A second possibility that can explain some features of the plateaus is a model of positive pleiotropy, which causes late-life mortality rates to avoid inflation because of the positively correlated effects of alleles selected for early survival (Pletcher and Curtsinger 1998). Models of positive pleiotropy merit further investigation.

The second experimental challenge to current theory concerns genetic variance. The mutation accumulation model predicts that genetic variance for mortality should increase at advanced ages. Recent experiments document instead a decline of genetic variance at advanced ages in experimental populations of Drosophila (Promislow et al. 1996). Hughes and Charles-worth (1994) initially reported that genetic variance for mortality increases with age in their Drosophila populations, but a re-analysis of the data show close concordance with the Promislow result (Shaw et al. 1999). At present no one knows why genetic variance declines at advanced ages; it could be related to the mortality plateaus described above.

Three other lines of research appear to hold promise. Group selection is a process by which collections of organisms succeed or fail as a collective, either becoming extinct or spawning new groups in competition with other groups. Groups selection arguments are sometimes invoked to explain altruistic behaviors, but evolutionary biologists typically disdain group selection, because the process tends to be much weaker than selection between individuals, and also seems to work only in very small populations ( Williams 1966). However, group selection might play a role in shaping post-reproductive mortality rates, when individual-level selection is essentially inoperative. This type of model could be particularly relevant to human evolution, and is essentially unexplored. A related type of model that needs further development involves the evolution of vital rates in combination with kin selection, taking into account the effects of post-reproductive survival, parental care, and fitness effects mediated through relatives in the kin group (Roach 1992). Finally, as noted by Tuljapurkar (1997), the theoretical methods are limited to small perturbations and local analyses, under which conditions the population is always close to demographic equilibrium. There does not exist at present a theory that can accommodate large mutational changes in vital rates in combination with non-equilibrium demo-graphics.

Bibliography:

1. Charlesworth B 1980 Evolution in Age-structured Populations. Cambridge University Press, Cambridge, UK
2. Curtsinger J W, Service P, Prout T 1994 Antagonistic pleiotropy, reversal of dominance, and genetic polymorphism. American Naturalist 144: 210–28
3. Finch C E 1990 Longevity, Senescence, and the Genome. University of Chicago Press, Chicago
4. Fisher R A 1930 The Genetical Theory of Natural Selection. Clarendon Press, Oxford, UK
5. Haldane J B S 1927 A mathematical theory of natural and artificial selection, Part IV. Mathematical Proceedings of the Cambridge Philosophical Society 32: 607–15
6. Hamilton W D 1966 The moulding of senescence by natural selection. Journal of Theoretical Biology 12: 12–45
7. Hartl D L, Clark A G 1997 Principles of Population Genetics, 3rd edn. Sinauer Associates Inc., Sunderland, MD
8. Hughes K A, Charlesworth B 1994 A genetic analysis of senescence in Drosophila. Nature 367: 64–6
9. Medawar P B 1952 An Unsolved Problem of Biology. H K Lewis, London
10. Mueller L D 1987 Evolution of accelerated senescence in laboratory populations of Drosophila. Proceedings of the National Academy of Sciences of the USA 84: 1974–77
11. Norton H T J 1928 Natural selection and Mendelian variation. Proceedings of the London Mathematical Society 28: 1–45
12. Partridge L, Barton N H 1993 Optimality, mutation, and the evolution of ageing. Nature 362: 305–11
13. Pletcher S D, Curtsinger J W 1998 Mortality plateaus and the evolution of senescence: Why are old-age mortality rates so low? Evolution 52: 454–64
14. Pletcher S D, Curtsinger J W 2000 The influence of environ-mentally induced heterogeneity on age-specific genetic variance for mortality rates. Genetical Research Cambridge 75: 321–9
15. Pletcher S D, Houle D, Curtsinger J W 1998 Age-specific properties of spontaneous mutations affecting mortality in Drosophila melanogaster. Genetics 148: 287–303
16. Pletcher S D, Houle D, Curtsinger J W 1999 The evolution of age-specific mortality rates in Drosophila melanogaster: Genetic divergence among unselected lines. Genetics 153: 813–23
17. Promislow D E L, Tatar M, Khazaeli A A, Curtsinger J W 1996 Age-specific patterns of genetic variance in Drosophila melanogaster. I. Mortality. Genetics 143: 839–48
18. Roach D A 1992 Parental care and the allocation of resources across generations. Evolutionary Ecology 6: 187–97
19. Roughgarden J 1996 Theory of Population Genetics and Evolutionary Ecology. An Introduction. Prentice Hall, Upper Saddle River, NJ
20. Service P M 2000 Heterogeneity in individual mortality risk and its importance for evolutionary studies of senescence. American Naturalist. 156: 1–13
21. Shaw F, Promislow D E L, Tatar M, Hughes L, Geyer C 1999 Towards reconciling inferences concerning genetic variation in senescence in Drosophila melanogaster. Genetics 152: 553–66
22. Tuljapurkar S 1997 The evolution of senescence. In: Wachter K W, Finch C E (eds.) Between Zeus and the Salmon. National Academy Press, Washington, DC, pp. 65–77
23. Vaupel J W, Carey J R, Christensen K, Johnson T E, Yashin A I, Holm N V, Iachine I A, Kanisto V, Khazaeli A A, Liedo P, Longo V D, Zeng Y, Manton K G, Curtsinger J W 1998 Biodemographic trajectories of longevity. Science 280: 855–60
24. Wachter K W 1999 Evolutionary demographic models for mortality plateaus. Proceedings of the National Academy of Sciences of the USA 96: 10544–7
25. Williams G C 1957 Pleiotropy, natural selection, and the evolution of senescence. Evolution 11: 398–411
26. Williams G C 1966 Adaptation and Natural Selection, A Critique of Some Current Evolutionary Thought. Princeton University Press, Princeton, NJ