Connectionist Models Of Concept Learning Research Paper

1. The Delta-Rule Model

One of the simplest and best understood learning rules in connectionist models is the so-called delta rule, which was proposed by Widrow and Hoff (1960) and which is formally equivalent to the learning rule in Rescorla and Wagner’s (1972) model of associative learning (see Sutton and Barto 1981). The delta rule is an error-correcting rule. It assumes that feedback is available on the classification performance of a net-work, and that this feedback is available for each stimulus that must be classified. A learning scheme that fulfills this condition is called a supervised learning scheme.

To illustrate the delta rule, assume that we have the following simple model of concept learning (Fig. 1). The model takes the form of a connectionist network, with two connected layers of processing units. The input layer is used to represent or encode the stimuli that can be presented, whereas the output layer represents the response alternatives (in a categorization context, each response alternative typically corresponds to a single category). Input coding is achieved by a number of units, each of which corresponds to a single feature or dimension of the stimulus. Furthermore, each input unit is connected to each output unit. The connections in the network have associated strength values. The strength of a connection determines the effect that activation of its source or input unit has on its output unit. In a network of this form, category learning is assumed to involve the modification of the strengths of the connections between input and output units, in such a way that presentation of a stimulus to the input units will give rise to the activation of the output unit that corresponds to the category to which the stimulus belongs.

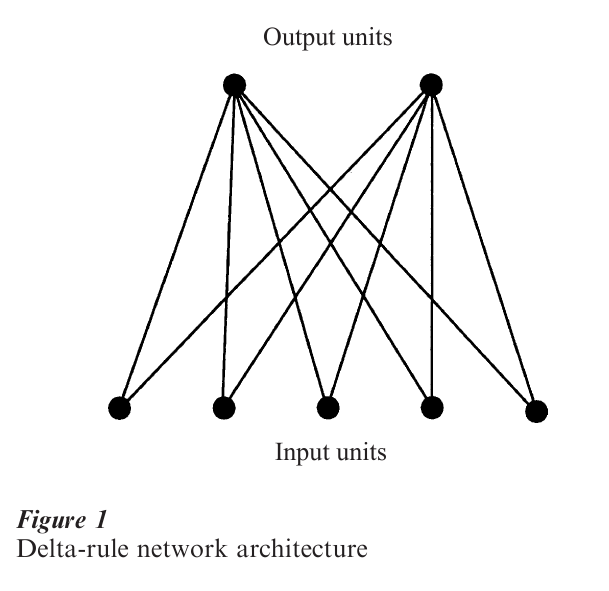
The input to the network on a given trial is represented by the pattern of activation across the input units. Suppose that each input unit represents a stimulus feature that can either be present or absent (such as ‘red,’ or ‘large’). The set of features that characterizes a stimulus can then be represented by setting the activation of each input unit that corresponds to a feature that is present to 1, whereas the activation of the other units can be set to 0. Of course, other representation schemes are possible, depending on the nature of the stimuli and the requirements of the learning task.

Upon presentation of a stimulus, the activation of the output units is computed, as follows:

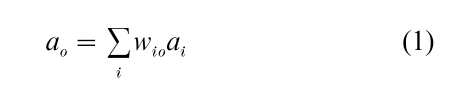
in which a_o is the activation of output unit o, a_i is the activation of input unit i, and w_io is the strength of the connection between input unit i and output unit o. Next, feedback about the network’s output activation pattern is provided, and the discrepancy between the current output pattern and the desired output pattern is computed. In a concept learning task, the desired output would typically be that one output unit (corresponding to the correct category) is activated, whereas the other units remain inactive. For each output unit, an error value e_o is computed:

in which do is the desired output value for unit o. Finally, the connection strengths in the network are modified, as follows:

in which δw_io is the change in the connection strength and in which λ is a learning rate parameter.

After a number of presentations of the entire set of stimuli in a category-learning task, the delta rule is guaranteed to produce a set of connection strengths that is optimal for the category-learning task at hand, within the constraints imposed by the architecture of the network (Kohonen 1977). For some category structures, the simple network in Fig. 1 is sufficient to achieve perfect categorization of all stimuli. If perfect categorization is impossible (for reasons that will be explained below), the delta rule still converges upon a set of connection strengths that produces the best performance that can be achieved with the network to which it is applied.

2. Evaluation Of The Delta-Rule Model

Delta-rule networks have been evaluated in a large number of empirical studies on concept learning (e.g., Estes et al. 1989, Friedman et al. 1995, Gluck and Bower 1988a, 1988b, Shanks 1990, 1991), with considerable success. However, although the delta-rule model can explain important aspects of human concept learning, it has a major weakness: It fails to account for people’s ability to learn categories that are not linearly separable. In a network of the kind described above, the activation of any output unit is always a weighted sum of the activation of the input units. This implies that the network can only learn categories that can be separated by a linear function of the input values. In human concept learning, linear separability does not appear to be an important constraint. It has been shown repeatedly that people can learn nonlinearly separable category structures without difficulty (e.g., Medin and Schwanenflugel 1981, Nosofsky 1987).

There are several ways in which delta-rule networks can be modified to handle nonlinearly separable categories. One way is to augment the input layer of the network with units that only become active when particular combinations of two or more features are present in the input (e.g., Gluck and Bower 1988b, Gluck 1991). If enough configural units are present (and if they encode the correct combinations of features), such networks can be made to learn any category structure using the delta rule. However, it is not clear that learning in such networks corresponds well to human learning, or that configural cue networks explain categorization after learning (Choi et al. 1993, Macho 1997, Nosofsky et al. 1994, Palmeri 1999). Moreover, the number of possible configural units grows exponentially as the number of stimulus dimensions becomes larger. Configural cue models are therefore not particularly attractive as models of human concept learning.

A second way of modifying delta-rule networks so that they can learn nonlinearly separable categories involves the use of a layer of ‘hidden’ units, between the input units and the output units. Rumelhart et al. (1986) proposed a generalization of the delta rule for such networks. This back-propagation-of-error rule is used to determine how much the connection strengths between input and hidden units, and between hidden and output units should be changed on a given learning trial, in order to achieve the desired mapping between input and output. If the units in such multilayer networks have nonlinear activation functions, back-propagation networks can learn nonlinearly separable categories; in fact, they can learn arbitrary mappings between inputs and outputs, provided that they contain a sufficient number of hidden units (Hornik et al. 1989).

Despite their intuitive appeal and obvious computational power, backpropagation networks are not adequate as models of human concept learning (e.g., Kruschke 1993). Their most important shortcoming is that they suffer from ‘catastrophic forgetting’ of previously learned concepts when new concepts are learned (McCloskey and Cohen 1989). To overcome this difficulty, Kruschke (1992) has proposed a hidden-unit network that retains some of the characteristics of backpropagation networks, but that does not inherit their problems.

3. ALCOVE

ALCOVE (Kruschke 1992, 1993) is a connectionist network with three layers of units: an input layer, a hidden layer, and an output layer (see Fig. 2). The model is based on an exemplar theory of concept learning and categorization, Nosofsky’s (1986) Generalized Context Model (GCM). Each input unit i of ALCOVE encodes a single stimulus dimension and is gated by a dimensional attention weight α_i, which reflects the relevance of the dimension for the learning task at hand.

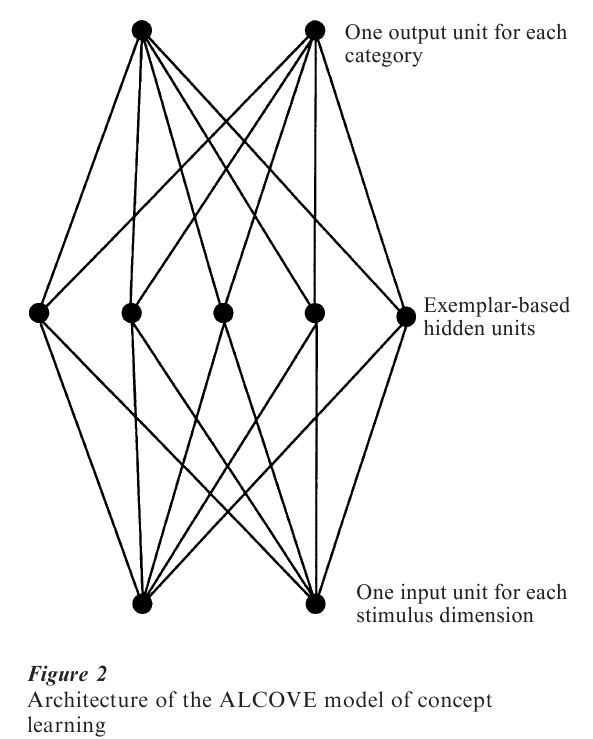
Each hidden unit has a ‘position value’ on each stimulus dimension, which means that each hidden unit corresponds to a particular stimulus or exemplar. Whenever an input pattern is presented to the network, each hidden node is activated according to the similarity between the stimulus it represents and the input pattern. In ALCOVE, similarity is defined as in Nosofsky’s GCM:

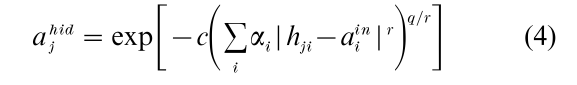
in which a^hid_о is the activation of hidden unit j, h_ji is the position of hidden unit j on stimulus dimension i, c is a positive constant called the specificity of the hidden unit, in is the activation of input unit aⁱⁿ_i, and where r and q determine the similarity metric and similarity gradient, respectively.

Each hidden unit is connected to output units that correspond to response categories. The category units are activated according to the following rule:

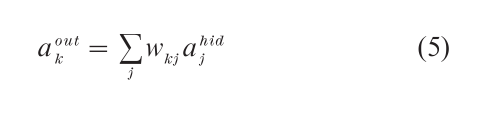
in which w_kj is the association weight between hidden unit j and category unit k. This is the same activation rule used in the simple delta-rule network discussed above (see Eqn. (1)). Finally, category unit activations are translated into response probabilities by the rule

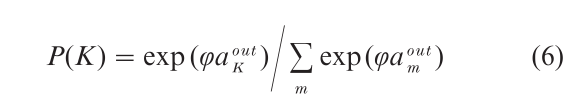
where φ is a scaling constant. ALCOVE employs a variation of the backpropagation learning rule to adjust dimensional attention weights α_i and association weights w_kj in the course of learning (see Kruschke 1992, for details of the learning rule). As a result of these adjustments, the network will eventually learn to classify each stimulus into the correct category.

ALCOVE has great advantages over the simple delta-rule network for concept learning. The model is not affected by the linear separability constraint. Like standard backpropagation networks, ALCOVE can learn arbitrary mappings between stimuli and categories. Moreover, ALCOVE does not suffer from catastrophic forgetting (Kruschke 1993). Most important, however, is the close correspondence between ALCOVE’s predictions about concept learning and human performance. In a large number of experiments, the model has been tested successfully (e.g., Choi et al. 1993, Kruschke 1992, 1993, Nosofsky et al. 1992, Palmeri 1999). ALCOVE ultimately derives its strength from its combination of the principles of exemplar-based processing with those of associative learning.

4. Conclusions And Future Directions

Whereas connectionist models such as ALCOVE can explain many important aspects of human concept learning, it is becoming increasingly clear that they also have fundamental limitations. The models that were reviewed here all assume that concept learning is an associative process, in which links between stimulus and category representations are modified. There is little doubt that many concepts are learned in this way. However, the associative model does not apply to the learning of all concepts. Some concepts are learned by a process of rule discovery, which has characteristics that are very different from those of connectionist models of learning. An important challenge for the future will be to determine when associative models and rule-based models of concept learning apply. There have been some recent attempts to develop hybrid models, which combine associative and rule-based learning principles (e.g., Erickson and Kruschke 1998), and it is likely that such models will become increasingly prominent.

Bibliography:

1. Ashby F G, Alfonso-Reese L A, Turken A U, Waldron E M 1998 A neuropsychological theory of multiple systems in category learning. Psychological Review 105: 442–81
2. Choi S, McDaniel M A, Busemeyer J R 1993 Incorporating prior biases in network models of conceptual rule learning. Memory and Cognition 21: 413–23
3. Erickson M A, Kruschke J K 1998 Rules and exemplars in category learning. Journal of Experimental Psychology: General 127: 107–40
4. Estes W K, Campbell J A, Hatsopoulos N, Hurwitz J B 1989 Base-rate effects in category learning: A comparison of parallel network and memory storage-retrieval models. Journal of Experimental Psychology: Learning, Memory, and Cognition 15: 556–71
5. Friedman D, Massaro D W, Kitzis S N, Cohen M M 1995 A comparison of learning models. Journal of Mathematical Psychology 39: 164–78
6. Gluck M A 1991 Stimulus generalization and representation in adaptive network models of category learning. Psychological Science 2: 50–55
7. Gluck M A, Bower G H 1988a Evaluating an adaptive network model of human learning. Journal of Memory and Language 27: 166–95
8. Gluck M A, Bower G H 1988b From conditioning to category learning: An adaptive network model. Journal of Experimental Psychology: General 117: 227–47
9. Hornik K, Stinchcombe M, White H 1989 Multilayer feed- forward networks are universal approximators. Neural Net- works 2: 359–66
10. Kohonen T 1977 Associative Memory: A System Theoretical Approach. Springer, New York
11. Kruschke J K 1992 ALCOVE: An exemplar-based connectionist model of category learning. Psychological Review 99: 22–44
12. Kruschke J K 1993 Human category learning: Implications for backpropagation models. Connection Science 5: 3–36
13. Macho S 1997 Effect of relevance shifts in category acquisition: A test of neural networks. Journal of Experimental Psychology: Learning, Memory and Cognition 23: 30–53
14. McCloskey M, Cohen N J 1989 Catastrophic interference in connectionist networks: The sequential learning problem. The Psychology of Learning and Motivation 24: 109–65
15. Medin D L, Schwanenflugel P J 1981 Linear separability in classification learning. Journal of Experimental Psychology: Human Learning and Memory 7: 355–68
16. Nosofsky R M 1986 Attention, similarity, and the identification-categorization relationship. Journal of Experimental Psychology: General 115: 39–57
17. Nosofsky R M 1987 Attention and learning processes in the identification and categorization of integral stimuli. Journal of Experimental Psychology: Learning, Memory, and Cognition 13: 87–108
18. Nosofsky R M, Gluck M A, Palmeri T J, McKinley S C, Glauthier P 1994 Comparing models of rule-based classification learning: A replication and extension of Shepard, Hovland, and Jenkins 1961 Memory and Cognition 22: 352–69
19. Nosofsky R M, Kruschke J K, McKinley S C 1992 Combining exemplar-based category representations and connectionist learning rules. Journal of Experimental Psychology: Learning, Memory and Cognition 18: 211–33
20. Palmeri T J 1999 Learning categories at different hierarchical levels: A comparison of category learning models. Psychonomic Bulletin and Review 6: 495–503
21. Rescorla R A, Wagner A R 1972 A theory of Pavlovian conditioning: Variations in the effectiveness of reinforcement and nonreinforcement. In: Black A H, Prokasy W F (eds.) Classical Conditioning II: Current Research and Theory. Appleton-Century-Crofts, New York, pp. 64–99
22. Rumelhart D E, Hinton G E, Williams R J 1986 Learning representations by back-propagating errors. Nature 323: 533–36
23. Shanks D R 1990 Connectionism and the learning of probabilistic concepts. Quarterly Journal of Experimental Psychology 42A: 209–37
24. Shanks D R 1991 Categorization by a connectionist network. Journal of Experimental Psychology: Learning, Memory, and Cognition 17: 433–43
25. Sutton R S, Barto A G 1981 Toward a modern theory of adaptive networks: Expectation and prediction. Psycho-logical Review 88: 135–70
26. Widrow C, Hoff M E 1960 Adaptive switching circuits. Institute of Radio Engineers, Western Electronic Show and Convention, Convention Record 4: 96–104