Computational Imagery Research Paper

This research paper considers diagrammatic or imagery-based reasoning primarily from the computational perspective. In particular, we consider the issues of how images or diagrams can be represented and used for automated reasoning. The applications of computational imagery in the context of problem solving is also considered. As this is a relatively new area of research in AI, there is not yet an agreed upon underlying theory or standard approach for problem solving with images. Therefore, this research paper presents an overview of approaches to this form of reasoning along with a description of various applications. A more detailed discussion of some of the issues presented here can be found in the book Diagrammatic Reasoning (Glasgow et al. 1995).

1. Reasoning With Images

A primary characteristic of a good formalism for knowledge representation is that it makes relevant properties explicit. Traditional approaches to knowledge representation and reasoning were developed primarily for linguistic or sentential reasoning, where-as computational imagery is concerned with emulating the problem solving abilities associated with mental imagery. Larkin and Simon (1987) have suggested that diagrammatic representations allow for the explicit representation and direct retrieval of depictive in-formation that is only implicit in the more traditional descriptive representations.

In the context of artificial intelligence, imagery can be considered as the ability to manipulate representations for the purpose of retrieving visual and spatial information that was implicitly, rather than explicitly, encoded in long-term memory. Marr (1982) has proposed three levels of analysis that are necessary to understand vision: computational theory, algorithmic and hardware (see Marr, Da id (1945–80)). Although all three levels of analysis can also contribute to the understanding of diagrammatic reasoning, this research paper focuses on the algorithmic level, which is concerned with the underlying representations and computational processes involved in problem solving with images or diagrams. A thesis of much work in computational imagery is that some of the processes involved are facilitated by depictive knowledge representation schemes that incorporate inferencing techniques based on direct inspection and transformation of the representation.

Computational imagery generally involves tools and techniques for visual and spatial reasoning, where depictive image representations are generated or re-called from long-term memory and then transformed, scanned, associated with similar forms (constructing spatial analogies), pattern matched, composed, and so on. Whereas visual reasoning is concerned with what an image looks like, spatial reasoning depends more on where an object is located relative to other objects in a diagram or a scene. This computational distinction is analogous to the distinction between visual and spatial models proposed in cognitive studies of imagery. Note that the representations generated to retrieve image information may correspond to real physical scenes or abstract concepts that are manipulated in ways similar to visual forms.

Funt (1980) proposed a computational approach to visual imagery that represents the state of the world as a diagram and actions in the world as corresponding to actions in the diagram. Similar to Kosslyn’s computational theory (1980), Funt uses two-dimensional arrays to depict visual images. In a more recent study of imagery, Chandrasekaran and Narayanan (1990) describe how visual information can be represented within the computational framework of discrete symbolic representations in such a way that both mental images and symbolic thought processes can be explained. Visual knowledge in this model is structured as multilevel hierarchies consisting of imaginal (two-dimensional pixel arrays) and symbolic (shape primitives) descriptions of the image configuration.

Lindsay (1988) suggests that depictive representations possess properties that help avoid ‘the combinatorial explosion of correct but trivial inferences that must be explicitly represented in a prepositional system.’ Sloman’s (1985) definition of analogical representations states that a representation is depictive if there is a correspondence between the structure of the representation and the structure of the image being denoted. More precisely, if D is a depictive representation of an image I, then (a) there must be a mapping of the parts in D (e.g., symbols or pixels) to parts in I, and (b) it must be possible to define a correspondence between properties or relations of parts of D and properties or relations of parts of I (e.g., shape, relative location, volume). In a vivid form of knowledge, there is also a one-to-one correspondence between symbols and objects in the world, and for every simple relationship of interest in the world there exists corresponding connections among symbols in the knowledge base. Levesque (1986) asserts that the main advantage of vivid knowledge bases is that they provide for efficient worst case reasoning behavior, since calculating what is logically implicit generally reduces to retrieving what is explicit.

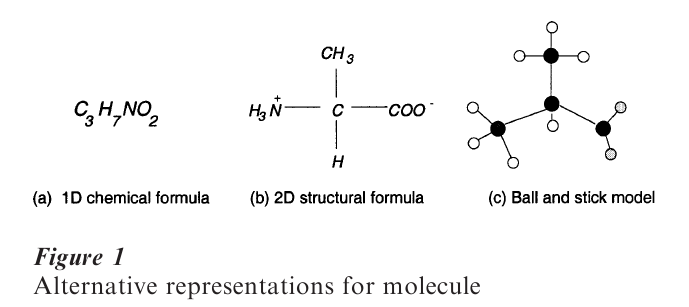
As a criteria for assessing alternative representations for shape description in vision, Marr (1982) introduced the concept of accessibility, which is defined as the ability to derive a representation from an image at reasonable computing costs. A similar criteria can also be applied to potential representations for imagery. Although formulating an image representation is often straightforward, constructing one that is efficient in terms of the amount of information stored, and also effective for problem solving, may be a complex process. For example, in the molecular domain it is possible to represent a structure in several different ways; our choice of representation depends on the questions we wish to ask. Take, for example, the multiple representations of a molecular structure illustrated in Fig. 1. If we wish to determine how many atoms of carbon are contained in a molecule, then the formula in Fig.1(a) is sufficient. However, if we need to derive connectivity, angle, distance or shape in-formation, then a more complex image representation, such as one corresponding to the illustration in Fig. 1(b) or (c), may be more appropriate.

Hayes (1974) discusses the notion of direct representations in which there exist similarities between what is being represented and the medium of the representation. Sloman (1985) has also argued the pros and cons of analogical representations, and has concluded that a variety of representation formalisms—including those specialized for spatial reasoning—are important to AI problem solving. Other hybrid approaches have been suggested for visual- spatial and model-based reasoning. Habel et al. (1993) have developed a system consisting of a propositional and depictorial partonomy (organization of parts) for reasoning, where the depictorial partonomy reflects the hierarchy proposed in representations for visual processes. They suggest that the advantage of the depictorial representation in the system is that it facilitates an efficient attention-driven method for reasoning. Myers and Konolige (1992) treat model-based manipulations as a form of inference within a classical logic system. More specifically, they store partially interpreted sensor data using an analogical representation that interacts with a general-purpose sentential language. A technique for qualitative spatial reasoning, based on the directional orientation information made available through perceptual processes, has been presented by Freksa and Zimmermann (1993). In this work, orientations in two-dimensional space are defined by the relation between a vector and a point.

Motivated by cognitive studies of mental imagery, Glasgow and Papadias (1992) have proposed a hybrid knowledge representation scheme for computational imagery consisting of three representations, each appropriate for a different kind of image processing: an image is stored in long-term memory as a hierarchically organized, descriptive representation; the spatial representation denotes image components symbolically and preserves relevant spatial and topological properties; and the visual representation depicts information such as shape, relative distance, and size. Imagery-based reasoning is carried out using primitive and high-level processes that construct, transform, and inspect visual or spatial representations.

2. Applications To AI Problem Solving

Visual-spatial reasoning techniques have also been considered in the context of specific application domains. Funt (1980) represents and manipulates a visual analog of a world in order to predict potential instabilities and collisions in a physical domain. Others have also used diagrammatic reasoning to simulate potential solutions for problem solving.

Epstein and Gelfand (1998) use spatial representations to generate potential moves in game playing. Barwise and Etchemendy (1993) have proposed a system called Hyperproof which integrates diagrammatic reasoning with sentence-based logics. Hyper-proof uses both diagrams and logic notation to teach students how to reason logically. They have also presented a formal semantics for reasoning with Hyperproof diagrams.

Research in geographical information systems and spatial databases has long been concerned with the issue of representing spatial knowledge. Samet (1989) has proposed a method for storing geographic knowledge based on the recursive decomposition of space. In this work, the term quadtree is used to describe binary array data structures that iteratively subdivide regions into segments until blocks are obtained that consist entirely of 1s or entirely of 0s. These structures (and their three-dimensional counterpart, termed octrees) are efficiently stored and implemented as trees, where each node of the tree corresponds to a region in the decomposition hierarchy. Another approach to reasoning in geo-graphic systems has been described by Papadias and Sellis (1993). In this work, a symbolic two-dimensional array structure is used to preserve a set of spatial relations among geographic entities.

Spatial representations have also been considered in a machine vision research. According to Biederman (1987), the representation of objects can be constructed as a spatial organization of simple primitive volumes, called geons. The process of image analysis, as defined by Marr et al. (1982), depends on a series of representations culminating in a three-dimensional model of the spatial relations among entities which makes explicit what is where. As in Marr’s approach to computational vision, research in molecular scene analysis (1993) is concerned with discovering what is present in the world and where it is spatially located. The act of determining the structure of a molecule is an interactive process consisting of a state space search of partially interpreted scenes, which can be represented and evaluated using processes from computational imagery.

Other problem domains where diagrammatic reasoning has been applied include qualitative physics, route planning, biology, human computer interaction, architecture, geometry, and theorem proving.

3. Future Research

Research in the area of diagrammatic and imagery based reasoning is still in its infancy. Most of the work to date has focused on individual applications where visual or spatial reasoning can provide a guide to problem solving. There are still many unanswered questions and areas to pursue that would lead us to a better understanding of how reasoning with images could improve problem solving in artificial intelligence. Some of the questions we might consider are:

(a) Are there general representation and reasoning techniques that cross application boundaries? Forbus (1993) has stated the Poverty Conjecture that claims: ‘there is no problem-independent, purely qualitative representation of space or shape.’ Whether this claim is true or not is clearly a topic for future research.

(b) How does diagrammatic reasoning interact with other reasoning paradigms in AI? Already, researchers have been investigating how image representations and reasoning techniques may interact with approaches such as rule-based reasoning or case-based reasoning. More work needs to be carried out to understand how such hybrid systems can best be constructed and applied.

(c) What can we learn from human cognitive models? The topic of mental imagery has long been studied in areas such as psychology, philosophy, and linguistics. Researchers in AI have much to learn from the understanding of how the human information processing system reasons with image representations.

(d) What are other potential domains of application for diagrammatic reasoning? Although several application areas have been considered, there are certainly other areas that would benefit from the ability to incorporate diagrams or images for the purpose of problem solving.

The area of diagrammatic reasoning is relatively new in AI. Prior to 1990 there were only a handful of papers related to this topic. Although interest and activity has greatly increased during the 1990s, there are still many questions to be posed and answered in this emerging area.

Bibliography:

1. Biederman I 1987 Recognition-by-components: A theory of human image understanding. Psychological Review 94: 115–47
2. Chandrasekaran B, Narayanan N 1990 Integrating imagery and visual representations. In: Proceedings of the 12th Annual Conference of the Cognitive Science Society. Lawrence Erlbaum Associates, Hillsdale, NJ, pp. 670–7
3. Epstein S, Gelfand J, Lock E 1998 Learning game-specific spatially oriented heuristics. Constraints: An International Journal 2: 239–51
4. Forbus K D 1993 Image and substance. Computational Intelligence 9(4): 309–33
5. Fortier S, Castleden I, Glasgow J, Conklin D, Walmsley C, Leherte L, Allen F 1993 Molecular scene analysis: The integration of direct methods and artificial-intelligence strategies for solving protein crystal structures. Acta Crystallographica D49: 168–78, Part 1
6. Freksa C, Zimmermann K 1993 On the utilization of spatial structures for cognitively plausible and efficient reasoning. In: Proceedings of the IJCAI ’93 Workshop on Spatial and Temporal Reasoning, pp. 61–66
7. Funt B V Problem-solving with diagrammatic representations. Artificial Intelligence 13: 201–30
8. Glasgow J, Papadias D 1992 Computational imagery. Cognitive Science 16(3): 355–94
9. Glasgow W J, Narayanan N H, Chandrasekaran B (eds.) 1995 Diagrammatic Reasoning: Cognitive and Computational Perspectives. AAAI Press, Menlo Park, CA
10. Habel C, Pribbenow S, Simmons G 1993 Propositional and depictorial partonomies: A hybrid approach. In: Proceedings of IJCAI ’93 Workshop on Principles of Hybrid Representation and Reasoning, pp. 62–71
11. Hayes P 1974 Some problems and non-problems in re-presentation theory. In: Proceedings of AISB Summer Conference, pp. 63–79
12. Kosslyn S M 1980 Image and Mind. Harvard University Press, Cambridge, MA
13. Larkin J H, Simon H A 1987 Why a diagram is (sometimes) worth ten thousand words. Cognitive Science 11: 65–99
14. Levesque H 1986 Making believers out of computers. Artificial Intelligence 30: 81–108
15. Lindsay R K 1988 Images and inference. Cognition 29: 229–50
16. Marr D 1982 Vision. W. H. Freeman, San Francisco
17. Myers K, Konolige K 1992 Reasoning with analogical representations. In: Proceedings of the Conference on Principles of Knowledge Representations and Reasoning. Morgan Kaufmann, Los Altos, CA
18. Papadias D, Sellis T 1993 The semantics of relations in 2d space using representative points: Spatial indices. In: Frank A U, Campari I (eds.) Spatial Information Theory: A Theoretical Basis for GIS: European Conference (COSIT ’93), Marciana Marina, Elba Island, Italy, September 19–22 proceedings. Springer-Verlag, Berlin, Vol 716, pp. 234–47
19. Samet H 1989 The Design and Analysis of Spatial Data Structures. Addison–Wesley, Reading, MA
20. Sloman A 1985 Why we need many knowledge representation formalisms. In: Research and Development in Expert Systems: Proceedings of the Expert Systems… the… Annual Technical Conference of the British Computer Society Specialist Group on Expert Systems. Cambridge University Press, for the British Computer Society, Cambridge, UK