Cultural Evolution Theory And Models Research Paper

Cavalli-Sforza and Feldman (1973, 1981) developed a quantitative theory for the cultural transmission and evolution of traits within populations. Such traits may be discrete valued or take values in a continuum. The idea here was to seek laws or principles that could explain observed levels of variation or estimated rates of change in a manner analogous to (but, of course, different from) those that have proven useful in evolutionary biology.

Durham (1991) has argued that the use of ‘cultural traits’ as the units of cultural transmission ‘pits nature against nurture.’ But if one simply uses ‘traits’ as units, then there is no implication as to how the trait is determined. This determination is defined by the model of transmission, which may be purely cultural, purely genetic, or some combination of these (Feldman and Cavalli-Sforza 1976, 1979). In principle, Durham’s alternative ‘ideational units’ are amenable to the same kind of quantitative analysis as that originated by Cavalli-Sforza and Feldman.

Boyd and Richerson (1985, p. 36) exclude ‘behavior and the products of behavior’ from the definition of culture because ‘behavior is contingent upon both patterns of thought and feeling and environmental circumstances.’ In following the example of Geertz (1973, pp. 44, 143–6) this exclusion would, if observed religiously, prevent most reasonable measurement and hence quantitative inference about cultural transmission and change. Many of the examples used by Boyd and Richerson, however, do actually involve behaviors as either the transmitted entity or the way in which the hypothesized entity is revealed and transmitted. Formally, at least, the structure of the theory in Boyd and Richerson (1985) is very similar to that of Cavalli-Sforza and Feldman (1973, 1981) and Feldman and Cavalli-Sforza (1976).

Units of cultural transmission have been assigned a variety of names beyond the ‘trait’ designation originally used by Cavalli-Sforza and Feldman (1973) and Feldman and Cavalli-Sforza (1976). Dawkins (1976) introduced the term ‘meme,’ which he later defined as a unit of information that is conveyed from one brain to another during cultural transmission. Lumsden and Wilson (1981) use the term ‘culturgen’ because they require that such traits are processed through ‘genetically determined procedures that direct the assembly of the mind.’ Each of these terms has disadvantages: ‘meme’ conveys a sense of imitation or involuntary allocation to memory, while ‘culturgen’ places too heavy emphasis on the ‘gen,’ and we know very little about which, or how many genes might be involved in human information processing. If a term is necessary, the recently introduced term ‘seme’ advocated by Hewlett et al. (2001) is attractive, with its connotations of semantics, signal, and communication.

1. Types Of Cultural Transmission And Their Consequences

Consider individuals in a large population at time t, where t is on a scale of generations, and generation t represents the parents of generation t+1. It is often useful to assume that these generations are non-overlapping with generation t physically replaced by generation t+1. Of course, for culturally transmitted entities, this may not preclude a contribution of generation t to generation t+2, for example. It is usually assumed that the population is censussed after cultural transmission has taken place. In the simplest models, the sexes are not distinguished, and each instantiation of the cultural trait may be regarded as taking a value from a set C, say.

1.1 Vertical Transmission

If an offspring’s probability of acquiring trait l in C depends on the traits j and k of its parents, we may represent the set of such transmission probabilities or rates as Γ ={β_jk,l}. Given the frequencies of each representation of the trait in the parental generation at time t, {x_i,t}, Γ determines {x_i,t+1} and the sequence of frequency vectors x₀, x₁,…, x_t … fully describes the evolution of the trait. Marriage between a pair of parents may occur at random, or we may assume, as is likely for many culturally transmitted traits, that individuals of the same trait value prefer to marry one another. This is called ‘assortative’ mating and occurs with probability m, say. An example of a dichotomous trait, that is one for which C contains the elements 0 and 1, is given in Table 1.

Then, if we write x_i´ for the frequencies in the offspring, that is, generation t+1, we have

where B=b₀₀-b₁₀-b₀₁+b₁₁, C=b₁₀+b₀₁-2b₁₁. Iteration of Eqn. (1) produces the complete evolutionary trajectory for the population frequencies of this trait. Note that b_00,0,=1, b_01,0=b_10,0,1/2, b_11,0=0 would be the expected transmission rule if 0 and 1 were genetic alleles of a sexual haploid biological organism. The closer the bs are to these values, the more the dynamic resembles a purely genetic evolutionary trajectory. But the system shows interesting flexibility; for example, if the probability that an offspring is unlike its parents is high enough, a cyclic trajectory results (Feldman and Cavalli-Sforza 1976).

Within the framework of vertical cultural trans- mission, the parameters {β_ij,k} may be disaggregated into separate additive contributions from each parent, although other partitions are conceivable. Estimation of these transmission parameters, for example under an assumption of equilibrium, is possible from familial correlations such as father–offspring or sib–sib correlations, while m is usually measured as the correlation between spouses. However, this may be biased by marital convergence.

Empirical studies designed to assess the importance of vertical transmission of everyday preferences among Stanford University students revealed that only religious and political attitudes were strongly vertically transmitted. Spousal correlations among the designated parents of these students were reasonably high, suggesting a moderate value for m (Cavalli-Sforza et al. 1982). Among the Aka pygmies, an African group of hunter-gatherers, however, vertical transmission of many customs was estimated by Hewlett and Cavalli-Sforza (1986) to be strong.

Evolution under long-continued vertical transmission should be conservative relative to that expected under other modes of transmission in the sense that change over generations is restricted by the extent of parent–offspring concordance. In particular, the more closely {β_ij,k} resembles a genetic transmission system, the slower will be the evolution. In fact, an exactly genetic transmission structure, in the absence of other forces, results in no temporal change at all. These points will be revisited in connection with continuous traits.

1.2 Horizontal And Oblique Transmission

Suppose that after vertical transmission the frequency of trait variant i in the population at time t+1 is x^V_i,t+1 and suppose that this particular variant, once acquired, cannot be lost. Then, in analogy with epidemic models of disease transmission, we suppose that individuals of type j (different from i ) who did not acquire i by vertical transmission contact those who did and are converted to i at rate f_ji, the rate of horizontal transmission. It is usual to assume 0 <f_ji<1. Then, after this transmission the new frequency of i is x^H_i,t+1 with

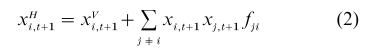
If the trait has only two variants 0 and 1, for example, then

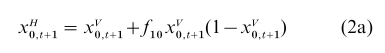
in which form the logistic nature of the dynamic becomes obvious.

Within the population, horizontal transmission will generally result in more rapid evolution, that is faster change in the frequencies of trait variants, than vertical.

Horizontal transmission modeled by Eqn. (2) occurs between members of the same demographic cohort. If the transmitters are in generation t (or earlier) and are not the parents of the acquirers of the trait, then we have oblique transmission. In most cases, oblique transmission will have similar consequences to same-cohort transmission, with a slight delay. However, an important special case of oblique transmission we have termed ‘one-to-many’ or ‘teacher-type’ trans-mission, which, in the strongest case, entails that a single individual at time t transmits to all individuals at time t+1. This results in exceptionally rapid evolution equivalent to the kind of cultural inbreeding often associated with modern mass media.

An important case of horizontal transmission is often called ‘cultural diffusion.’ The term generally applies to the trajectory of new cultural variant, an alternative to one that already exists and is dominant in the population. It can apply to the spread of the new variant within a single population or, if the population consists of several subpopulations between which there is some communication, it can refer to the spread across the collection of subpopulations. A logistic dynamic is often observed for the change in frequency of the new variant as it diffuses (e.g., Rogers 1995). An important question for many anthropologists is whether this diffusion may occur in the absence of migration of the people who carry the trait, and it is this case for which the term cultural diffusion is often reserved. On the other hand, if people move and carry their variant of the trait with them, and this variant diffuses with its carriers, the term ‘demic diffusion’ is commonly used. Distinction between these is usually difficult to make, but if genetic data are available that suggest a cline or gradient in allele frequencies from a putative source population of the human migrants (Cavalli-Sforza et al. 1993), then it might be reasonable to infer that demic diffusion has occurred.

The empirical basis of the conversion parameters {f_ji} in Eqn. (2) has been the subject of extensive sociological analysis. Rogers (1995) introduces the notion of awareness-knowledge, which is information that the new variant of the trait exists. Then there is the adoption phase, in which the decision to adopt may depend critically on local history of the variant, on the education level or economic status of earlier adopters vis-a-vis the decision-maker. Clearly, for the dynamics to be interpretable, simplification of the large number of parameters involved in these details is necessary. Hence the choice of {f_ji}.

It is possible to incorporate the idea of reinforcement through repeated transmission in both vertical and horizontal cases simply by iterating recursions Eqn. (1) or Eqn. (2) a number of times within a generation and censussing after this number of repeated operations. The rate of change across the new census points will be faster than that due to a single iteration per generation.

1.3 Group Effects And Conformity

The pressure on individuals within a population to adopt a belief or perform a task in a certain way may be affected by how many others in that population believe or act in that way. The result is that the transmission parameters, instead of being constant as in Eqns. (1) and (2), become functions of the frequency (or possibly frequencies). That is, for the dichotomous trait with horizontal transmission, f₁₀ in Eqn. (2a) might be an increasing function of x^V_0,t+1 when x^V_0,t+1 is large enough. This would amount to a pressure to conform to the majority. Boyd and Richerson (1985, Chap. 7) point out that this can accelerate the rate of cultural evolution. If the frequency-dependent transmission operates in different directions in different places, because of chance effects of environmental differences, this kind of conformity may also augment geographical differences between isolated groups. Applications to economic theory in terms of norms and preferences that are regarded as cultural entities have been initiated by Bowles (1998).

1.4 Innovation

In biological evolution, the ultimate source of all variation is mutation, nondirected random changes in the DNA that may or, more often, may not result in functional change in the organism. The equivalent for a cultural trait is the appearance of a new cultural variant, an innovation. The fate of an innovation within a population depends on its rules of trans-mission, which in turn may depend on a host of structural features of the trait itself. The analogue to the genetic phenomenon epistasis, which measures interaction between variants of different genes, is an example of a structural feature, but others would bear little relationship to the structural features that affect the fate of biological mutations. For example, stylistic variation in tool manufacture or behaviors that are coerced economically or by direct force would fall into this category.

In terms of the transmission law of Table 1, if b_00,1>0 or b_11,0> 0 an innovation has occurred in the offspring of the first or fourth matings, respectively. On a more general scale, an analogue to the infinite alleles models of population genetic theory (Ewens 1979, Chap. 3) is more appropriate to describe the stochastic dynamics of innovations, although this is an area that has had little formal study.

2. Continuous Traits And Linear Gaussian Models

If the trait under study varies continuously, then the transmission scheme is more difficult to represent. It is usual to represent the values of an offspring’s trait as X_t+1 and to specify that it is a weighted average of two randomly chosen parental values augmented by a random term:

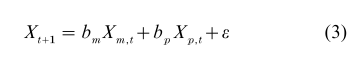
where b_m and b_p are maternal and paternal weights, and ε is the error random variable with zero mean and variance σ². Recursion (Eqn. (3)) corresponds to vertical transmission, and it is easy to include correlation between the parents (that is, assortative mating) as well as a kind of oblique transmission. The latter may be represented as a group effect g:

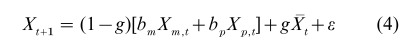
where X is the mean of the trait at generation t.

Several features of the dynamics resulting from models like Eqns. (3) and (4) are worth noting. The existence of a group-effect constrains the variance within the population (Cavalli-Sforza and Feldman 1981). If a number of groups are considered, however, within each of which transmission occurs as in Eqn. (4), then the variance, V_t, of the average across groups relative to the original group mean increases linearly with time: V_t = ktσ², where k depends on g, b_m, and b_f.

Linear models analogous to Eqn. (3) or (4) allow correlations between relatives to be computed rather simply, especially under Gaussian assumptions for the trait distribution. Indeed, the most widely used frame-work for studying familial aggregation of quantitative characters represents the genetic contribution to the character as a linear factor complementary to a linear environmental factor. With appropriate assumptions on the genetic term, variances and covariances be-tween relatives can be computed that mimic those calculated under the simplest genetic hypotheses (Fisher 1918). Controversy remains, however, about which joint linear model of genetically transmitted, culturally transmitted, and nontransmitted contributions to traits that aggregate within families is appropriate (Feldman and Otto 1997), while few attempts to use nonlinear representations have been made.

3. Natural And Cultural Selection

Most intuition about the effects of natural selection on genotypes comes from an interpretation of fitness as a relative probability of survival from fertilized egg to adult. However, a considerable body of experimental evidence (reviewed by Lewontin 1974, Chap. 5) suggests that differential fertility, sexual selection, and frequency-dependent effects are more important than differential survival abilities, although the former are more difficult to measure experimentally and to analyze theoretically. Despite these difficulties, it is reasonable to view natural selection on biological variation in terms of differential reproduction and survival. More details on the components of selection may be found in Hartl and Clark (1997, Chap. 6).

For cultural variants, natural selection on a trait may be understood in the same Darwinian way. To the extent that the variants of a trait affect the reproduction or survival of their carriers differentially, the frequencies of the variants will change over time accordingly. By contrast, cultural selection refers to differences in the rates of transmission of the cultural variants. As examples, such differences may be manifest in the rates at which individuals become aware of the alternatives or in the decision processes leading to the adoption of one or other of the alternatives. The results of cultural selection will be changes in the frequencies of the cultural variants in a population over time. One obvious difference from natural selection is that cultural may act within a generation rather like an epidemic (Rogers 1995). The parameters that summarize the process of cultural selection are the vertical, horizontal, or oblique transmission rates previously defined.

One area of theoretical debate concerns the possibility of conflicts between cultural and natural selection acting on the same variant of a trait. Thus, for the cultural trait of fertility, the variant whose carriers adopt fertility control (e.g., via contraception) is at a clear disadvantage in natural selection but has spread, especially in developed countries, by virtue of its advantage in cultural selection. Other examples are discussed by Cavalli-Sforza and Feldman (1981), Boyd and Richerson (1985), and Durham (1991). The debate, which cannot be settled with standard experimentation, centers on whether natural and cultural selection should act in the same direction most of the time. Alternatively, should the process of natural selection during human evolution have generally shaped cultural transmission in such a way that those variants favored by cultural selection are adaptive in the Darwinian sense?

A second contentious topic in debates about selection on a cultural trait concerns the role of group selection in the maintenance of variants which, within a group, are individually disadvantageous. Two kinds of models have been considered; in one there is extinction and recolonization of groups according to a stochastic process. If the probability of extinction of a group decreases with increasing frequency of the individually disadvantageous trait, then competition between the groups may preserve the disadvantageous trait. The usual example used for such analyses is altruism (e.g., Boyd and Richerson 1985, Chap. 7; Uyenoyama 1979). Maintenance of such a trait by extinction-type group selection is much less likely than by graded group selection, in which extinction does not occur but the expected relative contribution of a deme to the whole set of demes increases with the frequency of the altruist (Uyenoyama 1979). In the latter formulation, after reproduction there is redistribution of individuals to subgroups according to a stochastic process whose outcomes depend on the numbers of the disadvantageous types (Cohen and Eshel 1976). In other models, fluctuating environments in each of the subpopulations have been shown to allow group selection to occur under more general mixing conditions (Uyenoyama 1979). As pointed out by a number of authors, there are great similarities between these theories of group selection, and the Shifting Balance Theory of genetic evolution due to Sewall Wright (1931, 1935, 1948). On balance, there is a recent trend towards accepting the efficacy of an appropriately formulated model of graded group selection in maintaining traits that are individually disadvantageous, whether culturally or genetically transmitted. In particular, frequency-dependent cultural transmission, for example of the conformist type, may amplify differences between groups, thereby increasing the strength of group selection relative to that of natural selection within groups (Boyd and Richerson 1985).

4. Some Metatheoretical Considerations

Since around 1965, three main theoretical frameworks have formed the basis for the study of behavioral evolution and, in particular, human behavioral evolution. The first is kin selection theory, the second is evolutionary game theory, and the third is gene–culture coevolutionary theory.

Kin selection theory is due to W. D. Hamilton (1964) and is based on the idea that genetic alleles whose effect is disadvantageous on a carrier may be preserved if that carrier acts to increase the survival rate of other carriers of those alleles. These other carriers will most likely be relatives of the first carrier—hence the name ‘kin selection.’ By the mid-1970s, this theory had been extended beyond its original insect and animal boundaries to include human behaviors. In this process, the position that a wide array of behaviors would generally be genetically determined and adaptive, came to be called socio-biology (Wilson 1975).

During this period, the application of game theory, the second framework, to animal and human behaviors also became widespread. Here, in pairwise interactions for example, each individual was thought to optimize its behavior relative to the alternatives the other could adopt. The notion of optimization became prevalent in discussions of behavioral evolution (see, e.g., Parker and Maynard Smith 1990). Such treatments did not consider evolutionary dynamics as processes of frequency change but as processes of maximization of functions chosen by the investigator, usually to represent a measure of fitness.

Although such traits as altruism may well have a culturally transmitted basis, they have generally been studied in the theoretical literature using genetic models. Gene–culture coevolutionary theory was introduced as an alternative to the two former frame-works by Feldman and Cavalli-Sforza (1976). By allowing each individual a phenogenotype, the investigator is free to incorporate transmission mechanisms, selection functions, and dynamics that span the spectrum from purely genetic to purely cultural. Besides the obvious gain in flexibility to describe the evolution of behaviors, this framework also permits a natural statistical analysis of correlations between relatives a la Fisher (1918). The advantage here is that nongenetic effects are modeled more realistically than is possible using standard linear regression theory. In the coevolutionary dynamics with vertical cultural transmission, an association measure between the cultural and genetic variants is important and the order of magnitude of this association as a function of the comprehensive transmission rule can be derived. More details on the connections between these theories and the following examples can be found in Feldman and Laland (1996).

5. Examples Of Gene–Culture Evolutionary Theory

The evolution of lactose absorption was shown by Aoki (1986) to be well understood as a case of gene– culture coevolution. Here the gene in question is an autosomal dominant with lactose absorption the dominant phenotype at this locus. The cultural dichotomy is the presence or absence of a history of dairy farming. The frequency of lactose absorbers in populations with dairy traditions often reaches over90 percent, while in those populations without such a tradition it is typically below 20 percent. In modeling the joint evolution of the gene and the custom of dairying, both natural selection due to increased nutrition provided by milk and the cultural trans-mission of milk use, are affected by the genotype at the lactose absorbing locus. Analysis of this coevolution suggests that the fate of the absorption allele critically depends on the rate of vertical transmission of milk use. If this rate is very high, then a significant fitness advantage to absorbers can shift the frequency of the dominant allele to high frequencies in as few as 300 generations.

The spread of agriculture into geographical areas previously occupied by hunter-gatherers has been a fruitful subject for students of genetic and cultural history. Aoki and Shida (1996) used a reaction-diffusion process to model the spread of farming. Their analysis included a horizontal transmission process converting hunter-gatherers to farming as well as different intrinsic growth rates for initial farmers, converted farmers, and hunter-gatherers. Their analysis produced conditions under which farming would advance at a constant rate and, in addition, a gene frequency cline would simultaneously form. This elegant study represents a major advance over the earlier proposal of Ammerman and Cavalli-Sforza (1971), which was based on R. A. Fisher’s famous model for the advance of an advantageous gene (Fisher 1937).

A third example of gene–culture coevolution concerns the well-documented cultural bias against daughters in South and East Asia (Das Gupta 1987, Tuljpurkar et al. 1995). Under the assumption that a preference for sons is vertically transmitted, Kumm et al. (1994) studied how this transmission might affect the evolution of sex-determining genes. They showed that if parents act to increase the proportion of sons, irrespective of the biologically set sex ratio among their children, and if they compensate for lost daughters by having further children, the sex ratio will evolve to be female-biased. On the other hand, if parents try to achieve a desired sex ratio among their children and in so doing have fewer children than impartial parents, the primary sex ratio will become male-biased.

Bibliography:

1. Ammerman A J, Cavalli-Sforza L L 1971 Measuring the rate of spread of early farming in Europe. Man 6: 674–88
2. Aoki K 1986 A stochastic model of gene–culture coevolution suggested by the ‘culture historical hypothesis’ for the evolution of adult lactose absorption in humans. Proceedings of the National Academy of Sciences of the United States of America 83: 2929–33
3. Aoki K, Shida M 1996 Travelling wave solutions for the spread of farmers into a region occupied by hunter-gatherers. Theoretical Population Biology 50: 1–17
4. Bowles S 1998 Endogenous Bibliography: The cultural consequences of markets and other economic institutions. Journal of Economic Literature 36: 75–111
5. Boyd R, Richerson P J 1985 Culture and the Evolutionary Process. University of Chicago Press, Chicago
6. Cavalli-Sforza L L, Feldman M W 1973 Cultural versus bio-logical inheritance: Phenotypic transmission from parents to children (A theory of the effect of parental phenotypes on children’s phenotypes). The American Journal of Human Genetics 25: 618–37
7. Cavalli-Sforza L L, Feldman M W 1981 Cultural Transmission and Evolution: A Quantitative Approach. Princeton University Press, Princeton, NJ
8. Cavalli-Sforza L L, Feldman M W, Chen K H, Dornbusch S M 1982 Theory and observation in cultural transmission. Science 218: 19–27
9. Cavalli-Sforza L L, Menozzi P, Piazza A 1993 Demic expansions and human evolution. Science 259: 639–46
10. Cohen D, Eshel I 1976 On the founder effect and the evolution of altruistic traits. Theoretical Population Biology 10: 27–302
11. Das Gupta M 1987 Selective discrimination against female children in rural Punjab, India. Population and Development Review 13(1): 77–100
12. Dawkins R 1976 The Selfish Gene. Oxford University Press, New York
13. Durham W H 1991 Coevolution: Genes, Culture and Human Diversity. Stanford University Press, CA
14. Ewens W J 1979 Mathematical Population Genetics. Springer-Verlag, Berlin
15. Feldman M W, Cavalli-Sforza L L 1976 Cultural and biological evolutionary processes, selection for a trait under complex transmission. Theoretical Population Biology 9: 239–59
16. Feldman M W, Cavalli-Sforza L L 1979 Aspects of variance and covariance analysis with cultural inheritance. Theoretical Population Biology 15: 276–307
17. Feldman M W, Laland K N 1996 Gene–culture coevolutionary theory. Trends in Ecology and Evolution 11: 453–7
18. Feldman M W, Otto S P 1997 Heritability from twins and other relatives. Science 278: 1383–4
19. Fisher R A 1918 The correlation between relatives on the supposition of Mendelian inheritance. Transactions of the Royal Society of Edinburgh 52: 399–433
20. Fisher R A 1937 The wave of advance of advantageous genes. Annals of Eugenics. 7: 355–69
21. Geertz C 1973 The Interpretation of Culture. Basic Books, New York
22. Hamilton W D 1964 The genetical evolution of social behavior: Parts I and II. Journal of Theoretical Biology 7: 1–16, 17–52
23. Hartl D L, Clark A G 1997 Principles of Population Genetics, 3rd edn. Sinauer, Sunderland, MA
24. Hewlett B S, Cavalli-Sforza L L 1986 Cultural transmission among the Aka pygmies. American Anthropologist 88: 922–34
25. Hewlett B S, de Silverti A, Guglielmino C R 2001 Semes and genes in Africa. To appear
26. Kumm J, Laland K N, Feldman M W 1994 Culturally transmitted prejudices for offspring gender and the evolution of primary sex ratios. Theoretical Population Biology 46: 249–78
27. Lewontin R C 1974 The Genetic Basis of Evolutionary Change. Columbia University Press, New York
28. Lumsden C J, Wilson E O 1981 Genes, Mind and Culture. Harvard University Press, Cambridge, MA
29. Parker G A, Maynard Smith J 1990 Optimality theory in evolutionary biology. Nature 348: 27–33
30. Rogers E M 1995 Diffusion of Innovations, 4th edn. The Free Press, New York
31. Tuljpurkar S, Nan L, Feldman M W 1995 High sex ratios in China’s future. Science 267: 874–6
32. Uyenoyama M K 1979 Evolution of altruism under group selection in large and small populations in fluctuating environments. Theoretical Population Biology 15: 58–85
33. Wilson E O 1975 Sociobiology. Harvard University Press, Cambridge, MA
34. Wright S 1931 Evolution in Mendelian populations. Genetics 16: 97–159
35. Wright S 1935 Evolution in populations in approximate equilibrium. Journal of Genetics 30: 257–66
36. Wright S 1948 On the roles of directed and random change in gene frequency in the genetics of populations. Evolution 2: 279–94