View sample structures of personality traits research paper. Browse research paper examples for more inspiration. If you need a psychology research paper written according to all the academic standards, you can always turn to our experienced writers for help. This is how your paper can get an A! Feel free to contact our writing service for professional assistance. We offer high-quality assignments for reasonable rates.
Operations reshape concepts. Over the past decades, thevery concept of personality has been subject to implicit redefinition through a set of operations labeled the Big Five taxonomy or the five-factor model of personality. In a restricted sense, the number five refers to the finding that most of the replicable variance of trait-descriptive adjectives in some Western languages is caught by five principal components whose varimax rotations are named extraversion, agreeableness, conscientiousness, emotional stability, and intellect (or openness to experience, autonomy, imagination, and so on, depending on operational variations). In a wider sense, however, the five-dimensional (5-D) approach has come to represent no less than a paradigm—in particular, a revival of the individual-differences or trait conception of personality. For an evaluation of its status and future perspectives, a systematic analysis of its operational credentials is in order.
Academic Writing, Editing, Proofreading, And Problem Solving Services
Get 10% OFF with 24START discount code
A first module of the set of operations that constitute the 5-D paradigm consists of the questionnaire construction of personality, whereby someone’s personality is defined through his or her own answers, or more exceptionally through the answers given by third persons, to standardized questions. The questionnaire approach is not confined to the 5-D tradition, but it has to a significant extent been taken over by that paradigm (the megamerger impressing some as monopolistic). Is there a viable alternative to the questionnaire method, and if so, would it change our view of personality?
A second, more specific, operational module contains ways of choosing personality descriptors. The general guiding principle in this module is the lexical approach that consists of selecting items from a corpus of language, particularly a dictionary of that language. The distinguishing characteristic of the lexical approach is its purposely inductive nature, in contrast to approaches in which the descriptor base is deduced from particular trait constructs, for example, neuroticism. Again, the leading question is about the impact of these operations on our conception of personality.
A third operational characteristic consists of reliance on the linear model, particularly, principal component analysis (PCA) of Likert item scales. This is probably the most constitutive operation of the paradigm, if only because the number of five dimensions is intimately connected with it. The merits or demerits of PCAas such (if that problem makes sense at all) are not in order here. Clearly, however, other methods—notably, methods advocated under the label of person-oriented approach—yield concepts of personality that differ from the 5-D trait paradigm.
A fourth set of operations contains models for structuring, interpreting, and communicating trait information. The major rivals are the hierarchical and the circumplex models of personality structure. Their common point of departure is simple structure. On the one hand, simple structure is a primitive case of the circumplex in that trait variables are assigned to the factor on which they load highest, thus, to circle segments that are 90 deg wide with the factor poles as bisectrices. On the other, simple structure may be viewed as a primitive case of hierarchical structure containing two levels: factors at the top and trait variables at the bottom. But from there on, ways separate. I judge structure models by their capacity to produce clear and communicable trait concepts; their underlying mechanics, however, should be allowed to be intricate and may stretch the mind.
After discussing the structure models that have been proposed or implied in the 5-D context, I conclude with sketching a family of models that may serve as a base for capturing personality structure. It consists of a hierarchy of generalized semicircumplexes, with one general p component of personality at the top, and including two-dimensional circumplex, giant three, 5-D, and other dimensional structures. The joint structure responds to the greatest challenge in personality assessment, which is to deal with its dominating evaluative component in a realistic manner.
Constructing Personality Through Questionnaires
Under the 5-D paradigm, what does it mean to say that a person is extraverted? In the typical case, it means that this individual has given answers to a number of standard questions regarding himself or herself and that these answers have been summarized into a score under the hopefully adequate label of extraversion—rather than, for example, surgency or sociability, which are related but not the same. This is not to suggest that a ready alternative to the questionnaire approach is available; rather, it functions as a tacit presupposition in trait psychology taken generally. However, there is an obvious alternative to the individual himself or herself as a responder, namely, others who know the person well.
The Hegemony of Questionnaires
The association between personality and questionnaires is not merely a matter of fashion or a historical coincidence. To assess someone’s personality, we have to ask questions about it—to the person himself or herself, to third parties who know the person well, to expert observers. Between the investigator or practitioner on the one hand and the person on the other, there is an indispensable assessor. So-called behavior observations, for example, are not objective in the way they would be if behavior recordings were translated into a score without the intervention of an observer; they represent answers to questions put to a human assessor. Moving from asking questions to applying a questionnaire is a small step: Asystematic approach to personality requires standard questions, and thus a questionnaire. Using an unstructured interview, for example, means obtaining answers to an imperfectly standardized set of questions.
One seeming exception is self-report, in which person and assessor coincide. Failure to distinguish between the two roles, however, would amount to denying that the assessor could be someone else, thereby abandoning personality as an intersubjective phenomenon. Another more interesting apparent exception to questionnaire use is expert clinical diagnosis, in which practitioner and assessor coincide. In the first place, however, that process may be reconstructed in part as giving answers to more or less standardized questions about the person that the diagnostician has learned to ask to himself or herself. Second and more fundamental, the diagnostician could have been another individual. By virtue of that exchangeability, a case can be made for maximizing the intersubjective character of diagnoses. Actually using a standardized set of questions (e.g., a personality questionnaire phrased in the third person singular) to guide and articulate one’s diagnostic impressions would contribute to that end. This is not to deny the heuristic element in clinical diagnosis, or in any other applied setting, but to document the central place of asking questions to third persons in the systematic study of personality.
The reason for the primacy of questionnaires may of course be sought in a tendency of students of personality to take things easy: There is nothing more convenient than giving a self-report questionnaire to a client or applicant. But more valid reasons may be brought forward. There is a tension between the concepts of “test” and “personality.” Surely, we may decide to assess a person’s typical intelligent behavior by means of a questionnaire (e.g., Goff & Ackerman, 1992), or test the maximal introversion of which he or she is capable (see Riemann, 1997), but neither of these crossovers has appeared to be adequate or promising. Ability and tests of maximal performance, and personality and assessments of typical behavior, are associated in a nonarbitrary manner (Hofstee, 2001).
Are Questionnaires There to Stay?
The prime product of the 5-D paradigm consists of questionnaires, including most notably the Neopersonality incentives-PI-R and NEO-FFI (Costa & McCrae, 1992), and includes many other questionnaires and trait adjective lists; the model has thus given a significant boost to the questionnaire construction of personality. I have argued in brief that the relation between personality traits and the questionnaire operationalization is intimate. Should one be happy with the prospect of such an essentially monomethod definition of personality, and if not, can alternatives be foreseen?
Asking questions to third persons in order to assess personality implies a social definition of it. Surely, the field has moved beyond the stage at which personality was deemed to be merely in the eye of the beholder; cumulative behaviorgenetic research (Loehlin, 1992) has put an end to that subjective conception of traits. But the dominant conception of personality remains social in the sense of intersubjective rather than objective. Buss (1996) made a virtue of this need by explaining the Big Five as elementary social mechanisms; for example, Factor III represents the need of the perceiver to know whether the other person can be depended upon. Most students of personality, however, would have hesitations with this subordination of personality to social psychology, especially if that bondage is a side effect of a dominant operational approach.
The scientific emancipation of a subjective or intersubjective concept appears to hinge upon the discovery of objective indicators that cover the concept well. If we wish to establish how much of a fever we run, we do not use a Likert scale but measure it with a thermometer. If we want to gauge an applicant’s intelligence, we apply a test rather than asking questions to the applicant or even to a number of third persons. If the latter example is more problematic than the first, that is because there may be doubt regarding the coverage of the concept of intelligence by an IQ score. In the same vein, one may have doubts about the thermometer scale as a measure of outdoor temperature and prefer a formula that includes sunshine, humidity, and wind force. But once a certain level of coverage is secured, a return to sheer subjectivity would count as regressive. Are adequate objective indicators of personality traits in sight?
Probably the most promising indicators of personality are genes. According to estimates based on behavior-genetic research, genetic patterns will be capable of covering some 40% of the trait variance. That degree of coverage is not enough; we would not accept a thermometer that is only 40% valid. But before discarding the prospect, one should realize that the figure of .4 is heavily attenuated. An indicator need not and should not predict the error components in subjective assessments of temperature or extraversion. Heredity coefficients in the order of .4 should thus be divided by an estimate of the proportion of valid variance in questionnaire scores.
The first source of error in the self-reports that have almost invariably been used in behavior-genetic studies of personality is lack of agreement between assessors. The highest agreement coefficients between self and other in assessing personality (Hendriks, 1997; McCrae & Costa, 1987) are in the order of .7. Unless it is assumed that self is a systematically better assessor than other or vice versa, that figure may be taken as an estimate of the rater reliability of a single respondent, and some 30% of the questionnaire variance is rater error. Second, some 20% of the variance results from lack of internal consistency of the questionnaire scale, assuming alpha reliabilities in the order of .8; and third, a comparable error component results from temporal instability. Taking all these independent sources of error into account, one is left wondering how the heredity coefficients can reach .4 at all (Hofstee, 1994a).
The ironic conclusion from this crude analysis of error components in questionnaire variance is that the perspective of molecular-genetic diagnosis of personality traits cannot at all be discarded: It may well appear that whatever valid variance remains in questionnaire data can be accounted for to a satisfactory extent by genetic configurations. However, the analysis also points to the conditions for such a development. To establish links between genes and phenotypic personality traits, the assessment of the latter will have to be much more valid than it has been up to now (see also Bouchard, 1993). The central element of that program is discussed in the next paragraphs. Another aspect—optimizing the internal consistency of questionnaire data—is treated in the section on the linear approach to personality.
Definitions of Personality by Self and Others
Self-report fosters a conception of personality whereby the individual knows best how he or she is. With self-report questionnaires, the situation is more complicated. Standardized questions aim at comparing personalities rather than capturing unique and emergent characteristics. McAdams’s (1992) criticism of the Big Five approach as a psychology of the stranger is correct in that sense (although other phrasings might be preferred if the value of scientific objectivity is stressed); it would be even more correct if the emphasis in Big Five research were on other-report rather than selfreport. Self-report questionnaires embody a discordant blend of subjective and intersubjective accents.
In preparing an earlier (Hofstee, 1994a) paper on the topic, I met with unexpectedly ardent arguments in favor of self-report from prominent American Big Five researchers, the essence of which is documented in that paper. One argument pertained to personal secrets, whose content, however, would not be central to personality in most definitions. (A person might be said to be secretive, but that trait hardly even makes sense from the person’s own point of view.) Another argument was that a person might sit in a corner over a large number of consecutive parties but still consider himself or herself to be extraverted, which would be all that counts. In practice, however, most witnesses would start worrying whether that person were still in contact with reality (which is again different from the question about introversion or extraversion). In the abstract, actors are at liberty to entertain a subjective definition of personality, but in real life it does not carry them very far. The intersubjective viewpoint is not merely a matter of scientific style; it is in touch with what people think of personality.
If the intersubjective viewpoint is accepted as a proper perspective on personality and if idiosyncrasies in self-report are seen as a source of error among other sources of error, the consequence for personality research and practice is as straightforward as it is revolutionary: Multiple assessors are needed to achieve acceptable reliability and validity; self-reports, being single by definition, are inevitably deficient. Self is of course acceptable as an assessor among others; self-ratings might even contribute more to the common variance than others’ratingsdo.Butinanycase,theroadtowardaneventualobjective, genetic diagnosis of personality, will have to be paved with multiple assessors; good intentions will not be enough.
The Future of the Five-Dimensional Model
Will genetic fingerprinting in due time describe personality in terms of extraversion, agreeableness, conscientiousness, emotional stability, and some version of Factor V? In other words, will the 5-D model survive the developments that most readers may expect to witness in their lifetimes (whether they like it or not)? At the moment of writing this, the answer can hardly be unequivocal; even the question may appear to need rephrasing.
In an extensive reanalysis of several data sets, Saucier (2002a) found a three-dimensional structure containing agreeableness, conscientiousness, and extraversion to be more replicable across samples than a 5-D structure, especially in peer ratings, which in the present reasoning are more germane than self-ratings. So we might end up with a subset. Using a comparable three-dimensional solution, Krueger (2000) showed that the additive-genetic structure underlying the Multidimensional Personality Questionnaire (Tellegen, 1982) corresponded closely to the phenotypic structure. On the other hand, Jang, McCrae, Angleitner, Riemann, & Livesly (1998) demonstrated that specific factors beyond the first five have nonzero heritability coefficients.
Even supposing reliable and valid assessments of phenotypic personality traits, a routine search for indicators of, for example, conscientiousness would require enormous samples just for tracing additive polygenetic effects; for interactions, the required sizes would rise exponentially (for a discussion of strategies of molecular-genetic research on personality, see Plomin & Caspi, 1998). At the turn of the century, attempts to trace genetic polymorphisms that explain personality showed the familiar picture of high initial expectations followed by failing replications (e.g., Herbst, Zonderman, McCrae, & Costa, 2000). According to a possibly more feasible scenario, large principal components of personality traits may be expected to reappear as an aggregate result of studies searching for single genes to explain specific patterns of deviant behavior (see, e.g., Brunner, Nelen, Breakfield, Roppers, & Van Oost, 1993). Assuming continuity between the range of normal behavior and deviant extremes, the aggregate structure of a large number of such specific patterns would resemble the 5-D structure. In the process, such taxonomies of phenotypic traits would receive a status comparable to mineralogical classifications; the chemistry of individual differences would be located at the DNA level.
Decades ago, Carlson (1971) found that personality was spelled in either of two ways: social or clinical. The questionnaire conception of personality is arguably socialpsychometric by its methodological nature. If the genetic approach becomes dominant, a clinical reconstruction will regain momentum; individual differences within the normal range will be seen as mitigations and moderations of personality defects constituting the chemical elements. Meanwhile, an enormous amount of work has to be done, and 5-D questionnaires filled out by several third persons and self are instrumental in that labor.
The Lexical Base of the Five-Dimensional Model
A basic motive of researchers involved in the 5-D paradigm is to give a systematic and comprehensive, or at least representative, account of personality traits. An accompanying notion is that the field is characterized by a proliferation (John, 1990) of concepts and instruments, which frustrates the progress of the science of personality. The signature of the 5-D paradigm is empiricist and, in a sense, antitheoretical: If theorists, in this context, are individuals bent on disseminating their idiosyncratic concepts of personality, then their collective but uncoordinated action is responsible for a chaotic state of affairs in which thousands of unrelated concepts and their operationalizations form a market rather than a science. The 5-D conception is thus a taxonomy intended to end all idiosyncratic taxonomies.
To lift personality out of its chaotic state, an Archimedean point was needed. The most obvious candidate for a point of departure at the descriptive or phenotypic (Goldberg, 1993b) level is the lexicon. Like genetics, it provides a finite set of elements on the base of which a taxonomy may be built and proliferation may be counteracted. This section contains a discussion of the lexical point of departure, its variations, and its consequences. An analysis of the different shapes of the Factor V and their operational antecedents serves as an illustration.
The Lexical Axiom
What is usually referred to as the lexical hypothesis is more like an axiom. It states that people wish to talk about whatever is important and that the terms in which they talk may be found in the lexicon. The first and central part of that statement is not a hypothesis that is subject to empirical confirmation or disconfirmation; it introduces a heuristic that may or may not appear to be fertile. The second part is definitely false as no dictionary is ever complete; however, it is unproblematic because most dictionaries contain far more words than most people care to use or even understand, and hardly if ever omit common terms.
An objection that is seldom voiced although it is obvious enough is that the reverse of the lexical axiom does not necessarily hold true: People may well be talking about unimportant things most of the time. There is something to be said for the idea that the language of normal personality does not serve much of a purpose. However, PCA (see the next section) capitalizes on redundancies among variables. That method thus retroactively introduces a corollary of the lexical axiom, namely, that redundancy is indicative of real importance. For playful purposes, we may seek rare and sophisticated terms or combinations of terms; at the level of common components, however, we mean business. Of course, this corollary, in its turn, may or may not be judged credible.
A reverse objection is that common language is not subtle enough for scientific purposes. One may philosophize at length about this proposition, which is as metaphysical as the lexical axiom itself. The historic rebuttal, however, was delivered by Digman (1990; Digman & Inouye, 1986), who recovered the Big Five structure in questionnaires, that is, in instruments designed by experts. In a similar vein, I (Hofstee, 1999) asked 40 clinicians to score a prototypical personality disorder with which they were familiar on the items of the Five-Factor Personality Inventory (FFPI; Hendriks, Hofstee, & De Raad, 1999). These items do not contain any technical terms or pathological content. Nonetheless, very distinct and extreme profiles in 5-D terms resulted, again indicating that expert categories may be well represented by ordinary language.
In principle, the lexical approach both reflects and fosters a lay definition of personality; in practice, however, the effect seems to be slight. Thus, at low conceptual costs 5-D research has succeeded in bringing a considerable measure of order to the anarchy of phenotypic traits. Any serious investigator proposing a new trait concept would now be well advised to investigate whether it has incremental validity over an optimal linear combination of the five factors; existing concepts are better understood in that framework. An example is typical intellectual engagement (Goff & Ackerman, 1992), which appears to be a label for a mixture of Factors V and III; another is the familiar concept of sociability, blending Factors I and II. As I argue later, there is nothing against using dedicated labels for blends if they are distinguished from variables that do carry considerable specific variance. But even if taken liberally, the five factors represent a taxonomic breakthrough, part of which may be credited to the lexical approach.
Operationalizations of the Lexical Approach
There is no unique and cogent operationalization of the lexical approach. It pertains to single personality-relevant words, under the tacit supposition that words do not interact, so that the meaning of any trait combination can be represented by a linear function of them. That supposition is patently false in the case of oxymora like “amiably inimical” or “quietly exuberant,” joinings of opposite terms whose meaning cannot be accounted for in a linear fashion; however, there are reasons to be wary of such seductions of literary language. In any case, the search for single words is a defining characteristic of the lexical approach. But the question of how to select the single words has no straightforward answer; a number of decisions must be made.
A first decision concerns grammatical categories. Most investigators, from Galton (1884) on, have concentrated on adjectives (for an overview, see De Raad, 2000; Saucier, Hampson, & Goldberg, 2000). Goldberg (1982) and De Raad (1992) have studied type nouns, alphabetically running from ace to zombie in American English, but there is a consensus that this category does not add much (cf. extraverted vs. an extravert) or consists of invectives that have uses other than describing personality.Amore interesting addition to adjectives are personality-descriptive verbs, which run from abandon to yield (not counting zap, zip, and zigzag) in English, denoting acts that would be more characteristic of one person than another. De Raad’s (1992) analyses of personality verbs and nouns, however, do not result in novel content over the factors found in adjectives. The focus on adjectives does not recoil significantly on the implicit definition of personality.
A second set of operations consists of exclusion categories, for example, moods (e.g., sad), body characteristics (e.g., fat), social relations (e.g., subordinate), attitudes (e.g., progressive), and effects (e.g., famous). These exclusions are unproblematic because the categories are outside the domain of personality traits. Two other categories, however, deserve special consideration. One is called mere evaluations (e.g., good). In the language of personality, content and evaluation are intimately connected: On the one hand, neutral content is hard to find; on the other, mere evaluation is equally scarce. Tellegen (1993), in particular, has argued against excluding this category and has shown that it contains variance over and above the five factors (Almagor, Tellegen, & Waller, 1995). Thus, the 5-D model entertains a conception of personality that is somewhat sterilized with respect to evaluation.
The other problematic category is one that is invariably included, containing adjectives denoting intelligence, capabilities, talents, erudition, and the like—thus, the kind of maximum-performance traits that have traditionally been distinguished from typical-behavior traits. This inclusion is not an automatic consequence of the lexical approach; Ostendorf (1990), for example, sharply distinguished between temperament and character on the one hand, and skills and talents on the other, before joining the two sets of traits under the heading of dispositions. One could simply state that the 5-D approach has opted for the broader of the two definitions of personality, including not only temperamental or stylistic aspects (most notably Factors I, extraversion-introversion, and IV, emotional stability vs. neuroticism) and character (most notably Factors II, agreeableness, and III, conscientiousness), but also intellect, erudition, and the like (Factor V; see Hofstee, 1994b). However, I voice some reservations regarding that inclusive choice when discussing Factor V later.
A final operation consists of the exclusion of technical, highly metaphorical, and otherwise difficult terms. As I argued earlier, that procedure is probably not very consequential with respect to the scientific concept of personality, even though the literary loss is considerable. In constructing the FFPI, however, Hendriks (1997) went one step further and retained only items that were found perfectly comprehensible by students of lower professional education. Of the 1,045 brief expressions (e.g., Wants to be left alone) that made up the pool from which the items were chosen, 34% met this criterion. In a set of 195 trait-descriptive adjectives carefully selected to cover the factors of the 5-D model, only 14% did. It is a sobering thought that the founding studies of the 5-D model could not have been meaningfully carried out with these respondents. Furthermore, this sharpening of the comprehensibility criterion does appear to have consequences for the content of Factor V, as is shown next.
The Credentials of the Fifth Factor
The most spectacular vindication of the 5-D model has been brought forward by Ostendorf (1990). In the introduction to his study, Ostendorf related that he viewed the model with great skepticism at first, as the available American studies were based on very small samples of trait variables that had been composed using very subjective criteria (Ostendorf, 1990, p. 9). Not only this initial skepticism, but also the fact that the replication was completely independent, started from scratch, and was carried out in another language, added to the credibility of the 5-D model. Ostendorf, however, expressly included ability adjectives; consequently, his Factor V is a clear intellect factor defined by such terms.
In our Dutch lexical project, subjects were asked whether an adjective would fit in the framing sentence “he/she is [adjective] by nature” (cf. Brokken, 1978) in order to determine an adjective’s prototypicality as a trait descriptor.Adjectives like dull, gifted, capable, brilliant, one-sided, idiotic, sharp, and ingenious received very low prototypicality ratings (along with other categories of terms, most notably socialeffectadjectiveslikehorrible,commonplace,andcaptivating). In a selection of terms used by De Raad (1992) to establish the replicability of the 5-D model in the Dutch language, terms with low prototypicality were excluded; consequently, no clear fifth factor appeared. In a Dutch-German-American comparison (Hofstee, Kiers, De Raad, Goldberg, & Ostendorf, 1997), the correspondence between theAmerican and German structures was higher than the match of either with the Dutch structure, especially with regard to Factor V.
Plagued with feelings of intellectual inferiority, we took drastic steps to better our lives. In constructing the item pool for the FFPI (Hendriks et al., 1999), we expressly added 266 intellect items over the 1,045 constructed to cover the five Dutch factors (see Hendriks, 1997, p. 19f). However, only two of these 266 were judged to be perfectly comprehensible by our students of lower professional education, who did not connect to words like reflect, analyze, and contemplate. In a PCA of the whole item pool, based on responses of more sophisticated subjects, typical intellect items like Thinks ahead, Uses his/her brains, Sees through problems, Learns quickly, Is well-informed, and their counterparts had sizable secondary or even primary loadings on Factor III, conscientiousness; pure markers of V() were items like Follows the crowd, Copies others, and Does what others do. Consequently, Factor V() was interpreted as autonomy. We were thus unsuccessful in our attempts to arrive at an intellect factor. The autonomy interpretation of Factor V reappears in Italian data (see De Raad, Perugini, & Szirmák, 1997).
A powerful competitor—if only by virtue of the widespread use of the NEO-PI-R (Costa & McCrae, 1992)—to the intellect conception of Factor V is its interpretation as openness to experience. That construct does not come out of the lexical approach; in fact, McCrae (1990, 1994) has used it repeatedly to argue the deficiency of that approach. The consequent problem with such constructs, however, is that they do not share the taxonomic status that is awarded by the lexical paradigm. Furthermore, many of the NEO items in general, and of the openness to experience scales in particular, would not pass the comprehensibility test that was outlined earlier. Brand (1994) predicted that both intellect and openness to experience would correlate substantially with measured intelligence (g) over the whole intellectual range of the population. A special reason may be that subjects of modest IQ would reject such items because they do not understand them, and thus receive low scores.
Distinguishing Personality from Ability
The 5-D model seems to have contributed to a shifting emphasis from a narrow to a broad conception of personality. That shift can hardly be objected to as such. Not only are both intelligence and other personality traits stable and psychologically relevant, but they also combine with each other. An intelligent extravert may be found eloquent; a dull one may be judged to be loudmouthed. In the study on 5-D profiles of prototypical personality disorders (Hofstee, 1999) referred to earlier, the narcissistic and antisocial profiles were relatively close together, but that must be because the FFPI’s Factor V has little to do with intellect: Sizable differences between the two would be expected on measured intelligence (Millon, personal communication, September 29, 1999). For a proper assessment of personality, the inclusion of intelligence is indispensable.
There is no good reason, however, to contaminate typical behavior and maximum performance. On the contrary, there are good reasons to separate the operations. One is that objective measurement of intelligence is more scientific than its assessment, however intersubjective that assessment may be. Another is that methods are not neutral: Abilities and tests of maximum performance are as closely associated as are stylistic traits and assessments of typical behavior. To include ability items in questionnaires can only obscure the view on intelligence.
With respect to concepts of temperament and character, state-of-the-art assessment would include a 5-D questionnaire as a baseline instrument, and novel concepts would have to prove their added value against that background. According to the same principle of parsimony, however, 5-D factors have to prove their added value over measured intelligence. Precisely because personality and intelligence belong together, objective measures of intelligence should be included in investigating the structure of personality. In view of the scientific primacy of intelligence, its variance should be partialled out of the questionnaire scores. While in the process, attitudinal factors, which are out of bounds in most definitions of personality, should be removed in the same manner. They, too, are empirically correlated with certain versions of Factor V, particularly with openness to experience (Saucier, 2002a). With these corrections, it is entirely conceivable that little would remain of Factor V.
The Linear Approach to the Concept of Personality
The “Magical Number Five,” in the words of Goldberg (1992b), is intricately connected with applying PCA to large numbers of trait variables. Forerunners have been pinpointed, most notably Tupes and Christal’s (1961/1992) analyses. However, Tupes and Christal’s denomination of the fifth factor in terms of culture is now obsolete. On the other hand, if the magical number had been found to be six, one could have referred to another Cattellian’s (Pawlik, 1968) set consisting of I Extraversion, II Cooperativeness, III Deliberate Control, IV Emotionality, V Independence of Opinion, and VI Gefühlsbetontheit (which is difficult to translate; the order in which the factors appear has been adjusted to the present context). These examples of imperfect historical fit could easily be expanded upon. The five factors owe their consolidation and impact to analyses of large data matrices that did not become possible until the last decades of the twentieth century.
This section starts with setting out the strongest possible case for PCA by presenting a classical (see Horst, 1965) rationale for it. Next, it examines the grounds for the magical number five. It then considers the so-named person-centered approach as an alternative to PCA in certain contexts.
The Case for Principal Component Analysis
Applying PCA to a scores matrix is the logical consequence of performing item analysis. In the general case, the aim of item analysis is to maximize the internal consistency of one or more scales based on the items; the exception whereby items are weighted by their predictive validity is outside the present scope. The basic idea of item analysis may be expressed as follows: The investigator is aware that each single item, carefully chosen as it may be, is an imperfect operationalization of whatever construct it represents. But the investigator has no better criterion against which to gauge the validity of the item than the total score on the set of equivalent items. Item analysis is thus a bootstrapping operation.
Carrying this basic idea to its logical consequence proceeds as follows: At the first step, items are weighted according to their association with the total score. Discarding items on that basis would amount to arbitrarily assigning a zero weight. That may be defensible in extreme cases where it is evident for substantive reasons—albeit post hoc—that the item does not belong in the set. In the general case, however, all items would be retained.
By virtue of assigning weights to the items, however, the total score has been replaced by a weighted sum. The implicit rationale is that this weighted sum is a better approximation of the underlying construct than was the unweighted sum. So the logical second step would be to assign item weights according to their association with the weighted sum. Thus an iteration procedure has been started, the endpoint of which is reached when convergence of weights and of weighted sums occurs. At that point, the weighted total score is the first principal component of the item scores (Horst, 1965). If the item set is multidimensional, more than one principal component is obtained, but the reasoning is essentially the same.
Thus a particularly strong argument in favor of PCA is that it is logically inevitable. Also, since the days of computer scoring, any practical objections against calculating weighted sums have disappeared: Sooner than applying 10 hand-scoring keys to a 5-D questionnaire (five keys for positive items and five for negative items), one would put the item scores on electronic file anyway.
Raw-Scores PCA
The present argument does not prejudice in favor of PCA as it is usually conceived, namely, PCA of z scores or correlation matrices. Rather, it refers to raw-scores PCA, with deviation scores and their covariance matrices, or standardized scores and their correlations, as special cases. Raw-scores PCA should be performed on bipolar scores; for example, scores on a five-point scale should be coded as 2, 1, 0, 1, and 2: We (Hofstee, 1990; Hofstee & Hendriks, 1998; Hofstee, Ten Berge, & Hendriks, 1998) have argued that a bipolar representation of personality variables is appropriate, as they tend to come in pairs of opposites. Thinking in terms of all-positive numbers is a habit imported from the abilities and achievement domain, where it does not make sense to assign a negative score.
Raw-scores PCA implies an absolute-scale interpretation of the Likert scale, rather than the conventional interval-scale interpretation. These alternative interpretations have subtle consequences for our conception of personality. The first of these concerns the reference point. With relative, intervalscale scoring, the population mean is the reference point. For desirable traits, that reference point is at the positive side of the scale midpoint (0), and vice versa. Thus a person with a score of .8 on a socialness scale with a population mean of 1.1 (most people being found social), would be said to be somewhat asocial, albeit in a relative sense, which however is the only available interpretation when using interval scaling. The unthinking adoption of interval scales from the domain of intelligence and achievement may lead to a bleak view of humankind, whereby a sizable proportion of the population is judged more or less deviant. A poor comfort is that the proportion is a bit less than 50% because the raw-score distribution is not symmetric. Taking the scale midpoint seriously solves the problem; it prevents a positive judgment from being translated into something unfavorable and vice versa, based on an inappropriate convention.
The second way in which absolute and interval scale conceptions differ concerns spread. Using a five-point scale, most items have standard deviations close to 1, as the prevalent responses are 1 and 1; thus the difference between absolute and interval scaling is not dramatic in this respect. But extremely favorable and unfavorable items obtain smaller standard deviations. The effect of standard PCA and interval scoring procedures is to increase their impact on the total score. It would seem that this is also an unintended consequence rather than a deliberate effect.
In sum, item scoring through weights obtained by rawscores PCA deserves more consideration than it has received so far. The standard objection to treating scores on a Likert scale as absolute is that strong assumptions would be imposed on the data. I am unable to see the validity of that argument. So-called weak models may in fact be very strong: To assume that the midpoint of a personality scale has no meaning and, consequently, that respondents’evaluations can be reversed, is about as strong as hypothesizing, for example, that a large proportion of the population cannot be trusted. At the very least, the absolute conception of Likert-scale scores is no more indefensible than the interval conception.
A Review of the Grounds for the Number Five
Away to obtain many principal components is to analyze matrices with large numbers of variables, in this case single trait descriptors. Earlier, limitations on computing capacity virtually prevented the number of trait variables from being much larger than the 35 employed by Tupes and Christal (1961/ 1992). With the expanding power of computers, however, it became feasible to analyze the very large numbers of variables that were needed to justify claims of representativeness if not exhaustiveness. However, the sorcerer’s apprentice problem then becomes keeping the number of factors from getting out of hand. With hundreds of variables, it will take many factors to get down to the time-honored “eigenvalue 1” threshold; for example, the 20th factor in Ostendorf’s (1990) PCAof 430 traits still has an eigenvalue of 3.
Hofstee et al. (1998) proposed a more stringent criterion based on the alpha reliability of principal components, which is approximately 1 1/E with large numbers of variables, E being the eigenvalue of that principal component. Setting the minimum alpha at .75, an “eigenvalue 4” threshold results (E = 1 gives = 0). Using this criterion, Ostendorf (1990) should still have set the dimensionality of the personality sphere at about 14 rather than 5; with even larger numbers of traits, the dimensionality would only increase. There can be no doubt that the 5-D model discards linear composites of traits that are of sufficient internal consistency, and would add to the number of dimensions. It is of interest to note that the most prominent 5-D questionnaire, Costa and McCrae’s (1992) NEO-PI-R, in fact postulates 30 dimensions rather than 5, as each of the 30 subscales is deemed to have specific variance in their hierarchical model. (The five second-order factors do not add to the dimensionality, as they are linear combinations of six subscales at a time.)
An entirely valid pragmatic reason to restrict the number of factors is parsimony. The first principal component is the linear combination of traits that explains a maximum of variance; the second maximizes the explained variance in the residual, and so on. Consecutive factors thus follow the law of diminishing returns. Next, the scree test acts on the amount of drop in eigenvalue between consecutive factors; it thus signals points of increasingly diminishing returns. Using the scree test, Brokken (1978) retained 6 principal components in a set of 1,203 trait adjectives; Ostendorf (1990) retained 5. However, the scree test does not offer a unique solution; Ostendorf, for example, could have opted for an 8-factor solution on that basis. Neither PCA nor the scree test dictates the number of five.
Does replicability of factors provide a cogent criterion for the dimensionality of the space? That depends on how the term is understood. If one and the same large trait list were administered to large samples from the same population, the number of replicable factors would in all likelihood exceed five.At the other extreme, when independent, “emic” replications of the lexical approach in different languages are undertaken, the number tends to be in the order of three (De Raad et al., 1997; Saucier et al., 2000) rather than five, Ostendorf’s replication being an exception. Saucier, Hampson, and Goldberg list 18 points on which such studies might diverge and recommend methodological standardization. A familiar objection is that standardization leads to premature closure of the issue: Not only would the outcome depend on arbitrary choices, but moreover one could not tell anymore what makes a difference and what does not. It would be preferable to use these points for studies on whether and how the number varies in function of differences in approach.
In sum, the number five takes on the character of a point estimate in a Bayesian credibility function on an abscissa that runs from 0 to some fairly large number, with the bulk of the density stacked up between 3 and 7. As with other empirical constants, the uncertainty does not so much result from random error as from the interplay of diverging arguments and specifications. In any case, the number should be taken with a grain of salt.
The Person-Centered or Typological Approach
A familiar critique of trait psychology is that it loses the individual from sight (see, e.g., Block, 1995; Magnusson, 1992). Aset of alternative operations is available under labels such as type or person-centered approach; it comprises Q-sorts in preference to Likert scales, longitudinal designs to assess the dynamics of personality, and cluster analysis of persons rather than PCA of variables. Recent empirical studies (e.g., Asendorpf & Van Aken, 1999; Robins, John, Caspi, Moffit, & Stouthamer-Loeber, 1996) concentrate on the three “Block” types: resilient, overcontrolled, and undercontrolled. I document the relativeness of the opposition between the person-centered and variable-centered paradigms (see also Millon, 1990) but try to do justice to a real difference in their ranges of application.
Persons in Principal Component Analysis
Unlike factor analysis proper, in which factor scores are hardly more than an afterthought, PCA offers a fairly symmetric treatment of individuals and variables. One could rotate a matrix of scores on principal components to simple structure and characterize individuals by the person factor on which they had their highest score. In an even closer approximation to the person-centered approach, factors and loadings may be rescaled such that individuals receive loadings and variables receive factor scores. That is not precisely the same thing as performing Q-factor analysis, as the scores still become standardized per variable instead of per individual as in Q-analysis; but the two operations would be mathematically identical in the case of raw-score PCA. If the argument in favor of raw-score PCA is accepted, the difference between variable-centered and person-centered analysis reduces to a set of scaling constants and rotation criteria being applied to one matrix rather than another, which is hard to get excited about.
Variables and Types
An orthodox typological solution may be viewed as a binary matrix of persons by types with one 1 per row, representing the type to which that person is assigned, and 0 scores in the remaining cells. At the other extreme, each person could be given a score for each type on a continuous scale, representing the extent to which that person corresponds with that type, thereby treating the types as continuous variables. The orthodox solution could be reconstructed from that matrix by selecting the highest score per row and dichotomizing accordingly. Intermediate, liberalized typological solutions (Millon, 1990) could also be derived, most notably through matrix-wise dichotomization of the continuous scores. In the liberalized solution, some persons would appear to be assigned to more than one type, whereas some others would fail to meet the threshold for any type at all. The types would no longer be orthogonal in the way they are forced to be according to the orthodox solution; so one could correlate the types, factor analyze them, and the like.
To those who would find this methodological play with types improper, there is a perfectly serious answer. In the ideal case, a diagnosis is performed by an infinite number of independent experts. Experts do not agree perfectly in all cases.
Thus the sum or average of even their orthodox typological solutions would give precisely the kind of matrix of continuous scores introduced in the earlier argument. In a scientific (in the sense of intersubjective) conception of types, the continuous matrix is the primitive case, not the binary matrix.The primitive case arises not because types (or even personality variables in general) are necessarily continuous as such, but because of the tacit third dimension of the matrix.
Q-Sorts and Likert Scales
Investigators working in the person-centered paradigm prefer ipsative scores, as they would represent intra-individual rather than interindividual comparisons. Varieties of ipsative scoring are row standardization, which fixes the means and standard deviations, and forced distribution, whereby all moments are fixed. Q-sorts automatically result in forceddistribution scores (unless the number of items in the “most applicable” to “least applicable” categories is not fixed, in which case, however, the method is indistinguishable from using a Likert scale).
Like orthodox typologies, ipsative scores may be constructed from continuous “interactive” scores, in this case by standardizing over variables or by forcing a distribution on them. One might object that Q-sorts are different in principle from Likert-scale scores, but that remains to be seen. In the first place, judges need not respond the way we instruct them to. If I am asked, by way of intra-individual comparison, whether I am (or John is) more reliable than friendly, I may well respond against the background of people in general; it could even be argued that the question is meaningless without that background. Conversely, when confronted with a standard personality questionnaire, intra-individual considerations might well enter into my response process. It is thus arguable that all responding is interactive. In the second place, Q-sorts are used to compare people, therefore, interindividually: If John is said to be of Type A whereas Mary is not, the intra-individual level is automatically surpassed.
The effect of ipsatization is to remove interindividual differences in elevation and spread (and skewness, kurtosis, and so on) of the responses. The operation thus implies a view of personality in which such individual differences have no place. Surprisingly, that view appears to be shared by some unadulterated trait researchers, most notably Goldberg (1992a) and Saucier (1992; see, however, Saucier, 2002a). Their rationale, however, has nothing to do with an emphasis on intra-individual differences. Rather, they use ipsatization of Likert-scale data to remove differences in scale usage, in other words, response sets. Whatever the rationale is, the implication needs to be examined in detail.
Removing differences in elevation and spread prevents one person from having more traits than another, as well as from being more extreme. Correcting for elevation is quite defensible in the specialcase where the variable setis completely balanced (i.e., consists of opposites like reliable and unreliable). Except in a fairly poetic manner, it hardly makes sense for a person to be both more X and un-X than another; it is more parsimonious to attribute such a response pattern to excentric scale use, traditionally denoted as the acquiescent response set. Hofstee et al. (1998; see also Ten Berge, 1999) presented ways to correct for excentric responding.However, if thevariables set is not balanced, correcting for elevation removes content and social desirability variance. In the most elementary case, John is prevented from being both more friendly and reliable than Mary. That consequence is infelicitous.
The person-centered approach is thus subject to an irony of fate: An intention (a proper approach to personality) materializes into an operation (ipsative scoring) that appears to cradle aversive implications (for the very concept of personality). Ipsatization would do the job in a strictly idiographic approach, but that condition is not fulfilled: By virtue of the fact that one and the same method and vocabulary is applied to more than one person, interindividual comparison automatically creeps in. It may make sense to separate ipsative and normative components of a scores matrix by representing the latter as a vector containing the person means. Discarding that vector, however, has the effect of flattening the concept of personality. Essentially the same argument applies to individual differences in spread (and other moments of the score distribution).
Dynamics
Analytically, a dynamic approach to personality, as advocated by person-centered investigators, may mean either of two things: taking the time or growth dimension into account, and interpreting traits as an intra-individual pattern, therefore, in a nonlinear fashion. The dynamic approach thus stands in opposition to an orthodox trait approach, which is static and linear.
However, dynamics are easily accommodated in the individual-differences paradigm. A chronological series of assessments pertaining to an individual may be conceived as an extension of the scores vector. In a multiple prediction of some criterion, the question then becomes whether, for example, last year’s emotional stability has incremental validity over today’s. Alternatively, a (fitted) growth curve may be represented by its first derivative representing growth speed, its second derivative representing growth acceleration, and so on, in addition to the overall score of that individual.
Again, the derivatives function as extra traits. Similarly, pattern interpretation may be represented by introducing extra predictors, in this case, moderator or interaction terms formed by multiplication of predictors. Thoroughbred trait psychologists would argue that growth and pattern scores cannot be expected to have incremental validity, but that is not an objection of principle. What this brief analysis shows is that the two paradigms are not ideologically incompatible but appear to consist of different generalized expectations regarding the relevance of growth and moderator terms.
A final wording of the moderator issue is whether single predictors may receive different weights according to the individual in question; thus, whether Mary’s emotional stability may be less relevant in predicting her performance as a pursuit plane pilot than is John’s. Again, there is no a priori reason whytheweightsshouldbeuniform.Atechnicalproblemisthat the Pearson correlation is undefined in the single case; however, raw-score association coefficients like Gower’s (1971) and Zegers andTen Berge’s (1985) can do the job.Their application to the single case also gives a precise expression to the otherwise elusive idea of intra-individual trait structure. The Gower coefficient for the general case is the mean of the single-case coefficients; it thus writes interindividual structure as the mean of intra-individual structures, thereby joining two paradigms of personality that are usually brought in opposition to each other. This integration is still another reason for taking raw scores seriously. An empirical problem, however, is that individual weights may be extremely unstable. However, the same holds for intra-individual structure.
Ranges of Application
After digesting a number of red herrings, what remains is a matter of conventional preference. The trait psychologist represents the person as a vector of scores on a continuous scale, whereas the typologist would prefer a single qualification on a binary (applicable vs. not applicable) scale. Taking a sophisticated trait model incorporating growth and moderator effects, the person-centered approach is a special or degenerate case of it, and can therefore not be psychometrically superior in any respect. To justify the type approach, a different perspective should be adopted. To that end, I distinguish between a context of prediction and a context of communication.
Given the same basic materials, there can be no reasonable doubt that the trait approach is superior in a predictive context. On the one hand, typing consists of discarding information that is potentially valid. On the other, it introduces dynamic predictor terms whose empirical status is highly dubious; therefore, even an orthodox trait approach may be expected to do better upon cross validation.
Ironically, the 5-D approach meets with ambivalence from the side of its very proponents in predictive respects. McCrae and Costa (1992) and Jang and others (1998) have emphasized the incremental validity of the 30 subscales of the NEO-PI-R (Costa & McCrae, 1992) over its five factor scales, thereby implicitly questioning the 5-D model as an adequate representation of personality. The psychometric value of such arguments, however, is quite limited. Principle component analysis capitalizes on the common variance in the predictor set; successive residuals follow the law of diminishing returns. So does validity, unless in some magical and unintended way specific variance would be more valid than common variance.
The value of the type approach is to be found at a different, pragmatic level, at which personality is a subject of communication between a diagnostician and a therapist (in the wide sense of someone who is going to work with the individual, possibly the individual him- or herself). Human discourse and cognition being what they are, it makes little sense in that context to exchange vectors of continuous scores. Professional communication is better served by an attempt to capture the essence of the individual’s personality in a vivid and suggestive picture. To insist on using a trait paradigm in this context is to ignore the human element at the receiving end of a communication.
In the end, the two sets of operations appear to refer to different conceptions of personality-in-context rather than personality-in-vitro. The trait approach is geared toward automated predictive procedures in which substantive considerations do not even surface. The type approach caters to human receivers of personality information. Which of the two scripts is appropriate in a particular case is difficult to say in abstract terms. A personnel selection situation, for example, may be conceived in predictive as well as in communicative terms; the same goes for a clinical intake situation. The emphasis here is on distinguishing the scripts: Predicting on the basis of types and communicating in terms of traits are both arguably deficient.
Hierarchical and Circumplex Structures
In a hierarchical model, trait concepts are seen as specifications of broader traits, which in turn may be grouped under the heading of supertraits. In a circumplex model, trait variables appear as combinations of each other; they form a network in which all concepts define each other in a recursive manner, without subordination or superordination. In mixed models, all variables and factors are equal, but some are more equal than others because they explain more variance or are assigned privileged status for conventional reasons.
This section contains an evaluation of trait taxonomies that have been proposed or implied, and it works its way toward a family model that may be acceptable by way of integration. However, it should be kept in mind that taxonomies are subject to contradictory demands, namely, conceptual and communicative simplicity on the one hand, and adequate coverage of empirical reality on the other.
The Principal Component Analysis Plus Varimax Taxonomic Model
In its elementary form, the Big Five structure consists of a varimax rotation of the first five principal components taken from a large heterogeneous set of trait adjectives (see, e.g., Ostendorf, 1990). Whether this result is intended as a model in any proper sense is irrelevant, as it evidently functions like one: People receive scores on the Big Five, and these scores are interpreted as their personality structure—specifically, an orthogonal structure according to which these factors vary independently over persons.
Goldberg (1993a) articulated that the model in question may be viewed as hierarchical: Items specify scales, and scales specify factors. This argument presupposes simple structure, but that condition is not fulfilled. A concomitant and very widespread notion is that the Big Five are “broad” (in the sense of fuzzy) factors of personality.
The Implicit Assumption of Simple Structure
Simple structure, in which each variable loads on only one factor and factors exhaust the common variance would be hierarchical indeed: Each variable would be a specification of only that factor; a particular factor could legitimately and meaningfully be interpreted in terms of the variables that load on it. The interpretation would not surreptitiously introduce other variance common to some subset of the variables in question.
In empirical practice, however, variable structures are so overwhelmingly complex—as opposed to simple—that the hierarchical model functions as an obstacle to proper conceptualization: The practice of interpreting factors on the basis of their highest loading items, which would be appropriate under simple structure, is quite erroneous if the condition is not fulfilled. For to the extent that some of the highest loading items share other common variance, factor interpretations become contaminated. For example, an extraversion factor easily receives a social interpretation (sociability, social extraversion, and the like; for an overview, see Digman, 1990)
because many high-loading items have positive secondary loadings on agreeableness.
The Alleged Broadness of Factors
Under conditions of actual simple structure, factors could be called broad in a hierarchical sense, as they capture the common variance of a number of variables. Even then, factors are not broad in a conceptual sense but rather more narrow than variables, as their internal consistency is higher and their angular position in the trait space is thus more fixed. A g factor of intelligence, for example, is not a broadband but a highfidelity measure of some latent trait. A fortiori, there is nothing broad about a Big Five factor based on a particular domain of trait variables. For lack of actual simple structure, it does not encompass a sizable number of lower level items or scales. The meaning of a factor, even if latent, is much more precise in a psychometric sense than is the meaning of the variables on which it is based. In that domain of variables, a set of five rotated principal components covers more variance than does any other set of five linear combinations, but “broadness” is an inappropriate and misleading term for that.
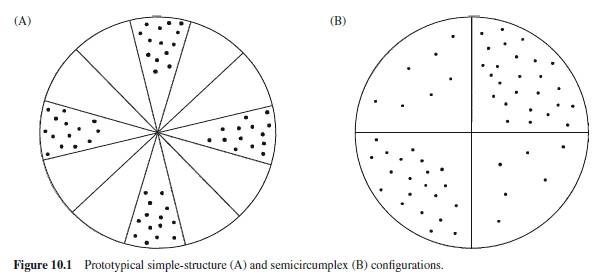
In another terminology, to view the Big Five as broad factors is to treat them as a circumplex structure. In a regular two-dimensional circumplex, the plane is sliced into a number of angular segments (e.g., 12 segments). Variables within a segment form a homogeneous set. A special case is simple structure, in which “mixed” segments are empty, as in Figure 10.1, panel A. The actual situation, however, is closer to panel B, amounting to a circumplex with four segments, of which two are well filled. These segments contain very heterogeneous sets of variables; two of those variables may even be orthogonal to each other. The very specific meaning of the factor is thus not adequately captured by the broad array of variables that have their primary loading on it.
Marker Variables
The interpretation problem would be solved if stable marker variables could be found, that is, trait terms that load exclusively on one factor. Goldberg (1992a) presented such sets of psychometric synonyms, for example, extraverted, talkative, assertive, verbal, bold, and five other terms for the positive pole of the extraversion factor. A minor problem with this interpretation strategy is that markers for some factor poles are difficult to find, for example, markers for emotional stability. A major problem is that marker sets appear to be no longer orthogonal in fresh samples or upon translation. Any two homogeneous sets of traits may be expected to correlate positively if both are desirable or if both are undesirable, negatively if they are opposite in that respect; neutral sets hardly exist. Orthogonal sets may be selected in a sample, but they will regress to obliqueness upon cross validation. On the basis of a large-scale study, Saucier (2002b) has developed marker scales that appear to be robustly orthogonal within his several data sets and might thus defy the present analysis. Still, one would have to wait and see how they do in another laboratory, for example, when transported abroad.
The obliqueness problem (see, e.g., Block, 1995) cannot be answered by the truism that varimax-rotated factors are by definition orthogonal. The missed point is that they have no interpretation—not because they are broad or fuzzy, but because any interpretation in terms of sets of variables is biased. To interpret a Big Five factor properly, one would have to perform and communicate a suppression operation, such as the following: Factor I is what remains of extraversion after suppressing any connotation of agreeableness or socialness that may be associated with it, however firmly; Factor V is a residue of intellect or openness to experience after subtracting a virtually indissoluble tinge of energy, which rather belongs to Factor I. That is a bit much to ask.
In conclusion, the PCA plus varimax set of operations leads to an inadequate representation of personality. The argument is not that traits are correlated, in any metaphysical sense: For purely predictive purposes, linear regression of criteria on orthogonal factors is a perfectly defensible approach. What was stressed is the conceptual risk of starting to talk in Big Five terms, either among experts or with others. Conceivably, we could keep our mouths shut, but in practice that is too high a price to pay.
The PCA plus varimax model has been imported into personality from the domain of intelligence research. The question arises whether it is appropriate in that domain. I (Hofstee, 1994c) have argued that it is not. The empirical structure of intelligence variables is an n-dimensional simplex (the all-positive quadrant of an n-dimensional sphere) characterized by positive manifold and lack of simple structure. Treating it as an orthogonal simple structure gives rise to biased conceptualizations of the underlying dimensions and inadequate representation of the domain. Essentially the same objection holds for the domain of personality.
The Double Cone Model
Aseminal attempt at a specific structure model of personality in the 5-D framework is Peabody and Goldberg’s (1989) double cone, based on Peabody’s (1984; see also De Boeck, 1978) work on separating descriptive and evaluative aspects of trait terms. It focuses on the first three Factors; the smaller factors IV, emotional stability, and V, intellect, are treated as separate axes orthogonal to the sphere that is formed by the bigger three: I Extraversion, II Agreeableness, and III Conscientiousness.
The double cone model may be envisaged as follows: Take a globe with desirability as its north-south axis, so that all desirable traits are on the northern hemisphere and their undesirables opposites are on the southern hemisphere in the antipode positions. Apply an orthogonal rotation to the Factors I, II, and III such that their angular distances to the desirability axis become equal, namely, 54.7 deg with cosine 1/3. Draw a parallel of latitude at 35.3 deg (close to Kyoto and Oklahoma City) through the positive endpoints of the Factors I, II, and III, and another one (close to Sydney and Montevideo) through the negative endpoints. Connect each possible pair of antipode points on the two circles by a vector. Together, these vectors form the double cone. The model represents empirical trait variables by their projection on the closest model vector.
The double cone was designed to embody a particular taxonomic principle, informally referred to by insiders as the Peabody plot and named chiasmic structure by Hofstee and Arends (1994). A classical example of a chiasm is
Thrifty Generous
Stingy Extravagant
In Peabody’s reasoning, this configuration arises by pitting a content contrast (i.e., not spending vs. spending) against a social desirability contrast (thrifty and generous vs. stingy and extravagant). In the double cone model, chiasmic structure recurs in the shape of Xs that are formed by vertical slicings through the center of the double cone. On the Northern circle, we would have thrifty and generous at opposite longitudes; on the southern hemisphere, stingy and extravagant. More generally, descriptive and evaluative aspects are represented by longitude and latitude, respectively.
Evaluation of the Double Cone Model
The model is readily generalized to five dimensions, although it loses some of its aesthetic appeal in the process: Take all 10 subsets of 3 out of the 5 factors, that is, the I II III, I II IV, through III IV V subsets, and treat each of these spheres in the manner just sketched. The generalized double cone thus consists of a Gordian knot of 10 three-dimensional double cones in the 5-D space sharing their vertical (desirability) axis, or 10 pairs of latitude circles. There is no valid reason why the range of the chiasmic structural principle should be restricted to a particular subset of three dimensions. But the model easily passes the generalizability test.
It is not entirely clear whether the algorithm for analyzing the data as used by Peabody and Goldberg (1989) is consistent with the model. Via Peabody (1984), the reader is referred to an algorithm proposed by De Boeck (1978). De Boeck’s procedure, however, sets the I, II, and III dimensions orthogonal to the desirability axis, rather than at 54.7 deg. Still, it is certainly possible to design an algorithm that would be consistent with the double-cone model.
The next question, however, concerns fit. That may be tested by assessing the quality of chiasms that are generated by the model. Hofstee and Arends (1994, Table 1) present chiasms derived from Peabody and Goldberg’s (1989) materials. An example is
Forceful Peaceful
Quarrelsome Submissive
The content contrasts in this and in other examples are not convincing. The reasons are not hard to find. First and most important, the cone structure supposes an angular distance of only 109.5 deg between terms that should form a content contrast, like forceful-peaceful and quarrelsome-submissive. Second, 5-D factors have different angles with the desirability vertical axis: II, agreeableness, for example, is much further north than is I, extraversion. When these angular distances are forced to be equal, as in the model, content contrasts become contaminated by a desirability contrast. In the example, peaceful is more desirable than forceful; therefore, to the extent that they are at all judged opposite, that is partly an artifact of a desirability difference.
It is fair to conclude that the double cone does not model the underlying principle of chiasmic structure in an optimal way. One could refine the model, but there is no need to do so: Hofstee and Arends (1994) showed that the Abridged Big Five circumplex (AB5C; see Hofstee, De Raad, & Goldberg, 1992) model to be discussed later can account for chiasmic structure, and generates credible chiasms:
Daring Cautious
Reckless Timid
In two experiments, participants judged content contrasts taken from AB5C chiasms to be superior over double cone contrasts. This is not to say that chiasmic structure exists: Hofstee and Arends reiterate a point already taken by Peabody (1967) himself, namely, that desirability and content cannot be separated. So the best one can do is create a chiasmic illusion, as in the previous example. The algorithm goes as follows: Take a particular circumplex; draw a diameter separating desirable from undesirable traits; select two traits on different sides of the diameter but close to it and to each other, for example, cautious (slightly desirable) and timid (slightly undesirable); together with their opposites, they create the chiasmic illusion. It arises because in this case the alleged content contrast is formed by two terms with an angular distance that is only slightly less than 180 deg, instead of 109.5 deg as according to the double cone model.
Do Chiasms Have a Future?
The double cone model was shown to be generalizable; it may be possible to design a refined version by widening the angle between content opposites, amounting to oblique rotation. The more basic questions that remain, are What is the taxonomic status of the underlying principle of chiasmic structure? and What does it do to our conception of personality?
Whatever the refined model would be, it would focus on traits that are close to the equator of a hypersphere whose vertical axis is desirability: The model would focus on fairly neutral traits. They form a small minority, so the focus would be on a counterrepresentative subset of personality variables. On the one hand, there is something venerable (to use Saucier’s, 1994, term) to such a value-free approach; personality psychologists, like everybody else, would prefer practicing a discipline that is not submerged in extrascientific values. On the other, desirability is not fruitfully considered as a mere response set or other artifact that is to be separated from content: Hofstee and Arends (1994) emphasized that even in the classical example of chiasmic structure cited earlier, stinginess is not merely undesirable thrift, but an asocial version of it, whereas generousness differs from extravagance in being prosocial; therefore, the evaluation contrast is in fact one of content, as in the AB5C model. So the most realistic conclusion is that chiasmic structure and related models cannot be central to the concept of personality, even though they may have their place in specific contexts (see Saucier, 1994; Saucier, Ostendorf, & Peabody, 2001).
Central features of the double cone model, however, appear to be valuable by themselves. One is the “circular pattern” (Peabody & Goldberg, 1989, p. 556), as opposed to simple structure, that is embodied in the model. Another is orienting the trait space toward desirability as its reference axis. These points are taken up later when developing an integrative family of structure models.
Generalized Circumplexes
In circumplex models, traits are assigned to segments of a circle and are thus represented by their projection on the bisectrix of that segment. Circumplexes picture tissues or networks of traits: Contrary to hierarchies, circumplexes have no superordinate and subordinate concepts. Eysenck and Rachman (1965), for example, represented Hippocrates’ melancholic, choleric, sanguinic, and phlegmatic types as mixtures of the positive and negative poles of neuroticism and extraversion; presumably, however, Hippocrates would have preferred a rotation by which an extravert is a mixture of the choleric and sanguinic types, neuroticism is what melancholics and cholerics have in common, and so on. Circles enjoy full freedom of rotation.
Circles generalize to spheres, and spheres generalize to hyperspheres—particularly, in this context, to the 5-D hypersphere. An early example of a 3-D structure is Heymans’s (1929) temperament cube. Not until the end of the twentieth century, however, did 5-D researchers (Hofstee et al., 1992; Saucier, 1992) construct circumplexes of more than two dimensions.
Heymans’s Cube
Heymans (1929) constructed a network model with three dimensions—emotionality,primaryversussecondaryfunction (comparable to extraversion-introversion), and activity— forming the axes of a cube. Types are located at each of the eight vertices of the cube, among which are the four Hippocratic types; for example, the sanguinic type is at the vertex where low emotionality, primary function, and high activity meet.
Heymans tended to conceive the temperament space as unipolar: The type characterized by the absence of emotionality, activity, and secondary function is named amorphous. One amendment therefore is to move the origin of the trait space to the center of the cube. Next, it is difficult to conceive of activity and primary function as orthogonal; different dimensions (and types) would be chosen in a contemporary three-dimensional model. Finally, one would prefer rounding the cube to a sphere. On the one hand, it is thus gratifying to note that time has not stood still, and that Heymans’s cube is now obsolete by reasonable standards. On the other, it is equally gratifying to recognize Heymans’s model as a forerunner of the generalized circumplexes that did not appear until the end of the twentieth century.
Saucier’s Rhombicuboctahedron
Saucier (1992) presented an integration of interpersonal and mood circumplexes and the Big Five Factors I, II, and IV. He drew attention to the fact that simple structure does not materialize in these domains; many variables are interstitial in that they are closer to the bisectrix of the angle between two factors than to the factors themselves. When simple structure is nonetheless imposed, interstitial variables are likely to be assigned to different factors by different investigators, even though the positions of variables and factors are closely comparable. Saucier constructed 6 bipolar scales as benchmarks for the interstitial positions, in addition to the 3 bipolar factor markers: a III versus III scale (friendly vs. unfriendly), a III versus III scale (dominant vs. submissive), and so on. He depicted the resulting trait structure as a rhombicuboctahedron, a prism showing the 18 (i.e., 2 [3 6]) unipolar benchmarks as facets.
Saucier’s model may be alternatively conceived as an abridged three-dimensional circumplex, depicted by three orthogonal circles based on two of the three factors at a time. Each circle contains two bisectrices of the angles between the factor axes; in the model, a variable is represented by its projection on the vector (out of 9 bipolar or 18 unipolar vectors) to which it is closest. This representation has the advantage that it is easily carried to the fifth dimension (discussed later). Saucier showed that the I II IV sphere was the most interstitially structured of all 10 spheres that are contained in the 5-D hypersphere; that difference, however, is quite relative in view of the many mixtures involving Factors III or V.
Like Wiggins’s (1980) two-dimensional interpersonal circumplex, Saucier’s model uses octants, which are 45 deg wide, corresponding to a correlation of .707. Therefore, the variables assigned to such a segment may still form a fairly heterogeneous set. Hofstee et al. (1992) distinguished traits that had their primary loading on one factor and their secondary loading on another (e.g., III; sociable, social) and traits with a reverse pattern (III; merry, cheerful). This strategy amounts to slicing up a circle into 12 clock segments of 30 deg, corresponding to a correlation of .866. Areason for making these finer distinctions is that 30 deg is about the angular distance at which vectors are still given the same substantive interpretation (Haven & Ten Berge, 1977). If this amendment is worked into Saucier’s model, it becomes identical to a three-dimensional version of the abridged circumplex.
The Abridged Big Five Circumplex Model
The AB5C model consists of the 10 circumplex planes that are based on 2 of the 5 factors at a time. Thus, variables are represented by their projections on the closest plane or, more precisely, on the closest of the 6 bipolar clock vectors (running from 12 o’clock to 6 o’clock, 1 to 7, and so on) in that plane. The hypersphere contains large empty spaces between the model planes, so it may look as if the abridgement is rather drastic. However, varimax rotation puts the variables as close to the planes as possible; Hofstee et al. (1992) showed that it does a better job at this than at maximizing simple structure, which is putting the variables as close to the single factors as possible. Thus, representing traits by their two highest loadings seems acceptable; a model including tertiary loadings is entirely conceivable, but it would be much more complex and add very little.
More aptly than by a spatial configuration, the AB5C tissue is depicted by a table using the 10 factor poles (I, I, II, II, and so on) as both warp and weft, the column denoting the primary loading, and the row, the secondary loading of the traits assigned to a cell. Of the 100 cells in that table, the 10 combinations of the positive and negative poles of the same factor are void; the remaining 90 contain the unipolar facets generated by the model. The gain over the simplestructure model is enormous. That model accommodates only relatively pure factor markers, that is, traits assigned to the 10 diagonal (II to VV) cells of the table. If simple structure would in fact materialize, most if not all of the variables would be found in those cells. If, on the other hand, the empirical structure is essentially circumplex, only 11.1% of the variables would find their way to the diagonal cells. In Hendriks’s (1997) analysis of 914 items, 105 (11.5%) ended up in those cells. That illustration is as dramatic as is the percentage of variables that would have to be discarded in a proper application of the simple-structure model.
In the discussion of the person-centered approach, I introduced a distinction between the contexts of prediction and communication. Against that background, it should be noted that the predictive gain of the off-diagonal AB5C facets over the five principal components is nil, as the facets are linear combinations of the components. However, they do serve conceptual, interpretive, and communicative purposes. An individual’s profile of scores on the FFPI, for example, may be typified by that person’s single most characteristic facet; thus, for example, a person whose highest score is on factor V and whose second highest score is on III may be characterized by the cluster of expressions and adjectives that form the VIII facet (Knows what he/she is talking about, Uses his/her brains, Sees through problems, and the many other items listed by Hendriks, 1997, for this “Tight Intelligence” facet). One or more of these catch phrases should be more effective than presenting a 5-D profile or even the subset based on the scores in question (“This person is primarily someone who Thinks quickly [V], and secondarily someone who Does things according to plan [III]”). Furthermore, at the theoretical level the AB5C model accounts for a large number of concepts that do not coincide with the five Factors but are quite adequately reconstructed as their mixtures.
Another way to document the flexibility of the AB5C design is in noting that it incorporates features of both oblique rotation and cluster analysis on an orthogonal basis. Oblique rotation as such does not solve the simple-structure problem when the configuration of variables is essentially circumplex. However, the insertion of oblique model vectors enables one to capture relatively homogeneous clusters of traits. That function is also served by cluster analysis procedures, but they lose sight of the dimensional fabric of the structure and the recursive definitions of clusters.
With respect to predictive purposes, the loss incurred by adopting the AB5C model is quite limited. First, the principal components base maximizes the internal consistency of the facets (Ten Berge & Hofstee, 1999), which should be beneficial to their validity. Second, if factors beyond the Big Five are needed to increase validity, the model is easily extended to include those factors. That would be more efficient than including separate scales for each additional specific concept.
Undoing Hierarchies
The traditional design of questionnaires is hierarchical: Items are grouped into subscales, subscales into scales. From the manuals of such questionnaires (see, e.g., Costa & McCrae, 1992) it is easily verified that subscales actually form a network; they have substantial secondary correlations with scales other than the one they are assigned to. Upon analyzing the single items of a questionnaire, a similar tissue pattern would arise; items would appear to have all sorts of promiscuous relationships, inviting circumplex analysis of the data.
Generalized (beyond two dimensions) circumplex analysis would proceed as follows: First, the item scores are subjected to PCA. The maximum number of principal components would be the number of subscales or facets (e.g., 30 in the case of the NEO-PI-R). Note that these 30 principal components extract more variance by definition than traditional scoring does. (In practice, it would soon become apparent that only a part of these principal components should be retained because the redundancies in the item tissue are captured by fewer components than the number of subscales.)
At the scale level, the optimal strategy is to proceed from the first m principal components, m being the number of superordinate scales (e.g., 5), as they make more efficient use of the data than do traditional scale scores. If, for reasons of continuity, the original interpretations of the scales are to be simulated, target rotations of the m principal components toward these scales could be carried out. If the original scales are conceived to be orthogonal, as in 5-D questionnaires, the optimal approximation procedure would be a simultaneous orthogonal target rotation of the m principal components towards the set of m scales. That procedure conserves internal consistency (Ten Berge & Hofstee, 1999); consequently, the average coefficient alpha of the rotated principal components is maximal. Most notably, it is automatically higher than the average alpha of the original scales.
Subscales of traditional questionnaires are very short; therefore, they are unreliable or consist of asking essentially the same question over and again, which is annoying to respondents and introduces unintended specific variance. If they are to be retained, their quality can be improved to a considerable extent by estimating subscale scores on the basis of (maximally) as many principal components as are postulated by the questionnaire model (e.g., 30). The procedure would consist of a target rotation of these principal components toward the subscale in question. Thus, using the collateral information contained in related items would generally increase the subscale’s internal consistency, even though the contribution of “bloated-specific” variance to it would be diluted, which in itself would be a desirable side effect.
The previous script, however, amounts to proving that the performance of a hierarchically conceived questionnaire can be boosted by placing a network model under its hood. Following the script would sooner or later lead to adopting the generalized circumplex approach, which implies a view of personality structure as a tissue rather than a hierarchy. At the superordinate scale level, one would hit upon a large number of interesting AB5C facets, which are linear combinations of the first m principal components; at the subscale level, a great amount of redundancy would be found, leading to a drastic reduction of the conceptual rank of the data matrix. The future of personality structure is hyperspheric.
Pruning the AB5C Model
The hypersphere of personality is riddled with gaps. Upon presenting the AB5C model, Hofstee et al. (1992) already noticed that its circumplexes were not evenly filled: The 1 o’clock versus 7 o’clock and 2 versus 8 segments attracted far more trait terms than did the 4 versus 10 and 5 versus 11 segments. The former segments contain consonant mixtures of either two positives factor poles (e.g., III, sociable) or two negative poles (e.g., III, unsociable), whereas the latter contain discords combining a positive and a negative pole (e.g., III, submissive, vs. III, dominant). The scarcity of discords reappears in Hendriks’s (1997, p. 45) results: Of the off-diagonal items, only 23% combine a positive and a negative factor pole, whereas the number of consonant and discordant cells is equal. Furthermore, discords tend to have the smaller projections in the 5-space, as may be verified from the cited studies. These results reflect the classical (e.g., Cruse, 1965) finding that neutral trait terms are scarce. The lexical axiom would imply that people find the corresponding behaviors relatively unimportant.
The rationale for introducing blends, in circumplex models in general and in theAB5C model in particular, is communicative. In the case of discords, the communicative benefits are unlikely to materialize. Rigid, for example, has a projection of .29 on the IIIII vector in theAB5C model (Hofstee et al., 1992, p. 157); unkind and orderly have projections of .52 on II and .67 on III, respectively. Thus, the projection of the weighted sum of unkind and orderly on the IIIII vector would be about twice as high as the projection of rigid itself. “John is primarily unkind and secondarily orderly” may thus be expected to communicate better than “John is rigid.” Therefore, the discordant hyperquadrants may be deleted from theAB5C model. It would thereby become semicircumplex: Of each circumplex, only the first and third quadrants would be retained. Clinicians, who tend to be sensitive to ambivalences of personality, might deplore that loss. However, the removal might well clarify intraprofessional communication, not to speak of communication with lay clients.
Extending this analysis would lead to a proposal for a somewhat different rotational positioning of the 5-D axes in order to maximize the coverage of consonant variables. In their present definition, some factors (notably, II and III) are associated more closely with desirability than are others (notably, I and IV). Thus, the vector in the I by II quadrant upon which the projections of the Desirability values of the traits would be maximal is closer to the II axis than to the I axis. This asymmetry is illustrated by the fact that an undesirable trait like unrestrained (at 2:30 on the clock) has a distance of only 30 deg from that bisectrix (which is at 1:30), whereas agreeable (at about 11:20) is more than 60 deg removed from it. Acounterclockwise rotation of the two factors would recognize unrestrained as a discord and agreeable as a consonant trait, which seems appropriate.
Applying this operation to all axes jointly amounts to a rotation to desirable manifold, mirrored by undesirable manifold. The resulting abridged Big Five semicircumplex (AB5SC) model is thus contained by the 10 faces of the hyperquadrant centered around the desirability axis and their 10 opposites. Each face is divided into three segments of 30 deg, placing the model vectors at clock positions of 12:30 versus 6:30, 1:30 versus 7:30, and 2:30 versus 8:30. (A more elegant representation involving a 45-deg counterclockwise rotation is presented later.) As no vectors recur in other semicircumplexes, there are now 30 bipolar model vectors.
In the following section the AB5SC model returns as a member of a family of models. That family comes about by a somewhat different rationale. The number five is no longer fixed; the emphasis shifts from 5-D models to accounts of trait structure that incorporate a number of principles that contribute to an efficient description of personality. Also, the factors as such disappear into the background, which is where they should have been from the start.
A Family Model of Trait Structure
What remained of hierarchical structure is the fact that each subsequent principal component explains less variance and is subordinate to its predecessors in that respect. The head of the trait pedigree is the first principal component, named the p factor of personality by Hofstee et al. (1998), in analogy to the g factor of intelligence, and in distinction to Eysenck’s (1992) psychoticism or P factor, which is intended as a lower level construct. A family of models may be constructed by adding one principal component at a time. Thus at the second level we have a circumplex or semi-circumplex; at the third a three-dimensional generalized one, and so on.
The Primordial One
In search of superlatives over the Big Five and the giant three (Eysenck, 1992), primordial appears as a good label for the p factor. That factor derives a mythical quality from its close association with desirability. It presents a fundamental paradox to students of personality, whose ultimate challenge is to manage the potent values that nourish its roots: Not until we are capable of giving an overall evaluation of an individual’s personality in a perfectly respectful manner will we have mastered that challenge.
In principle, there is nothing broad or vague about the p factor. Quite to the contrary, it is by definition the most internally consistent linear combination of all traits, explaining some 10% to 15% of the total variance in unselected item sets (see, e.g., Brokken, 1978; Hendriks, 1997; Ostendorf, 1990), just like the g factor does in the intelligence domain. In other words, no scale based on any subset of the items, however optimally weighted, is as internally consistent as p. Its location in the personality sphere is almost completely fixed in any large data set.
Fixing the interpretation of p across studies is another matter. In Hendriks’s (1997) unselected set of 914 items, p is best labeled as competence (Hofstee, 2001). In Saucier’s (2002a) study of representative sets of trait adjectives, it appears as a character factor taking in altruism, self-discipline, and success. The first principal component of the FFPI, whose 100 items were selected to cover the five factors equally, is an optimism factor (Hofstee et al., 1998). In view of the psychometric accuracy and the statistical reliability that was attained in these large-scale studies, the differences in interpretation cannot be attributed to chance. Differences in composition of the item pools must be responsible.
Saucier (2002a) interprets his first principal component as SD, for socially desirable qualities. On the one hand, this interpretation cannot be far off because the first principal component in any mixed set of positive and negative trait descriptors will be close to the desirability axis. On the other, it masks the fact that the first principal component bends toward whatever content is best represented in the item pool. For an extreme example, if that pool were overloaded with fairly neutral extraversion and introversion items, the first principal component would appear as extraverted desirability. Therefore, active steps have to be taken to justify the desirability interpretation.
I propose to define the p factor of personality as the individuals’Desirability. The most obvious operational definition of that variable consists of obtaining a score by weighting the items proportional to their desirability values. Both these values and the item scores are best expressed as positive and negative deviations from the neutral midpoint of the scale. In the absence of desirability values, the first principal component of a heterogeneous and representative set of traits will closely approximate the desirability variable. The desirability score reflects the extent to which an individual is assessed to have desirable versus undesirable qualities. The result will be that most people are found to be desirable, although some are more desirable than others. A few people would be assessed to be undesirable.
The implied conception of personality is literally perpendicular to the neutral view according to which, for example, there are no right or wrong answers to the items of a questionnaire, and by which all people are equally desirable, just different. One could of course use the desirability variable just to partial it out, and retain a value-free, neutrally descriptive account of personality, as in Saucier’s (1994) model. Here, on the contrary, it functions as the pivot around which the personality hypersphere revolves. The present approach is comparable to emphasizing the g factor of intelligence, rather than its multidimensional conception according to which people are just differently intelligent (even though no one, to my knowledge, has gone as far as to partial out g). There can hardly be any doubt that capitalizing on p provides the most realistic account of personality.
In the present context, the social part of social desirability is terminologically dubious. It could be used in opposition to personal desirability, but then the proper specification would be intersubjective versus subjective. In its actual use, SD refers primarily to impression management in self-report. This socially desirable responding (SDR) may be an interesting topic of study in its own right, but it is not at issue here. People have desirable and undesirable traits; they show overall differences in the extent to which that is the case; there is substantial agreement among third persons, and even between self and other, about someone’s desirability score; its heredity coefficient is undoubtedly in the same order of magnitude as with other traits, as it is a linear combination of them. Socially desirable responding is orthogonal to these individual differences: In a Persons Assessors Situations design with Desirability as the dependent variable, SDR is an Assessors main effect (e.g., a self-assessment may be relatively socially desirable), and/or a Situations effect (e.g., a personnel selection context gives rise to elevated scores), and/or some interaction effect, but not a Persons or individual differences effect. The p component concerns the latter.
Carrying out the slight rotation, if needed, to align the first principal component in any particular data set with the desirability variable should prove helpful in solving the vexing problem of indeterminate rotational positions of components. Saucier (2002a) has already documented that varimax rotation does not help in this respect: Across data sets, the positions of unrotated principal components were at least as replicable as were varimaxed components. Among the principal components, the first is by far the most replicable one. Across differently composed sets of variables, however, part of this stability gets lost (as discussed earlier). Anchoring p at the desirability values, which are external to the studies, should enhance replicability.
The p-oriented model produces another taxonomic lever, namely, a measure of the representativeness of a set of personality traits or items, in the shape of the correlation between the first principal component of the set and the desirability variable. In a set overloaded with fairly neutral extraversion-introversion items attracting the first principal component, that correlation would be clearly below unity. In a heterogeneous set of neutral items, the desirability variable would be unstable, again lowering the correlation. In the spirit of the lexical axiom, such sets would be judged insufficiently representative. The proposed measure simulates that judgment.
The Two-Dimensional Level
Upon extracting p, a residual remains in the shape of a matrix of part scores. The first principal component of that residual matrix comes close to the second principal component of the original scores, at least in a representative set of variables. Taking p as the ordinate, a 45-deg counterclockwise rotation of the two components including p will produce an X structure, or a flat version of the double cone. The upper and lower segments contain the most unambiguously positive and negative, or consonant, traits; the left and right segments contain the most relatively neutral and discordant traits. The abridged semicircumplex structure at this level contains two bipolar facet vectors running from 11 o’clock to 5 o’clock and from 1 to 7 in addition to the 12 to 6 p vector; the relatively neutral traits are left unaccounted for by the model, as their projections on the vectors will be very low.
Substantively, the plane would resemble, but not be identical to, the interpersonal circumplex (Wiggins, 1980), the I II or Agreeableness Extraversion slice of the 5-D structure, Digman’s (1997) plane, and the like. In a perfectly representative set of traits as defined earlier, the model plane would be identical to the plane formed by the first two (rotated) principal components; this property makes it a good candidate for a canonical or reference structure. Its suitability for that purpose is enhanced by the absence of rotational freedom at this level: The positions of the model vectors are indirectly prescribed by the desirability values of the traits. Theoretical criteria, as in the interpersonal circumplex, or the simple-structure criterion as in 5-D models, are insufficiently capable of serving that reference function.
In the rationale of the semicircumplex model, the transition from one p dimension to two dimensions means a spreading of the desirability component, in the manner of the unfolding of a fan. The primordial one becomes diluted in the process, like the g factor of intelligence does when it is spread over two or more dimensions. Following elementary rules of parsimony, the transition should not be made lightly; the burden of proof is on those who take the step. Psychometrics offers an adequate procedure for this proof: Moredimensional assessments of personality should be shown to have sufficient incremental validity over the p component. This requirement implies that an assessment of p, as a baseline variable, would have to be part of any empirical study of personality.
Incremental validity of variables other than p would necessarily imply that variance orthogonal to it, thus neutral variance, is valid. This implication bridges the present family of models and those that capitalize on neutral variance, like Peabody’s (1984) and Saucier’s (1994; Saucier et al., 2001). In fact, the latter model is the complement of the Semi-Circumplex, at the present and subsequent dimensional levels; it fills in what the present model leaves empty. Although the basic assumption—potential incremental validity of neutral variance—is thus necessarily the same, a strategic difference remains at the executive level. In the semicircumplex approach, neutral variance is assessed indirectly, by suppressing the p variance from consonant traits rather than directly, as in Saucier (1994). The reason was given earlier: Discordant personality concepts are difficult to handle.
Semicircumplex Spheres and Hyperspheres
The three-dimensional member of the model family arises as follows: Add the second principal component of the matrix of residual scores (after removing p); retain the vertical orientation so that a globe is formed with the positive traits on the northern hemisphere and the negative traits on the southern one; perform an orthogonal rotation of the three axes including p so that they become equidistant (the angles being 54.7 deg, with cosine ; further constraints are discussed later) from the vertical axis. All this is in correspondence with the double cone model. Now form three slices (circumplexes) by taking two rotated axes at a time. The projection of p on these tilted planes has the 12 o’clock to 6 o’clock direction, and the 3 o’clock and 9 o’clock positions are on the equator. Additional model vectors are constructed running from 11 to 5 and from 1 to 6, as in the two-dimensional member of the model family.
The central positions in this structure are taken by the 12 to 6 vectors—to be labeled I/II, I/III, and II/III—that are the bisectrices of the right angle between the two rotated principal components forming the circumplex. The I, II, and III axes themselves merely guard the boundaries of the model structure; as such, they have no place or name in the model. The central model vectors appear to be close to p, namely, at a distance of 35.3 deg (with cosine .816 or ; generally, √̅2̅/̅n, where n is the number of dimensions). Note that this oblique structure arises as a side effect of an orthogonal rotation, not through some more liberal oblique rotation procedure as such. The central model vectors are thus much more saturated with desirability than are the factors themselves; at all dimensional levels of the model, they share exactly as much variance with p as do the orthogonal factors.
What is new about this structure is that mixtures or blends of factors have stolen the central place that used to belong to the factors. Instead of being derivatives, the bisectrices of the factor pairs have become the central concepts. This play of musical chairs comes about because of the closer association of the central vectors with p, which entitles them to their position. In passing, the model resolves the uneasiness of inserting orthogonal axes into an essentially oblique structure; it rigorously defines oblique axes without giving up the convenience of an orthogonal base. The only price is that the number of musical chairs has to be increased, from four dimensions onward: There are n(n − 1)/2 central vectors, with n the number of dimensions or factors. However, that extension will be welcomed by those who have always wondered whether five is all there is. The model has shaken off the last remnants of simple-structure thinking. Parenthetically, I note that the model is equally appropriate in other domains, notably, intelligence.
With four dimensions, the rotated factors are at an angle of 60 deg with respect to the p factor; the central model vectors are at 45 deg from that pivot. With five dimensions, the factors are at 63.4 deg, and the central vectors are at 50.7 deg. Still, the model rotation maximizes the sum of the correlations of the central axes with p, and in that sense minimizes their average neutralness. Conversely, any other orthogonal rotation of these dimensions (e.g., varimax) is inferior in this respect: It takes in more neutral traits, which are less representative of the domain.
With three or more dimensions, the model leaves freedom of spin. A three-dimensional structure, for example, may be rotated around its vertical p-axis without violating the model. For reasons of continuity, this freedom may be used for maximizing the correspondence of the rotated factors with the current varimax factors, particularly, the 5-D model factors. This amounts to some lowering of the positive poles of the current dimensions I and III toward the hyperequator, and some lifting of the others. One may speculate, for example, that the American lexical extraversion factor loses its aggressive connotation and moves in the direction of sociability. However, it is difficult to gauge what the substantive effects of the joint rotation will be on all the versions in all the different languages (see, e.g., Saucier et al., 2000) that have been proposed. The labels of the 5-D model are probably used in a manner vague enough to permit this twisting. (Agreeableness and conscientiousness, in particular, do not even fit their present axes; see Hofstee et al., 1992.)
From the three-dimensional level on, there is some redundancy between model vectors at different levels. At the top level, there is the one vector. At the second level, two additional bipolar vectors appear, which satisfy the requirement of being 30 deg removed from p. At the third, we find three semicircumplexes with three model vectors each; at the fourth, there are 6 3 at the fifth, the AB5SC model with 30 vectors appears; in general, at the nth level from 3 on, there are 1.5n(n − 1) vectors specific to that level. In successively adding levels, the cumulative number of model vectors thus becomes 1, 3, 12, 30, and 60. From the third level on, it appears impossible to rotate the central vectors in such a way that all the additional vectors stay at least 30 deg away from the ones at the second level. Thus some vectors would have indistinguishable interpretations.
One strategy would be to settle for a particular dimensionality of the trait space. That would prevent overlap and would simplify things in general. The foremost drawback is that from three dimensions onward the most central trait concepts would be missed. Furthermore, that strategy would only stir up the debate on the dimensionality of the trait space, to which there is no cogent solution; it would thus frustrate the attainment of a canonical structure rather than contribute to it. The other, preferable, strategy is to adopt the model family as a whole, including as many (or as few) levels as will appear to be needed, and deleting concepts at lower levels that are virtual clones of those at higher levels. The foreseeable result of this strategy is maximal convergence of structures at each level, and maximal efficiency in communicating about personality up to a particular level. In this manner, the family model may become a model family.
Conclusion
This probe into the credentials and future of the 5-D approach to personality ends in cautious optimism. Because of its reliance on the questionnaire method, the 5-D paradigm stays at the phenotypic level; however, an efficient and coherent description of personality is indispensable also for research on genotypic and other determinants of individual differences. The exploitation of the lexical axiom, with its rich history dating back into the nineteenth century, in combination with PCA of large data sets that became feasible only in the last decades of the twentieth century, has provided a firm base for efficiently and coherently describing personality differences. Of the several and diverging taxonomic models that have arisen in the 5-D tradition, I used elements to design the contours of an integrative structure that may serve scientific and applied communication.
In the process, the penetrating evaluative aspect of personality description exerted its influence. Its pervasiveness constitutes a fundamental and often frustrating problem to the field. I have chosen to adopt the strategy recommended to bridge players who find themselves in a squeeze: Relax and enjoy it. Desirability cannot be circumvented or suppressed without sacrificing the first principal component of personality description. So it might as well be squarely faced and put in the most central position. Giving in to the desirability component of personality will in all likelihood be rewarded with a more coherent, stable, and internationally replicable conception of personality structure.
Bibliography:
- Almagor, M., Tellegen, A., & Waller, N. G. (1995). The Big Seven model: Across-cultural replication and further exploration of the basic dimensions of natural language trait descriptors. Journal of Personality and Social Psychology, 69, 300–307.
- Asendorpf, J. B., & Van Aken, M. A. G. (1999). Resilient, overcontrolled and undercontrolled personality prototypes in childhood: Replicability, predictive power, and the trait/type issue. Journal of Personality and Social Psychology, 77, 815–832.
- Block,J.(1995).Acontrarian viewof thefive-factor approach topersonality description. Psychological Bulletin, 117, 187–215.
- Bouchard, T. J., Jr. (1993). Genetic and environmental influences on adult personality: Evaluating the evidence. In J. Hettema & I. J.
- Deary (Eds.), Foundations of personality (pp. 15–44). Deventer, Netherlands: Kluwer.
- Brand, C. (1994). Open to experience–closed to intelligence: Why the ‘big five’are really the comprehensive six. European Journal of Personality, 8, 299–310.
- Brokken, F. B. (1978). The language of personality. Meppel, Netherlands: Krips.
- Brunner, H. G., Nelen, M., Breakfield, X. O., Roppers, H. H., & Van Oost, B. A. (1993). Abnormal behavior associated with a point mutation in the structural gene for monoamine oxidase A. Science, 262, 50–55.
- Buss, D. M. (1996). Social adaptation and five major factors of personality. In J. S. Wiggins (Ed.), The five-factor model of personality: Theoretical perspectives (pp. 180–207). New York: Guilford.
- Carlson, R. (1971). Where is the person in personality research? Psychological Bulletin, 75, 203–219.
- Costa, P. T., Jr., & McCrae, R. R. (1992). Revised NEO Personality Inventory (NEO PI-R) and NEO Five-Factor Inventory (NEOFFI) professional manual. Odessa, FL: Psychological Assessment Resources.
- Cruse, D. B. (1965). Social desirability scale values of personal concepts. Journal of Applied Psychology, 49, 342–344.
- De Boeck, P. (1978). On the evaluative factor in the trait scales of Peabody’s study of trait inferences. Journal of Personality and Social Psychology, 36, 619–621.
- De Raad, B. (1992). The replicability of the Big Five personality dimensions in three word-classes of the Dutch language. European Journal of Personality, 6, 15–29.
- De Raad, B. (2000). The big five personality factors: The psycholexical approach to personality. Goettingen, Germany: Hogrefe & Huber.
- De Raad, B., Perugini, M., & Szirmák, Z. (1997). In pursuit of a cross-lingual reference structure of personality traits: Comparisons among five languages. European Journal of Personality, 11, 167–185.
- Digman, J. M. (1990). Personality structure: Emergence of the fivefactor model. In M. R. Rosenzweig & L. W. Porter (Eds.), Annual review of psychology (Vol. 41, pp. 417–446). Palo Alto, CA: Annual Reviews.
- Digman, J. M. (1997). Higher-order factors of the big five. Journal of Personality and Social Psychology, 73, 1246–1256.
- Digman, J. M., & Inouye, J. (1986). Further specification of the five robust factors of personality. Journal of Personality and Social Psychology, 50, 116–123.
- Eysenck, H. J. (1992). Dimensions of personality: 16, 5, 3? Criteria for a taxonomic paradigm. Personality and Individual Differences, 13, 667–673.
- Eysenck, H. J., & Rachman, S. (1965). The causes and cures of neurosis. London: Routledge.
- Galton, F. (1884). Measurement of character. Fortnightly Review, 36, 179–185.
- Goff, M., & Ackerman, P. L. (1992). Personality-intelligence relations: Assessment of typical intellectual engagement. Journal of Educational Psychology, 84, 537–552.
- Goldberg, L. R. (1982). From Ace to Zombie: Some explorations in the language of personality. In C. D. Spielberger & J. N. Butcher (Eds.), Advances in personality assessment, (Vol. 1, pp. 203– 234). Hillsdale, NJ: Erlbaum.
- Goldberg, L. R. (1992a). The development of markers for the BigFive factor structure. Psychological Assessment, 4, 26–42.
- Goldberg, L. R. (1992b, June). The structure of phenotypic personality traits (or the magical number five, plus or minus zero). Keynote lecture presented at the 6th European Conference on Personality, Groningen, Netherlands.
- Goldberg, L. R. (1993a). The structure of personality traits: Vertical and horizontal aspects. In D. C. Funder, R. D. Parke, C. Tomlinson-Keasy, & K. Widaman (Eds.), Studying lives through time: Personality and development (pp. 169–188). Washington, DC: American Psychological Association.
- Goldberg, L. R. (1993b). The structure of phenotypic personality traits. American Psychologist, 48, 26–43.
- Gower, J. C. (1971). A general coefficient of similarity and some of its properties. Biometrics, 27, 857–871.
- Haven, S., & Ten Berge, J. M. F. (1977). Tucker’s coefficient of congruence as a measure of factorial invariance:An empirical study. (Heymans Bulletin, No. 290 EX). University of Groningen, Netherlands.
- Hendriks, A. A. J. (1997). The construction of the Five-Factor Personality Inventory. Unpublished doctoral dissertation, University of Groningen, Netherlands.
- Hendriks, A. A. J., Hofstee, W. K. B., & De Raad, B. (1999). The Five-Factor Personality Inventory (FFPI). Personality and Individual Differences, 27, 307–325.
- Herbst, J. H., Zonderman, A. B., McCrae, R. R., & Costa, P. T., Jr. (2000). Do the dimensions of the Temperament and Character Inventory map a simple genetic architecture? Evidence from molecular genetics and factor analysis. American Journal of Psychiatry, 157, 1285–1290.
- Heymans, G. (1929). Inleiding in de speciale psychologie [Introduction to special psychology]. Haarlem, Netherlands: Bohn.
- Hofstee, W. K. B. (1990). The use of everyday personality language for scientific purposes. European Journal of Personality, 4, 77–88.
- Hofstee, W. K. B. (1994a). Who should own the definition of personality? European Journal of Personality, 8, 149–162.
- Hofstee, W. K. B. (1994b). Are we looking for parsimony, or what? European Journal of Personality, 8, 335–339.
- Hofstee, W. K. B. (1994c). Personality and factor analysis: Bind or bond? Zeitschrift für Differentielle und Diagnostische Psychologie, 15, 173–183.
- Hofstee, W. K. B. (1999). Big-Five-profielen van persoonlijkheidsstoornissen [Big-Five profiles of personality disorders]. De Psycholoog, 34, 381–384.
- Hofstee, W. K. B. (2001). Personality and intelligence: Do they mix? In J. Collis & S. Messick (Eds.), Intelligence and personality: Bridging the gap in theory and measurement. Mahwah, NJ: Erlbaum.
- Hofstee, W. K. B., & Arends, L. R. (1994). The heuristic potential of the abridged big-five dimensional circumplex (AB5C) model: Explaining the chiasmic illusion. Psychologica Belgica, 34, 195–206.
- Hofstee, W. K. B., De Raad, B., & Goldberg, L. R. (1992). Integration of the Big Five and circumplex approaches to trait structure. Journal of Personality and Social Psychology, 63, 146–163.
- Hofstee, W. K. B., & Hendriks, A. A. J. (1998). The use of scores anchored at the scale midpoint in reporting people’s traits. European Journal of Personality, 12, 219–228.
- Hofstee, W. K. B., Kiers, H. A. L., De Raad, B., Goldberg, L. R., & Ostendorf, F. (1997). A comparison of Big-Five structures of personality traits in Dutch, English, and German. European Journal of Personality, 11, 15–31.
- Hofstee, W. K. B., Ten Berge, J. M. F., & Hendriks, A. A. J. (1998). How to score questionnaires. Personality and Individual Differences, 25, 897–909.
- Horst, P. (1965). Factor analysis of data matrices. New York: Holt, Rinehart & Winston.
- Jang, K. L., McCrae, R. R., Angleitner, A., Riemann, R., & Livesley, J. (1998). Heritability of facet-level traits in a cross-cultural twin sample: Support for a hierarchical model of personality. Journal of Personality and Social Psychology, 74, 1556–1565.
- John, O. P. (1990). The ‘Big Five’ factor taxonomy: Dimensions of personality in the natural language and in questionnaires. In L. A. Pervin (Ed.), Handbook of personality: Theory and research (pp. 66–100). New York: Guilford.
- Krueger, R. F. (2000). Phenotypic, genetic, and non-shared environmental parallels in the structure of personality: A view from the Multidimensional Personality Questionnaire. Journal of Personality and Social Psychology, 79, 1057–1067.
- Loehlin, J. C. (1992). Genes and environment in personality development. Newbury Park, CA: Sage.
- Magnusson, D. (1992). Back to the phenomena: Theory, methods, and statistics in psychological research. European Journal of Personality, 6, 1–14.
- McAdams, D. P. (1992). The five-factor model in personality: Acritical appraisal. Journal of Personality, 60, 329–361.
- McCrae, R. R. (1990). Traits and trait names: How well is openness represented in natural languages? European Journal of Personality, 4, 119–129.
- McCrae, R. R. (1994). Openness to experience: Expanding the boundaries of Factor V. European Journal of Personality, 8, 251–272.
- McCrae, R. R., & Costa, P. T., Jr. (1987).Validation of the five-factor model of personality across instruments and observers. Journal of Personality and Social Psychology, 52, 81–90.
- McCrae, R. R., & Costa, P. T., Jr. (1992). Discriminant validity of NEO-PIR facet scales. Educational and Psychological Measurement, 52, 229–237.
- Millon, T. (1990). The disorders of personality. In L. A. Pervin (Ed.), Handbook of personality: Theory and research (pp. 339– 370). New York: Guilford.
- Ostendorf, F. (1990). Sprache und Persönlichkeitsstruktur: Zur Va-lidität des Fünf-Faktoren-Modells der Persönlichkeit [Language and personality structure: On the validity of the fivefactor model of personality]. Regensburg, Germany: S. Roderer Verlag.
- Pawlik, K. (1968). Dimensionen des Verhaltens [Dimensions of behavior]. Bern, Switzerland: Huber.
- Peabody, D. (1967). Trait inferences: Evaluative and descriptive aspects. Journal of Personality and Social Psychology Monograph, 7 (4, Whole No. 644).
- Peabody, D. (1984). Personality dimensions through trait inferences. Journal of Personality and Social Psychology, 46, 384–403.
- Peabody, D., & Goldberg, L. R. (1989). Some determinants of factor structures from personality-trait descriptors. Journal of Personality and Social Psychology, 57, 552–567.
- Plomin, R., & Caspi, A. (1998). DNA and personality. European Journal of Personality, 12, 387–407.
- Riemann, R. (1997). Persönlichkeit: Fähigkeiten oder Eigenschaften? [Personality: Capabilities or traits?]. Lengerich, Germany: Pabst Science.
- Robins, R. W., John, O. P., Caspi, A., Moffit, T. E., & StouthamerLoeber, M. (1996). Resilient, overcontrolled, and undercontrolled boys: Three replicable personality types. Journal of Personality and Social Psychology, 70, 157–171.
- Saucier, G. (1992). Benchmarks: Integrating affective and interpersonal circles with the Big-Five personality factors. Journal of Personality and Social Psychology, 62, 1025–1035.
- Saucier, G. (1994). Separating description and evaluation in the structure of personality attributes. Journal of Personality and Social Psychology, 66, 141–154.
- Saucier, G. (2002a). What is more replicable than the Big Five? Broader-factor structures from English lexical descriptors. Manuscript submitted for publication.
- Saucier, G. (2002b). Orthogonal markers for orthogonal factors: The case of the Big Five. Journal of Research in Personality, 36, 1–31.
- Saucier, G., Hampson, S. E., & Goldberg, L. R. (2000). Crosslanguage studies of lexical personality factors. In S. E. Hampson (Ed.), Advances in personality psychology (Vol. 1, pp. 1–36). London: Routledge.
- Saucier, G., Ostendorf, F., & Peabody, D. (2001). The nonevaluative circumplex of personality adjectives. Journal of Personality, 69, 537–582.
- Tellegen, A. (1982). Brief manual for the Multidimensional Personality Questionnaire. Unpublished manuscript, University of Minnesota, Minneapolis.
- Tellegen, A. (1993). Folk concepts and psychological concepts of personality and personality disorder. Psychological Inquiry, 4, 122–130.
- Ten Berge, J. M. F. (1999). A legitimate case of component analysis of ipsative measures and partialling the mean as an alternative to ipsatization. Multivariate Behavioral Research, 34, 89–102.
- Ten Berge, J. M. F., & Hofstee, W. K. B. (1999). Coefficients and reliabilities of unrotated and rotated components. Psychometrika, 64, 83–90.
- Tupes, E. C., & Christal, R. E. (1956/1992). Recurrent personality factors based on trait ratings. Technical Report No. ASD-TR-6197, US Air force, Lackland Air Force Base, TX; Journal of Personality, 60, 225–251.
- Wiggins, J. S. (1980). Circumplex models of interpersonal behavior. In L. Wheeler (Ed.), Review of personality and social psychology (Vol. 1, pp. 265–294). Beverly Hills, CA: Sage.
- Zegers, F. E., & Ten Berge, J. M. F. (1985). A family of association coefficients for metric scales. Psychometrika, 50, 17–24.




