Cognitive Psychology Of Explanation-Based Learning Research Paper

1. Introduction

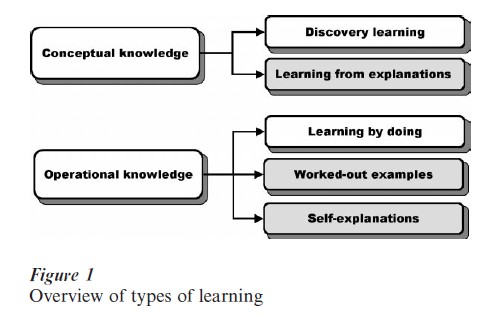
In learning, a distinction can be made between acquiring conceptual (declarative) knowledge (principles, systems, and processes from a domain) and operational (procedural) knowledge (domain-specific tasks, such as solving problems). Both types of knowledge can be acquired in learning that has a more discovery or experiential character or by explanation based learning (see e.g., Glaser 1966, Zhu and Simon 1987).

In discovery or experiential learning, theory or skills are not introduced directly by the teacher or the learning material but have to be induced from the environment by learners themselves. For conceptual knowledge, this can take for example the form of scientific discovery learning with simulations (e.g., de Jong and van Joolingen 1998). For operational knowledge, experiential learning is embodied in ‘learning by doing.’ After having acquired the basic conceptual knowledge, learners start to solve problems by themselves (see e.g., Anderson et al. 1981).

Explanation-based learning comes very close to our traditional, classroom-related idea of teaching and learning and involves a teacher (or a learning material) who explains or shows the learner what to know or how to act. For conceptual knowledge, explanations lay out the basic elements and relations between these elements (concepts and relations) from the domain and may contain descriptions of new concepts in terms of known principles, validation of new concepts by logical derivations, presentation of examples and nonexamples, explicitation of causality, etc. These explanations take the form of text or visuals of many kinds (e.g., graphs, diagrams, animations). For operational knowledge, ‘explanations’ can take the form of step-by-step instantiated procedures. For problem solving these are called worked-out examples. These worked-out examples can be extended by ‘annotations’ that further explain to learners the related theoretical principles or generalizable problem-solving procedures and strategies. Learners can be provided with these annotations by the teacher or the learning material, but they can also generate explanations themselves, in which case they are called ‘self-explanations.’

Figure 1 summarizes the different types of learning. The explanation-based types of learning are indicated in gray in the figure. ‘Learning from explanations’ refers to learning conceptual knowledge from a teacher or from instructional material. The literature on learning (processes) in this area can be found in studies on studying text, hypertext, and other types of ‘expository’ (multimedia) learning material. In this research paper, there is an emphasis on learning operational knowledge from worked-out examples and from self-explanations.

2. Learning From Worked-Out Examples

Traditionally, textbooks (on e.g., physics) are built up in such a way that first theory (conceptual knowledge) is explained, then example problems are presented, and subsequently students have to solve problems themselves. Anderson et al. (1981) studied students solving geometry proof problems and found that students made heavy use of examples. In solving a novel problem, they try to find similarities and relate characteristics of the new problem to the characteristics of the old one. Pirolli and Anderson (1985) studied students learning recursion in programming. They report that, in an initial stage, 18 of 19 students writing programs containing recursion used a previous example, and students spent 34.3 percent of their time examining this example. In this ‘learning by analogy,’ students first modify the solutions of examples given and then create ‘new problem-solving operators which can apply to future problems’ (p. 242). Pirolli and Anderson (1985) further point out that students only rely on analogical problem solving in novel or difficult situations, such as when learners encounter an ‘impasse’ in the problem-solving process. When they are more experienced they have built a knowledge base that contains ‘compiled knowledge,’ which is knowledge that is dedicated to solving specific kind of problems and that may lead to fast and errorless problem solving.

A theory that supports the idea that worked-out examples should be used in initial stages of learning is ‘cognitive load theory’ (Sweller and Cooper 1985). This theory takes as a starting point that proficient problem solving requires schemas and rules. Schemas are cognitive constructs that help to recognize problem types and trigger the adequate rules from memory. Learning to solve problems therefore involves the processes of ‘schema acquisition’ and ‘rule automation’ (Ward and Sweller 1990). If learners, in an initial stage, have not yet acquired schemas they have to rely on general (weak) problem-solving procedures such as ‘means–ends analysis’ to find rules. Means– ends analysis is a general problem-solving procedure in which comparisons between the current problem state and the goal state (solution) guide the search for operators that help to bring the current state to the goal state. These weak problem-solving procedures require large cognitive resources because problem solvers have to ‘simultaneously consider and make decisions about the current problem state, the goal state, differences between states, and problem solving operators that can be used to reduce such differences’ (Ward and Sweller 1990, p. 3). With worked-out problems learners can concentrate on problem states and their associated moves, thus reducing cognitive load and preventing potential cognitive ‘overload.’ In several studies, Sweller and associates found beneficial effects of learning with worked-out examples compared to open problems.

3. Learning From Self-Explanations

Anderson et al. (1981) pointed to the fact that learning from worked-out problems and using analogies in solving new problems only works on short-term notice because students do not remember examples that well and that the matching of the two problems is very ‘syntactic’ and thus superficial in nature. In a similar vein, Zhu and Simon (1987) found that students solving quadratic algebraic expressions (e.g., x ax b) sometimes matched a new problem on one condition with the example (e.g., that the sum of the numerical factor should equal the coefficient of the linear term of the quadratic) but then failed to look at another necessary condition (e.g., that the product of the factors should equal the constant term) (see Zhu and Simon 1987, p. 145). These findings suggest that analogy-based problem solving may easily lead to using inadequate problem-solving procedures. The learning process in using worked-out examples may thus have a more reproductive character, leading to more superficial knowledge without the necessary abstractions needed for transfer. A solution can be found by providing students with annotated examples in which annotations link the examples to theoretical principles and transferable problem-solving knowledge. These explanations of the problem-solving process can also be generated by students themselves (‘self-explanations’). According to Chi and van-Lehn (1991) ‘A self-explanation is a comment about an example statement that contains domain relevant information over and above what was stated in the example line itself’ (p. 69). Theories of ‘self-explanation’ try to combine the best of both worlds. Together with providing basic information or partexplanations, students are required to reformulate information themselves. This stimulates the integration of the new information and prior knowledge and excites generalization. At the same time, too high a cognitive load is avoided.

Of the studies listed by Chi and vanLehn (1991), several found that students learn successfully from examples while other studies indicate that learning from examples does not lead to the ability to solve new problems. Chi and vanLehn (1991) reason that in the successful studies students applied self-explanations. Several studies indeed found this relation between success and self-explanations. Chi et al. (1989) and Ferguson-Hessler and de Jong (1990) found that good problem solvers generate more self-explanations while studying a text and example problems than poor problem solvers. Ferguson-Hessler and de Jong (1990) found that good problem solvers tended to explain principles and problem-solving steps to themselves, whereas poor problem solvers took the information for granted.

It is, however, not only the amount of self-explanations but also the quality of them that matters. Chi and van-Lehn (1991) state that there are two ways to generate self-explanations. One is a more deductive way in which connections are made with theoretical concepts and principles (e.g., from the text). Bielaczyc et al. (1995) mention that in self-explanations students link features of the examples to concepts that were introduced in the preceding text. The second type of self-explanation that Chi and van-Lehn identified follows an inductive route and concerns making abstractions or generalizations from a specific example given. Chi and van-Lehn (1991) found, for example, that self-explanations generated by students while studying worked-out physics problems mainly concerned justifying the action in the problem’s solution, by extending the conditions of the action and following up the consequences of the action.

Similarly, Bielaczyc et al. (1995) mention identifying the processes and rationale underlying actions in the example (LISP-programming) problem as a self-explanation strategy. This may explain differences found in the use of examples by good and poor problem solvers in the Chi et al. (1989) study. They found that good problem solvers used the examples as prompts or references (so using abstractions) whereas the poor problem solvers used them as analogies in solving new problems (which indicates more superficial comparisons). In addition to these two types of self-explanations, students also use explanations to ‘plan, monitor, and evaluate their comprehension and strategy use’ (Bielaczyc et al. 1995, p. 249). Also, for this type of self-explanation Ferguson-Hessler and de Jong (1990) found differences between good and poor problem solvers. Good problem solvers had metaknowledge and were able to assess when they understood something; poor problem solvers, to the contrary, generally overestimated their understanding of the domain.

4. Instructional Consequences

Studies cited above have shown advantages to learning with worked-out problems but also clearly suggest that favorable effects will only be reached when students process these worked-out examples in a ‘deep’ way by generating self-explanations. A way to foster this is to train or stimulate students to generate self-explanations. Bielaczyc et al. (1995) found that students who received an explicit training in generating self-explanations indeed improved on this and gained higher performance than a control group that did not receive this instruction. The training that Bielaczyc et al. gave was very domain-specific, but Chi et al. (1994) also found beneficial results from providing students with quite general hints to generate explanations for themselves.

Bibliography:

1. Anderson J R, Greeno J G, Kline P J, Neeves D M 1981 Acquisition of problem-solving skills. In: Anderson J R (ed.) Cognitive Skills and their Acquisition: Carnegie Symposium on Cognition (16th: 1980: Carnegie-Melton University. Erlbaum, Hillsdale, NJ, pp. 191–230
2. Bielaczyc K, Pirolli P L, Brown A L 1995 Training in self-explanation and self-regulation strategies: Investigating the effects of knowledge acquisition activities on problem solving. Cognition and Instruction 13: 221–52
3. Chi M T H, Bassok M, Lewis M W, Reimann P, Glaser R 1989 Self-explanations: How students study and use examples in learning to solve problems. Cognitive Science 13: 145–82
4. Chi M T H, van Lehn K A 1991 The content of physics self-explanations. The Journal of the Learning Sciences 1: 69–105
5. Chi M T H, de Leeuw N, Chiu M-H, Lavancher C 1994 Eliciting self-explanations improves understanding. Cognitive Science 18: 439–77
6. de Jong T, van Joolingen W R 1998 Scientific discovery learning with computer simulations of conceptual domains. Review of Educational Research 68: 179–202
7. Ferguson-Hessler M G M, de Jong T 1990 Studying physics text; differences in study processes between good and poor performers. Cognition and Instruction 7: 41–54
8. Glaser R 1966 Variables in discovery learning. In: Shulma L S, Keislar E R (eds.) Learning by Discovery. A Critical Appraisal. Rand McNally, Chicago, pp. 13–26
9. Pirolli P L, Anderson J R 1985 The role of learning from examples in the acquisition of recursive programming skills. Canadian Journal of Psychology 39: 240–72
10. Sweller J, Cooper G A 1985 The use of worked examples as a substitute for problem solving in learning algebra. Cognition and Instruction 2: 59–89
11. Ward M, Sweller J 1990 Structuring effective worked examples. Cognition and Instruction 7: 1–39
12. Zhu X, Simon H A 1987 Learning mathematics from examples and by doing. Cognition and Instruction 4: 137–66