View sample psychometric characteristics of assessment procedures research paper. Browse other research paper examples and check the list of psychology research paper topics for more inspiration. If you need a psychology research paper written according to all the academic standards, you can always turn to our experienced writers for help. This is how your paper can get an A! Feel free to contact our custom writing service for professional assistance. We offer high-quality assignments for reasonable rates.
“Whenever you can, count!” advised Sir Francis Galton (as cited in Newman, 1956, p. 1169), the father of contemporary psychometrics. Galton is credited with originating the concepts of regression, the regression line, and regression to the mean, as well as developing the mathematical formula (with Karl Pearson) for the correlation coefficient. He was a pioneer in efforts to measure physical, psychophysical, and mental traits, offering the first opportunity for the public to take tests of various sensory abilities and mental capacities in his London Anthropometric Laboratory. Galton quantified everything from fingerprint characteristics to variations in weather conditions to the number of brush strokes in two portraits for which he sat. At scientific meetings, he was known to count the number of times per minute members of the audience fidgeted, computing an average and deducing that the frequency of fidgeting was inversely associated with level of audience interest in the presentation.
Academic Writing, Editing, Proofreading, And Problem Solving Services
Get 10% OFF with 24START discount code
Of course, the challenge in contemporary assessment is to know what to measure, how to measure it, and whether the measurements are meaningful. In a definition that still remains appropriate, Galton defined psychometry as the “art of imposing measurement and number upon operations of the mind” (Galton, 1879, p. 149). Derived from the Greek psyche (ψνχή, meaning soul) and metro ( μετρώ , meaning measure), psychometry may best be considered an evolving set of scientific rules for the development and application of psychological tests. Construction of psychological tests is guided by psychometric theories in the midst of a paradigm shift. Classical test theory, epitomized by Gulliksen’s (1950) Theory of Mental Tests, has dominated psychological test development through the latter two thirds of the twentieth century. Item response theory, beginning with the work of Rasch (1960) and Lord and Novick’s (1968) Statistical Theories of Mental Test Scores, is growing in influence and use, and it has recently culminated in the “new rules of measurement” (Embretson, 1995).
In this research paper, the most salient psychometric characteristics of psychological tests are described, incorporating elements from both classical test theory and item response theory. Guidelines are provided for the evaluation of test technical adequacy.The guidelines may be applied to a wide array of psychological tests, including those in the domains of academic achievement, adaptive behavior, cognitive-intellectual abilities, neuropsychological functions, personality and psychopathology, and personnel selection. The guidelines are based in part upon conceptual extensions of the Standards for Educational and Psychological Testing (American Educational Research Association, 1999) and recommendations by such authorities as Anastasi and Urbina (1997), Bracken (1987), Cattell (1986), Nunnally and Bernstein (1994), and Salvia and Ysseldyke (2001).
Psychometric Theories
The psychometric characteristics of mental tests are generally derived from one or both of the two leading theoretical approaches to test construction: classical test theory and item response theory. Although it is common for scholars to contrast these two approaches (e.g., Embretson & Hershberger, 1999), most contemporary test developers use elements from both approaches in a complementary manner (Nunnally & Bernstein, 1994).
Classical Test Theory
Classical test theory traces its origins to the procedures pioneered by Galton, Pearson, Spearman, and E. L. Thorndike, and it is usually defined by Gulliksen’s (1950) classic book. Classical test theory has shaped contemporary investigations of test score reliability, validity, and fairness, as well as the widespread use of statistical techniques such as factor analysis.
At its heart, classical test theory is based upon the assumption that an obtained test score reflects both true score and error score. Test scores may be expressed in the familiar equation
Observed Score = True Score + Error
In this framework, the observed score is the test score that was actually obtained.The true scoreis thehypotheticalamount of the designated trait specific to the examinee, a quantity that would be expected if the entire universe of relevant content were assessed or if the examinee were tested an infinite number of times without any confounding effects of such things as practice or fatigue. Measurement error is defined as the difference between true score and observed score. Error is uncorrelated with the true score and with other variables, and it is distributed normally and uniformly about the true score. Because its influence is random, the average measurement error across many testing occasions is expected to be zero.
Many of the key elements from contemporary psychometrics may be derived from this core assumption. For example, internal consistency reliability is a psychometric function of random measurement error, equal to the ratio of the true score variance to the observed score variance. By comparison, validity depends on the extent of nonrandom measurement error. Systematic sources of measurement error negatively influence validity, because error prevents measures from validly representing what they purport to assess. Issues of test fairness and bias are sometimes considered to constitute a special case of validity in which systematic sources of error across racial and ethnic groups constitute threats to validity generalization.As an extension of classical test theory, generalizability theory (Cronbach, Gleser, Nanda, & Rajaratnam, 1972; Cronbach, Rajaratnam, & Gleser, 1963; Gleser, Cronbach, & Rajaratnam, 1965) includes a family of statistical procedures that permits the estimation and partitioning of multiple sources of error in measurement. Generalizability theory posits that a response score is defined by the specific conditions under which it is produced, such as scorers, methods, settings, and times (Cone, 1978); generalizability coefficients estimate the degree to which response scores can be generalized across different levels of the same condition.
Classical test theory places more emphasis on test score properties than on item parameters. According to Gulliksen (1950), the essential item statistics are the proportion of persons answering each item correctly (item difficulties, or p values), the point-biserial correlation between item and total score multiplied by the item standard deviation (reliability index), and the point-biserial correlation between item and criterion score multiplied by the item standard deviation (validity index).
Hambleton, Swaminathan, and Rogers (1991) have identified four chief limitations of classical test theory: (a) It has limited utility for constructing tests for dissimilar examinee populations (sample dependence); (b) it is not amenable for making comparisons of examinee performance on different tests purporting to measure the trait of interest (test dependence); (c) it operates under the assumption that equal measurement error exists for all examinees; and (d) it provides no basis for predicting the likelihood of a given response of an examinee to a given test item, based upon responses to other items. In general, with classical test theory it is difficult to separate examinee characteristics from test characteristics. Item response theory addresses many of these limitations.
Item Response Theory
Item response theory (IRT) may be traced to two separate lines of development. Its origins may be traced to the work of Danish mathematician Georg Rasch (1960), who developed a family of IRT models that separated person and item parameters. Rasch influenced the thinking of leading European and American psychometricians such as Gerhard Fischer and Benjamin Wright. A second line of development stemmed from research at the Educational Testing Service that culminated in Frederick Lord and Melvin Novick’s (1968) classic textbook, including four chapters on IRT written by Allan Birnbaum. This book provided a unified statistical treatment of test theory and moved beyond Gulliksen’s earlier classical test theory work.
IRT addresses the issue of how individual test items and observations map in a linear manner onto a targeted construct (termed latent trait, with the amount of the trait denoted by ). The frequency distribution of a total score, factor score, or other trait estimates is calculated on a standardized scale with a mean of 0 and a standard deviation of 1. An item characteristic curve (ICC) can then be created by plotting the proportion of people who have a score at each level of , so that the probability of a person’s passing an item depends solely on the ability of that person and the difficulty of the item. This item curve yields several parameters, including item difficulty and item discrimination. Item difficulty is the location on the latent trait continuum corresponding to chance responding. Item discrimination is the rate or slope at which the probability of success changes with trait level (i.e., the ability of the item to differentiate those with more of the trait from those with less). A third parameter denotes the probability of guessing. IRT based on the one-parameter model (i.e., item difficulty) assumes equal discrimination for all items and negligible probability of guessing and is generally referred to as the Rasch model. Two-parameter models (those that estimate both item difficulty and discrimination) and three-parameter models (those that estimate item difficulty, discrimination, and probability of guessing) may also be used.
IRT posits several assumptions: (a) unidimensionality and stability of the latent trait, which is usually estimated from an aggregation of individual item; (b) local independence of items,meaningthattheonlyinfluenceonitemresponsesisthe latent trait and not the other items; and (c) item parameter invariance, which means that item properties are a function of the item itself rather than the sample, test form, or interaction between item and respondent. Knowles and Condon (2000) argue that these assumptions may not always be made safely. Despite this limitation, IRT offers technology that makes test development more efficient than classical test theory.
Sampling and Norming
Under ideal circumstances, individual test results would be referenced to the performance of the entire collection of individuals (target population) for whom the test is intended. However, it is rarely feasible to measure performance of every member in a population. Accordingly, tests are developed through sampling procedures, which are designed to estimate the score distribution and characteristics of a target population by measuring test performance within a subset of individuals selected from that population. Test results may then be interpreted with reference to sample characteristics, which are presumed to accurately estimate population parameters. Most psychological tests are norm referenced or criterion referenced. Norm-referenced test scores provide information about an examinee’s standing relative to the distribution of test scores found in an appropriate peer comparison group. Criterion-referenced tests yield scores that are interpreted relative to predetermined standards of performance, such as proficiency at a specific skill or activity of daily life.
Appropriate Samples for Test Applications
When a test is intended to yield information about examinees’ standing relative to their peers, the chief objective of sampling should be to provide a reference group that is representative of the population for whom the test was intended. Sample selection involves specifying appropriate stratification variables for inclusion in the sampling plan. Kalton (1983) notes that two conditions need to be fulfilled for stratification: (a) The population proportions in the strata need to be known, and (b) it has to be possible to draw independent samples from each stratum. Population proportions for nationally normed tests are usually drawn from Census Bureau reports and updates.
The stratification variables need to be those that account for substantial variation in test performance; variables unrelated to the construct being assessed need not be included in the sampling plan. Variables frequently used for sample stratification include the following:
- Race (White, African American, Asian/Pacific Islander, Native American, Other).
- Ethnicity (Hispanic origin, non-Hispanic origin).
- Geographic Region (Midwest, Northeast, South, West).
- Community Setting (Urban/Suburban, Rural).
- Classroom Placement (Full-Time Regular Classroom, Full-Time Self-Contained Classroom, Part-Time Special Education Resource, Other).
- SpecialEducationServices(LearningDisability,Speechand Language Impairments, Serious Emotional Disturbance, Mental Retardation, Giftedness, English as a Second Language,BilingualEducation,andRegularEducation).
- Parent Educational Attainment (Less Than High School Degree,HighSchoolGraduateorEquivalent,SomeCollege or Technical School, Four or MoreYears of College).
The most challenging of stratification variables is socioeconomic status (SES), particularly because it tends to be associated with cognitive test performance and it is difficult to operationally define. Parent educational attainment is often used as an estimate of SES because it is readily available and objective, and because parent education correlates moderately with family income. Parent occupation and income are also sometimes combined as estimates of SES, although income information is generally difficult to obtain. Community estimates of SES add an additional level of sampling rigor, because the community in which an individual lives may be a greater factor in the child’s everyday life experience than his or her parents’ educational attainment. Similarly, the number of people residing in the home and the number of parents (one or two) heading the family are both factors that can influence a family’s socioeconomic condition. For example, a family of three that has an annual income of $40,000 may have more economic viability than a family of six that earns the same income. Also, a college-educated single parent may earn less income than two less educated cohabiting parents. The influences of SES on construct development clearly represent an area of further study, requiring more refined definition.
When test users intend to rank individuals relative to the special populations to which they belong, it may also be desirable to ensure that proportionate representation of those special populations are included in the normative sample (e.g., individuals who are mentally retarded, conduct disordered, or learning disabled). Millon, Davis, and Millon (1997) noted that tests normed on special populations may require the use of base rate scores rather than traditional standard scores, because assumptions of a normal distribution of scores often cannot be met within clinical populations.
Aclassic example of an inappropriate normative reference sample is found with the original Minnesota Multiphasic Personality Inventory (MMPI; Hathaway & McKinley, 1943), which was normed on 724 Minnesota white adults who were, for the most part, relatives or visitors of patients in the University of Minnesota Hospitals. Accordingly, the original MMPI reference group was primarily composed of Minnesota farmers! Fortunately, the MMPI-2 (Butcher, Dahlstrom, Graham, Tellegen, & Kaemmer, 1989) has remediated this normative shortcoming.
Appropriate Sampling Methodology
One of the principal objectives of sampling is to ensure that each individual in the target population has an equal and independent chance of being selected. Sampling methodologies include both probability and nonprobability approaches, which have different strengths and weaknesses in terms of accuracy, cost, and feasibility (Levy & Lemeshow, 1999).
Probability sampling is a random selection approach that permits the use of statistical theory to estimate the properties of sample estimators. Probability sampling is generally too expensive for norming educational and psychological tests, but it offers the advantage of permitting the determination of the degree of sampling error, such as is frequently reported with the results of most public opinion polls. Sampling error may be defined as the difference between a sample statistic and its corresponding population parameter. Sampling error is independent from measurement error and tends to have a systematic effect on test scores, whereas the effects of measurement error by definition is random. When sampling error in psychological test norms is not reported, the estimate of the true score will always be less accurate than when only measurement error is reported.
A probability sampling approach sometimes employed in psychological test norming is known as multistage stratified random cluster sampling; this approach uses a multistage sampling strategy in which a large or dispersed population is divided into a large number of groups, with participants in the groups selected via random sampling. In two-stage cluster sampling, each group undergoes a second round of simple random sampling based on the expectation that each cluster closely resembles every other cluster. For example, a set of schools may constitute the first stage of sampling, with students randomly drawn from the schools in the second stage. Cluster sampling is more economical than random sampling, but incremental amounts of error may be introduced at each stage of the sample selection. Moreover, cluster sampling commonly results in high standard errors when cases from a cluster are homogeneous (Levy & Lemeshow, 1999). Sampling error can be estimated with the cluster sampling approach, so long as the selection process at the various stages involves random sampling.
In general, sampling error tends to be largest when nonprobability-sampling approaches, such as convenience sampling or quota sampling, are employed. Convenience samples involve the use of a self-selected sample that is easily accessible (e.g., volunteers). Quota samples involve the selection by a coordinator of a predetermined number of cases with specific characteristics. The probability of acquiring an unrepresentative sample is high when using nonprobability procedures. The weakness of all nonprobability-sampling methods is that statistical theory cannot be used to estimate sampling precision, and accordingly sampling accuracy can only be subjectively evaluated (e.g., Kalton, 1983).
Adequately Sized Normative Samples
How large should a normative sample be? The number of participants sampled at any given stratification level needs to be sufficiently large to provide acceptable sampling error, stable parameter estimates for the target populations, and sufficient power in statistical analyses. As rules of thumb, group-administeredtestsgenerallysampleover10,000participants per age or grade level, whereas individually administered tests typically sample 100 to 200 participants per level (e.g., Robertson, 1992). In IRT, the minimum sample size is related to the choice of calibration model used. In an integrative review, Suen (1990) recommended that a minimum of 200 participants be examined for the one-parameter Rasch model, that at least 500 examinees be examined for the twoparameter model, and that at least 1,000 examinees be examined for the three-parameter model.
The minimum number of cases to be collected (or clusters to be sampled) also depends in part upon the sampling procedure used, and Levy and Lemeshow (1999) provide formulas for a variety of sampling procedures. Up to a point, the larger the sample, the greater the reliability of sampling accuracy. Cattell (1986) noted that eventually diminishing returns can be expected when sample sizes are increased beyond a reasonable level.
The smallest acceptable number of cases in a sampling plan may also be driven by the statistical analyses to be conducted. For example, Zieky (1993) recommended that a minimum of 500 examinees be distributed across the two groups compared in differential item function studies for groupadministered tests. For individually administered tests, these types of analyses require substantial oversampling of minorities.With regard to exploratory factor analyses, Riese,Waller, and Comrey (2000) have reviewed the psychometric literature and concluded that most rules of thumb pertaining to minimum sample size are not useful. They suggest that when communalities are high and factors are well defined, sample sizes of 100 are often adequate, but when communalities are low, the number of factors is large, and the number of indicators per factor is small, even a sample size of 500 may be inadequate. As with statistical analyses in general, minimal acceptable sample sizes should be based on practical considerations, including such considerations as desired alpha level, power, and effect size.
Sampling Precision
As we have discussed, sampling error cannot be formally estimated when probability sampling approaches are not used, and most educational and psychological tests do not employ probability sampling. Given this limitation, there are no objective standards for the sampling precision of test norms. Angoff (1984) recommended as a rule of thumb that the maximum tolerable sampling error should be no more than 14% of the standard error of measurement. He declined, however, to provide further guidance in this area: “Beyond the general consideration that norms should be as precise as their intended use demands and the cost permits, there is very little else that can be said regarding minimum standards for norms reliability” (p. 79).
In the absence of formal estimates of sampling error, the accuracy of sampling strata may be most easily determined by comparing stratification breakdowns against those available for the target population. The more closely the sample matches population characteristics, the more representative is a test’s normative sample. As best practice, we recommend that test developers provide tables showing the composition of the standardization sample within and across all stratification criteria (e.g., Percentages of the Normative Sample according to combined variables such as Age by Race by Parent Education). This level of stringency and detail ensures that important demographic variables are distributed proportionately across other stratifying variables according to population proportions. The practice of reporting sampling accuracy for single stratification variables “on the margins” (i.e., by one stratification variable at a time) tends to conceal lapses in sampling accuracy. For example, if sample proportions of low socioeconomic status are concentrated in minority groups (instead of being proportionately distributed across majority and minority groups), then the precision of the sample has been compromised through the neglect of minority groups with high socioeconomic status and majority groups with low socioeconomic status. The more the sample deviates from population proportions on multiple stratifications, the greater the effect of sampling error.
Manipulation of the sample composition to generate norms is often accomplished through sample weighting (i.e., application of participant weights to obtain a distribution of scores that is exactly proportioned to the target population representations). Weighting is more frequently used with group-administered educational tests than psychological tests because of the larger size of the normative samples. Educational tests typically involve the collection of thousands of cases, with weighting used to ensure proportionate representation. Weighting is less frequently used with psychological tests, and its use with these smaller samples may significantly affect systematic sampling error because fewer cases are collected and because weighting may thereby differentially affect proportions across different stratification criteria, improving one at the cost of another. Weighting is most likely to contribute to sampling error when a group has been inadequately represented with too few cases collected.
Recency of Sampling
How old can norms be and still remain accurate? Evidence from the last two decades suggests that norms from measures of cognitive ability and behavioral adjustment are susceptible to becoming soft or stale (i.e., test consumers should use older norms with caution). Use of outdated normative samples introduces systematic error into the diagnostic process and may negatively influence decision-making, such as by denying services (e.g., for mentally handicapping conditions) to sizable numbers of children and adolescents who otherwise would have been identified as eligible to receive services. Sample recency is an ethical concern for all psychologists who test or conduct assessments. The American Psychological Association’s (1992) Ethical Principles direct psychologists to avoid basing decisions or recommendations on results that stem from obsolete or outdated tests.
The problem of normative obsolescence has been most robustly demonstrated with intelligence tests. The Flynn effect (Herrnstein & Murray, 1994) describes a consistent pattern of population intelligence test score gains over time and across nations (Flynn, 1984, 1987, 1994, 1999). For intelligence tests, the rate of gain is about one third of an IQ point per year (3 points per decade), which has been a roughly uniform finding over time and for all ages (Flynn, 1999). The Flynn effect appears to occur as early as infancy (Bayley, 1993; S. K. Campbell, Siegel, Parr, & Ramey, 1986) and continues through the full range of adulthood (Tulsky & Ledbetter, 2000). The Flynn effect implies that older test norms may yield inflated scores relative to current normative expectations. For example, the Wechsler Intelligence Scale for Children—Revised (WISC-R; Wechsler, 1974) currently yields higher full scale IQs (FSIQs) than the WISC-III (Wechsler, 1991) by about 7 IQ points.
Systematic generational normative change may also occur in other areas of assessment. For example, parent and teacher reports on the Achenbach system of empirically based behavioral assessments show increased numbers of behavior problems and lower competence scores in the general population of children and adolescents from 1976 to 1989 (Achenbach & Howell, 1993). Just as the Flynn effect suggests a systematic increase in the intelligence of the general population over time, this effect may suggest a corresponding increase in behavioral maladjustment over time.
How often should tests be revised? There is no empirical basis for making a global recommendation, but it seems reasonable to conduct normative updates, restandardizations, or revisions at time intervals corresponding to the time expected to produce one standard error of measurement (SEM) of change. For example, given the Flynn effect and a WISC-III FSIQ SEM of 3.20, one could expect about 10 to 11 years should elapse before the test’s norms would soften to the magnitude of one SEM.
Calibration and Derivation of Reference Norms
In this section, several psychometric characteristics of test construction are described as they relate to building individual scales and developing appropriate norm-referenced scores. Calibration refers to the analysis of properties of gradation in a measure, defined in part by properties of test items. Norming is the process of using scores obtained by an appropriate sample to build quantitative Bibliography: that can be effectively used in the comparison and evaluation of individual performances relative to typical peer expectations.
Calibration
The process of item and scale calibration dates back to the earliest attempts to measure temperature. Early in the seventeenth century, there was no method to quantify heat and cold except through subjective judgment. Galileo and others experimented with devices that expanded air in glass as heat increased; use of liquid in glass to measure temperature was developed in the 1630s. Some two dozen temperature scales were available for use in Europe in the seventeenth century, and each scientist had his own scales with varying gradations and reference points. It was not until the early eighteenth century that more uniform scales were developed by Fahrenheit, Celsius, and de Réaumur.
The process of calibration has similarly evolved in psychological testing. In classical test theory, item difficulty is judged by the p value, or the proportion of people in the sample that passes an item. During ability test development, items are typically ranked by p value or the amount of the trait being measured. The use of regular, incremental increases in item difficulties provides a methodology for building scale gradations. Item difficulty properties in classical test theory are dependent upon the population sampled, so that a sample with higher levels of the latent trait (e.g., older children on a set of vocabulary items) would show different item properties (e.g., higher p values) than a sample with lower levels of the latent trait (e.g., younger children on the same set of vocabulary items).
In contrast, item response theory includes both item properties and levels of the latent trait in analyses, permitting item calibration to be sample-independent. The same item difficulty and discrimination values will be estimated regardless of trait distribution. This process permits item calibration to be “sample-free,” according to Wright (1999), so that the scale transcends the group measured. Embretson (1999) has stated one of the new rules of measurement as “Unbiased estimates of item properties may be obtained from unrepresentative samples” (p. 13).
Item response theory permits several item parameters to be estimated in the process of item calibration. Among the indexes calculated in widely used Rasch model computer programs (e.g., Linacre & Wright, 1999) are item fit-to-model expectations, item difficulty calibrations, item-total correlations, and item standard error. The conformity of any item to expectations from the Rasch model may be determined by examining item fit. Items are said to have good fits with typical item characteristic curves when they show expected patterns near to and far from the latent trait level for which they are the best estimates. Measures of item difficulty adjusted for the influence of sample ability are typically expressed in logits, permitting approximation of equal difficulty intervals.
Item and Scale Gradients
The item gradient of a test refers to how steeply or gradually items are arranged by trait level and the resulting gaps that may ensue in standard scores. In order for a test to have adequate sensitivity to differing degrees of ability or any trait being measured, it must have adequate item density across the distribution of the latent trait. The larger the resulting standard score differences in relation to a change in a single raw score point, the less sensitive, discriminating, and effective a test is.
For example, on the Memory subtest of the Battelle Developmental Inventory (Newborg, Stock, Wnek, Guidubaldi, & Svinicki, 1984), a child who is 1 year, 11 months old who earned a raw score of 7 would have performance ranked at the 1st percentile for age, whereas a raw score of 8 leaps to a percentile rank of 74. The steepness of this gradient in the distribution of scores suggests that this subtest is insensitive to even large gradations in ability at this age.
A similar problem is evident on the Motor Quality index of the Bayley Scales of Infant Development–Second Edition Behavior Rating Scale (Bayley, 1993). A 36-month-old child with a raw score rating of 39 obtains a percentile rank of 66. The same child obtaining a raw score of 40 is ranked at the 99th percentile.
As a recommended guideline, tests may be said to have adequate item gradients and item density when there are approximately three items per Rasch logit, or when passage of a single item results in a standard score change of less than one third standard deviation (0.33 SD) (Bracken, 1987; Bracken & McCallum, 1998). Items that are not evenly distributed in terms of the latent trait may yield steeper change gradients that will decrease the sensitivity of the instrument to finer gradations in ability.
Floor and Ceiling Effects
Do tests have adequate breadth, bottom and top? Many tests yield their most valuable clinical inferences when scores are extreme (i.e., very low or very high). Accordingly, tests used for clinical purposes need sufficient discriminating power in the extreme ends of the distributions.
The floor of a test represents the extent to which an individual can earn appropriately low standard scores. For example, an intelligence test intended for use in the identification of individuals diagnosed with mental retardation must, by definition, extend at least 2 standard deviations below normative expectations (IQ < 70). In order to serve individuals with severe to profound mental retardation, test scores must extend even further to more than 4 standard deviations below the normative mean (IQ < 40). Tests without a sufficiently low floor would not be useful for decision-making for more severe forms of cognitive impairment.
A similar situation arises for test ceiling effects. An intelligence test with a ceiling greater than 2 standard deviations above the mean (IQ > 130) can identify most candidates for intellectually gifted programs. To identify individuals as exceptionally gifted (i.e., IQ > 160), a test ceiling must extend more than 4 standard deviations above normative expectations. There are several unique psychometric challenges to extending norms to these heights, and most extended norms are extrapolations based upon subtest scaling for higher ability samples (i.e., older examinees than those within the specified age band).
As a rule of thumb, tests used for clinical decision-making should have floors and ceilings that differentiate the extreme lowest and highest 2% of the population from the middlemost 96% (Bracken, 1987, 1988; Bracken & McCallum, 1998). Tests with inadequate floors or ceilings are inappropriate for assessing children with known or suspected mental retardation, intellectual giftedness, severe psychopathology, or exceptional social and educational competencies.
Derivation of Norm-Referenced Scores
Item response theory yields several different kinds of interpretable scores (e.g., Woodcock, 1999), only some of which are norm-referenced standard scores. Because most test users are most familiar with the use of standard scores, it is the process of arriving at this type of score that we discuss. Transformation of raw scores to standard scores involves a number of decisions based on psychometric science and more than a little art.
The first decision involves the nature of raw score transformations, based upon theoretical considerations (Is the trait being measured thought to be normally distributed?) and examination of the cumulative frequency distributions of raw scores within age groups and across age groups. The objective of this transformation is to preserve the shape of the raw score frequency distribution, including mean, variance, kurtosis, and skewness. Linear transformations of raw scores are based solely on the mean and distribution of raw scores and are commonly used when distributions are not normal; linear transformation assumes that the distances between scale points reflect true differences in the degree of the measured trait present. Area transformations of raw score distributions convert the shape of the frequency distribution into a specified type of distribution. When the raw scores are normally distributed, then they may be transformed to fit a normal curve, with corresponding percentile ranks assigned in a way so that the mean corresponds to the 50th percentile, – 1 SD and + 1 SD correspond to the 16th and 84th percentiles, respectively, and so forth. When the frequency distribution is not normal, it is possible to select from varying types of nonnormal frequency curves (e.g., Johnson, 1949) as a basis for transformation of raw scores, or to use polynomial curve fitting equations.
Following raw score transformations is the process of smoothing the curves. Data smoothing typically occurs within groups and across groups to correct for minor irregularities, presumably those irregularities that result from sampling fluctuations and error. Quality checking also occurs to eliminate vertical reversals (such as those within an age group, from one raw score to the next) and horizonal reversals (such as those within a raw score series, from one age to the next). Smoothing and elimination of reversals serve to ensure that raw score to standard score transformations progress according to growth and maturation expectations for the trait being measured.
Test Score Validity
Validity is about the meaning of test scores (Cronbach & Meehl, 1955). Although a variety of narrower definitions have been proposed, psychometric validity deals with the extent to which test scores exclusively measure their intended psychological construct(s) and guide consequential decisionmaking. This concept represents something of a metamorphosis in understanding test validation because of its emphasis on the meaning and application of test results (Geisinger, 1992). Validity involves the inferences made from test scores and is not inherent to the test itself (Cronbach, 1971).
Evidence of test score validity may take different forms, many of which are detailed below, but they are all ultimately concerned with construct validity (Guion, 1977; Messick, 1995a, 1995b). Construct validity involves appraisal of a body of evidence determining the degree to which test score inferences are accurate, adequate, and appropriate indicators of the examinee’s standing on the trait or characteristic measured by the test. Excessive narrowness or broadness in the definition and measurement of the targeted construct can threaten construct validity. The problem of excessive narrowness, or construct underrepresentation, refers to the extent to which test scores fail to tap important facets of the construct being measured. The problem of excessive broadness, or construct irrelevance, refers to the extent to which test scores are influenced by unintended factors, including irrelevant constructs and test procedural biases.
Construct validity can be supported with two broad classes of evidence: internal and external validation, which parallel the classes of threats to validity of research designs (D. T. Campbell & Stanley, 1963; Cook & Campbell, 1979). Internal evidence for validity includes information intrinsic to the measure itself, including content, substantive, and structural validation. External evidence for test score validity may be drawn from research involving independent, criterion-related data. External evidence includes convergent, discriminant, criterion-related, and consequential validation. This internalexternal dichotomy with its constituent elements represents a distillation of concepts described by Anastasi and Urbina (1997), Jackson (1971), Loevinger (1957), Messick (1995a, 1995b), and Millon et al. (1997), among others.
Internal Evidence of Validity
Internalsourcesofvalidityincludetheintrinsiccharacteristics of a test, especially its content, assessment methods, structure, and theoretical underpinnings. In this section, several sources of evidence internal to tests are described, including content validity, substantive validity, and structural validity.
Content Validity
Content validity is the degree to which elements of a test, ranging from items to instructions, are relevant to and representative of varying facets of the targeted construct (Haynes, Richard, & Kubany, 1995). Content validity is typically established through the use of expert judges who review test content, but other procedures may also be employed (Haynes et al., 1995). Hopkins and Antes (1978) recommended that tests include a table of content specifications, in which the facets and dimensions of the construct are listed alongside the number and identity of items assessing each facet.
Content differences across tests purporting to measure the same construct can explain why similar tests sometimes yield dissimilar results for the same examinee (Bracken, 1988). For example, the universe of mathematical skills includes varying types of numbers (e.g., whole numbers, decimals, fractions), number concepts (e.g., half, dozen, twice, more than), and basic operations (addition, subtraction, multiplication, division). The extent to which tests differentially sample content can account for differences between tests that purport to measure the same construct.
Tests should ideally include enough diverse content to adequately sample the breadth of construct-relevant domains, but content sampling should not be so diverse that scale coherence and uniformity are lost. Construct underrepresentation, stemming from use of narrow and homogeneous content sampling, tends to yield higher reliabilities than tests with heterogeneous item content, at the potential cost of generalizability and external validity. In contrast, tests with more heterogeneous content may show higher validity with the concomitant cost of scale reliability. Clinical inferences made from tests with excessively narrow breadth of content may be suspect, even when other indexes of validity are satisfactory (Haynes et al., 1995).
Substantive Validity
The formulation of test items and procedures based on and consistent with a theory has been termed substantive validity (Loevinger, 1957). The presence of an underlying theory enhances a test’s construct validity by providing a scaffolding between content and constructs, which logically explains relations between elements, predicts undetermined parameters, and explains findings that would be anomalous within another theory (e.g., Kuhn, 1970). As Crocker and Algina (1986) suggest, “psychological measurement, even though it is based on observable responses, would have little meaning or usefulness unless it could be interpreted in light of the underlying theoretical construct” (p. 7).
Many major psychological tests remain psychometrically rigorous but impoverished in terms of theoretical underpinnings. For example, there is conspicuously little theory associated with most widely used measures of intelligence (e.g., the Wechsler scales), behavior problems (e.g., the Child Behavior Checklist), neuropsychological functioning (e.g., the Halstead-Reitan Neuropsychology Battery), and personality and psychopathology (the MMPI-2). There may be some post hoc benefits to tests developed without theories; as observed by Nunnally and Bernstein (1994), “Virtually every measure that became popular led to new unanticipated theories” (p. 107).
Personality assessment has taken a leading role in theorybased test development, while cognitive-intellectual assessment has lagged. Describing best practices for the measurement of personality some three decades ago, Loevinger (1972) commented, “Theory has always been the mark of a mature science. The time is overdue for psychology, in general, and personality measurement, in particular, to come of age” (p. 56). In the same year, Meehl (1972) renounced his former position as a “dustbowl empiricist” in test development:
I now think that all stages in personality test development, from initial phase of item pool construction to a late-stage optimized clinical interpretive procedure for the fully developed and “validated” instrument, theory—and by this I mean all sorts of theory, including trait theory, developmental theory, learning theory, psychodynamics, and behavior genetics—should play an important role. . . . [P]sychology can no longer afford to adopt psychometric procedures whose methodology proceeds with almost zero reference to what bets it is reasonable to lay upon substantive personological horses. (pp. 149–151)
Leading personality measures with well-articulated theories include the “Big Five” factors of personality and Millon’s “three polarity” bioevolutionary theory. Newer intelligence tests based on theory such as the Kaufman Assessment Battery for Children (Kaufman & Kaufman, 1983) and Cognitive Assessment System (Naglieri & Das, 1997) represent evidence of substantive validity in cognitive assessment.
Structural Validity
Structural validity relies mainly on factor analytic techniques to identify a test’s underlying dimensions and the variance associated with each dimension. Also called factorial validity (Guilford, 1950), this form of validity may utilize other methodologies such as multidimensional scaling to help researchers understand a test’s structure. Structural validity evidence is generally internal to the test, based on the analysis of constituent subtests or scoring indexes. Structural validation approaches may also combine two or more instruments in cross-battery factor analyses to explore evidence of convergent validity.
The two leading factor-analytic methodologies used to establish structural validity are exploratory and confirmatory factor analyses. Exploratory factor analyses allow for empirical derivation of the structure of an instrument, often without a priori expectations, and are best interpreted according to the psychological meaningfulness of the dimensions or factors that emerge (e.g., Gorsuch, 1983). Confirmatory factor analyses help researchers evaluate the congruence of the test data with a specified model, as well as measuring the relative fit of competing models. Confirmatory analyses explore the extent to which the proposed factor structure of a test explains its underlying dimensions as compared to alternative theoretical explanations.
As a recommended guideline, the underlying factor structure of a test should be congruent with its composite indexes (e.g., Floyd & Widaman, 1995), and the interpretive structure of a test should be the best fitting model available. For example, several interpretive indexes for the Wechsler Intelligence Scales (i.e., the verbal comprehension, perceptual organization, working memory/freedom from distractibility, and processing speed indexes) match the empirical structure suggested by subtest-level factor analyses; however, the original Verbal–Performance Scale dichotomy has never been supported unequivocally in factor-analytic studies. At the same time, leading instruments such as the MMPI-2 yield clinical symptom-based scales that do not match the structure suggested by item-level factor analyses. Several new instruments with strong theoretical underpinnings have been criticized for mismatch between factor structure and interpretive structure (e.g., Keith & Kranzler, 1999; Stinnett, Coombs, Oehler-Stinnett, Fuqua, & Palmer, 1999) even when there is a theoretical and clinical rationale for scale composition. A reasonable balance should be struck between theoretical underpinnings and empirical validation; that is, if factor analysis does not match a test’s underpinnings, is that the fault of the theory, the factor analysis, the nature of the test, or a combination of these factors? Carroll (1983), whose factoranalytic work has been influential in contemporary cognitive assessment, cautioned against overreliance on factor analysis as principal evidence of validity, encouraging use of additional sources of validity evidence that move beyond factor analysis (p. 26). Consideration and credit must be given to both theory and empirical validation results, without one taking precedence over the other.
External Evidence of Validity
Evidenceoftestscorevalidityalsoincludestheextenttowhich the test results predict meaningful and generalizable behaviors independent of actual test performance. Test results need to be validated for any intended application or decision-making process in which they play a part. In this section, external classes of evidence for test construct validity are described, including convergent, discriminant, criterion-related, and consequentialvalidity,aswellasspecializedformsofvaliditywithin these categories.
Convergent and Discriminant Validity
In a frequently cited 1959 article, D. T. Campbell and Fiske described a multitrait-multimethod methodology for investigating construct validity. In brief, they suggested that a measure is jointly defined by its methods of gathering data (e.g., self-report or parent-report) and its trait-related content (e.g., anxiety or depression). They noted that test scores should be related to (i.e., strongly correlated with) other measures of the same psychological construct (convergent evidence of validity) and comparatively unrelated to (i.e., weakly correlated with) measures of different psychological constructs (discriminant evidence of validity). The multitraitmultimethod matrix allows for the comparison of the relative strength of association between two measures of the same trait using different methods (monotrait-heteromethod correlations), two measures with a common method but tapping different traits (heterotrait-monomethod correlations), and two measures tapping different traits using different methods (heterotrait-heteromethod correlations), all of which are expected to yield lower values than internal consistency reliability statistics using the same method to tap the same trait.
The multitrait-multimethod matrix offers several advantages, such as the identification of problematic method variance. Method variance is a measurement artifact that threatens validity by producing spuriously high correlations between similar assessment methods of different traits. For example, high correlations between digit span, letter span, phoneme span, and word span procedures might be interpreted as stemming from the immediate memory span recall method common to all the procedures rather than any specific abilities being assessed. Method effects may be assessed by comparing the correlations of different traits measured with the same method (i.e., monomethod correlations) and the correlations among different traits across methods (i.e., heteromethod correlations). Method variance is said to be present if the heterotrait-monomethod correlations greatly exceed the heterotrait-heteromethod correlations in magnitude, assuming that convergent validity has been demonstrated.
Fiske and Campbell (1992) subsequently recognized shortcomings in their methodology: “We have yet to see a really good matrix: one that is based on fairly similar concepts and plausibly independent methods and shows high convergent and discriminant validation by all standards” (p. 394). At the same time, the methodology has provided a useful framework for establishing evidence of validity.
Criterion-Related Validity
How well do test scores predict performance on independent criterion measures and differentiate criterion groups? The relationship of test scores to relevant external criteria constitutes evidence of criterion-related validity, which may take several different forms. Evidence of validity may include criterion scores that are obtained at about the same time (concurrent evidence of validity) or criterion scores that are obtained at some future date (predictive evidence of validity). External criteria may also include functional, real-life variables (ecological validity), diagnostic or placement indexes (diagnostic validity), and intervention-related approaches (treatment validity).
The emphasis on understanding the functional implications of test findings has been termed ecological validity (Neisser, 1978). Banaji and Crowder (1989) suggested, “If research is scientifically sound it is better to use ecologically lifelike rather than contrived methods” (p. 1188). In essence, ecological validation efforts relate test performance to various aspects of person-environment functioning in everyday life, including identification of both competencies and deficits in social and educational adjustment. Test developers should show the ecological relevance of the constructs a test purports to measure, as well as the utility of the test for predicting everyday functional limitations for remediation. In contrast, tests based on laboratory-like procedures with little or no discernible relevance to real life may be said to have little ecological validity.
The capacity of a measure to produce relevant applied group differences has been termed diagnostic validity (e.g., Ittenbach, Esters, & Wainer, 1997). When tests are intended for diagnostic or placement decisions, diagnostic validity refers to the utility of the test in differentiating the groups of concern. The process of arriving at diagnostic validity may be informed by decision theory, a process involving calculations of decision-making accuracy in comparison to the base rate occurrence of an event or diagnosis in a given population. Decision theory has been applied to psychological tests (Cronbach & Gleser, 1965) and other high-stakes diagnostic tests (Swets, 1992) and is useful for identifying the extent to which tests improve clinical or educational decision-making.
The method of contrasted groups is a common methodology to demonstrate diagnostic validity. In this methodology, test performance of two samples that are known to be different on the criterion of interest is compared. For example, a test intended to tap behavioral correlates of anxiety should show differences between groups of normal individuals and individuals diagnosed with anxiety disorders. A test intended for differential diagnostic utility should be effective in differentiating individuals with anxiety disorders from diagnoses that appear behaviorally similar. Decision-making classification accuracy may be determined by developing cutoff scores or rules to differentiate the groups, so long as the rules show adequate sensitivity, specificity, positive predictive power, and negative predictive power. These terms may be defined as follows:
- Sensitivity: the proportion of cases in which a clinical condition is detected when it is in fact present (true positive).
- Specificity: the proportion of cases for which a diagnosis is rejected, when rejection is in fact warranted (true negative).
- Positive predictive power: the probability of having the diagnosis given that the score exceeds the cutoff score.
- Negative predictive power: the probability of not having the diagnosis given that the score does not exceed the cutoff score.
All of these indexes of diagnostic accuracy are dependent upon the prevalence of the disorder and the prevalence of the score on either side of the cut point.
Findings pertaining to decision-making should be interpreted conservatively and cross-validated on independent samples because (a) classification decisions should in practice be based upon the results of multiple sources of information rather than test results from a single measure, and (b) the consequences of a classification decision should be considered in evaluating the impact of classification accuracy. A false negative classification, in which a child is incorrectly classified as not needing special education services, could mean the denial of needed services to a student. Alternately, a false positive classification, in which a typical child is recommended for special services, could result in a child’s being labeled unfairly.
Treatment validity refers to the value of an assessment in selecting and implementing interventions and treatments that will benefit the examinee. “Assessment data are said to be treatmentvalid,”commentedBarrios(1988),“iftheyexpedite the orderly course of treatment or enhance the outcome of treatment” (p. 34). Other terms used to describe treatment validity are treatment utility (Hayes, Nelson, & Jarrett, 1987) and rehabilitation-referenced assessment (Heinrichs, 1990).
Whether the stated purpose of clinical assessment is description, diagnosis, intervention, prediction, tracking, or simply understanding, its ultimate raison d’être is to select and implement services in the best interests of the examinee, that is, to guide treatment. In 1957, Cronbach described a rationale for linking assessment to treatment: “For any potential problem, there is some best group of treatments to use and best allocation of persons to treatments” (p. 680).
The origins of treatment validity may be traced to the concept of aptitude by treatment interactions (ATI) originally proposed by Cronbach (1957), who initiated decades of research seeking to specify relationships between the traits measured by tests and the intervention methodology used to produce change. In clinical practice, promising efforts to match client characteristics and clinical dimensions to preferred therapist characteristics and treatment approaches have been made (e.g., Beutler & Clarkin, 1990; Beutler & Harwood, 2000; Lazarus, 1973; Maruish, 1999), but progress has been constrained in part by difficulty in arriving at consensus for empirically supported treatments (e.g., Beutler, 1998). In psychoeducational settings, test results have been shown to have limited utility in predicting differential responses to varied forms of instruction (e.g., Reschly, 1997). It is possible that progress in educational domains has been constrained by underestimation of the complexity of treatment validity. For example, many ATI studies utilize overly simple modalityspecific dimensions (auditory-visual learning style or verbalnonverbal pBibliography:) because of their easy appeal.
Consequential Validity
In recent years, there has been an increasing recognition that test usage has both intended and unintended effects on individuals and groups. Messick (1989, 1995b) has argued that test developers must understand the social values intrinsic to the purposes and application of psychological tests, especially those that may act as a trigger for social and educational actions. Linn (1998) has suggested that when governmental bodies establish policies that drive test development and implementation, the responsibility for the consequences of test usage must also be borne by the policymakers. In this context, consequential validity refers to the appraisal of value implications and the social impact of score interpretation as a basis for action and labeling, as well as the actual and potential consequences of test use (Messick, 1989; Reckase, 1998).
This new form of validity represents an expansion of traditional conceptualizations of test score validity. Lees-Haley (1996) has urged caution about consequential validity, noting its potential for encouraging the encroachment of politics into science. The Standards for Educational and Psychological Testing (1999) recognize but carefully circumscribe consequential validity:
Evidence about consequences may be directly relevant to validity when it can be traced to a source of invalidity such as construct underrepresentation or construct-irrelevant components. Evidence about consequences that cannot be so traced—that in fact reflects valid differences in performance—is crucial in informing policy decisions but falls outside the technical purview of validity. (p. 16)
Evidence of consequential validity may be collected by test developers during a period starting early in test development and extending through the life of the test (Reckase, 1998). For educational tests, surveys and focus groups have been described as two methodologies to examine consequential aspects of validity (Chudowsky & Behuniak, 1998; Pomplun, 1997). As the social consequences of test use and interpretation are ascertained, the development and determinants of the consequences need to be explored. A measure with unintended negative side effects calls for examination of alternative measures and assessment counterproposals. Consequential validity is especially relevant to issues of bias, fairness, and distributive justice.
Validity Generalization
The accumulation of external evidence of test validity becomes most important when test results are generalized across contexts, situations, and populations, and when the consequences of testing reach beyond the test’s original intent. According to Messick (1995b), “The issue of generalizability of score inferences across tasks and contexts goes to the very heart of score meaning. Indeed, setting the boundaries of score meaning is precisely what generalizability evidence is meant to address” (p. 745).
Hunter and Schmidt (1990; Hunter, Schmidt, & Jackson, 1982; Schmidt & Hunter, 1977) developed a methodology of validity generalization, a form of meta-analysis, that analyzes the extent to which variation in test validity across studies is due to sampling error or other sources of error such as imperfect reliability, imperfect construct validity, range restriction, or artificial dichotomization. Once incongruent or conflictual findings across studies can be explained in terms of sources of error, meta-analysis enables theory to be tested, generalized, and quantitatively extended.
Test Score Reliability
If measurement is to be trusted, it must be reliable. It must be consistent, accurate, and uniform across testing occasions, across time, across observers, and across samples. In psychometric terms, reliability refers to the extent to which measurement results are precise and accurate, free from random and unexplained error. Test score reliability sets the upper limit of validity and thereby constrains test validity, so that unreliable test scores cannot be considered valid.
Reliability has been described as “fundamental to all of psychology” (Li, Rosenthal, & Rubin, 1996), and its study dates back nearly a century (Brown, 1910; Spearman, 1910).
Concepts of reliability in test theory have evolved, including emphasis in IRT models on the test information function as an advancement over classical models (e.g., Hambleton et al., 1991) and attempts to provide new unifying and coherent models of reliability (e.g., Li & Wainer, 1997). For example, Embretson (1999) challenged classical test theory tradition by asserting that “Shorter tests can be more reliable than longer tests” (p. 12) and that “standard error of measurement differs between persons with different response patterns but generalizes across populations” (p. 12). In this section, reliability is described according to classical test theory and item response theory. Guidelines are provided for the objective evaluation of reliability.
Internal Consistency
Determination of a test’s internal consistency addresses the degree of uniformity and coherence among its constituent parts. Tests that are more uniform tend to be more reliable. As a measure of internal consistency, the reliability coefficient is the square of the correlation between obtained test scores and true scores; it will be high if there is relatively little error but low with a large amount of error. In classical test theory, reliability is based on the assumption that measurement error is distributed normally and equally for all score levels. By contrast, item response theory posits that reliability differs between persons with different response patterns and levels of ability but generalizes across populations (Embretson & Hershberger, 1999).
Several statistics are typically used to calculate internal consistency. The split-half method of estimating reliability effectively splits test items in half (e.g., into odd items and even items) and correlates the score from each half of the test with the score from the other half. This technique reduces the number of items in the test, thereby reducing the magnitude of the reliability. Use of the Spearman-Brown prophecy formula permits extrapolation from the obtained reliability coefficient to original length of the test, typically raising the reliability of the test. Perhaps the most common statistical index of internal consistency is Cronbach’s alpha, which provides a lower bound estimate of test score reliability equivalent to the average split-half consistency coefficient for all possible divisions of the test into halves. Note that item response theory implies that under some conditions (e.g., adaptive testing, in which the items closest to an examinee’s ability level need be measured) short tests can be more reliable than longer tests (e.g., Embretson, 1999).
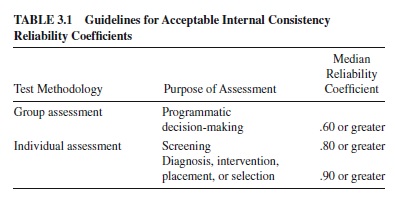
In general, minimal levels of acceptable reliability should be determined by the intended application and likely consequences of test scores. Several psychometricians have proposed guidelines for the evaluation of test score reliability coefficients (e.g., Bracken, 1987; Cicchetti, 1994; Clark & Watson, 1995; Nunnally & Bernstein, 1994; Salvia & Ysseldyke, 2001), depending upon whether test scores are to be used for high- or low-stakes decision-making. High-stakes tests refer to tests that have important and direct consequences such as clinical-diagnostic, placement, promotion, personnel selection, or treatment decisions; by virtue of their gravity, these tests require more rigorous and consistent psychometric standards. Low-stakes tests, by contrast, tend to have only minor or indirect consequences for examinees.
After a test meets acceptable guidelines for minimal acceptable reliability, there are limited benefits to furtheri ncreasing reliability. Clark and Watson (1995) observe that “Maximizing internal consistency almost invariably produces a scale that is quite narrow in content; if the scale is narrower than the target construct, it svalidity is compromised” (pp.316–317). Nunnally and Bernstein (1994, p. 265) state more directly: “Never switch to a less valid measure simply because it is more reliable.”
Local Reliability and Conditional Standard Error
Internal consistency indexes of reliability provide a single average estimate of measurement precision across the full range of test scores. In contrast, local reliability refers to measurement precision at specified trait levels or ranges of scores. Conditional error refers to the measurement variance at a particular level of the latent trait, and its square root is a conditional standard error. Whereas classical test theory posits that the standard error of measurement is constant and applies to all scores in a particular population, item response theory posits that the standard error of measurement varies according to the test scores obtained by the examinee but generalizes across populations (Embretson & Hershberger, 1999).
As an illustration of the use of classical test theory in the determination of local reliability, the Universal Nonverbal Intelligence Test (UNIT; Bracken & McCallum, 1998) presents local reliabilities from a classical test theory orientation. Based on the rationale that a common cut score for classification of individuals as mentally retarded is an FSIQ equal to 70, the reliability of test scores surrounding that decision point was calculated. Specifically, coefficient alpha reliabilities were calculated for FSIQs from – 1.33 and – 2.66 standard deviations below the normative mean. Reliabilities were corrected for restriction in range, and results showed that composite IQ reliabilities exceeded the .90 suggested criterion. That is, the UNIT is sufficiently precise at this ability range to reliably identify individual performance near to a common cut point for classification as mentally retarded.
Item response theory permits the determination of conditional standard error at every level of performance on a test. Several measures, such as the Differential Ability Scales (Elliott, 1990) and the Scales of Independent Behavior— Revised (SIB-R; Bruininks, Woodcock, Weatherman, & Hill, 1996), report local standard errors or local reliabilities for every test score. This methodology not only determines whether a test is more accurate for some members of a group (e.g., high-functioning individuals) than for others (Daniel, 1999), but also promises that many other indexes derived from reliability indexes (e.g., index discrepancy scores) may eventually become tailored to an examinee’s actual performance. Several IRT-based methodologies are available for estimating local scale reliabilities using conditional standard errors of measurement (Andrich, 1988; Daniel, 1999; Kolen, Zeng, & Hanson, 1996; Samejima, 1994), but none has yet become a test industry standard.
Temporal Stability
Are test scores consistent over time? Test scores must be reasonably consistent to have practical utility for making clinical and educational decisions and to be predictive of future performance. The stability coefficient, or test-retest score reliability coefficient, is an index of temporal stability that can be calculated by correlating test performance for a large number of examinees at two points in time. Two weeks is considered a preferred test-retest time interval (Nunnally & Bernstein, 1994; Salvia & Ysseldyke, 2001), because longer intervals increase the amount of error (due to maturation and learning) and tend to lower the estimated reliability.
Bracken (1987; Bracken & McCallum, 1998) recommends that a total test stability coefficient should be greater than or equal to .90 for high-stakes tests over relatively short test-retest intervals, whereas a stability coefficient of .80 is reasonable for low-stakes testing. Stability coefficients may be spuriously high, even with tests with low internal consistency, but tests with low stability coefficients tend to have low internal consistency unless they are tapping highly variable state-based constructs such as state anxiety (Nunnally & Bernstein, 1994). As a general rule of thumb, measures of internal consistency are preferred to stability coefficients as indexes of reliability.
Interrater Consistency and Consensus
Whenever tests require observers to render judgments, ratings, or scores for a specific behavior or performance, the consistency among observers constitutes an important source of measurement precision. Two separate methodological approaches have been utilized to study consistency and consensus among observers: interrater reliability (using correlational indexes to reference consistency among observers) and interrater agreement (addressing percent agreement among observers; e.g., Tinsley & Weiss, 1975). These distinctive approaches are necessary because it is possible to have high interrater reliability with low manifest agreement among raters if ratings are different but proportional. Similarly, it is possible to have low interrater reliability with high manifest agreement among raters if consistency indexes lack power because of restriction in range.
Interrater reliability refers to the proportional consistency of variance among raters and tends to be correlational. The simplest index involves correlation of total scores generated by separate raters. The intraclass correlation is another index of reliability commonly used to estimate the reliability of ratings. Its value ranges from 0 to 1.00, and it can be used to estimate the expected reliability of either the individual ratings provided by a single rater or the mean rating provided by a group of raters (Shrout & Fleiss, 1979). Another index of reliability, Kendall’s coefficient of concordance, establishes how much reliability exists among ranked data. This procedure is appropriate when raters are asked to rank order the persons or behaviors along a specified dimension.
Interrater agreement refers to the interchangeability of judgments among raters, addressing the extent to which raters make the same ratings. Indexes of interrater agreement typically estimate percentage of agreement on categorical and rating decisions among observers, differing in the extent to which they are sensitive to degrees of agreement correct for chance agreement. Cohen’s kappa is a widely used statistic of interobserver agreement intended for situations in which raters classify the items being rated into discrete, nominal categories. Kappa ranges from – 1.00 to +1.00; kappa values of .75 or higher are generally taken to indicate excellent agreement beyond chance, values between .60 and .74 are considered good agreement, those between .40 and .59 are considered fair, and those below .40 are considered poor (Fleiss, 1981).
Interrater reliability and agreement may vary logically depending upon the degree of consistency expected from specific sets of raters. For example, it might be anticipated that people who rate a child’s behavior in different contexts (e.g., school vs. home) would produce lower correlations than two raters who rate the child within the same context (e.g., two parents within the home or two teachers at school). In a review of 13 preschool social-emotional instruments, the vast majority of reported coefficients of interrater congruence were below .80 (range .12 to .89). Walker and Bracken (1996) investigated the congruence of biological parents who rated their children on four preschool behavior rating scales. Interparent congruence ranged from a low of .03 (Temperament Assessment Battery for Children Ease of Management through Distractibility) to a high of .79 (Temperament Assessment Battery for Children Approach/Withdrawal). In addition to concern about low congruence coefficients, the authors voiced concern that 44% of the parent pairs had a mean discrepancy across scales of 10 to 13 standard score points; differences ranged from 0 to 79 standard score points.
Interrater studies are preferentially conducted under field conditions, to enhance generalizability of testing by clinicians “performing under the time constraints and conditions of their work” (Wood, Nezworski, & Stejskal, 1996, p. 4). Cone (1988) has described interscorer studies as fundamental to measurement, because without scoring consistency and agreement, many other reliability and validity issues cannot be addressed.
Congruence Between Alternative Forms
When two parallel forms of a test are available, then correlating scores on each form provides another way to assess reliability. In classical test theory, strict parallelism between forms requires equality of means, variances, and covariances (Gulliksen, 1950). A hierarchy of methods for pinpointing sources of measurement error with alternative forms has been proposed (Nunnally & Bernstein, 1994; Salvia & Ysseldyke, 2001): (a) assess alternate-form reliability with a two-week interval between forms, (b) administer both forms on the same day, and if necessary (c) arrange for different raters to score the forms administered with a two-week retest interval and on the same day. If the score correlation over the twoweek interval between the alternative forms is lower than coefficient alpha by .20 or more, then considerable measurement error is present due to internal consistency, scoring subjectivity, or trait instability over time. If the score correlation is substantially higher for forms administered on the same day, then the error may stem from trait variation over time. If the correlations remain low for forms administered on the same day, then the two forms may differ in content with one form being more internally consistent than the other. If trait variation and content differences have been ruled out, then comparison of subjective ratings from different sources may permit the major source of error to be attributed to the subjectivity of scoring.
In item response theory, test forms may be compared by examining the forms at the item level. Forms with items of comparable item difficulties, response ogives, and standard errors by trait level will tend to have adequate levels of alternate form reliability (e.g., McGrew & Woodcock, 2001). For example, when item difficulties for one form are plotted against those for the second form, a clear linear trend is expected. When raw scores are plotted against trait levels for the two forms on the same graph, the ogive plots should be identical.
At the same time, scores from different tests tapping the same construct need not be parallel if both involve sets of itemsthatareclosetotheexaminee’sabilitylevel.Asreported by Embretson (1999), “Comparing test scores across multiple forms is optimal when test difficulty levels vary across persons” (p. 12).The capacity of IRTto estimate trait level across differing tests does not require assumptions of parallel forms or test equating.
Reliability Generalization
Reliability generalization is a meta-analytic methodology that investigates the reliability of scores across studies and samples (Vacha-Haase, 1998). An extension of validity generalization (Hunter & Schmidt, 1990; Schmidt & Hunter, 1977), reliability generalization investigates the stability of reliability coefficients across samples and studies. In order to demonstrate measurement precision for the populations for which a test is intended, the test should show comparable levels of reliability across various demographic subsets of the population (e.g., gender, race, ethnic groups), as well as salient clinical and exceptional populations.
Test Score Fairness
From the inception of psychological testing, problems with racial, ethnic, and gender bias have been apparent.As early as 1911, Alfred Binet (Binet & Simon, 1911/1916) was aware that a failure to represent diverse classes of socioeconomic status would affect normative performance on intelligence tests. He deleted classes of items that related more to quality of education than to mental faculties. Early editions of the Stanford-Binet and the Wechsler intelligence scales were standardized on entirelyWhite, native-born samples (Terman, 1916; Terman & Merrill, 1937; Wechsler, 1939, 1946, 1949). In addition to sample limitations, early tests also contained items that reflected positively on whites. Early editions of the Stanford-Binet included an Aesthetic Comparisons item in which examinees were shown a white, well-coiffed blond woman and a disheveled woman with African features; the examinee was asked “Which one is prettier?” The original MMPI (Hathaway & McKinley, 1943) was normed on a convenience sample of white adult Minnesotans and contained true-false, self-report items referring to culturespecific games (drop-the-handkerchief), literature (Alice in Wonderland), and religious beliefs (the second coming of Christ). These types of problems, of normative samples without minority representation and racially and ethnically insensitive items, are now routinely avoided by most contemporary test developers.
In spite of these advances, the fairness of educational and psychological tests represents one of the most contentious and psychometrically challenging aspects of test development. Numerous methodologies have been proposed to assess item effectiveness for different groups of test takers, and the definitive text in this area is Jensen’s (1980) thoughtful Bias in Mental Testing. Most of the controversy regarding test fairness relates to the lay and legal perception that any group difference in test scores constitutes bias, in and of itself. For example, Jencks and Phillips (1998) stress that the test score gap is the single most important obstacle to achieving racial balance and social equity.
In landmark litigation, Judge Robert Peckham in Larry P. v. Riles (1972/1974/1979/1984/1986) banned the use of individual IQ tests in placing black children into educable mentally retarded classes in California, concluding that the cultural bias of the IQ test was hardly disputed in this litigation. He asserted, “Defendants do not seem to dispute the evidence amassed by plaintiffs to demonstrate that the IQ tests in fact are culturally biased” (Peckham, 1972, p. 1313) and later concluded, “An unbiased test that measures ability or potential should yield the same pattern of scores when administered to different groups of people” (Peckham, 1979, pp. 954–955).
The belief that any group test score difference constitutes bias has been termed the egalitarian fallacy by Jensen (1980, p. 370):
This concept of test bias is based on the gratuitous assumption that all human populations are essentially identical or equal in whatever trait or ability the test purports to measure. Therefore, any difference between populations in the distribution of test scores (such as a difference in means, or standard deviations, or any other parameters of the distribution) is taken as evidence that the test is biased. The search for a less biased test, then, is guided by the criterion of minimizing or eliminating the statistical differences between groups. The perfectly nonbiased test, according to this definition, would reveal reliable individual differences but not reliable (i.e., statistically significant) group differences. (p. 370)
However this controversy is viewed, the perception of test bias stemming from group mean score differences remains a deeply ingrained belief among many psychologists and educators. McArdle (1998) suggests that large group mean score differences are “a necessary but not sufficient condition for test bias” (p. 158). McAllister (1993) has observed, “In the testing community, differences in correct answer rates, total scores, and so on do not mean bias. In the political realm, the exact opposite perception is found; differences mean bias” (p. 394).
The newest models of test fairness describe a systemic approach utilizing both internal and external sources of evidence of fairness that extend from test conception and design through test score interpretation and application (McArdle, 1998; Camilli & Shepard, 1994; Willingham, 1999). These models are important because they acknowledge the importance of the consequences of test use in a holistic assessment of fairness and a multifaceted methodological approach to accumulate evidence of test fairness. In this section, a systemic model of test fairness adapted from the work of several leading authorities is described.
Terms and Definitions
Three key terms appear in the literature associated with test score fairness: bias, fairness, and equity. These concepts overlap but are not identical; for example, a test that shows no evidence of test score bias may be used unfairly. To some extent these terms have historically been defined by families of relevant psychometric analyses—for example, bias is usually associated with differential item functioning, and fairness is associated with differential prediction to an external criterion. In this section, the terms are defined at a conceptual level.
Test score bias tends to be defined in a narrow manner, as a special case of test score invalidity.According to the most recent Standards (1999), bias in testing refers to “construct under-representation or construct-irrelevant components of test scores that differentially affect the performance of different groups of test takers” (p. 172). This definition implies that bias stems from nonrandom measurement error, provided that the typical magnitude of random error is comparable for all groups of interest. Accordingly, test score bias refers to the systematic and invalid introduction of measurement error for a particular group of interest. The statistical underpinnings of this definition have been underscored by Jensen (1980), who asserted, “The assessment of bias is a purely objective, empirical, statistical and quantitative matter entirely independent of subjective value judgments and ethical issues concerning fairness or unfairness of tests and the uses to which they are put” (p. 375). Some scholars consider the characterization of bias as objective and independent of the value judgments associated with fair use of tests to be fundamentally incorrect (e.g., Willingham, 1999).
Test score fairness refers to the ways in which test scores are utilized, most often for various forms of decision-making such as selection. Jensen suggests that test fairness refers “to the ways in which test scores (whether of biased or unbiased tests) are used in any selection situation” (p. 376), arguing that fairness is a subjective policy decision based on philosophic, legal, or practical considerations rather than a statistical decision. Willingham (1999) describes a test fairness manifold that extends throughout the entire process of test development, including the consequences of test usage. Embracing the idea that fairness is akin to demonstrating the generalizability of test validity across population subgroups, he notes that “the manifold of fairness issues is complex because validity is complex” (p. 223). Fairness is a concept that transcends a narrow statistical and psychometric approach.
Finally, equity refers to a social value associated with the intended and unintended consequences and impact of test score usage. Because of the importance of equal opportunity, equal protection, and equal treatment in mental health, education, and the workplace, Willingham (1999) recommends that psychometrics actively consider equity issues in test development. As Tiedeman (1978) noted, “Test equity seems to be emerging as a criterion for test use on a par with the concepts of reliability and validity” (p. xxviii).
Internal Evidence of Fairness
The internal features of a test related to fairness generally include the test’s theoretical underpinnings, item content and format, differential item and test functioning, measurement precision, and factorial structure. The two best-known procedures for evaluating test fairness include expert reviews of content bias and analysis of differential item functioning. These and several additional sources of evidence of test fairness are discussed in this section.
Item Bias and Sensitivity Review
In efforts to enhance fairness, the content and format of psychological and educational tests commonly undergo subjective bias and sensitivity reviews one or more times during test development. In this review, independent representatives from diverse groups closely examine tests, identifying items and procedures that may yield differential responses for one group relative to another. Content may be reviewed for cultural, disability, ethnic, racial, religious, sex, and socioeconomic status bias. For example, a reviewer may be asked a series of questions including, “Does the content, format, or structure of the test item present greater problems for students from some backgrounds than for others?” A comprehensive item bias review is available from Hambleton and Rodgers (1995), and useful guidelines to reduce bias in language are available from the American Psychological Association (1994).
Ideally, there are two objectives in bias and sensitivity reviews: (a) eliminate biased material, and (b) ensure balanced and neutral representation of groups within the test. Among the potentially biased elements of tests that should be avoided are
- material that is controversial, emotionally charged, or inflammatory for any specific group.
- language, artwork, or material that is demeaning or offensive to any specific group.
- content or situations with differential familiarity and relevance for specific groups.
- language and instructions that have different or unfamiliar meanings for specific groups.
- information or skills that may not be expected to be within the educational background of all examinees.
- format or structure of the item that presents differential difficulty for specific groups.
Among the prosocial elements that ideally should be included in tests are
- Presentation of universal experiences in test material.
- Balanced distribution of people from diverse groups.
- Presentation of people in activities that do not reinforce stereotypes.
- Item presentation in a sex-, culture-, age-, and race-neutral manner.
- Inclusion of individuals with disabilities or handicapping conditions.
In general, the content of test materials should be relevant and accessible for the entire population of examinees for whom the test is intended. For example, the experiences of snow and freezing winters are outside the range of knowledge of many Southern students, thereby introducing a geographic regional bias. Use of utensils such as forks may be unfamiliar to Asian immigrants who may instead use chopsticks. Use of coinage from the United States ensures that the test cannot be validly used with examinees from countries with different currency.
Tests should also be free of controversial, emotionally charged, or value-laden content, such as violence or religion. The presence of such material may prove distracting, offensive, or unsettling to examinees from some groups, detracting from test performance.
Stereotyping refers to the portrayal of a group using only a limited number of attributes, characteristics, or roles. As a rule, stereotyping should be avoided in test development. Specific groups should be portrayed accurately and fairly, without reference to stereotypes or traditional roles regarding sex, race, ethnicity, religion, physical ability, or geographic setting. Group members should be portrayed as exhibiting a full range of activities, behaviors, and roles.
Differential Item and Test Functioning
Are item and test statistical properties equivalent for individuals of comparable ability, but from different groups? Differential test and item functioning (DTIF, or DTF and DIF) refers to a family of statistical procedures aimed at determining whether examinees of the same ability but from different groups have different probabilities of success on a test or an item. The most widely used of DIF procedures is the Mantel-Haenszel technique (Holland & Thayer, 1988), which assesses similarities in item functioning across various demographic groups of comparable ability. Items showing significant DIF are usually considered for deletion from a test.
DIF has been extended by Shealy and Stout (1993) to a test score–based level of analysis known as differential test functioning, a multidimensional nonparametric IRT index of test bias. Whereas DIF is expressed at the item level, DTF represents a combination of two or more items to produce DTF, with scores on a valid subtest used to match examinees according to ability level. Tests may show evidence of DIF on some items without evidence of DTF, provided item bias statistics are offsetting and eliminate differential bias at the test score level.
Although psychometricians have embraced DIF as a preferred method for detecting potential item bias (McAllister, 1993), this methodology has been subjected to increasing criticism because of its dependence upon internal test properties and its inherent circular reasoning. Hills (1999) notes that two decades of DIF research have failed to demonstrate that removing biased items affects test bias and narrows the gap in group mean scores. Furthermore, DIF rests on several assumptions, including the assumptions that items are unidimensional, that the latent trait is equivalently distributed across groups, that the groups being compared (usually racial, sex, or ethnic groups) are homogeneous, and that the overall test is unbiased. Camilli and Shepard (1994) observe, “By definition, internal DIF methods are incapable of detecting constant bias. Their aim, and capability, is only to detect relative discrepancies” (p. 17).
Additional Internal Indexes of Fairness
The demonstration that a test has equal internal integrity across racial and ethnic groups has been described as a way to demonstrate test fairness (e.g., Mercer, 1984). Among the internal psychometric characteristics that may be examined for this type of generalizability are internal consistency, item difficulty calibration, test-retest stability, and factor structure.
With indexes of internal consistency, it is usually sufficient to demonstrate that the test meets the guidelines such as those recommended above for each of the groups of interest, consideredindependently(Jensen,1980).Demonstrationofadequate measurement precision across groups suggests that a test has adequate accuracy for the populations in which it may be used. Geisinger (1998) noted that “subgroup-specific reliability analysis may be especially appropriate when the reliability of a test has been justified on the basis of internal consistency reliability procedures (e.g., coefficient alpha). Such analysis should be repeated in the group of special test takers because the meaning and difficulty of some components of the test may change over groups, especially over some cultural, linguistic, and disability groups” (p. 25). Differences in group reliabilities may be evident, however, when test items are substantially more difficult for one group than another or when ceiling or floor effects are present for only one group.
ARasch-based methodology to compare relative difficulty of test items involves separate calibration of items of the test for each group of interest (e.g., O’Brien, 1992). The items may then be plotted against an identity line in a bivariate graph and bounded by 95 percent confidence bands. Items falling within the bands are considered to have invariant difficulty, whereas items falling outside the bands have different difficulty and may have different meanings across the two samples.
The temporal stability of test scores should also be compared across groups, using similar test-retest intervals, in order to ensure that test results are equally stable irrespective of race and ethnicity. Jensen (1980) suggests,
If a test is unbiased, test-retest correlation, of course with the same interval between testings for the major and minor groups, should yield the same correlation for both groups. Significantly different test-retest correlations (taking proper account of possibly unequal variances in the two groups) are indicative of a biased test. Failure to understand instructions, guessing, carelessness, marking answers haphazardly, and the like, all tend to lower the test-retest correlation. If two groups differ in test-retest correlation, it is clear that the test scores are not equally accurate or stable measures of both groups. (p. 430)
As an index of construct validity, the underlying factor structure of psychological tests should be robust across racial and ethnic groups. A difference in the factor structure across groups provides some evidence for bias even though factorial invariance does not necessarily signify fairness (e.g., Meredith, 1993; Nunnally & Bernstein, 1994). Floyd and Widaman (1995) suggested, “Increasing recognition of cultural, developmental, and contextual influences on psychological constructs has raised interest in demonstrating measurement invariance before assuming that measures are equivalent across groups” (p. 296).
External Evidence of Fairness
Beyond the concept of internal integrity, Mercer (1984) recommended that studies of test fairness include evidence of equal external relevance. In brief, this determination requires the examination of relations between item or test scores and independent external criteria. External evidence of test score fairness has been accumulated in the study of comparative prediction of future performance (e.g., use of the Scholastic Assessment Test across racial groups to predict a student’s ability to do college-level work). Fair prediction and fair selection are two objectives that are particularly important as evidence of test fairness, in part because they figure prominently in legislation and court rulings.
Fair Prediction
Prediction bias can arise when a test differentially predicts future behaviors or performance across groups. Cleary (1968) introduced a methodology that evaluates comparative predictive validity between two or more salient groups. The Cleary rule states that a test may be considered fair if it has the same approximate regression equation, that is, comparable slope and intercept, explaining the relationship between the predictor test and an external criterion measure in the groups undergoing comparison.Aslope difference between the two groups conveys differential validity and relates that one group’s performance on the external criterion is predicted less well than the other’s performance. An intercept difference suggests a difference in the level of estimated performance between the groups, even if the predictive validity is comparable. It is important to note that this methodology assumes adequate levels of reliability for both the predictor and criterion variables. This procedure has several limitations that have been summarized by Camilli and Shepard (1994). The demonstration of equivalent predictive validity across demographic groups constitutes an important source of fairness that is related to validity generalization.
Fair Selection
The consequences of test score use for selection and decisionmaking in clinical, educational, and occupational domains constitute a source of potential bias. The issue of fair selection addresses the question of whether the use of test scores for selection decisions unfairly favors one group over another. Specifically, test scores that produce adverse, disparate, or disproportionate impact for various racial or ethnic groups may be said to show evidence of selection bias, even when that impact is construct relevant. Since enactment of the Civil Rights Act of 1964, demonstration of adverse impact has been treated in legal settings as prima facie evidence of test bias.Adverse impact occurs when there is a substantially different rate of selection based on test scores and other factors that works to the disadvantage of members of a race, sex, or ethnic group.
Federal mandates and court rulings have frequently indicated that adverse, disparate, or disproportionate impact in selection decisions based upon test scores constitutes evidence of unlawful discrimination, and differential test selection rates among majority and minority groups have been considered a bottom line in federal mandates and court rulings. In its Uniform Guidelines on Employment Selection Procedures (1978), the Equal Employment Opportunity Commission (EEOC) operationalized adverse impact according to the four-fifths rule, which states, “A selection rate for any race, sex, or ethnic group which is less than four-fifths (4/5) (or eighty percent) of the rate for the group with the highest rate will generally be regarded by the Federal enforcement agencies as evidence of adverse impact” (p. 126). Adverse impact has been applied to educational tests (e.g., the Texas Assessment of Academic Skills) as well as tests used in personnel selection. The U.S. Supreme Court held in 1988 that differential selection ratios can constitute sufficient evidence of adverse impact. The 1991 Civil Rights Act, Section 9, specifically and explicitly prohibits any discriminatory use of test scores for minority groups.
Since selection decisions involve the use of test cutoff scores, an analysis of costs and benefits according to decision theory provides a methodology for fully understanding the consequences of test score usage. Cutoff scores may be varied to provide optimal fairness across groups, or alternative cutoff scores may be utilized in certain circumstances. McArdle (1998) observes, “As the cutoff scores become increasingly stringent, the number of false negative mistakes (or costs) also increase, but the number of false positive mistakes (also a cost) decrease” (p. 174).
The Limits of Psychometrics
Psychological assessment is ultimately about the examinee.A test is merely a tool with which to understand the examinee, and psychometrics are merely rules with which to build the tools. The tools themselves must be sufficiently sound (i.e., valid and reliable) and fair that they introduce acceptable levels of error into the process of decision-making. Some guidelines have been described above for psychometrics of test construction and application that help us not only to build better tools, but to use these tools as skilled craftspersons.
As an evolving field of study, psychometrics still has some glaring shortcomings. A long-standing limitation of psychometrics is its systematic overreliance on internal sources of evidence for test validity and fairness. In brief, it is more expensive and more difficult to collect external criterion-based information, especially with special populations; it is simpler and easier to base all analyses on the performance of a normative standardization sample. This dependency on internal methods has been recognized and acknowledged by leading psychometricians. In discussing psychometric methods for detecting test bias, for example, Camilli and Shepard cautioned about circular reasoning: “Because DIF indices rely only on internal criteria, they are inherently circular” (p. 17). Similarly, there has been reticence among psychometricians in considering attempts to extend the domain of validity into consequential aspects of test usage (e.g., Lees-Haley, 1996). We have witnessed entire testing approaches based upon internal factor-analytic approaches and evaluation of content validity (e.g., McGrew & Flanagan, 1998), with negligible attention paid to the external validation of the factors against independent criteria. This shortcoming constitutes a serious limitation of psychometrics, which we have attempted to address by encouraging the use of both internal and external sources of psychometric evidence.
Another long-standing limitation is the tendency of test developers to wait until the test is undergoing standardization to establish its validity. A typical sequence of test development involves pilot studies, a content tryout, and finally a national standardization and supplementary studies (e.g., Robertson, 1992). Harkening back to the stages described by Loevinger (1957), the external criterion-based validation stage comes last in the process—after the test has effectively been built. It constitutes a limitation in psychometric practice that many tests only validate their effectiveness for a stated purpose at the end of the process, rather than at the beginning, as MMPI developers did over half a century ago by selecting items that discriminated between specific diagnostic groups (Hathaway & McKinley, 1943). The utility of a test for its intended application should be partially validated at the pilot study stage, prior to norming.
Finally, psychometrics has failed to directly address many of the applied questions of practitioners. Tests results often do not readily lend themselves to functional decisionmaking. For example, psychometricians have been slow to develop consensually accepted ways of measuring growth and maturation, reliable change (as a result of enrichment, intervention, or treatment), and atypical response patterns suggestive of lack of effort or dissimilation. The failure of treatment validity and assessment-treatment linkage undermines the central purpose of testing. Moreover, recent challenges to the practice of test profile analysis (e.g., Glutting, McDermott, & Konold, 1997) suggest a need to systematically measure test profile strengths and weaknesses in a clinically relevant way that permits a match to prototypal expectations for specific clinical disorders. The answers to these challenges lie ahead.
Bibliography:
- Achenbach, T. M., & Howell, C. T. (1993). Are American children’s problems getting worse? A 13-year comparison. Journal of the American Academy of Child and Adolescent Psychiatry, 32, 1145–1154.
- American Educational Research Association. (1999). Standards for educational and psychological testing. Washington, DC: Author.
- American Psychological Association. (1992). Ethical principles of psychologists and code of conduct. American Psychologist, 47, 1597–1611.
- American PsychologicalAssociation. (1994). Publication manual of the American Psychological Association (4th ed.). Washington, DC: Author.
- Anastasi, A., & Urbina, S. (1997). Psychological testing (7th ed.). Upper Saddle River, NJ: Prentice Hall.
- Andrich,D.(1988).ThousandOaks, CA: Sage.
- Angoff,W.H.(1984).Scales,norms,andequivalentscores.Princeton, NJ: EducationalTesting Service.
- Banaji, M. R., & Crowder, R. C. (1989). The bankruptcy of everyday memory. American Psychologist, 44, 1185–1193.
- Barrios, B. A. (1988). On the changing nature of behavioral assessment. In A. S. Bellack & M. Hersen (Eds.), Behavioral assessment: A practical handbook (3rd ed., pp. 3–41). New York: Pergamon Press.
- Bayley, N. (1993). Bayley Scales of Infant Development second editionmanual.SanAntonio,TX:ThePsychologicalCorporation.
- Beutler, L. E. (1998). Identifying empirically supported treatments: What if we didn’t? Journal of Consulting and Clinical Psychology, 66, 113–120.
- Beutler, L. E., & Clarkin, J. F. (1990). Systematic treatment selection: Toward targeted therapeutic interventions. Philadelphia, PA: Brunner/Mazel.
- Beutler, L. E., & Harwood, T. M. (2000). Prescriptive psychotherapy: A practical guide to systematic treatment selection. New York: Oxford University Press.
- Binet, A., & Simon, T. (1916). New investigation upon the measure of the intellectual level among school children. In E. S. Kite (Trans.), The development of intelligence in children (pp. 274– 329). Baltimore:Williams andWilkins. (Original work published 1911).
- Bracken, B. A. (1987). Limitations of preschool instruments and standards for minimal levels of technical adequacy. Journal of Psychoeducational Assessment, 4, 313–326.
- Bracken, B. A. (1988). Ten psychometric reasons why similar tests produce dissimilar results. Journal of School Psychology, 26, 155–166.
- Bracken, B. A., & McCallum, R. S. (1998). Universal Nonverbal Intelligence Test examiner’s manual. Itasca, IL: Riverside.
- Brown, W. (1910). Some experimental results in the correlation of mental abilities. British Journal of Psychology, 3, 296–322.
- Bruininks, R. H., Woodcock, R. W., Weatherman, R. F., & Hill, B. K. (1996). Scales of Independent Behavior—Revised comprehensive manual. Itasca, IL: Riverside.
- Butcher, J. N., Dahlstrom, W. G., Graham, J. R., Tellegen, A., & Kaemmer, B. (1989). Minnesota Multiphasic Personality Inventory-2 (MMPI-2): Manual for administration and scoring. Minneapolis: University of Minnesota Press.
- Camilli, G., & Shepard, L. A. (1994). Methods for identifying biased test items (Vol. 4). Thousand Oaks, CA: Sage.
- Campbell, D. T., & Fiske, D. W. (1959). Convergent and discriminant validation by the multitrait-multimethod matrix. Psychological Bulletin, 56, 81–105.
- Campbell, D. T., & Stanley, J. C. (1963). Experimental and quasiexperimental designs for research. Chicago: Rand-McNally.
- Campbell, S. K., Siegel, E., Parr, C. A., & Ramey, C. T. (1986). Evidence for the need to renorm the Bayley Scales of Infant Development based on the performance of a population-based sample of 12-month-old infants. Topics in Early Childhood Special Education, 6, 83–96.
- Carroll, J. B. (1983). Studying individual differences in cognitive abilities: Through and beyond factor analysis. In R. F. Dillon & R. R. Schmeck (Eds.), Individual differences in cognition (pp. 1–33). New York: Academic Press.
- Cattell, R. B. (1986). The psychometric properties of tests: Consistency, validity, and efficiency. In R. B. Cattell & R. C. Johnson (Eds.), Functional psychological testing: Principles and instruments (pp. 54–78). New York: Brunner/Mazel.
- Chudowsky, N., & Behuniak, P. (1998). Using focus groups to examine the consequential aspect of validity. Educational Measurement: Issues and Practice, 17, 28–38.
- Cicchetti, D. V. (1994). Guidelines, criteria, and rules of thumb for evaluating normed and standardized assessment instruments in psychology. Psychological Assessment, 6, 284–290.
- Clark, L. A., & Watson, D. (1995). Constructing validity: Basic issues in objective scale development. Psychological Assessment, 7, 309–319.
- Cleary, T. A. (1968). Test bias: Prediction of grades for Negro and White students in integrated colleges. Journal of Educational Measurement, 5, 115–124.
- Cone,J.D.(1978).Thebehavioralassessmentgrid(BAG):Aconceptual framework and a taxonomy. Behavior Therapy, 9, 882–888.
- Cone, J. D. (1988). Psychometric considerations and the multiple models of behavioral assessment. In A. S. Bellack & M. Hersen (Eds.), Behavioral assessment: A practical handbook (3rd ed., pp. 42–66). New York: Pergamon Press.
- Cook, T. D., & Campbell, D. T. (1979). Quasi-experimentation: Design and analysis issues for field settings. Chicago: RandMcNally.
- Crocker, L., & Algina, J. (1986). Introduction to classical and modern test theory. New York: Holt, Rinehart, and Winston.
- Cronbach, L. J. (1957). The two disciplines of scientific psychology. American Psychologist, 12, 671–684.
- Cronbach, L. J. (1971). Test validation. In R. L. Thorndike (Ed.), Educational measurement (2nd ed., pp. 443–507). Washington, DC: American Council on Education.
- Cronbach, L. J., & Gleser, G. C. (1965). Psychological tests and personnel decisions. Urbana: University of Illinois Press.
- Cronbach, L. J., Gleser, G. C., Nanda, H., & Rajaratnam, N. (1972). The dependability of behavioral measurements: Theory of generalizability scores and profiles. New York: Wiley.
- Cronbach, L. J., & Meehl, P. E. (1955). Construct validity in psychological tests. Psychological Bulletin, 52, 281–302.
- Cronbach, L. J., Rajaratnam, N., & Gleser, G. C. (1963). Theory of generalizability: A liberalization of reliability theory. British Journal of Statistical Psychology, 16, 137–163.
- Daniel, M. H. (1999). Behind the scenes: Using new measurement methods on the DAS and KAIT. In S. E. Embretson & S. L. Hershberger (Eds.), The new rules of measurement: What every psychologist and educator should know (pp. 37–63). Mahwah, NJ: Erlbaum.
- Elliott, C. D. (1990). Differential Ability Scales: Introductory and technical handbook. San Antonio, TX: The Psychological Corporation.
- Embretson, S. E. (1995). The new rules of measurement. Psychological Assessment, 8, 341–349.
- Embretson, S. E. (1999). Issues in the measurement of cognitive abilities. In S. E. Embretson & S. L. Hershberger (Eds.), The new rules of measurement: What every psychologist and educator should know (pp. 1–15). Mahwah, NJ: Erlbaum.
- Embretson, S. E., & Hershberger, S. L. (Eds.). (1999). The new rules of measurement: What every psychologist and educator should know. Mahwah, NJ: Erlbaum.
- Fiske, D. W., & Campbell, D. T. (1992). Citations do not solve problems. Psychological Bulletin, 112, 393–395.
- Fleiss, J. L. (1981). Balanced incomplete block designs for interrater reliability studies. Applied Psychological Measurement, 5, 105–112.
- Floyd, F. J., & Widaman, K. F. (1995). Factor analysis in the development and refinement of clinical assessment instruments. Psychological Assessment, 7, 286–299.
- Flynn, J. R. (1984). The mean IQ of Americans: Massive gains 1932 to 1978. Psychological Bulletin, 95, 29–51.
- Flynn, J. R. (1987). Massive IQ gains in 14 nations: What IQ tests really measure. Psychological Bulletin, 101, 171–191.
- Flynn, J. R. (1994). IQ gains over time. In R. J. Sternberg (Ed.), The encyclopedia of human intelligence (pp. 617–623). New York: Macmillan.
- Flynn, J. R. (1999). Searching for justice: The discovery of IQ gains over time. American Psychologist, 54, 5–20.
- Galton, F. (1879). Psychometric experiments. Brain: A Journal of Neurology, 2, 149–162.
- Geisinger, K. F. (1992). The metamorphosis of test validation. Educational Psychologist, 27, 197–222.
- Geisinger, K. F. (1998). Psychometric issues in test interpretation. In Sandoval, C. L. Frisby, K. F. Geisinger, J. D. Scheuneman, & J. R. Grenier (Eds.), Test interpretation and diversity: Achieving equity in assessment (pp. 17–30). Washington, DC: American Psychological Association.
- Gleser, G. C., Cronbach, L. J., & Rajaratnam, N. (1965). Generalizability of scores influenced by multiple sources of variance. Psychometrika, 30, 395–418.
- Glutting, J. J., McDermott, P. A., & Konold, T. R. (1997). Ontology, structure, and diagnostic benefits of a normative subtest taxonomy from the WISC-III standardization sample. In D. P. Flanagan, J. L. Genshaft, & P. L. Harrison (Eds.), Contemporary intellectual assessment: Theories, tests, and issues (pp. 349– 372). New York: Guilford Press.
- Gorsuch, R. L. (1983). Factor analysis (2nd ed.). Hillsdale, NJ: Erlbaum.
- Guilford, J. P. (1950). Fundamental statistics in psychology and education (2nd ed.). New York: McGraw-Hill.
- Guion, R. M. (1977). Content validity: The source of my discontent. Applied Psychological Measurement, 1, 1–10.
- Gulliksen, H. (1950). Theory of mental tests. New York: McGrawHill.
- Hambleton, R. K., & Rodgers, J. H. (1995). Item bias review. Washington, DC: The Catholic University of America, Department of Education. (ERIC Clearinghouse on Assessment and Evaluation, No. EDO-TM-95–9)
- Hambleton, R. K., Swaminathan, H., & Rogers, H. J. (1991). Fundamentals of item response theory. Newbury Park, CA: Sage.
- Hathaway, S. R., & McKinley, J. C. (1943). Manual for the Minnesota Multiphasic Personality Inventory. New York: The Psychological Corporation.
- Hayes, S. C., Nelson, R. O., & Jarrett, R. B. (1987). The treatment utility of assessment: Afunctional approach to evaluating assessment quality. American Psychologist, 42, 963–974.
- Haynes, S. N., Richard, D. C. S., & Kubany, E. S. (1995). Content validity in psychological assessment: A functional approach to concepts and methods. Psychological Assessment, 7, 238–247.
- Heinrichs, R. W. (1990). Current and emergent applications of neuropsychological assessment problems of validity and utility. Professional Psychology: Research and Practice, 21, 171–176.
- Herrnstein, R. J., & Murray, C. (1994). The bell curve: Intelligence and class in American life. New York: Free Press.
- Hills, J. (1999, May 14). Re: Construct validity. Educational Statistics Discussion List (EDSTAT-L). (Available from edstat-l @jse.stat.ncsu.edu)
- Holland, P. W., & Thayer, D. T. (1988). Differential item functioning and the Mantel-Haenszel procedure. In H. Wainer & H. I. Braun (Eds.), Test validity (pp. 129–145). Hillsdale, NJ: Erlbaum.
- Hopkins, C. D., & Antes, R. L. (1978). Classroom measurement and evaluation. Itasca, IL: F. E. Peacock.
- Hunter, J. E., & Schmidt, F. L. (1990). Methods of meta-analysis: Correcting error and bias in research findings. Newbury Park, CA: Sage.
- Hunter, J. E., Schmidt, F. L., & Jackson, C. B. (1982). Advanced meta-analysis: Quantitative methods of cumulating research findings across studies. San Francisco: Sage.
- Ittenbach, R. F., Esters, I. G., &Wainer, H. (1997).The history of test development. In D. P. Flanagan, J. L. Genshaft, & P. L. Harrison (Eds.), Contemporary intellectual assessment: Theories, tests, and issues (pp. 17–31). New York: Guilford Press.
- Jackson, D. N. (1971). A sequential system for personality scale development. In C. D. Spielberger (Ed.), Current topics in clinical and community psychology (Vol. 2, pp. 61–92). New York: Academic Press.
- Jencks, C., & Phillips, M. (Eds.). (1998). The Black-White test score gap. Washington, DC: Brookings Institute.
- Jensen, A. R. (1980). Bias in mental testing. New York: Free Press.
- Johnson, N. L. (1949). Systems of frequency curves generated by methods of translation. Biometika, 36, 149–176.
- Kalton, G. (1983). Introduction to survey sampling. Beverly Hills, CA: Sage.
- Kaufman,A. S., & Kaufman, N. L. (1983). KaufmanAssessment Battery for Children. Circle Pines, MN:American Guidance Service.
- Keith, T. Z., & Kranzler, J. H. (1999). The absence of structural fidelity precludes construct validity: Rejoinder to Naglieri on what the Cognitive Assessment System does and does not measure. School Psychology Review, 28, 303–321.
- Knowles, E. S., & Condon, C. A. (2000). Does the rose still smell as sweet? Item variability across test forms and revisions. Psychological Assessment, 12, 245–252.
- Kolen, M. J., Zeng, L., & Hanson, B. A. (1996). Conditional standard errors of measurement for scale scores using IRT. Journal of Educational Measurement, 33, 129–140.
- Kuhn, T. (1970). The structure of scientific revolutions (2nd ed.). Chicago: University of Chicago Press.
- Larry P. v. Riles, 343 F. Supp. 1306 (N.D. Cal. 1972) (order granting injunction), aff’d 502 F.2d 963 (9th Cir. 1974); 495 F. Supp. 926 (N.D. Cal. 1979) (decision on merits), aff’d (9th Cir. No. 80-427 Jan. 23, 1984). Order modifying judgment, C-71-2270 RFP, September 25, 1986.
- Lazarus, A. A. (1973). Multimodal behavior therapy: Treating the BASIC ID. Journal of Nervous and Mental Disease, 156, 404– 411.
- Lees-Haley, P. R. (1996). Alice in validityland, or the dangerous consequences of consequential validity. American Psychologist, 51, 981–983.
- Levy, P. S., & Lemeshow, S. (1999). Sampling of populations: Methods and applications. New York: Wiley.
- Li, H., Rosenthal, R., & Rubin, D. B. (1996). Reliability of measurement in psychology: From Spearman-Brown to maximal reliability. Psychological Methods, 1, 98–107.
- Li, H., & Wainer, H. (1997). Toward a coherent view of reliability in test theory. Journal of Educational and Behavioral Statistics, 22, 478–484.
- Linacre, J. M., & Wright, B. D. (1999). A user’s guide to Winsteps/ Ministep: Rasch-model computer programs. Chicago: MESA Press.
- Linn, R. L. (1998). Partitioning responsibility for the evaluation of the consequences of assessment programs. Educational Measurement: Issues and Practice, 17, 28–30.
- Loevinger, J. (1957). Objective tests as instruments of psychological theory [Monograph]. Psychological Reports, 3, 635–694.
- Loevinger, J. (1972). Some limitations of objective personality tests. In J. N. Butcher (Ed.), Objective personality assessment (pp. 45– 58). New York: Academic Press.
- Lord, F. N., & Novick, M. (1968). Statistical theories of mental tests. New York: Addison-Wesley.
- Maruish, M. E. (Ed.). (1999). The use of psychological testing for treatment planning and outcomes assessment. Mahwah, NJ: Erlbaum.
- McAllister, P. H. (1993). Testing, DIF, and public policy. In P. W. Holland & H. Wainer (Eds.), Differential item functioning (pp. 389–396). Hillsdale, NJ: Erlbaum.
- McArdle, J. J. (1998). Contemporary statistical models for examining test-bias. In J. J. McArdle & R. W. Woodcock (Eds.), Human cognitiveabilitiesintheoryandpractice(pp.157–195).Mahwah, NJ: Erlbaum.
- McGrew, K. S., & Flanagan, D. P. (1998). The intelligence test desk reference (ITDR): Gf-Gc cross-battery assessment. Boston: Allyn and Bacon.
- McGrew, K. S., & Woodcock, R. W. (2001). Woodcock-Johnson III technical manual. Itasca, IL: Riverside.
- Meehl, P. E. (1972). Reactions, reflections, projections. In J. N. Butcher (Ed.), Objective personality assessment: Changing perspectives (pp. 131–189). New York: Academic Press.
- Mercer, J. R. (1984). What is a racially and culturally nondiscriminatory test? A sociological and pluralistic perspective. In C. R. Reynolds & R. T. Brown (Eds.), Perspectives on bias in mental testing (pp. 293–356). New York: Plenum Press.
- Meredith, W. (1993). Measurement invariance, factor analysis and factorial invariance. Psychometrika, 58, 525–543.
- Messick, S. (1989). Meaning and values in test validation: The science and ethics of assessment. Educational Researcher, 18, 5–11.
- Messick, S. (1995a). Standards of validity and the validity of standards in performance assessment. Educational Measurement: Issues and Practice, 14, 5–8.
- Messick, S. (1995b). Validity of psychological assessment: Validation of inferences from persons’ responses and performances as scientific inquiry into score meaning. American Psychologist, 50, 741–749.
- Millon, T., Davis, R., & Millon, C. (1997). MCMI-III: Millon Clinical Multiaxial Inventory-III manual (3rd ed.). Minneapolis, MN: National Computer Systems.
- Naglieri, J. A., & Das, J. P. (1997). Das-Naglieri Cognitive Assessment System interpretive handbook. Itasca, IL: Riverside.
- Neisser, U. (1978). Memory: What are the important questions? In M. M. Gruneberg, P. E. Morris, & R. N. Sykes (Eds.), Practical aspects of memory (pp. 3–24). London: Academic Press.
- Newborg, J., Stock, J. R., Wnek, L., Guidubaldi, J., & Svinicki, J. (1984). Battelle Developmental Inventory. Itasca, IL: Riverside.
- Newman, J. R. (1956). The world of mathematics: A small library of literature of mathematics from A’h-mose the Scribe to Albert Einstein presented with commentaries and notes. New York: Simon and Schuster.
- Nunnally, J. C., & Bernstein, I. H. (1994). Psychometric theory (3rd ed.). New York: McGraw-Hill.
- O’Brien, M. L. (1992). ARasch approach to scaling issues in testing Hispanics. In K. F. Geisinger (Ed.), Psychological testing of Hispanics (pp. 43–54). Washington, DC: American Psychological Association.
- Peckham, R. F. (1972). Opinion, Larry P. v. Riles. Federal Supplement, 343, 1306–1315.
- Peckham, R. F. (1979). Opinion, Larry P. v. Riles. Federal Supplement, 495, 926–992.
- Pomplun, M. (1997). State assessment and instructional change: A path model analysis. Applied Measurement in Education, 10, 217–234.
- Rasch, G. (1960). Probabilistic models for some intelligence and attainment tests. Copenhagen: Danish Institute for Educational Research.
- Reckase, M. D. (1998). Consequential validity from the test developer’s perspective. Educational Measurement: Issues and Practice, 17, 13–16.
- Reschly, D. J. (1997). Utility of individual ability measures and public policy choices for the 21st century. School Psychology Review, 26, 234–241.
- Riese, S. P., Waller, N. G., & Comrey, A. L. (2000). Factor analysis and scale revision. Psychological Assessment, 12, 287–297.
- Robertson, G. J. (1992). Psychological tests: Development, publication, and distribution. In M. Zeidner & R. Most (Eds.), Psychological testing: An inside view (pp. 159–214). Palo Alto, CA: Consulting Psychologists Press.
- Salvia, J., & Ysseldyke, J. E. (2001). Assessment (8th ed.). Boston: Houghton Mifflin.
- Samejima, F. (1994). Estimation of reliability coefficients using the test information function and its modifications. Applied Psychological Measurement, 18, 229–244.
- Schmidt, F. L., & Hunter, J. E. (1977). Development of a general solution to the problem of validity generalization. Journal of Applied Psychology, 62, 529–540.
- Shealy, R., & Stout, W. F. (1993). A model-based standardization approach that separates true bias/DIF from group differences and detects test bias/DTF as well as item bias/DIF. Psychometrika, 58, 159–194.
- Shrout, P. E., & Fleiss, J. L. (1979). Intraclass correlations: Uses in assessing rater reliability. Psychological Bulletin, 86, 420–428.
- Spearman,C.(1910).Correlation calculatedfrom faulty data.British Journal of Psychology, 3, 171–195.
- Stinnett, T. A., Coombs, W. T., Oehler-Stinnett, J., Fuqua, D. R., & Palmer, L. S. (1999, August). NEPSY structure: Straw, stick, or brick house? Paper presented at the Annual Convention of the American Psychological Association, Boston, MA.
- Suen, H. K. (1990). Principles of test theories. Hillsdale, NJ: Erlbaum.
- Swets, J. A. (1992). The science of choosing the right decision threshold in high-stakes diagnostics. American Psychologist, 47, 522–532.
- Terman, L. M. (1916). The measurement of intelligence: An explanation of and a complete guide for the use of the Stanford revision and extension of the Binet Simon Intelligence Scale. Boston: Houghton Mifflin.
- Terman, L. M., & Merrill, M. A. (1937). Directions for administering: Forms L and M, Revision of the Stanford-Binet Tests of Intelligence. Boston: Houghton Mifflin.
- Tiedeman, D. V. (1978). In O. K. Buros (Ed.), The eight mental measurements yearbook. Highland Park: NJ: Gryphon Press.
- Tinsley, H. E. A., & Weiss, D. J. (1975). Interrater reliability and agreement of subjective judgments. Journal of Counseling Psychology, 22, 358–376.
- Tulsky, D. S., & Ledbetter, M. F. (2000). Updating to the WAIS-III and WMS-III: Considerations for research and clinical practice. Psychological Assessment, 12, 253–262.
- Uniform guidelines on employee selection procedures. (1978). Federal Register, 43, 38296–38309.
- Vacha-Haase, T. (1998). Reliability generalization: Exploring variance in measurement error affecting score reliability across studies. Educational and Psychological Measurement, 58, 6–20.
- Walker, K. C., & Bracken, B. A. (1996). Inter-parent agreement on four preschool behavior rating scales: Effects of parent and child gender. Psychology in the Schools, 33, 273–281.
- Wechsler, D. (1939). The measurement of adult intelligence. Baltimore: Williams and Wilkins.
- Wechsler, D. (1946). The Wechsler-Bellevue Intelligence Scale: Form II. Manual for administering and scoring the test. New York: The Psychological Corporation.
- Wechsler, D. (1949). Wechsler Intelligence Scale for Children manual. New York: The Psychological Corporation.
- Wechsler, D. (1974). Manual for the Wechsler Intelligence Scale for Children–Revised. New York: The Psychological Corporation.
- Wechsler, D. (1991). Wechsler Intelligence Scale for Children (3rd ed.). San Antonio, TX: The Psychological Corporation.
- Willingham, W. W. (1999). A systematic view of test fairness. In S. J. Messick (Ed.), Assessment in higher education: Issues of access, quality, student development, and public policy (pp. 213– 242). Mahwah, NJ: Erlbaum.
- Wood, J. M., Nezworski, M. T., & Stejskal, W. J. (1996). The comprehensive system for the Rorschach: A critical examination. Psychological Science, 7, 3–10.
- Woodcock, R. W. (1999). What can Rasch-based scores convey about a person’s test performance? In S. E. Embretson & S. L. Hershberger (Eds.), The new rules of measurement: What every psychologist and educator should know (pp. 105–127). Mahwah, NJ: Erlbaum.
- Wright, B. D. (1999). Fundamental measurement for psychology. In S. E. Embretson & S. L. Hershberger (Eds.), The new rules of measurement: What every psychologist and educator should know (pp. 65–104). Mahwah, NJ: Erlbaum.
- Zieky, M. (1993). Practical questions in the use of DIF statistics in test development. In P. W. Holland & H. Wainer (Eds.), Differential item functioning (pp. 337–347). Hillsdale, NJ: Erlbaum.




