Formal Theory Of Population Cycles Research Paper

1. Mechanisms Driving Population Cycles

To explain the different mechanisms that drive cycles, and the kinds of formal theory that are required, it is useful to begin with Lotka’s classical demographic equation which relates births B(t) at the present time t > 0 to past births, by summing the reproductive contributions φ(a, t) made by individuals of all ages a, as

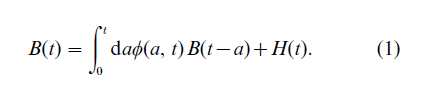
Here H(t) specifies births to individuals who were present at t = 0, and immigration is ignored. The theory of this classical demographic model is discussed in Population Dynamics: Theory of Stable Populations; Population Dynamics: Classical Applications of Stable Population Theory; Population Dynamics: Theory of Nonstable Populations.

Transient cycles typically occur in a population whose vital rates, i.e., mortality and fertility, change over a time interval, say from t = 0 to t = t₁, and are constant thereafter. A practical example of such a perturbation is a decline from high fertility to replacement fertility that starts at t = 0 and is completed at t = t₁. After time t₁, the population is described by classical demographic theory and undergoes damped oscillations towards the classical stationary state. But the dynamics during the transition are also oscillatory and require a different treatment.

Externally driven cycles result from a persistent perturbation of vital rates. One example is a periodic variation over time in fertility that is generated by an exogenous force, such as an economic cycle in wages. Another example is an irregular, stochastic variation in fertility or mortality that produces an ongoing stochastic response that has cyclical components. Formally, such perturbations are described by an appropriate time-dependence in the function φ(a, t).

Internally driven cycles result from changes in vital rates that are driven by changes in population size and composition. In such cases, the net reproduction φ(a, t) has a functional dependence on the past trajectory of births, or on past vital rates. One example is a relationship between the fertility of a cohort in its childbearing years with the size of the cohort: for a substantive discussion of such relationships, see Fertility Transition: Economic Explanations; Baby Booms and Baby Busts in the Twentieth Century; Population Cycles and Demographic Behavior. Another example is provided by inverse projection in historical demography (Lee 1977), in which observed counts of births and deaths over time are used in conjunction with the Lotka equation to estimate the time-variation in the level of mortality rates. Here, the constraint of matching observed counts results in a feedback between the level of mortality and population counts (Wachter 1986).

The formal theory of cycles driven by each of these mechanisms is discussed below, followed by a brief consideration of future directions.

2. Transient Cycles

A perturbation such as a fertility transition may take decades to complete, and a formal theory must provide formulas for the birth sequence B(t) both during and after the perturbation. Li and Tuljapurkar (1999b) provide an explicit if cumbersome description of the decaying population cycles that result from a perturbation. This theory shows that the population undergoes damped cyclical changes during and after the transition. The characteristics of these cycles have not been explored except in particular cases; but this analysis makes possible the computation of population momentum for all gradual transitions (Li and Tuljapurkar 1999a). It is worth noting that the analytical results for this case rest on properties of the roots of Lotka’s equation. The relationship between these roots and the age-pattern of reproduction has been studied by approximate (Keyfitz 1985) and exact (Wachter 1984) methods that are also useful in the analysis of externally and internally driven cycles.

3. Externally Driven Cycles

An illuminating treatment of population cycles driven by external periodic variation in reproduction was given by Coale (1972), who showed that the population responds with periodic variation in the numbers and relative sizes of its age components. The challenge for the theory lies in the nonlinearity of eqn. (1) when φ(a, t) contains a periodic component. To see this, suppose that φ(a, t) = φ(a) + ψ(a, t) with ψ being periodic in time t, and suppose that the resulting birth sequence in eqn. (1) has the form B(t) = B + b(t), with b also a periodic function. Substitution of these forms into eqn. (1) shows that the unknown b(t) depends on a nonlinear product ψ(a, t -a) b(t – a). General results for nonlinear renewal eqns. of this type are not known. There are analytical approximations which employ an expansion in the amplitude of the periodic perturbation ψ; these describe the amplitude response of the population and the phase difference between population cycles and the external driving cycle (Tuljapurkar 1985). An interesting class of periodically perturbed Lotka models has been described and analyzed exactly by Kim and Schoen (1997), Schoen and Kim (1994, 1997). The latter work demonstrates that it is sometimes possible to solve exactly the homogeneous form of equation (1), i.e., with H = 0, for an explicitly time-dependent φ(a, t). Such analytical examples can be valuable as a source of insight into the dynamics, and as a check on approximate theories intended for less tractable problems.

The analysis of periodic perturbations suggests that a persistent stochastic perturbation of vital rates will also generate a superposition of cycles of population change. The dynamics of a population subject to stochastic perturbation are also nonlinear, so again the theory has relied upon approximations. Lee (1975) pioneered the application of time-series methods to the linearized analysis of stochastic perturbations. To go beyond linearization, e.g., if the perturbations are large or have strong positive serial correlations, a higher order approximation may be used as discussed by Tuljapurkar (1990), Tuljapurkar and Lee (1997).

4. Internally Driven Cycles

The formal analysis of internally driven cycles is quite distinct from the analyses used in classical demography, and draws on developments in nonlinear dynamics (for a review of modern nonlinear techniques for dynamics, see Guckenheimer and Holmes (1983)). To start with, it is important to recognize that there are different forms of internal feedback. One class of feedback is exemplified by cohort size effects on fertility: large birth cohorts go on to have lower fertility than their parents and the opposite for small birth cohorts (Lee 1974, 1976, Wachter and Lee 1989). A second class of feedback is generated by social norms or expectations: for example, individual fertility is influenced by the average fertility in the population (Kohler 2000). A third class of feedback arises through an interaction between a population and external variables—for example, economic conditions, environmental conditions, or resources such as land holdings—and these external variables in turn influence fertility or mortality (Bonneuil 1990, 1992, 1997, Chu 1998, 1999, Feichtinger and Sorger 1990, Feichtinger and Dockner 1990, Lee 1987, Milik and Prskawetz 1996).

The formal theory of such feedbacks shares several elements that may be illustrated by considering a nonlinear version of Eqn. (1). Suppose that the net reproduction φ(a, t) in that equation changes with the population structure: for example, the fertility of individuals aged a at time t depends on the size of that cohort relative to the size of their parents’ cohort. Such feedbacks result in a functional relationship of the form

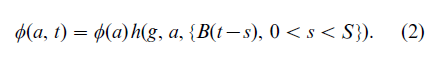
Here the function h on the right describes the effect of the other birth cohorts, born as long as S > 0 years ago, on the fertility of the cohort aged a. The parameter g controls the strength of the feedback, for example, by controlling the gradient of h. Lotka’s equation is now a nonlinear renewal equation, which can be written in abstract form as

The nonlinear operator L maps past values of births into their current value. This verbal description can be formalized suitably; for an example of the mathematical details see, e.g., Cushing (1978).

In most applications the nonlinear eqn. (3) has a constant solution, E( µ). The dynamic stability of this solution is examined by studying small deviations x(t) = B(t) – E( µ) : stability means that x(t) should decrease over time. An expansion of the nonlinearity in eqn. (3) yields a series of terms of the form

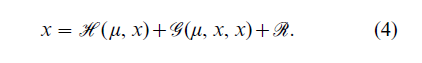
The operator H is a linear operator,J is quadratically nonlinear, and R involves higher-order nonlinear terms. Local stability is determined by the eigenvalues of the linear operator H, and these in turn depend on the elasticity of the linear response (Wachter 1991a). In typical examples, the equilibrium is locally stable when g <g*, say, but becomes unstable when g ≥ g*. Local instability means that small deviations from the equilibrium births will change with time as exp{( p + iq)t} where p > 0 and q are given by eigenvalues of the linear operator H. The local change in x(t) follows a cycle of period (2π/q). The central question now is: when such local instabilities grow and experience the nonlinear forces in equation (4), will they turn into sustained, stable cycles? If they do, increases in the parameter g past the threshold value g* will generate a sustained population cycle, called a limit cycle. Since E(µ) is still a constant solution, eqn. (3) (or its solution) is said to have undergone a bifurcation at g = g*.

For any value of g above but not far from the threshold g*, the nonlinear limit cycle may be represented by a superposition of periodic solutions to the linear part of eqn. (3). Numerical illustrations of such limit cycles are given by Frauenthal and Swick (1983). A systematic procedure for computing the amplitude, period, and stability properties of this limit cycle beyond the bifurcation point is described by Tuljapurkar (1987), and substantive applications that illustrate these computations are given by Wachter (1991b) and Chu (1998). These procedures may be extended to many other models with feedback, and provide an important part of the theory of population cycles. Other feedback mechanisms may result in a different approach to bifurcation (e.g., bifurcation in fertility level, Kohler 2000).

5. New Directions

The formal theory of cycles has moved considerably beyond classical demographic theory. The nonlinear bifurcation analysis discussed above can be considerably extended. Wachter (1994) has explored global properties of feedback models, addressing the behavior of cycles far above a bifurcation threshold. Bonneuil (1992), Prskawetz and Feichtinger (1995), and Tuljapurkar et al. (1994) show that increasing feedback can lead to more complex types of population cycles including aperiodicity and chaos. Purely internal feedbacks may not be strong enough to generate demographic cycles in human populations, but feedbacks mediated by social or external interactions may well be strong enough. The challenges that face the theory now lie in two areas: confrontation with data to test and modify theories, and the development of new models that incorporate a wider range of demographic dynamics and interaction. As yet, nonlinear cycles in human populations have not been examined in the realistic and rich way that biologists have explored cycles in the structure of laboratory populations (de Roos 1997, Cushing 1997).

Bibliography:

1. Bonneuil N 1990 Turbulent dynamics in a 17th century population. Mathematical Population Studies 2: 289–311
2. Bonneuil N 1992 Attractors and confiners in demography. Annals of Operations Research 37: 17–32
3. Bonneuil N 1997 Transformation of the French Demographic Landscape, 1806–1906. Oxford University Press, Oxford
4. Chu C Y C 1998 Population Dynamics: A New Economic Approach. Oxford University Press, Oxford
5. Chu C Y C 1999 Predator-prey models with endogenous decisions. Mathematical Population Studies 8: 55–71
6. Coale A J 1972 The Growth and Structure of Human Populations: a mathematical investigation. Princeton University Press, Princeton, NJ
7. Cushing J M 1978 Nontrivial-periodic solutions of some Volterra integral equations. Lecture Notes in Mathematics 737: 50–66
8. Cushing J M 1997 Nonlinear matrix equations and population dynamics. In: Tuljapurkar S, Caswell H (eds.) Structured Population Models in Marine, Terrestrial and Freshwater systems. Chapman and Hall, New York
9. de Roos A M 1997 A gentle introduction to physiologically structured models. In: Tuljapurkar S, Caswell H (eds.) Structured Population Models in Marine, Terrestrial and Freshwater systems. Chapman and Hall, New York
10. Feichtinger G, Dockner E J 1990 Capital accumulation, endogenous population growth, and Easterlin cycles. Journal of Population Economics 3: 73–87
11. Feichtinger G, Sorger G 1990 Capital accumulation, aspiration adjustment, and population growth: limit cycles in an Easterlin-type model. Mathematical Population Studies 2: 93–103
12. Frauenthal J C, Swick K E 1983 Limit cycle oscillations of the human population. Demography 20: 285–98
13. Guckenheimer J, Holmes P 1983 Nonlinear Oscillations, Dynamical Systems and Bifurcations of Vector Fields. Springer, New York
14. Keyfitz N 1985 Applied Mathematical Demography. Springer, New York
15. Kim Y J, Schoen R 1996 Populations with sinusoidal birth trajectories. Theoretical Population Biology 50: 105–23
16. Kohler H P 2000 Social interactions and fluctuations in birth rates. Population Studies 54: 223–7
17. Lee R D 1974 Formal dynamics of controlled populations and the echo, the boom and bust. Demography 11: 563–85
18. Lee R D 1975 Natural fertility, population cycles, and the spectral analysis of births and marriages. Journal of the American Statistical Association 70: 295–304
19. Lee R D 1976 Demographic forecasting and Easterlin hypothesis. Population and Development Review 2: 459–68
20. Lee R D 1977 Methods and models for analyzing historical series of births, deaths and marriages. In: Lee R D (ed.) Population Patterns in the Past. Academic Press, New York
21. Lee R D 1987 Population cycles. In: Eatwell J, Milgate M, Newman P (eds.) The New Palgrave; A Dictionary of Economic Theory and Doctrine. MacMillan, UK
22. Li N, Tuljapurkar S 1999a Population momentum for gradual demographic transitions. Population Studies 53: 255–62
23. Li N, Tuljapurkar S 1999b The solution of time-dependent population models. Mathematical Population Studies—J. Demog. 7: 311–29
24. Milik A, Prskawetz A 1996 Slow–fast dynamics in a model of population and resource growth. Mathematical Population Studies 6: 155–69
25. Prskawetz A, Feichtinger G 1995 Endogenous population growth may imply chaos. Journal of Population Economics 8: 59–80
26. Schoen R, Kim Y J 1994 Cyclically stable populations. Mathematical Population Studies 4: 283–95
27. Schoen R, Kim Y J 1997 Exploring cyclic net reproduction. Mathematical Population Studies 6: 277–90
28. Tuljapurkar S 1985 Population dynamics in variable environments. 6 Cyclical environments. Theoretical Population Biology 28: 1–17
29. Tuljapurkar S 1987 Cycles in nonlinear age-structured models. I. Renewal equations. Theoretical Population Biology 32: 26–41
30. Tuljapurkar S 1990 Population Dynamics in Variable Environments. Springer, New York
31. Tuljapurkar S, Boe C, Wachter K 1994 Nonlinear feedback dynamics in fisheries: analysis of the DeRiso–Schnute model. Canadian Journal of Fisheries and Aquatic Science 51: 1462–73
32. Tuljapurkar S, Lee R 1997 Demographic uncertainty and the stable equivalent population. Mathematics and Computer Modelling 26: 39–56
33. Wachter K W 1984 Lotka’s roots under rescalings. Proceedings of the Natural Academy of Sciences of the USA 81: 3600–4
34. Wachter K W 1986 Ergodicity and inverse projection. Population Studies 40: 275–87
35. Wachter K W 1991a Pre-procreative ages in population stability and cyclicity. Mathematical Population Studies 3: 79–104
36. Wachter K W 1991b Elusive cycles: are there dynamically possible Lee–Easterlin models for U.S. births? Population Studies 45: 109–35
37. Wachter K W 1994 The Cohort Feedback model with symmetric net maternity. Mathematical Population Studies 5: 25–44
38. Wachter K W, Lee R D 1989 U.S. births and limit cycle models. Demography 26: 99–115