Primate Cognition Research Paper

Shettleworth, 1998). I first consider a sample of problems that require careful attention before the fruits of the comparative approach can be tasted. Next, I review two case studies that I believe illustrate the power of the comparative approach. This review and the case studies selected are biased in two ways: Most of the work focuses on primates (because this is what the editors asked me to do, and it happens to be the taxonomic group on which I work!), and the case studies represent conceptual problems that I have explored. To alleviate the criticism that I am a primate chauvinist, let me state at the outset that for many of the examples I discuss, primates are unlikely to be unique in the capacities exposed and are often not the best group for working out the mechanistic details. They are, however, an important group for understanding problems relating to human evolution and the potential sources of our own intellectual heritage; I elaborate on this issue in the first section of this research paper. Although I focus on problems that I have worked on in some detail, such focus in no way implies that these areas are more important than others. My primary reason for focusing on the cases described in the second section is that I believe they make deep connections with studies of brain function and infant cognitive development—two disciplines that should be better connected to studies of primate cognition.

Phylogenetic Considerations About Homology and Homoplasy

A central problem in comparative biology is determining the evolutionary mechanisms underlying similarity between species. As evolutionary theorists point out, however, there are two coarse-grained categories of similarity, and each provides insights into phylogenetic patterns and the history of selection pressures. One category concerns homologies, identified as characteristics that are shared between two species because of evolution by descent from a common ancestor that also expressed the same characteristic. The second category concerns homoplasies, characteristics that independently evolved in different taxonomic groups due quite often to the process of convergence.

To illustrate the importance of this distinction, consider an example from outside of the Primate order: brood parasitism in birds (Sherry, 1997, 2000). In a wide variety of birds, breeding individuals dump their eggs into a host nest rather than rear the young on their own. The benefit to the parasites, of course, is that they only pay the cost of producing the egg, leaving the costs of rearing to the host. In one of the more carefully studied species—the brownheaded cowbird—females lay approximately 40 eggs per year and use the nests of more than 200 different host species; the large number of hosts is critical to their success because from an evolutionary perspective, such variation reduces the opportunity to develop a discriminating recognition system. Before dumping their eggs, cowbirds must scout the area, find suitable hosts, remember where they are, and then drop them off at a suitable time with respect to the host’s reproductive cycle; dumping an egg before the nest is complete or after all of the host’s eggs have been laid can lead to abandonment. Because egg dumping is the female’s responsibility, one might expect to find sex differences in memory, with females showing greater abilities than males. And if such sex differences exist, then there must be a neural mechanism underlying this behavioral difference. Analyses by Sherry, Forbes, Khurgel, and Ivy (1993) have revealed that female cowbirds have a larger hippocampus than do male cowbirds, although there are no differences in overall brain size. These results show that selection can operate on neural specializations, leading to adaptations that are well suited to particular ecological problems. One must, however, move cautiously with such interpretations because it is possible that sex differences in the hippocampus are simply present in all blackbirds (i.e., the subfamily to which cowbirds belong). If all blackbirds show a sex difference in hippocampal size, then we have an example of a homology, and claims for a selective adaptation within the brown-headed cowbird are unwarranted. To show that this sex difference represents an adaptation—one designed to meet the challenges of specific ecological pressures—comparative data are crucial.

In studies of red-winged blackbirds and common grackles— two blackbird species that raise their own young—it has been shown that there are no sex differences in hippocampal size (Reboreda, Clayton, & Kacelnik, 1996; Sherry et al., 1993). Furthermore, in the shiny cowbird, whose females parasitize over 150 host species, there is a significant size difference in the hippocampus in favor of females, whereas in the screaming cowbird in which both male and female search for a host, there is no difference in hippocampal size. These data add considerable strength to the claim that sex differences in hippocampal size are the result of selection for adaptations to current ecological conditions and that such conditions are only present in some blackbird species.

Primatologists have often aimed their comparative efforts at humans, and this is particularly the case in the study of cognition. When human and nonhuman primates show the same phenotypic patterns or characters, it is often assumed that such similarities represent cases of homology. It is possible, however, that the similarity represents a case of homoplasy. Many cases of putative homologies within the primates (e.g., face recognition; Kanwisher, Downing, Epstein, & Kourtzi, in press; Kanwisher, McDermott, & Chun, 1997; Perrett et al., 1988; Perrett et al., 1984) have been defended on the basis of plausibility—specifically, that it is unlikely for the character to have evolved twice, once in each lineage. Although this is a reasonable argument to make for primates as a group, each case must be considered on its own. It is certainly possible that some traits shared in common between two species evolved after the divergence point. Moreover, in cases in which the putatively homologous character is a behavioral trait, it is possible that the underlying mechanisms differ between species. Conversely, cases of apparent homoplasy at the behavioral or anatomical level may actually represent cases of homoplasy at the genetic level, as the revolutionary studies of hox-homeobox genes have revealed (Carroll, Weatherbee, & Langeland, 1995; Gerhart & Kirschner, 1997).

Although there are historical reasons for drawing comparisons between human and nonhuman primate cognition, there are two potential problems with this kind of focus. First, when neuroscientists look to animals for comparative data, they tend to draw classificatory boundaries with respect to higher order taxa such as animal, vertebrate, or monkey. Consequently, there are numerous books and articles on the neurobiology of spatial memory, visual attention, decision making, and categorization that speak of comparisons between humans and “animals” or “monkeys and birds.” For example, in a recent review article on the neurobiology of face perception, Haxby, Hoffman, and Gobbini (2000) state that in “the monkey [italics added], neurons that respond selectively to faces are found in patches of cortex in the superior temporal sulcus and in the inferior temporal gyrus” (p. 225). In a different article on the same topic, Tarr and Gauthier (2000) state that support “for feature maps comes from monkey [italics added] neurophysiology suggesting a topography of features in inferior temporal cortex (IT) and from human fMRI [functional magnetic resonance imaging] studies indicating that across a single task, different stimuli selectively activate different regions of the ventral temporal cortex” (p. 764). In each of these quotes, the monkey is the rhesus monkey. Although this particular species has been the model animal for studies focusing on the neurobiology of vision, we should be careful in assuming that rhesus are representative of primates, including both closely and distantly related species. For example, because some primates have a limited suite of facial musculature (Huber, 1931), they rarely produce facial expressions, and when they do, they have a small repertoire. Furthermore, although some primates such as rhesus exhibit the characteristic inversion effect shown in humans (i.e., faster and more accurate recognition of upright faces than of inverted faces), not all species do, even though faces clearly play an important role in their social behavior (Weiss, Ghazanfar, Miller, & Hauser, 2002). As I document in the following discussion, there are often important differences between species—even within the same genus—and such differences are informative with respect to the selective pressures on brain organization. Although one might reasonably ask whether any animal is capable of a cognitive computation that is characteristically human, a far richer evolutionary account would not only explore whether nonhuman animals can carry out the computation, but which species and why. Thus, in cases in which we share with other animals a particular computational ability, is this because of phylogenetic inertia, because of similar social and ecological pressures, or both? By thinking about socioecological pressures we are more likely to pinpoint appropriate species for our comparative analysis. Second, studies of cognitive evolution should also focus on similarities and differences between nonhuman primates—independently of the patterns obtained for humans. This is important because it allows us to map patterns of primate mind-brain evolution onto existing phylogenies that have used molecular, anatomical, behavioral, and ecological characters (Allman, 1999; Deacon, 1997; Deaner, Nunn, & van Schaik, 2000; Di Fiore & Rendall, 1994).

In the literature reviewed in the following discussion, it should become apparent to the reader that our understanding of many cognitive traits is restricted to only a handful of species. For example, although we know a great deal about asymmetries in hand use—and in coarse-grained anatomy for a number of primate species—our knowledge of behavioral and neurophysiological asymmetries associated with the perception and production of communicative signals is largely restricted to two macaque species (Macaca mulatta, Macaca fuscata) and chimpanzees (Pan troglodytes; Weiss et al., 2002). As a result, our ability to draw inferences about the patterns of evolution is minimal. An important goal of this essay, therefore, is to draw attention to what we know about the few species that have been studied; I also hope to inspire others to collect the relevant data on other species.

Comparative Methods for Comparative Cognition

Aproblem facing students of human infant and nonhuman animal cognition is that we cannot use language to ask about the thoughts and emotions underlying their behavior. In response to this problem, researchers have developed clever methodologies. Often, however, the methods used are designed for one species or a specific age group, and thus either cannot or have not been applied to other species or age groups. Additionally, in cases in which the same method has been applied to different species or age groups, a question arises as to the appropriateness of the method in asking questions about similarities or differences in cognitive abilities or competences. If we are to understand how the minds of different species evolved, then we must not only acknowledge these methodological problems, but also systematically confront them in our studies. Macphail (1987a, 1987b) sounded this warning almost 15 years ago, and the problems are still with us today.

On an extremely general level, there have been two methodological approaches to the study of animal cognition. On the one hand are studies typically run in a laboratory environment that involve some kind of training to shape an animal’s initial behavior. After being trained to make a certain kind of response, subjects are often tested on generalization conditions designed to reveal what they have learned or can learn beyond the initial training period. On the other hand are studies run both in the laboratory and in the wild that tap spontaneous cognitive capacities. Here, the goal has been to understand how animals use species-typical behavior to solve problems. Both approaches are associated with benefits and costs. Independently of such methodological economics, however, it is clear that if we are to understand what neurocognitive processes mediate a particular behavior and whether such processes are similar or different across species, then we need tools that can be applied to different species with little or no change. This point has been made before but requires repeating because of the potential pitfalls associated with making assessments of differences and similarities in performance on a task. There are two critical questions or problems. First, does species or age-group Aperform worse than does species or age-group B because Alacks a particular ability or because the task fails to engage a species-typical or age-appropriate motor response? For example, A might fail not because it lacks the conceptual resources to solve the task but because A lacks the requisite motor competences. Second, when species or age-group A performs as well or in the same way as species or age-group B, is this because members of A and B are solving the problem in the same or a different way? It has often been assumed that similarities in performance are guided by similarities in the underlying mechanism, but this need not be the case.

An elegant example of the second problem comes from the study of animal cultures or traditions. In a variety of species, one finds that members of one population perform a behavior not seen in other populations of the same species. In such cases, if differences in ecology or genetics can be ruled out as causes of interpopulation differences, then it seems reasonable to conclude that such differences arise due to learning. Of interest to those studying such traditions is how they were invented, passed on to others, and then maintained over time (Byrne & Russon, 1998; Galef, 1992; Heyes & Galef, 1996; Tomasello, Kruger, & Ratner, 1993; Whiten & Ham, 1992). Studies of wild chimpanzees highlight the extraordinary variation in tool use technology seen among populations that lack significant genetic or ecological differences, but studies of chickadees highlight the importance of conducting carefully controlled experiments to determine how homogeneity in the expression of a behavior emerged within the population. Sherry and Galef (1984, 1990) explored the famous studies of Fisher and Hinde (1949) on milk bottle opening in blue tits by running experiments with black-capped chickadees in captivity. The goal of these experiments was to assess whether the homogeneity among blue tits emerged because of imitation as opposed to some other transmission mechanism. One set of naive individuals watched as a demonstrator removed foil from a milk bottle and then skimmed the cream. These individuals were then placed alone in a cage with a foil-capped milk bottle. A second group of naive individuals was first placed alone in a cage with an uncapped milk bottle; the foil was placed next to the bottle. In the next session, these individuals were placed alone in a cage with a foil-capped milk bottle. When Sherry and Galef compared the speed with which individuals in these two groups learned to remove the foil from the milk bottle, they found no statistically significant differences. These studies show that what may appear to be an example of imitation (e.g., all the blue tits learned by copying from one genius tit to remove the foil) or some other form of social learning may in fact not be social at all. In the chickadee case, one group clearly learned from a demonstrator, but the second group learned by deduction—by seeing the foil next to the bottle and skimming the milk, such individuals solved the problem by playing the equivalent of Jeopardy: The answer is Drinking milk with foil next to the bottle. The question is How do you drink milk from a foil-capped bottle?

I emphasize these two problems throughout the rest of this research paper. In addition, I focus on methods that involve little to no training and that can be used across a variety of primate species with little to no change; in many cases, these techniques are likely to be effective with nonprimate animals as well, thereby broadening the depth of our comparative analysis. Most important is that because the methods described have been used with human infants and can readily be used in neurophysiological preparations with animals, we are in an excellent position to forge a link between ethologists, cognitive developmentalists, and neuroscientists.

Domain-Specific Systems of Knowledge

Some might claim that evolutionary psychologists have an obsession with modularity—or with massive modularity, as Jerry Fodor (2000) has recently put it. In fact, Fodor’s recent treatment of modularity and his explicit criticisms of evolutionary psychology might come as a surprise given that the man has long been a champion of modular views of the mind anchored by a strong nativist perspective (Fodor, 1983). What is at stake in this debate, as well as a parallel one with those who think that the mind is merely a collection of general learning mechanisms, is how nature has carved the mind into specialized mechanisms that come equipped with knowledge of the world. As Fodor correctly points out, some evolutionary psychologists have mistakenly assumed that a commitment to domain specificity and modularity is a commitment to innateness. These are orthogonal issues. Of concern here—and a mediating force in the selection of empirical cases in the following discussion—is the hypothesis of category or domain specificity.To say that the mind consists of domain-specific systems is to claim that different domains of knowledge are guided by specific learning mechanisms or computations, often associated with dedicated neural circuitry. As I have argued elsewhere (Hauser, 2000), building on the views of Fodor (1983, 2000), Pinker (1994, 1997), and others (Caramazza, Hillis, Leek, & Miozzo, 1994; Carey & Spelke, 1994; Dehaene, 1997; Hirschfeld & Gelman, 1994), the domain-specificity perspective is not only a powerful theoretical argument, but is also a highly effective research strategy because it forces one to explore how particular features and principles guide and constrain the organization and acquisition of knowledge. It is simply an empirical question whether it is domain-specific systems all the way down or some combination of domainspecific and domain-general mechanisms and whether domain-specific or -general mechanisms are equipped with innate knowledge, and if so, what this knowledge is and how it permits learning of a certain kind. The domain-specificity perspective has already played a critical role in studies of patients with brain damage (e.g., cases of category-specific deficits for fruits, vegetables, faces; Caramazza & Shelton, 1998), in neuroimaging experiments of normal human adults (Kanwisher et al., in press), and in understanding conceptual development in infancy and early childhood (Carey & Spelke, 1994; Keil, 1994). It is high time that more students of animal behavior reap the benefits of this perspective; some already have (Cheney & Seyfarth, 1985; Gallistel, 1990; Hauser, 1997; Santos, Hauser, & Spelke, 2001).

To illustrate, consider the domain of spatial knowledge.We know from hundreds of studies of insects, fish, birds, and mammals that animals are equipped with two basic mechanisms for navigating in the world: dead reckoning, whereby the speed and distance traveled are automatically updated and used to find the most direct route to a target location; and piloting, whereby distinctive landmarks are used to find specific targets within a highly familiar area (Gallistel, 1990; Healy, 1998; Shettleworth, 1998).When animals use landmarks, certain features are more reliable than others are.Thus, for example, if home is located next to a white birch tree, what is relevant about the birch is its specific shape and consistent location but not its color or orientation. After all, if the birch falls over or undergoes a color change due to a shift in the seasons, it is still a reliable landmark. To explore whether animals are able to conjoin information from two different properties of a spatial environment, Cheng (1986) set up an experiment with rats. In the first condition, subjects were first placed in a rectangular room with four white walls and then shown a baited corner. Next, they were spun around with their eyes closed in order to disorient them. When they were released, subjects searched for the food in either the correct (i.e., baited) or geometrically opposite corner. These data suggest that rats can use the geometry of the room to find a target location. In the second condition, the rectangular room consisted of three white walls and one black wall. Although the task was the same, subjects were provided with a potentially salient, nongeometric feature (i.e., a colored wall) that could serve as a landmark. Under these circumstances, however, rats searched exactly as they did in Condition 1, looking in either the correct or geometrically opposite corner. What these results show is that rats are unable to conjoin geometric with nongeometric features in the context of spatial disorientation, leading Cheng to conclude that rats are equipped with a geometric module—one that is highly encapsulated with respect to information coming in from other domains. It is unlikely that this kind of question and experimental design would have been set up outside a domain-specificity perspective.

An interesting twist on Cheng’s results—one emphasizing the importance of comparative work—comes from studies of human toddlers and adults, as well as studies of chickens and rhesus monkeys. Specifically, Hermer and Spelke (1994, 1996; Hermer-Vazquez, Spelke, & Katsnelson, 1999) showed that when toddlers are run on Cheng’s disorientation task, they perform exactly like rats—searching in the correct or geometrically opposite corner even when there are highly salient landmarks (e.g., a tree in one corner and a large plastic gnome in the other). However, when adults are run on this task, they perform like rats and toddlers in the all-white room, but search primarily in the correct corner when given a landmark. What Hermer and Spelke have argued is that in order to conjoin geometric and nongeometric features following disorientation, language is necessary. Specifically, adults solve the disorientation problem by saying something like The baited location is to the right of the black wall. When adults are prevented from using language by imposing a verbal shadowing task, they go back to looking like toddlers and rats. If language is necessary for conjoining geometric with nongeometric features, then clearly no animal should solve this task. Although Cheng’s results would seem to support this claim, studies of chickens (Vallortigara, Zanforlin, & Pasti, 1990) and rhesus monkeys (Gouteux, Thinus-Blanc, & Vauclair, 2001) do not. Specifically, both of these species solve the disorientation task when landmarks are provided, although training was involved in both studies. Critically, then, these studies show that although language might be used by humans to conjoin geometric and nongeometric features, it is certainly not necessary. Whether there is a geometric module in the Fodorian sense depends on the species, as well as on the task, thereby emphasizing both the importance of cross-species comparisons and the application of different methods.

How to Study Cognitive Evolution: Two Test Cases

The Construction of a Number Sense

Children have the capacity to acquire the number system. They can learn to count and somehow know that it is possible to continue to add one indefinitely. They can also readily acquire the technique of arithmetical calculation. If a child did not already know that it is possible to add one indefinitely, it could never learn this fact. Rather, taught the numerals 1, 2, 3, etc., up to some number n, it would assume that that is the end of the story” (Chomsky, 1988, p. 167).

If there is anything that is distinctively human, it is our capacity to represent quantities with symbols, to use such symbols with abstract functions or operators, and to put these elements together to create the language of mathematics. Granted, not all cultures have the kind of formal mathematics that some of us learned in school. However, all cultures have a system of symbolic quantification, including number words and grammatical mechanisms for distinguishing (minimally) one object from many (Butterworth, 1999; Dehaene, 1997). Furthermore, all cultures care about quantification because— by our nature as humans—we have a sense of fairness (Ridley, 1996; J. Q. Wilson, 1987) that mediates exchange and sharing, whether it is over mongongo nuts and bush meat or high-tech stocks. Moreover, when one explores some of the ancient systems for representing numbers, one uncovers an extraordinarily nonrandom pattern: All cultures have distinctive and rationally assigned symbols for the numbers one, two, and three (sometimes four), but then change to a different notational system for numbers greater than three or four. Thus, for example, the Romans developed the systematically transparent system that mapped one to I, two to II, and three to III, but then modified the system at four with the introduction of a new symbol (V)—and thus the introduction of a new rule—to create a new pattern (IV). Similarly, in English we use the words first, second and third, but then shift to using fourth, fifth, sixth, and so on, or -th all the way up. Why shouldn’t we write the Roman numeral for four as IIII, or use the word fourd or fourst? What privileges the numbers one to three or four? Such consistency across cultures suggests that humans are endowed with a number sense, a domain-specific system that is universally present and forms the foundation of our mathematical talents. It also suggests something special about the numbers one through four as opposed to numbers greater than four. Of concern here, then, is what this representational mechanism is like, how early in life it can be detected, how it mediates the child’s path to numerical competence, and whether this capacity is uniquely human or shared with other animals? If we share with other animals a number sense, then what have the millions of years of biological and cultural evolution added that enable us to carry out computations that no other animal can and to develop elegant and often esoteric mathematics that can only be enjoyed by those rare human beings with a passion and gift for higher mathematics? To address these questions, I first provide a brief review of some of the relevant work on human infants, focusing on some of the earliest evidence for spontaneous numerical representations; I focus on infants in particular because this age group provides the best opportunity to explore the hypothesis that biology has provided us with a numerical foundation that is then elaborated and enriched as a function of language as well as of other cognitive resources and experiences. Next I look at the evidence for numerical computations in nonhuman animals, contrasting studies that involve training with those that do not. I conclude with a brief discussion of what is currently known about the neural basis of number representation in human and nonhuman animals; then I review how work in this area forces a reconsideration of the theory that has been developed to explain nonlinguistic numerical representations.

Number Representation in Human Infants

If in fact some aspects of our number sense are universal, then we ought to pick up traces of this capacity in human infants. According to one view, championed by such cognitive scientists as Fodor (1975) and Pinker (1994, 1997), not only should infants have some of the core principles underlying our number sense, but such principles should also be continuous with the capacity observed in adults. This is the continuity thesis of human cognitive development. According to a second view articulated most recently by Carey and Spelke (in press), we are born with a core set of principles that put into play our capacity to acquire mathematics, but over development we acquire new representational resources that literally transform the earlier representations; this is the discontinuity thesis. According to either view, it is essential to establish what the infant is handed by biology—with respect to its capacity to compute numerosities—and how such mechanisms mediate subsequent learning.

During the 1980s, several developmental psychologists asked whether human infants could discriminate stimuli based on their numerical differences (Antell & Keating, 1983; Starkey & Cooper, 1980; Starkey, Spelke, & Gelman, 1990; Strauss & Curtis, 1981). In the classic design, an experimenter presented an infant with stimuli of a constant number, but with variability introduced in terms of either the kind of objects presented or the spatial arrangement of items such as dots on a monitor. Thus, for example, an infant would be habituated to slides consisting of two dots randomly arrayed within the frame and then would be tested with slides consisting of either three dots or two dots presented in a new spatial arrangement. Results from these experiments suggested that young infants were sensitive to different numerosities and were capable of discriminating one from two, two from three, and in some experiments, three from four. Moreover, work by Spelke and colleagues (Spelke, 1979; Spelke, Born, & Chu, 1983) indicated that the infant’s representation of number appeared abstract and amodal as evidenced by the fact that they classified two dots and two beeps as the same, but two dots and three beeps as different.

In 1992, Wynn published an important paper suggesting that infants could not only discriminate numerosities, but could also operate over them, carrying out simple additions and subtractions. Taking advantage of the expectancy violation procedure developed to explore visual perception, Wynn firstfamiliarized4-to5-month-oldinfantswithanemptystage and with a stage showing either one, two, or three Mickey Mouse dolls. Next she ran infants on one of three versions of a test trial involving the addition of one object to another. In the expected or possible test, the infant watched as one Mickey was placed on the stage, an occluder raised to hide Mickey, a second Mickey introduced behind the occluder, and then the occluder removed to reveal two Mickeys (i.e., 1+ 1= 2). This is an expected or possible outcome if the infant sees the first Mickey on the stage, maintains a representation of one Mickey behind the occluder, updates this representation to two Mickeys when the second is introduced, and then maintains this representation until the occluder is removed revealing precisely two Mickeys. In the two unexpected or impossible test trials, the presentation was identical to the expected versionexceptthatwhentheoccluderwasremoved,theinfant saw either one or three Mickeys (i.e., 1 + 1 = 1 or 3). If—as sketched for the expected test trial—infants store a representation of two Mickeys when the occluder is in place, then when the experimenter removes the occluder and reveals either one less or one more Mickey, they should look longer than they do when the outcome is precisely two Mickeys; this is exactly what Wynn observed in her studies. She also observed a similar difference in looking time in a subtraction event, contrasting a 2 – 1 = 1 outcome with a 2 – 1 = 2 outcome (Wynn, 1992). Wynn concluded that infants have an innate capacity to compute simple additions and subtractions.

Since Wynn’s publication, there has been a flurry of activity by infancy researchers interested in the development of numerical representations. Several issues are at stake. First, to what extent can the infant’s representation be considered numerical? Second, given differences in methodological procedures across studies, are experimenters testing the same thing? Third, what ontogenetic changes arise with respect to the representation of number? What is the role of innate constraints on learning and what kinds of experience are either necessary or sufficient with respect to developing the core principles of a number system (e.g., one-to-one correspondence, abstract, ordinal relationships, cardinality; Gelman & Gallistel, 1986)? Finally, how—from a computational perspective—do infants compute numerosities, and are there differences between small and large numbers, as well as between approximate and exact calculations?

Although the level of activity in this area has been high, it is difficult to provide a concise and unambiguous summary at this point due to differences between studies in experimental design, behavioral assays, and stimuli presented. Thus, some studies have used a looking time technique, whereas others use a reaching procedure; some use computer generated displays, whereas others use real objects; some require the use of working memory, and others do not; and so forth. To illustrate, consider a set of studies that have used the looking time technique. Following up on Wynn’s original work, Simon, Hespos, and Rochat (1995) provided a replication, but also an interesting twist. By the age of approximately 5 months, although infants appear sensitive to the number of objects placed behind an occluder, they do not appear sensitive to the properties or kinds of object. Thus, if infants see two identical Ernie dolls (from Sesame Street) placed behind an occluder, they look equally long at an outcome of two Ernie dolls as they do at an outcome of one Ernie and one Bert or two Berts. These results fit in nicely with recent work by Xu and Carey (1996, 2000; Xu, Carey, & Welch, 1999) suggesting that it is not until the age of approximately 12 months that infants discriminate objects based on their properties or kinds (for an opposing position, see Needham and Baillargeon, 2000). Koechlin, Dehaene, and Mehler (1997) then showed that when infants detect a violation in number, they do so even when the spatial arrangement of the objects changes. Thus, if objects are rotated on a disc (a lazy Susan), infants look longer at outcomes with different numbers of objects but not different spatial arrangements of the same number of objects. Uller, Carey, Huntley-Fenner, and Klatt (1999) also provided a replication of Wynn’s original design but showed that the outcome depends on whether the infant first sees one object on the stage followed by occlusion or starts by seeing an empty stage followed by the introduction of two objects behind the occluder. Specifically, although 5-month-old infants looked longer in the unexpected test trials of an object-first 1 + 1 condition (i.e., outcomes of 1 and 3; Wynn’s original design), they did not discriminate between these outcomes until the age of 8 months when tested on a screen-first design. These results suggest that independently of the content of the infant’s representation, working memory plays a crucial role; the object-first design demands only a single update in memory, whereas the screen-first design requires two.

All of the work reviewed thus far suggests that infants can discriminate small numerosities on the order of three to four. When we consider all of these studies together, however, we are left with a problem. Whereas the earlier experiments on number involved presentations that did not recruit working memory (i.e., the stimuli to be discriminated were always in view), the more recent experiments using expectancy violation do. Although it might be the case that the same mechanism underlies all of the findings to date, it is possible that there are different mechanisms and that some of the findings can be better explained by a system that is not strictly numerical, but rather tied more generally to what infants know about objects, especially under occlusion (Leslie, Xu, Tremoulet, & Scholl, 1998; Simon, 1997; Simon et al., 1995). Some of the most recent work in this area speaks directly to this problem.

In the early work on number representation in infants, the experimental stimuli were poorly controlled with respect to factors that might covary with number, and thus enable the infant to discriminate on the basis of features other than numerosity. Thus, in the original work by Starkey and colleagues, although infants appeared to discriminate between stimuli consisting of two versus three dots, they might have also discriminated between these stimuli on the basis of spatial extent, contour, or density. In a study by Mix, Levine, and Huttenlocher (1997) that provided more stringent controls for these factors, there was no evidence that infants were discriminating on the basis of number; rather, findings suggested that infants discriminated based on contour dimensions. However, in another study with even more careful controls, Xu and Spelke (2000) showed that infants could discriminate 8 from 16 dots but not 8 from 12 dots. In this study, number was the only relevant dimension. Xu and Spelke argued that in this particular task, infants were discriminating on the basis of ratios, and thus that they were capable of computing 2:1 but not 3:2. If correct, this suggests that on some tasks at least, infants can discriminate large numbers but are subject to the constraints associated with Weber’s law—that is, when infants discriminate stimuli on the basis of large numerosities, they are subject to the effects of distance (numbers that are further apart on the number line are more readily discriminated) and magnitude (holding the difference between two numbers constant, larger numbers (e.g., 125 and 126) are more difficult to discriminate than are small numbers (e.g., five and six; Moyer & Landauer, 1967). Along similar lines, a study by Wynn and Chiang (1999) has shown that whereas infants succeed (look longer at the unexpected condition) on a 1 + 1 = 2 versus 1 task, they fail at a 5 + 5 = 5 versus 10 task.

Complicating matters further are three additional studies with human infants using three completely different techniques. Feigenson, Carey, and Hauser (2001) attempted a replication of Wynn’s original findings with Mickey Mouse dolls, but used LEGO blocks that could be built in such a way as to explicitly control for area or volume. Under these more stringent conditions, results showed that infants looked longer when the outcome violated the expected volume or area, but not when it violated the number of objects. Thus, although infants might be sensitive to number, under the conditions tested, they are more sensitive to changes in volume and area. In a study by Wynn (1996) designed to explore whether the infants’ representation of number was restricted to discrete visual or auditory objects, infants were habituated to a puppet that jumped in bouts of two or three hops. Thus, for example, one group of infants watched as a puppet jumped in a cycle of two up and down hops, paused, two more up and down hops, then paused, and so on. After they reached a criterion level of habituation, they were presented with the same puppet, who now hopped in a cycle of either two or three hops. Only when the number of hops changed did the infants dishabituate; this pattern was obtained in the face of controls for overall duration of the hops as well as interhop intervals. These results suggest that infants can discriminate two from three both for discrete objects and for events. In a third and final test variant, Feigenson et al. (2002) presented infants with a two-choice box task, originally developed by Hauser, Carey, and Hauser (2000) for rhesus monkeys (discussed later in this research paper). In general, infants watched as an experimenter sequentially placed different numbers of crackers into each of the two opaque boxes and then allowed the infant to search and retrieve the crackers in one box; for example, the infant might see the experimenter place one cracker into one box and then two crackers into the second box. Thus, if infants prefer more crackers over fewer crackers, they should selectively search in the box with more. Results showed that infants selectively preferred the box with two crackers over one and three over two, but showed no systematic preference for four versus three as well as for six versus three. Moreover, when number was systematically tested against surface area (e.g., one cracker vs. two crackers equal in surface area to one), infants selected the box associated with the larger surface area. Thus, in parallel with the work by Mix and colleagues, infants at this early age and in these particular tasks appear to weight volume and surface area over number.

These more recent results raise several important points. First, the work by Feigenson et al. reinforces the point made earlier that in order to claim that infants or any other nonlinguistic creature discriminates stimuli on the basis of their numerical differences, one must eliminate all other possible factors such as volume, contour, density and so forth. Second, Wynn’s results suggest that if infants do in fact have a number sense, that it may—under some circumstances—be quite abstract (i.e., capable of computing over discrete objects and events). Third, several of the results reported in the preceding discussion suggest that when infants discriminate stimuli on the basis of number, they can do so precisely if the numbers involved are less than about four. If, as implicated by the work of Xu and Spelke, infants’ numerical abilities were simply subject to Weber’s law, they should have no problem with six versus three (Feigenson et al., 2002) as this reduces to a ratio of 2:1, which they pass when the number of cookies is one versus two.

These data raise one of two possible interpretations. Either these tasks are tapping different mechanisms, or there is one mechanism that is differentially effected by each of the tasks. As I discuss more completely later in this research paper, it is possible that there is one system involved in precisely computing small numerosities, a second system for approximately computing large numerosities, and a third system for precisely computing large numerosities. Rather than explicate these possibilities here, I turn next to work on animals. This work is not only critical to our understanding of number representation in humans—both infants and adults—but is also important because much of the theory derives from this work.

Number Representation in Animals: Why Might Selection Favor Numerical Computation?

There are two ways to motivate work on numerical representation in animals. On the one hand, we can ask whether there are socioecologically significant situations in which animals might profit from or require numerical computations. If so, then given sufficient variation between individuals and the coupling between computational capacity and reproductive success or fitness, selection might favor such capacities. On the other hand, we can ask whether—independent of selection for such capacities in nature—animals are capable of learning numerical discriminations and operations. Here I discuss the first approach, briefly reviewing the kinds of conditions that might select for a capacity to compute number or quantity. In the next section I turn to the second approach and show how training experiments have revealed an underlying capacity for number quantification. Subsequently, I show how we can unite both approaches to conduct experiments that tap spontaneous abilities for number representation.

There are at least three coarse-grained contexts in which one might expect to find evidence of a capacity for number representation: care of young, feeding competition, and intraor intergroup aggression. We know, for example, that in species that produce multiple young per litter or clutch, the allocation of parental care or investment depends critically on the number of young—both presently available and to be produced in the future (Clutton-Brock, 1992; Trivers, 1972). However, based on studies with birds, and especially brood parasites (Davies, 2000; Kilner, Noble, & Davies, 1999), it appears that parents do not adjust the amount of care allocated as a function of the exact number of young present. Rather, the allocation of parental care seems to be an approximate affair. In a similar vein, although a wide variety of avian species cache their food, often concealing and then retrieving thousands of seeds in thousands of different locations, there is no evidence that such individuals recall the precise numbers; rather, they recall an approximate number of seeds from an approximate number of locations (Balda, Kamil, & Bednekoff, 1997; Vander Wall, 1990). To push further, although studies of optimal foraging (Stephens & Krebs, 1986) clearly show that animals are highly sensitive to the energetic returns from different food patches, they do not appear to be calculating the precise number of food items in a patch, but rather the relative rates of return in one area as opposed to another (Ydenberg, 1998). Finally, although a coalition of two animals typically outcompetes an animal on its own and large groups outcompete smaller groups, there is no evidence that the precise number of individuals in one coalition or one group is used to assess competitive advantage; again, it is the relative number of individuals that seems to count (Harcourt & de Waal, 1992). These data suggest that if animals naturally have a system for numerical representation, then it is one that computes numbers approximately and not precisely.

In contrast to the work discussed thus far, recent experimental work on lions and chimpanzees suggests that under conditions of intergroup competition, individuals might assess the number of competitors prior to deciding whether to attack or flee. McComb, Packer, and Pusey (1994) presented lion prides with playbacks of roars from a single individual or three individuals. The extent to which the listening pride approached the speaker or roared back was contingent upon the number of individuals roaring, with the most aggressive response elicited by the simulation of three intruders. Moreover, the response to one versus three intruders was mediated by the number of lions in the pride, with stronger responses coming from larger prides. Like lions, chimpanzees are also confronted with threats from neighboring communities. Based on over 40 years of field research from sites all over East and West Africa, observations suggest that when chimpanzees from one community encounter chimpanzees from a foreign community, they will attack and kill the intruder if the ratio of adult males is 3:1 in favor of the attacking party. To test this observation, M. L.Wilson, Hauser, and Wrangham (2001) ran a series of playback experiments. Specifically, chimpanzee parties from the Kanyawara community in Kibale National Park, Uganda were presented with playbacks of a pant-hoot from a foreign adult male. When the party consisted of adult females and their offspring but no adult males, subjects stayed still or moved in the opposite direction from the speaker, and they remained completely silent (Figure 20.1). When parties consisted of at least one to two adult males, individuals approached the speaker about 50% of the time but did so silently. In striking contrast, when the party consisted of three or more adult males, individuals always approached the speaker and did so while calling loudly.

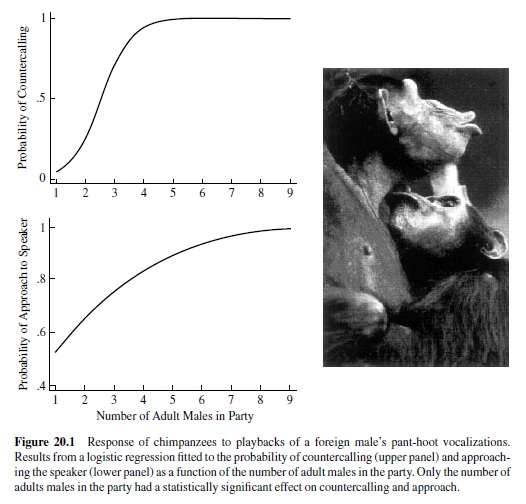
These results suggest that like lions, chimpanzees in large parties have a competitive advantage. When the number of adult males exceeds two, there are significant benefits (or possibly low costs) associated with launching an aggressive attack on a foreigner. Given the limits of the behavioral assay (i.e., approaching the speaker, calling back to the playback), it appears that chimpanzees have the capacity to discriminate between no adult males, one to two adult males, and three or more adult males. Whether they can make more fine-grained discriminations (e.g., between one and two adult males or between three and four) remains to be explored, and may require different testing procedures.

In sum, there is ample evidence that animals can spontaneously compute the quantity of objects in the environment, be they animate or inanimate. What these studies fail to illuminate is the extent to which the capacity to compute quantities is based on precise numerical calculations, approximate numerical calculations, or rough estimates of quantity that have little to do with the more formal and abstract properties of a number system. The following two sections shed some light on this problem.

Number Representation in Animals: Extracting the Substrate Through Training

There is a rich literature on number in animals based on classic operant techniques. This work, which started over 40 years ago, was intimately tied to research on timing (Church & Boradbent, 1990; Gallistel, 1990; Gibbon, 1977; Staddon & Higa, 1999). In the work on timing, results from common laboratory animals (rats and pigeons) demonstrated that subjects could represent temporal intervals and use such representations to compute complex operations that are isomorphic with division and subtraction. Moreover, work at the neurobiological level (reviewed in Gibbon, Malapani, Dale, & Gallistel, 1997) revealed a tight coupling in such animals between behavioral measures of timing and activation of basal ganglia and cerebellum. For example, lesioning of the nigrostriatal dopaminergic system of the basal ganglia greatly reduced the accuracy of interval timing in rats, whereas administration of dopamine can reinstate such accuracy following the lesion; it is interesting that recent work on patients with Parkinson’s disease reveals deficits in timing and corresponding (correlated) imbalances in dopamine.

Given that animals can operate on temporal intervals, it is clear that they have the capacity for mathematical operations. The question of interest here is whether they can generate distinct representations of number and use these to control behavior. As Gallistel (1990) has pointed out in his review of this literature, a minimum criterion for representing number is the capacity to form a one-to-one mapping between numerosity (events or objects) and brain circuitry responsible for controlling behavior. Since this work started, there has been little debate concerning the ability of animals to discriminate on the basis of numerical differences between stimuli but considerable debate concerning how number is represented—in particular, whether it is digital and precise (one-to-one correspondence between object or event and a symbol) or analog and approximate. In the classic studies on rats (Mechner, 1958; Platt & Johnson, 1971), experimenters presented subjects with two response levers, A and B. Subjects had to learn that on some proportion of trials, pressing Lever A N number of times followed by pressing Lever B once delivered food. On the remaining trials, pressing Lever A N + 1 times delivered food. Results showed that as the number of target responses increased, so did the degree of error—that is, although the median number of presses by the subject corresponded quite well to the target number, as the target number’s value increased, so did the variance. These studies, together with dozens more, have shown that subjects can discriminate (a) large numbers approximately; (b) stimuli based on number, time, or both simultaneously; and (c) the number of motor responses (lever presses or key pecks) or audio-visual stimuli (tones or light flashes). Moreover, these studies have shown that the subject’s capacity to discriminate on the basis of number of responses or stimuli is not affected by motivational state, the mechanics of depressing a lever (i.e., how long it takes, how hard it is to move it), or the combination of stimuli from two different modalities (e.g., summing the number of sound bursts and light flashes).

Using the same classic techniques, studies of nonhuman primates have generally revealed comparable abilities (Olthof, Iden, & Roberts, 1997; Rumbaugh & Washburn, 1993; Thomas, Fowlkes, & Vickery, 1980; Washburn & Rumbaugh, 1991). A recent study by Brannon and Terrace (1998, 2000), however, stands out because of the degree to which the experimenters controlled for potentially confounding variables and the extent to which subjects spontaneously generalized from a small set of numerosities to a larger set, providing evidence that they can represent the numerosities one through nine on an ordinal scale. In the training phase, three rhesus monkeys were reinforced for responding to the numerosities one, two, three, and four in ascending, descending, or nonmonotonic numerical order (i.e., 3- > 1- > 4- > 2). The stimuli—clip art images positioned within a frame—were presented on a touch-sensitive screen. Each of the four different frames appeared in a different relative position on the screen across trials, and in no trial could the subject respond in the correct order unless it had extracted the correct numbers and their ordinal relations. Thus, for example, on some trials the area of the frame covered by one object was less than two, which was less than three, which was less than four; on other trials, however, the frame with one object was larger than the frame with four objects; under these circumstances, only the number of items within the frame can be used to pick out the correct response sequence.

Subjects trained on the ascending or descending pattern were readily able to order novel pairs of the numerosities 1- > 4; the subject trained on the nonmonotonic pattern never learned the task. For subjects trained on the ascending but not the descending order, there was clear evidence of generalization to novel pairings of the numerosities 5- > 9. Based on the accuracy of their responses as well as reaction time, the rhesus monkey’s performance is consistent with Weber’s law as evidenced by the fact that subjects showed distance and magnitude effects. Thus, for small numbers and large differences between pairs, accuracy was high and reaction time was low; for large numbers and small differences between pairs, accuracy was low and reaction time was high. These results—together with earlier work on rats and pigeons— suggest that animals represent number on an ordinal scale but that their representation is in the form of an analog magnitude with scalar variability.

Acompletely different training approach to the problem of number representation in animals comes from work involving apes that have been reared by humans and taught the meaning of Arabic numerals. In the standard setup—exemplified by the work of Matsuzawa (1985) and Boysen (Boysen & Bernston, 1989)—subjects are trained to make a one-to-one association between an Arabic numeral and the corresponding quantity of a particular object, usually food. Early in training, only a few numerals are presented, and gradually, new objects of the appropriate quantities are introduced so that the subject learns to generalize across objects; this is critical, of course, because subjects must learn that number is an abstract concept independent of the type of object or objects to be enumerated. A characteristic of all of these studies, including Pepperberg’s (1994, 2000) work on an african gray parrot, is that each subject requires an immense amount of training before it can master the correspondence between symbol and quantity; even when subjects have mastered a subset of the integer count list, they never generalize with respect to new symbols.Thus, for example, Matsuzawa’s star chimpanzeeAi required as long to learn the first half of the integer count list as the second half, and when she learned the quantity associated with one symbol, the relationship appeared approximate rather than precise. Thus, when she had learned the Arabic numerals 1, 2, 3, and 4, her understanding of 4 was four or more rather than precisely four.

These criticisms of the work on number in apes should in no way take away from the extraordinary capacities that have been demonstrated (Boysen, 1997). Thus, for example, these chimpanzees can order the numbers within the count list, understand cardinality, add either the number of objects or Arabic numerals in one box with those in another to come up with the precise sum, and determine the equivalencies of fractions (e.g., half an apple and half a glass of water). In a recent experiment by Kawai and Matsuzawa (2000), one subject was first trained to press between three to five numerals in their ordinal sequence. In the next phase, as soon as the first numeral was pressed, the others were occluded by a white square, thereby requiring the subject to recall the numerals, their ordinal relations, and their spatial positions. With the actual numbers no longer in view, this subject pressed the squares corresponding to the correct numbers. These remarkable studies show that chimpanzees can learn the integer count list, and that when they operate over these symbols, their performance looks exactly like our own under the same conditions. The problem is that the nature of their underlying representation is at some level very different from our own—that is, when young children learn the integer count list, they appear to learn it first as a meaningless list, with only the most primitive understanding of what each number word means. Thus, they start by understanding that one means one, but that two, three, four, and so on mean more than one. Gradually, they build an understanding of two, three, and four, and then the system explodes, with all of the remaining symbols or number words falling into place. What these children have learned is the successor function, the fact that one can count to infinity by simply adding one on to the previous number word. Chimpanzees never get this “aha” experience, at least under the training conditions tested.

In sum, nonhuman primates tested under a variety of training conditions are capable of learning many of the key properties of the number system, including one-to-one correspondence, ordinality, and cardinality. When primates represent number, they appear to do so on the basis of mental magnitudes, a system that represents number approximately as a quantity—one that can be operated upon with functions that are isomorphic with addition, subtraction, division, and multiplication. I turn next to a discussion of whether animals—in particular, nonhuman primates— represent number spontaneously in the absence of training, and if so, whether this representation is similar to or different from the representations revealed through training.

Number Representation in Animals: Extracting the Spontaneously Available Substrate

The work previously reviewed suggests that under a variety of training regimes, animals have the capacity to acquire some of the core principles underlying numerical computation and representation. Because one goal of comparative research is to understand how and why humans and animals diverged and converged with respect to certain cognitive capacities, it is important to assess what capacities come naturally and spontaneously to animals in the absence of training, for it is precisely such spontaneous abilities that seem so extraordinary in our own species.

Hauser, MacNeilage, and Ware (1996) were the first to use the expectancy violation procedure on animals to explore spontaneous numerical representation. Given the uncertainty of using this procedure with animals—especially semi-freeranging rhesus monkeys living on the island of Cayo Santiago, Puerto Rico—a simplified version of Wynn’s (1992) original design was implemented. Specifically, the goal was to capture the logic of this technique (i.e., no training, looking as a measure, differences captured by contrasting consistent and inconsistent physical events), but to simplify the overall procedure. Thus, we used a between-subject design, ran each subject on only a single trial, and used a purple eggplant rather than a Mickey Mouse doll in order to increase the salience of the object.After we located an adult sitting alone and visually isolated from all other group members, we set up a stage. Subjects in Group 1 (possible: 0 + 1 = 1) watched as an experimenter set down an empty stage, introduced an occluder in front of the stage, presented a single eggplant, lowered it behind the occluder, removed the occluder to reveal one eggplant, and then filmed the subject’s response for 10 s. Subjects in Group 2 (possible: 0 + 1 + 1 = 2) watched as an experimenter set down an empty stage, introduced an occluder in front of the stage, presented a single eggplant and lowered it behind the occluder, presented a second eggplant and lowered it behind the occluder, removed the occluder to reveal two eggplants, and then filmed the subject’s response for 10 s. Subjects in Group 3 (impossible: 0 + 1 + 1 = 1) watched as an experimenter set down an empty stage, introduced an occluder in front of the stage, presented a single eggplant and lowered it behind the occluder, presented a second eggplant and lowered it behind the occluder, removed the occluder to reveal one eggplant, and then filmed the subject’s response for 10 s. In parallel with Wynn’s results, subjects looked longer in the impossible outcome than they did in either of the possible outcomes.

Having had success with this simplified version of Wynn’s design, we ran a more comparable design involving two familiarization trials followed by either a possible or impossible outcome. The results were identical to those in the first condition, with a highly significant increase in response (both over the prior familiarization and when contrasted with the other tests) in the impossible test trial, but no change in the two possible test trial outcomes. The same pattern of response was also obtained in a 2 – 1 = 1 versus 2 test.

These first results using the expectancy violation technique showed that at least one nonhuman animal could be tested in the same way as human infants and with highly interpretable and comparable patterns. Four problems remained. First, because rhesus had not yet been tested on a 1 + 1 = 2 versus 3 condition, it was not yet clear whether they expected precisely two objects following a 1 + 1 operation or whether they expected something like two or more objects. Second, although these results suggest that rhesus can spontaneously compute additions and subtractions of small numbers, it is possible that the differences in looking time are due to differences in surface area or volume, as appears to be the case in comparable experiments on human infants. Third—in contrast to the work on human infants and on nonhuman animals trained in an operant task—it is unclear from these studies whether the rhesus monkey’s capacity to compute over a small number of objects generalizes to larger numbers, and if so, whether their capacity to discriminate larger numbers is precise or approximate. Fourth, although the looking time technique is powerful and of considerable use in comparative studies, it fails to reveal whether the subject can act on the knowledge that is revealed by differential looking at possible and impossible events.

Over the past 5 years, our lab has systematically addressed these issues in two nonhuman primate species—rhesus macaques and cotton-top tamarins. First, basing our conclusions on a series of looking time experiments, we have shown that adults of these two species can compute addition and subtraction operations on small numbers of objects. Specifically, when rhesus macaques see a 1 + 1 operation, they expect precisely two objects, as evidenced by the fact that they look longer at outcomes of one and three; tamarins show the same pattern of response when tested in captivity (Hauser & Carey, 1998, in review; Uller, 1997; Uller, Hauser, & Carey, 2001). Further, rhesus monkeys look longer at the unexpected or impossible outcome in the following conditions: 2 + 1 = 2 versus 3, 1 + 1 = 2 versus 1 big one (equal in volume to the two smaller objects), and 3 –  1 = 2 versus 3. They fail, however, on 1 + 1 + 1 = 2 versus 3, and 2 + 1 + 1 = 3 versus 4 versus 5. These failures, with multiple updates and numbers larger than three parallel the findings reported previously for infants; I will return to the theoretical implications of these patterns later in this research paper.

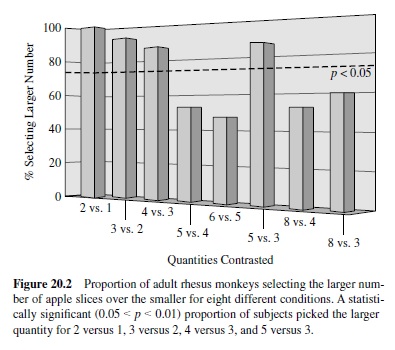
Second, we developed a new technique to explore spontaneous number representation in animals, a procedure that taps into our subjects’natural tendencies to forage and maximize returns. In the first condition (Hauser et al., 2000), we presented semi-free-ranging rhesus monkeys with two empty boxes, placed them on the ground approximately 5 m away from the subject, and then—in sequence—put one piece of apple into one box and a rock into the other. After the experimenter finished loading the boxes, he or she walked away and allowed the subject to approach. Consistently, subjects approached and selected the box with apple. In subsequent conditions, we systematically contrasted different quantities of apple, counterbalancing for the side first loaded and the side with the larger number of apple pieces; for each condition, we ran a total of 15 subjects, and each individual was only tested once. Under these test conditions, subjects selected the box with the larger number of apple slices for two versus one, three versus two, four versus three, and five versus three but showed no preference for five versus four, six versus five, eight versus four, and even eight versus three (Figure 20.2). These results suggest that adult rhesus track the number of objects placed into each box, recall what has been placed in each box, and contrast the quantities before approaching and selecting one box over the other. Given the pattern of results, the capacity to discriminate appears limited to quantities less than four, with no detectable ratio effects. In other words, if our search task tapped a magnitude system that was subject to Weber’s law, then given success on two versus one, subjects should have been successful on eight versus four. Thus, rhesus monkeys appear to be capable of spontaneous and precise small number quantification.

In our search task, the number of apple pieces placed into each box is confounded by time, as well as by volume or surface area. Thus, for example, subjects could pick the box with more apple slices not because they were tracking the number of pieces, but because they were timing the duration of apple-placing events; similarly, they could use the overall volume or surface area to assess which box has more applestuff. To control for time, we ran a second experiment in which we held constant the number of objects going into each box but manipulated the kind of objects going in. Specifically, we placed N apple slices into Box 1 versus N1 apple slices and a rock into Box 2. Although the time required to place objects into each of the two boxes was the same, subjects consistently picked the box with more apple slices, following the same patterns as in the first experiment. As an initial attempt to control for volume, we also ran a condition contrasting half an apple with three pieces of apple equal in volume to the half piece. Here, subjects picked three pieces over one, suggesting that number rather than volume is primary.

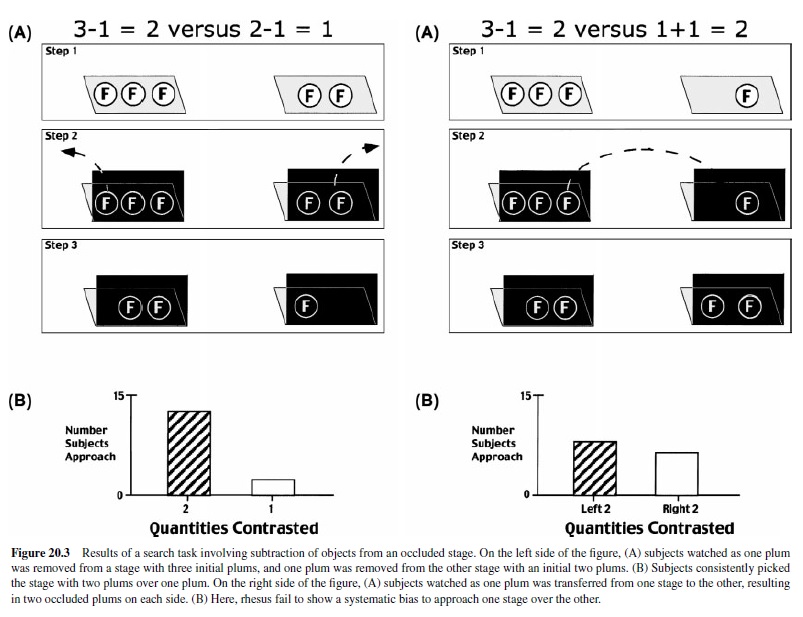
To determine whether the capacity to compute simple additions translates to other mathematical operations, we ran a comparable set of experiments with subtraction (Sulkowski & Hauser, 2001). The only difference in our protocol was that we first presented different quantities of objects (plums) on two physically separated stages, occluded the objects with freestanding occluders, reached behind the occluders, and then removed or added objects. Results showed that rhesus monkeys correctly computed the outcome of subtraction events involving three or fewer objects on each stage, even when the identity of the objects was different. Specifically, when presented with two food quantities, rhesus selected the larger quantity following subtractions of one piece of food from two or three; this preference was maintained when subjects were required to distinguish food from nonfood subtractions and when food was subtracted from either one or both initial quantities (Figure 20.3, top). Furthermore, rhesus monkeys were able to represent zero as well as equality (Figure 20.3, bottom) when two identical quantities were contrasted. We have yet to determine—using the search technique—whether rhesus monkeys can subtract larger quantities of objects and whether they are attending to number or volume as demonstrated in the addition experiments.

In summary, we have demonstrated, using two different methods (looking time and search) on two nonhuman primate species (cotton-top tamarins and rhesus monkeys) under two testing conditions (laboratory-housed, semi-free-ranging), that at least some nonhuman primates spontaneously represent number.All of the results suggest that there is a limit on spontaneous number discrimination on the order of three to four. These data suggest, in parallel with comparable tests of human infants, that in the absence of training, pre- and nonlinguistic animals have a precise, small number system. Under different testing conditions, such as those evidenced by Xu and Spelke’s (2000) work on infants and Brannon and Terrace’s (1998) work on rhesus, subjects tap an approximate, large number system. In the next section, I return to the distinction between small and large numbers and examine the ontogenetic path fromthesetwosystemstoapreciselargenumbersystem—one that is liberated from the constraints of Weber’s law.

Different Number Systems? Insights From Evolutionary Biology, Developmental Psychology, and Cognitive Neuroscience

My goal thus far has been to review what is known about number representation in nonlinguistic creatures—especially nonhuman and human primates. Studies of human infants less than a year of age provide evidence that under certain testing conditions, subjects readily and precisely discriminate small numbers of objects, usually in the range of three to four, and according to at least one study are capable of discriminating two actions (puppet jumps) from three; in some of these studies, infants appear to be paying greater attention to continuous variables such as volume, surface area, or contour, than to the number of discrete objects. In those studies showing sensitivity to small numbers, results suggest that it is in fact discrete number rather than ratios given that they discriminate between one and two but not between 3 and 6 or 5 and 10. However, these data stand in contrast to results showing that when all possible confounding factors are carefully controlled, infants readily discriminate 8 from 16 but not 8 from 12. Thus, at least under some circumstances, infants can discriminate large numbers approximately, and their discrimination appears to be based on Weber’s law.

Studies of nonhuman primates—together with experiments on rats and pigeons—suggest that nonlinguistic animals can be trained to discriminate large numbers approximately, can spontaneously represent small numbers precisely, and with training on Arabic numerals can learn the integer count list from 0–10. Due to the small number of nonhuman primate species tested and the wide range of methodological techniques employed, we are not yet in the position to say whether some species are more proficient on tasks of number discrimination than others. Nonetheless, the patterns emerging from nonhuman primates fit nicely with those emerging from human infants. When spontaneous methods are used, both species show evidence of precise small number discrimination and large approximate number discrimination. It is interesting that in both cases in which large approximate discrimination has been demonstrated (Brannon & Terrace, 1998, 2000; Xu & Spelke, 2000), the task involves visual stimuli that can be directly perceived, and with no memory load. In contrast, in cases in which precise small number discrimination has been demonstrated (Feigenson et al., 2002; Hauser et al., 2000; Hauser et al., 1996), the quantities to be contrasted disappear out of sight and must be evaluated as a set of stored representations. How can we account for the patterns of variation, and in what sense is it reasonable to claim that the abilities of nonlinguistic creatures—both human and nonhuman primates— represent the biological foundations of our culturally elaborated number sense?

At present, two models dominate the literature on number representation (Carey, in press; Dehaene, 1997; Dehaene, 2000; Gallistel, 1990; Gallistel & Gelman, 2000). Some argue that one model is necessary and sufficient, whereas others argue that both are necessary and sufficient. The first model can be traced to the early literature on number discrimination in laboratory animals, which—as has been pointed out here—was closely coupled with studies of timing. Specifically, Meck and Church (1983) suggested that animals represent number as mental magnitudes with scalar variability; recall the pattern of results from Mechner (1958) and Platt and Johnson (1971) in which subjects showed that as the target number of presses increased, so did the mean and variance of the subject’s actual presses. To account for these patterns and the representations presumed to underlie them, Meck and Church proposed an accumulator mechanism whereby each object or event is enumerated or represented as an impulse of activation from the nervous system. To extract number (or time), the accumulator stores each impulse until the end of counting (or timing), and then transfers this information into memory, where it outputs one value for the impulses counted. This process or system can be schematically represented as a growing number line:

• _
• __
• ___
• ____
• · ·

8  ________

Because of variability or noise in the remembered magnitude, the output from the accumulator is an approximation of number, with variability increasing in proportion to magnitude, or what is referred to as scalar variability (Church & Boradbent, 1990; Gibbon, 1977; Gibbon et al., 1997; Roberts, 2000; Whalen, Gallistel, & Gelman, 1999). As Gallistel and Gelman (2000) have recently articulated, under the accumulator model “numerosity is never represented exactly in the nonverbal or preverbal mind, with the possible exception of the first three or four numerosities” (p. 60). Nonetheless, there are at least two advantages of the accumulator model as a mechanism of nonlinguistic number representation. First, it generates a representational format—mental magnitudes with scalar variability—that can be operated over by such arithmetic operations as addition, subtraction, multiplication, and division. Second, it takes as input signals from any sensory modality, and as such, is abstract as demanded by mathematics (e.g., a counting system should be able to enumerate bursts of sound, discrete objects, or actions).

The second model (Carey & Spelke, in press; Hauser & Carey, 1998; Hauser et al., 2000; Simon, 1997) is based on the idea that number—especially small numbers less than about four—may be represented by a system that is used by adults for object-based attention and tracking (Kahneman, 1992; Scholl & Pylyshyn, 1999; Trick, 1994). The basic idea is as follows: When we see an object, we pick it out from the background, using metaphorical fingers of attention to track its movements. For each object, a file is opened and tagged. Based on psychophysical studies of humans, the number of objects (files) that can be simultaneously tracked (opened) is small, on the order of three to five. Thus, for example, in the looking time study involving 1 + 1 = 2, rhesus monkeys watched as one eggplant was placed on stage, occluded, and then a second eggplant was added behind the screen before the outcome was revealed. In this case, one object file is opened for the first eggplant, followed by an updating of this representation and the opening of a second object file when the second eggplant is added. Next, when the occluder is removed, the number of eggplants revealed either matches or mismatches the number of eggplants that were concealed or the number of object files that were opened. In the original model, the system that opens a file does not register what the object is or what features are associated with it. It simply provides a mechanism for object tracking. More recently, however, experiments by Blaser, Pylyshyn, and Holcombe (2000) indicate that humans can track the changing features of an object that is static in one place; as such, humans can track the object as it moves through a feature space. This shows in theory that the object file mechanism is sensitive to both locational and featural cues.

Under the object file model, although there is no explicit representation of number, there is a mechanism capable of providing at least four criteria for constructing numerical representations (Carey & Spelke, in press). First, by using spatiotemporal information, object files are opened based on principles of individuation and numerical identity. Specifically, only entities with clearly articulated object properties (e.g., bounded, moves in a continuous spatiotemporal path) can be enumerated, and each one of these entities is uniquely specified by a set of spatiotemporal coordinates. Second, if one or more object files are opened, opening a new one provides a mechanism for adding one item to an array of items— an operation that is likely to be important for the successor function that is crucial to the integer count list. Third, object files are based on one-to-one correspondence (one file opened for each object, up to a limit of approximately four) and thus may contribute to the establishment of numerical equivalence. Fourth, although the number of object files that can be simultaneously opened is limited, it is precise and not subject to Weber’s law (distance and magnitude effects).

The advantages of each of the models are at least partially offset by disadvantages—both in explaining the existing patterns of results on human and nonhuman animals and in accounting for how human children (at least) acquire a mapping from these initial representational formats (mental magnitudes or object files) to what ultimately becomes a sophisticated understanding of mathematics. One way to reconcile the pattern of results observed, as well as current debates in the literature that pit one model against the other, is to defend a two-model approach—one that views the biological foundations of our number system as depending upon a precise small number mechanism and an approximate large number mechanism. This is precisely the tact that Carey and Spelke (in press) have recently adopted.

Consider once again the work on nonhuman primates and human infants. If number is strictly represented as a mental magnitude, then it is not possible to account for the fact that human infants successfully discriminate two from three dots, but fail to discriminate four from six and 8 from 12 dots (Starkey & Cooper, 1980; Starkey et al., 1990; Xu & Spelke, 2000); the same holds for the observation that rhesus monkeys selectively choose three pieces of apple over two but not eight over four (Hauser et al., 2000). If human infants and rhesus monkeys only tapped a magnitude representation of number, in which Weber’s law holds (i.e., the discriminability of two perceived magnitudes is determined by the ratio of objective magnitudes), then these values should be discriminable because they differ by the same ratio. On the other hand, a magnitude system can account for the fact that human infants are able to discriminate 8 from 16 dots, and rhesus monkeys can discriminate numbers between one and nine, but with a significant decrease in performance as a function of the distance and magnitude of the specific numerical pairings (i.e., one vs. two is easier than seven vs. eight but harder than one vs. four). These results—and the numerical values on which they are based—well exceed the presumed limits of an object file representation. Putting these findings together leads to the suggestion that there might be two relevant systems, one (the object file mechanism) handling small numbers with precision and the other (the accumulator mechanism) handling large numbers approximately.

At present, the two-mechanisms account provides the best explanation for what has been observed in studies of number discrimination among human and nonhuman primates. However, I do not believe that either mechanism—alone or combined—satisfactorily handles the current patterns of variation. To clarify, consider the object file model for precise, small-number discrimination. This model was originally formulated to account for visual object tracking and yet is currently being used to account for an abstract concept such as number, which—by definition—must be able to handle any format of input. As some of the studies previously reviewed suggest, there is evidence for numerical discrimination of sounds and actions. Consequently, in order for the object file mechanism to work in the case of number, one would have to broaden its scope, allowing files to be opened independently of input. This is possible, of course, but we can no longer be confident that the kinds of constraints that have been documented for visual object tracking hold for sounds, actions, or some combination of input formats (see Cowan, 2001, for a possible solution); it is also possible that the object file mechanism works for visual objects and that some other mechanism is recruited for other modalities. Further, although Carey and Spelke (in press) are correct in stating that an object file mechanism sets up critical criteria for number representation, it is not at all clear how such criteria can ultimately service or map onto a fully mature system of mathematics and the representations required. For example, although the opening of files is at some level similar to the successor function, it is clearly not the function because by definition, functions are not constrained or limited to a finite set; they are open-ended. A final limitation of the object file mechanism is that it cannot account for the pattern observed in the twochoice box test run on rhesus monkeys. In this task, the total number of objects tracked well exceeds the presumed limits of this mechanism—that is, rhesus monkeys successfully discriminated four pieces of apple in one box from three in the other, for a total of seven pieces of apple. Moreover, the object file model was not developed to handle operations within each file—a move that is required to handle the sequential updating of objects placed within each box. These problems do not necessarily invalidate the general notion of an object file mechanism for small number discrimination, but they do suggest that the details of the model must be changed, and checked by both behavioral and neurobiological investigations; I turn to these shortly.

Although the accumulator model solves many of the problems associated with the object file mechanism (e.g., no difficulties with varied inputs, multiple accumulators, large numbers, and abstract mathematical functions), it cannot account for precise number discrimination within the range explored, and has difficulty explaining how the developing child generates the appropriate mapping between an approximate number system and a precise one. Some, such as Gallistel and Gelman (2000), have argued that the evidence for small number discrimination in human infants and nonhuman primates is actually not numerical at all. Rather, what appears to be a numerical discrimination is actually just the by-product of the object tracking system. Their main argument here is that this system simply fails to generate the kind of representational format that can be operated over in terms of the basic operations of arithmetic. Although this debate has yet to be resolved, at least some evidence from rhesus monkeys suggests that they are capable of operations that appear isomorphic with addition and subtraction of small numbers (Hauser et al., 2000; Sulkowski & Hauser, 2001). The second point is that if humans come equipped with a mental magnitude system, then the mapping between magnitudes and integers should be relatively straightforward. And yet, work on the child’s acquisition of a count system suggest that it is anything but straightforward. Studies by Wynn (1998) have shown that children under the age of 3 years have acquired the number words but have little understanding of their meaning. Thus, they may count “one, two, three, four. . .” but not know that two means precisely two things, and that after counting the number of cookies on a plate, the last number in the count list represents the total number or the cardinal value. In fact, it is not until the age of approximately 3.5 years that the child grasps the integer count list, with a full appreciation of the successor function and a precise understanding of the meaning of small and large numbers.

The difficulties articulated with each of the models must not be underestimated. At present, however, there are no easy solutions. There are, nonetheless, some interesting directions for future work in this area, involving both additional studies at the behavioral level as well as new studies at the neural level. To conclude, I briefly discuss two such exciting directions. Carey and Spelke (in press) have argued that a key to understanding how an organism develops or evolves from the biological primitives of our number system—small precise and large approximate—to the full-blown, mature system is to explore how language adds on a new and crucial cognitive resource that permits the mapping between systems. Thus, the strong form of Carey and Spelke’s claim is that in the absence of language, the organism will never develop a precise, large number system and consequently will never acquire what all humans with language acquire in the absence of formal schooling. Evidence in favor of this position comes from looking at human-reared chimpanzees who have been taught the Arabic numerals. Although their abilities are impressive, none of these animals have ever generalized beyond the original training set, and their capacity for discrimination appears tied to a mental magnitude representation. There are, however, two critical tests that have yet to be conducted with such animals. First, if Carey and Spelke are correct, the only way to get a proper mapping between the biologically primitive system and the fully developed human adult system is to acquire an arbitrary list of tokens, as appears to occur in all human children. Thus, before human children understand the count list (one-to-one correspondence, ordinality, cardinality), they spout the words in the count list. With this list in place, they can then tap into the biologically primitive system; how this connection is actually forged is still unclear. One would therefore predict that if chimpanzees are first taught the arbitrary count list and then taught the mapping between Arabic numerals and quantities, they should be able to generalize to larger numbers spontaneously, as do human children. A second possible test of this hypothesis involves apes that have had some level of language training. None of the chimpanzees tested thus far on number representation have had any formal training in a natural language. If one grants some level of linguistic ability to these animals (see next section), one can ask whether such additional resources help in acquiring the kind of number representation that we have.

A second approach to understanding both the similarities and differences in number representation across species and age groups comes from recent studies of the underlying neural mechanisms (Butterworth, 1999; Dehaene, 1997, 2000). Neuropsychological studies of patients suggests that deficits in number processing are dissociated from deficits in language processing, and that the deficit is abstract (i.e., computational problems arise for both visually and auditorily presented numbers). For example, some patients can tell you which letter falls between B and D but cannot tell you which number falls between two and four; others have problems reading number words but not nonnumber words. Combined with recent neuroimaging studies, it has been suggested that the intraparietal cortex is selectively involved in approximate number computations, whereas the prefrontal cortex (especially the left hemisphere) is selectively involved in exact number computation. This work stands in contrast to studies of rats indicating that the most likely locus for approximate number (and timing) computation is in the basal ganglia and cerebellum. In order to make headway on the neural basis of number representation, there are several obvious studies. First, if nonhuman animals lack a precise large number system, then during computations of large numbers, there should be no activation of prefrontal cortices and dominant activation of intraparietal cortex. Second, for subjects with explicit training on Arabic numerals as well as language, one might expect to see some activation of prefrontal regions. Third, given the abundant evidence that timing mechanisms are guided by circuits in the basal ganglia and cerebellum, it is essential that future studies of number in animals and humans focus in on these areas. For example, although Parkinson’s patients show impairments on timing discriminations, we do not know whether they show comparable deficits for number or whether administration of dopamine-based medication would alter such deficits. Furthermore, given the capacity to carry out fMRI and positron-emission tomography (PET) studies with nonhuman animals (Logothetis & Sheinberg, 1996; Rolls, 2000), it is possible to explore how a nonlinguistic brain represents number and whether this neural machinery is the same as in humans, both young and old. Such studies of anatomical localization will enable us to determine whether the observed similarities between nonhuman primates and human infants are instances of homology or homoplasy.

Language and the Speech Is Special Debate

“Seen our way, speech perception takes place in a specialized phonetic mode, different from the generally auditory mode and served, accordingly, by a different neurobiology.” (Liberman & Mattingly, 1988, p. 775)

Introduction to the Debate

In a recent lecture at MIT(Massachusetts Institute ofTechnology) entitled “Language and the Brain,” Noam Chomsky spent a substantial proportion of time discussing why the comparative approach to the study of human language (Hauser, 1996)—especially the use of evolutionary theory (Pinker & Bloom, 1990)—has yet to inform our understanding of language, including why it has its own particular design features, is present in all humans, exhibits a characteristic pattern of development, and is grounded by a suite of formal parameters or constraints. This critical position is not a dismissal of the comparative method or of evolutionary theory. Rather, it represents a challenge to evolutionarily oriented scientists to find evidence—one way or the other—that will help us understand the design of language. In one sense, this challenge is no different from any other in the study of comparative biology, including such superb examples as the evolution of the vertebrate eye, avian wing, and primate hand. In this section, I take on Chomsky’s challenge by discussing a research program that I believe has great promise—perhaps more so than do other approaches to the problem of language evolution. In particular, the approach I advocate here represents a return to the classic speech-is-special debate— especially an exploration of the mechanisms that mediate the acquisition of spoken language (for an extensive review, see Trout, 2000). This approach is, in a nutshell, as follows: To establish the unique design features of human language, one must first describe the landscape of mechanisms—both necessary and sufficient—for an organism to acquire language. Next, one must assess how such mechanisms constrain the form of learnable languages. If one establishes that some of these mechanisms are shared with other organisms, then it cannot be the case that such mechanisms evolved for language; rather, they must have evolved for other computational problems and then, during human evolution, were co-opted for language processing. Although there are problems associated with this approach (see the following discussion), by systematically examining a suite of mechanisms employed by humans (both young and old) to acquire language and checking to see which ones are absent among nonhuman animals, we will be in a strong position to specify those mechanisms that evolved specifically for language and that are part of our unique endowment, or what Chomsky has referred to as the faculty of language.

As a brief illustration of this approach, its logic, and its potential pitfalls, consider our system of speech production. Although on a coarse-grained level we share with other mammals a comparable vocal tract, no other mammal produces speech—either the content or the actual sounds—and none of our nearest living relatives (apes and monkeys) have the capacity to imitate sounds. This comparative claim is either trivially true or of considerable interest. To show how it is trivially true, consider the following parallel comment: No other animal except bats and dolphins produces biosonar sounds. To turn this into an interesting comparative claim, one must show how the target mechanism mediates the particular function, and how in the absence of such a mechanism there can be no system with a comparable function. Returning to speech production, if you accept the motor theory (Liberman & Mattingly, 1985)—that the phonetic mode entails the perception of gestures, not sounds—then animals should not have a phonetic mode because surely they do not perceive human gestures. They could, however, perceive the species-typical gestures for making their own species-typical sounds, but because their vocal tract is in fact different (Fitch, 2000), the percept should be fundamentally different as well. So, either this is true (it could be true even if the motor theory is wrong) or it is false (that is, animals perceive speech in a way that is similar to that of humans, in which case the motor theory must be wrong). If it is false, then the perceptual system has undergone little evolutionary change. Going one step further, if we find differences in perception among species, then we need to ask why there are specific perceptual mechanisms that we have that animals lack, and vice versa. Is it because the production system dragged our perceptual system along, or did the perception system open up a new range of possible sounds? Is it because we experienced a perceptual problem in our past that required a new mechanism, but the evolutionary pressure is not one linked to speech? These are all possibilities, and a comparative approach to language evolution must address them.

Before turning to some of the relevant empirical work, let me briefly mention three other comparative approaches to the study of language evolution that I believe have met with mixed success, at least with respect to current reception by linguists and psycholinguists. The first, pioneered by Lieberman (1968, 1984; Lieberman, Klatt, & Wilson, 1969) over 30 years ago, involves exploration into the mechanisms of speech production. In contrast to all other animals, the position of the larynx is substantially lower in modern humans. This anatomical difference, together with the accompanying changes in the supralaryngeal vocal tract (e.g., two-plus tube, bent at a 90° angle, permitting resonances in both the nasal and oropharyngeal cavities) and neural circuitry for motor control, have led to the capacity to generate a far richer array of formant frequencies. This enhanced frequency range is relevant to the evolution of language, so the argument goes, because there would have been strong selection on humans to evolve an efficient acoustic vehicle for conveying information about complex ideas. Although current work on this topic—especially by Fitch (2000)—shows that many of the adaptations for vocal production seen in humans are not unique, it is clear that work on vocal production has not yet illuminated those problems that are of deepest concern to linguists. In exploring the literature, it appears that only a small circle of linguists—mostly those working on phonology (MacNeilage, 1998; Studdert-Kennedy, 1998)—have been at all influenced by the comparative data.

The second approach—also started over 30 years ago— focuses on whether nonhuman animals have the potential to acquire a human language (Gardner & Gardner, 1969; Herman & Uyeyama, 1999; Pepperberg, 2000; Premack, 1986; Savage-Rumbaugh, 1986; Savage-Rumbaugh et al., 1993). More than any other approach, this work has certainly captured the attention of linguists (for a critical review, see Wallman, 1992), although the level of impact has been mixed and highly variable over the years. In general, there have been two areas of concern or debate: One, what does it mean to show that an ape’s brain has the potential to acquire some aspects of human language, although such characteristics are not employed in their own communicative systems? Two, to what extent is the proclaimed capacity of some animals to signal symbolically and to combine symbols into new expressions truly like the human capacity to use words and to form sentences? At present, I do not think that there is a satisfactory answer to the first question. Even if we accept only a limited capacity for symbolic signaling and syntactic constructions in human-trained animals (Deacon, 1997), it is not at all clear why an animal with such potential would not employ its capacities when communicating with others of its kind. As is pointed out later in this research paper, the natural repertoires of animals fail to show anything like the capacity of human-reared individuals to produce or comprehend referential signals that can be recombined into new expressions; even more surprising, the best evidence for a symbolic system in the natural repertoires of animals has come from studies of monkeys, not apes! As for the second question, the jury is still out, but new data coming in from Savage-Rumbaugh’s lab in particular will have to be treated critically but fairly by linguists; if there is to be a science that includes languagetrained animals, then linguists must work with comparative psychologists so that reasonable standards can be set and explored.

A third approach stems from classical ethology and focuses on the natural communication of animals. These studies, conducted primarily in the wild, have asked whether animals can produce signals that refer to objects and events in the external environment, and whether they can combine these signals to create utterances with a potentially infinite range of possible meanings. Since the pioneering work on vervet monkey alarm calls (Marler, 1978; Seyfarth, Cheney, & Marler, 1980a, 1980b; Struhsaker, 1967), which implied a relatively primitive system of referential signals, there have been several other studies showing that this capacity is present in other species (several old-world monkeys and domestic chickens) and can be extended to other contexts outside of predator-prey interactions (Cheney & Seyfarth, 1988, 1990; Dittus, 1984; Evans & Marler, 1995; Fischer, 1998; Gouzoules, Gouzoules, & Marler, 1984; Hauser, 1998; Marler, Dufty, & Pickert, 1986; Zuberbuhler, Cheney, & Seyfarth, 1999; Zuberbuhler, Noe, & Seyfarth, 1997). Furthermore, some studies have suggested that animals can recombine discrete elements of their repertoire to produce new signals (Cleveland & Snowdon, 1981; Hailman & Ficken, 1987; Robinson, 1979, 1982). Although some linguists have discussed this work (Bickerton, 1990; Pinker, 1994), it has generally made no impact on how linguists think about the problem of reference or syntax (for a recent review, see Jackendoff, 1999). I believe there is a simple reason for this. In terms of reference, the apparent capacity in animals is so fundamentally different from that in humans that it is not at all clear whether one should think about the calls of some birds and primates as precursors to our words or as something completely different and disconnected from the evolutionary path to human referential signals. For example, although vervet and diana monkey alarm calls may in fact stand for a particular predator and thus function like a label in our natural languages, the underlying capacity for generating referential signals is highly impoverished relative to even a 1-year-old child. The signals of animals are restricted to the present (i.e., they do not provide information about past events or future encounters) and can be entirely predicted by current context (i.e., if you know what the animal has recently experienced, you can predict what vocalization it will produce, if it produces one at all). Moreover, the system appears closed, with no evidence that animals can create new utterances designed to meet new situations; this stands in contrast to the evidence that animals—especially chimpanzees—have the capacity to solve novel ecological and social problems in new ways, inventing new tools or new strategies for overthrowing a competitor (Hauser, 2000; Whiten et al., 1999). Similarly, of the studies exploring the possibility of syntactic constructions, there is no evidence that combination signals have anything like new meaning; rather, when animals appear to combine discrete signals into new strings, the only detectable change appears to be associated with the caller’s affective state; in the case of songbirds, in which the evidence for rule-guided changes in structure is most apparent, syllable arrangement plays no role in meaning or function; rather, it conveys information about species, sex, and individual identity—and in some cases, reproductive potential.

The Speech Is Special Debate: Some History

In the 1960s, Liberman and his colleagues at the Haskins lab (Liberman, Cooper, Shankweiler, & Studdert-Kennedy, 1967; Liberman, Delattre, & Cooper, 1958; Liberman, Harris, Hoffman, & Griffith, 1957) began to explore in detail the mechanisms underlying human speech perception. What is interesting about the claims emerging from Haskins at this time is that they were intellectually allied with Chomsky’s (1957, 1965, 1966) position concerning the special nature of human language. In particular, it is clear that Chomsky thought of the language organ as uniquely human and that its capacity for generating syntactical structure evolved for reasons that had nothing to do with communication (Chomsky, 1988). Although one can certainly challenge this claim, what is important for biologists about Chomsky’s position is that it sets up a testable hypothesis about the nature of the comparative database (Hauser, 1996). Specifically, if humans are truly unique with respect to the language organ, then we should see little to no evidence of precursor mechanisms in other animals. This brings us back to Liberman and the Haskins lab. In particular, much of the early work on speech perception was aimed at identifying particular signatures of an underlying, specialized mechanism. Perhaps one of the most important and early entries into this problem was Liberman’s discovery of the phenomenon of categorical perception; note that for Chomsky, data on perceptual mechanisms are only of interest in so far as they interface with and constrain core computational mechanisms that are central to the faculty of language.

Categorical Perception of Speech and Species-Typical Vocalizations

When we perceive speech, we clearly create categories. Using an artificially created acoustic continuum running from /ba/ to /pa/, human adults show excellent discrimination of between-category exemplars and poor discrimination of within-category exemplars. To determine whether the mechanism underlying categorical perception is specialized for speech, uniquely human, and fine-tuned by the linguistic environment, new methods were required, as were subjects other than human adults. In response to this demand, the phenomenon of categorical perception was soon explored in (a) adult humans using nonspeech acoustic signals as well as visual signals, (b) human infants using a habituation procedure with the presentation of speech stimuli, and (c) animals using operant techniques and the precise speech stimuli used to first demonstrate the phenomenon in adult humans (Harnad, 1987). Results showed that categorical perception could be demonstrated for nonspeech stimuli in adults (Bornstein, 1987; Remez, Rubin, Pisoni, & Carrell, 1981) and for speech stimuli in both human infants (Eimas, Siqueland, Jusczyk, & Vigorito, 1971) and nonhuman animals (Kuhl & Miller, 1975; Kuhl & Padden, 1982, 1983). Although the earliest work on animals was restricted to mammals (i.e., chinchillas, macaques), more recent studies have provided comparable evidence in birds (Dent, Brittan-Powell, Dooling, & Pierce, 1997; Kluender, Diehl, & Killeen, 1987); this suggests that the mechanism underlying categorical perception in humans may be shared with other animals and may have evolved at least as far back as the divergence point with birds.

The parallel results on humans and animals raise at least two important points. First, although this finding does not rule out the importance of categorical perception in speech processing, it does suggest that the underlying mechanism is unlikely to have evolved for speech. In other words, the capacity to treat an acoustic continuum as comprised of discrete acoustic categories is a general auditory mechanism that evolved before humans were producing the sounds of speech. Second, although the behavior associated with classifying exemplars into discrete categories is similar to what has been observed in humans, we must move cautiously in assuming that the underlying mechanism is precisely the same. Specifically, studies of categorical perception in animals and humans employ different techniques. Animals are trained to respond to particular categories and then are tested for spontaneous generalization. In contrast, tests of humans involve spontaneous classification and are also explicitly influenced by instructions. Thus, for example, in the elegant experiments on sine wave speech by Remez, human listeners show patterns of classification if they are informed that they will be listening to speech stimuli different from patterns they show if they are not told about the nature of the stimuli. Thus, although animals clearly classify an acoustic continuum into discrete categories and show the same kinds of boundary effects as do humans, they may in fact be using quite different mechanisms in processing such stimuli.

Emphasizing the point that categorical perception—at least the behavioral phenomenon—most likely evolved prior to the evolution of speech are experiments involving the presentation of species-typical vocalizations, as opposed to speech (reviewed in Hauser, 1996; Kuhl, 1989; Wyttenbach & Hoy, 1999). And here, the breadth of species tested is extraordinary, including field crickets (Wyttenbach, May, & Hoy, 1996), swamp sparrows (Nelson & Marler, 1989), mice (Ehret & Haack, 1981), pygmy marmosets (Snowdon, 1987), and Japanese macaques (May, Moody, & Stebbins, 1989). One of the best examples—based on methodological elegance as well as functional and ecological considerations— comes from Wyttenbach and Hoy’s work on the field cricket. In this species, individuals produce a contact call of 4–5 kHz. When conspecifics hear this call, they often approach. In contrast, predatory bats produce ultrasonic signals in the 25–80 kHz range, and when crickets hear such sounds, they move away. The perceptual task therefore involves a discrimination between two ecologically meaningful acoustic signals—one that elicits approach and a second that elicits avoidance. Laboratory experiments had already indicated a transition between approach and avoidance in the 10–20 kHz range. In the labeling task, crickets were presented with signals that varied from 2.5–40 kHz. Results showed an abrupt transition from approach to avoid between 13–16 kHz, providing strong evidence of a categorical boundary. In the discrimination task, crickets were habituated to 20 kHz pulses (i.e., a signal that elicits escape), and a photocell was used to measure the movement of the subject’s hind leg. After subjects habituated (i.e., showed little to no escape response), they then received one test stimulus from a different frequency and one 20 kHz stimulus. Of the frequencies tested, only stimuli falling below 16 kHz caused dishabituation; no stimuli falling in the ultrasound range caused dishabituation, providing strong evidence of between-category discrimination.

Beyond Categorical Perception

The history of work on categorical perception provides an elegant example of the comparative method. If you want to know whether a mechanism has evolved specifically for a particular function in a particular species, then the only way to address this question is by running experiments on a broad array of species. With respect to categorical perception, at least, it appears that the underlying mechanism did not evolve for processing speech. To repeat, because of differences in methods, and the lack of neurophysiological work, we can not be absolutely confident that the underlying mechanisms are exactly the same across species even though the classificatory results are the same. Nonetheless, a question arises from such work: What, if anything, is special about speech, especially with respect to processing mechanisms? Until the early 1990s, scientists studying animals pursued this problem, focusing on different phonemic contrasts as well as formant perception (Lotto, Kluender, & Holt, 1998; Sinnott, 1989; Sinnott & Brown, 1997; Sinnott, Petersen, & Hopp, 1985; Sommers, Moody, Prosen, & Stebbins, 1992); most of this work suggested common mechanisms shared by humans and nonhuman primates. In the early 1990s, however, Patricia (Kuhl 1991; Kuhl, Williams, Lacerda, Stevens, & Lindblom, 1992) published two papers showing that human adults and infants but not rhesus monkeys perceive a distinction between so-called good and bad exemplars of a phonemic class. The good exemplars, or prototypes, functioned like perceptual magnets, anchoring the category and making it more difficult to distinguish the prototype from sounds that are acoustically similar; nonprototypes function in a different way and are readily distinguished from more prototypical exemplars. In the same way that robins and sparrows but not penguins or storks are prototypical birds because they carry the most common or salient visual features (e.g., feathers, beak, wings) within the category bird, prototypical phonemes consist of the most common or salient acoustical features. Although there is controversy in the literature concerning the validity of this work in thinking about the perceptual organization and development of speech (Kluender, Lotto, Holt, & Bloedel, 1998; Lotto et al., 1998), my concern here is with the comparative claim. Because Kuhl failed to find evidence that rhesus monkeys distinguish prototypical from nonprototypical instances of a phonetic category, she argued that the perceptual magnet effect represents a uniquely human mechanism specialized for processing speech. Moreover, because prototypes are formed on the basis of experience with the language environment, Kuhl further argued that each linguistic community will have prototypical exemplars tuned to the particular morphology of their natural language (Kuhl, 2000).

To address the comparative claim, Kluender and colleagues (1998) attempted a replication of Kuhl’s original findings, using European starlings and the English vowels /i/ and /I/, as well as the Swedish vowels /y/ and /u/; these represent the stimuli used in Kuhl’s original work on the prototype effect. Based on a mel scale of the first and second formants, these vowels have distinctive prototypes that are acoustically nonoverlapping. After starlings were trained to respond to exemplars from these vowel categories, they readily generalized to novel exemplars. More important was that the extent to which they classified a novel exemplar as a member of one vowel category or another was almost completely predicted by the first and second for meant frequencies, as well as by the exemplar’s distance from the prototype or centroid of the vowel sound. Because the starlings’ responses were graded and matched human adult listeners’ ratings of goodness for a particular vowel class, Kluender and colleagues conclude—contra Kuhl—that the perceptual magnet effect is not uniquely human and can be better explained by general auditory mechanisms.

In contrast to the extensive comparative work on categorical perception, we have only two studies of the perceptual magnet effect in animals. One study of macaques claims that animals lack such capacities, whereas a second study of starlings claims that animals have such capacities. If starlings perceive vowel prototypes but macaques do not, then this provides evidence of a homoplasy—a character that is similar between species because of convergent evolution. Future work on this problem must focus on whether the failure with macaques is due to methodological issues (e.g., would a different testing procedure provide different results?) or to an absence of a capacity. If macaques lack this capacity and starlings have it, then our evolutionary account must reject the claim concerning uniqueness but attempt to explain why the capacity evolved at least twice—once in the group leading to songbirds and once in the group leading to modern humans; of course, we must also leave open the possibility of a difference in the actual mechanism underlying a perceptual magnet effect in starlings and humans.

What Mechanisms Are Spontaneously Available to Animals for Speech Perception and Language Acquisition?

To date, every time a claim has been made that a particular mechanism X is special to speech, animal studies have generally shown that the claim is false, at least at a general level of behavioral responses. Speech scientists might argue, however, that these studies are based on extensive training regimes, and thus fail to show what animals spontaneously perceive—or more appropriately, how they actually perceive the stimuli. They might also argue that the range of phenomenon explored is narrow and thus fails to capture the essential design features of language (Trout, 2000). In parallel with our work on number (discussed earlier in this research paper), my students and I have been pushing the development of methodological tools that involve no training and can be used with human infants, thereby providing a more direct route to understanding which mechanisms are spontaneously available to animals for processing speech and which are uniquely human. Next, I describe several recent experiments designed to explore which of the many mechanisms employed by human infants and children during language acquisition are spontaneously available to other animals.

As mentioned earlier in this research paper, a powerful technique for exploring spontaneous perceptual distinctions is the habituation-dishabituation technique (Cheney & Seyfarth, 1988; Eimas et al., 1971; Hauser, 1998). Given the variety of conditions in which our animals live, each situation demands a slightly different use of this technique. The logic underlying our use of the procedure for exploring the mechanisms of speech perception is, however, the same. In general, we habituate a subject to different exemplars from within an acoustic class and then present them with a test stimulus. A response is scored if the subject turns and orients in the direction of the speaker. We consider the subject to be habituated if it fails to orient toward the speaker on at least two consecutive trials; as such, all subjects enter the test trial having failed to respond on the previous two trials. The advantage of this approach is that we can not only score whether they respond to the test stimulus, but in some cases we can also score the magnitude of their response—that is, we can score the amount of time spent looking in the direction of the speaker. In the case of speech stimuli, duration is not a reliable measure, whereas in the case of conspecific vocalizations it is.

The first habituation-dishabituation playback experiment on speech perception was run by the collaboration of Franck Ramus, Marc Hauser, Cory Miller, Dylan Morris, and Jacques Mehler (2000). Theoretically, we wanted to understand whether the capacity of human infants to both discriminate and subsequently acquire two natural languages is based on a mechanism that is uniquely human or shared with other species. Although animals clearly lack the capacity to produce most of the sounds of our natural languages, their hearing system is such (at least for most primates; Stebbins, 1983) that they may be able to hear some of the critical acoustic features that distinguish one language from another. To explore this problem, we asked whether French-born human neonates and cotton-top tamarin monkeys can discriminate sentences of Dutch from sentences of Japanese and whether the capacity to discriminate these two languages depends on whether they are played in a forward (i.e., normal) or backwards direction; given the fact that adult humans process backwards speech quite differently from forward speech, we expected to find some differences, although not necessarily in both species. Methodologically, we wanted to determine whether tests of speech processing could be run on neonates and captive cotton-top tamarins using the same stimuli and procedure. Specifically, would tamarins attend to sentences from a natural language, and could we implement the habituation-dishabituation technique to ask questions about discrimination? These methodological questions were significant because all prior work on speech perception in animals involved operant training procedures and relatively short segments of speech (i.e., phonemes or syllables) as opposed to naturally produced sentences.

Neonates and adult tamarins were tested in four different conditions involving naturally produced sentences of Dutch and Japanese. In the first language change condition, we habituated subjects to sentences from one language played in the normal-forward direction and then tested them with sentences from the second language played in the normalforward direction. In the second language change condition, we played all sentences backwards, but with the same shift from one language to the other. In the first speaker change condition—run as a control for the language change condition—we habituated subjects to normal-forward sentences produced by two speakers of one language and then tested them with normal-forward sentences of a language that was the same but spoken by two new speakers. The second speaker change condition was the same but with the sentences played backwards.

There were a few differences in the testing proceduresused for neonates and tamarins. The behavioral assay for neonates was a high-amplitude sucking response, whereas for tamarins we used a head-orienting response in the direction of the concealed speaker. For neonates, we played back habituation stimuli until the sucking response attenuated to 25% less than it was the previous minute; then we maintained this level for 2 consecutive minutes. After subjects were habituated, we played a cycle of test stimuli. For tamarins, in contrast, we played back exemplars from the habituation category until the subject failed to orient on two consecutive trials. Following habituation, we played back sentences of the test category. If subjects failed to respond in the test trial, we played a posttest stimulus—specifically, a tamarin alarm call. The logic behind the posttest was to ensure that the tamarins had not habituated to the entire playback setup.Thus, if they failed to respond in the posttest, we assumed that they had habituated to the setup and reran the entire session a few weeks later.

Neonates failed to discriminate the two languages played forward and also failed to discriminate the two speakers. Rather than run the backwards condition with natural speech, we decided to synthesize the sentences and run the experiment again with new subjects. One explanation for the failure with natural speech was that discrimination was impaired by the significant acoustic variability imposed by the different speakers. Consequently, synthetic speech provides a tool for looking at language discrimination while eliminating speaker variability. When synthetic speech was used, neonates dishabituated in the language change condition, but only if the sentences were played forward; in the backward speech condition, subjects failed to dishabituate.

In contrast to the data on neonates tested with natural speech, tamarins showed evidence of discrimination in the forward, language-change condition but failed to show evidence of discrimination in any of the other conditions (Figure 20.4). When the synthetic stimuli were used, the results were generally the same. Only the forward language-change condition elicited a statistically significant level of discrimination, although the backward speaker change was nearly significant; thus, there was a nonsignificant difference between the language- and speaker-change condition. When the data from the natural and synthetic stimuli were combined, tamarins showed a highly significant discrimination of the forward language-change condition but no other condition.

These results allow us to make five points with respect to studying the speech is special problem. First, the same method can be used with human infants and nonhuman animals. Specifically, the habituation-dishabituation paradigm provides a powerful tool to explore similarities and differences in perceptual mechanisms and avoids the potential problems associated with training. Second, animals such as cotton-top tamarins not only attend to isolated syllables as previously demonstrated in studies of categorical perception, but also attend to strings of continuous speech. Consequently, it is now possible to ask comparative questions about some of the higher order properties of spoken languages, including some of the relevant prosodic or paralinguistic information. Third, given the fact that tamarins discriminate sentences of Dutch from sentences of Japanese in the face of speaker variability, they are clearly able to extract acoustic equivalence classes. This capacity is not present in the human neonate, coming on line a few months after birth (Jusczyk, 1997; Oller, 2000). Fourth, because tamarins fail to discriminate sentences of Dutch from sentences of Japanese when such sentences are played backwards, their capacity to discriminate such sentences when played forward shows that they must be using specific properties of speech as opposed to low-level cues. Fifth, given that the tamarins’capacity to discriminate Dutch from Japanese was weaker in the second test involving synthetic speech, it is possible that newborns and tamarins are responding to somewhat different acoustic cues. In particular, newborns may be more sensitive to prosodic differences (e.g., rhythm), whereas tamarins may be more sensitive to phonetic contrasts. Future research will explore this possibility.

A real-world problem facing the human infant is how to segment the continuous acoustic stream of speech into functional units such as words and phrases. How, more specifically, does the infant know where one word ends and another begins? One might think that such information comes for free, given that there are pauses between words. Such changes in the time-amplitude envelope would provide the relevant cues some of the time but would not provide a reliable mechanism, given that coarticulatory effects create pauses within words as well as continuity in the signal between words. Similarly, although it is clear that adults may help infants pick out words within a sentence, thanks in part to their dramatic emphasis (e.g., Look at the ball!), such stress patterns do not help with all or even most words within a sentence (e.g., no stress cues help with Look, at, and the). A recent attempt to tackle this problem comes from work that follows up on a suggestion from early work in computational linguistics—in particular, the possibility that infants extract words from the acoustic stream by paying attention to the statistical properties of a given language. For example, when we hear the consonant string st, there are many phonemes that we might expect to follow (e.g., ork, ing, ack) but some that we explicitly would not expect (e.g., kro, gni, cak). Saffran, Aslin, and Newport (1996) tested the hypothesis that infants are equipped with mechanisms that enable them to extract the statistical regularities of a particular language. Eight-monthold infants were familiarized for 2 min with a continuous string of synthetically created syllables (e.g., tibudopabikudaropigolatupabiku. . .), with all prosodic and coarticulatory effects removed. Within this continuous acoustic stream, some three-syllable sequences always clustered together (i.e., always had a transitional probability of 1.0 between adjacent syllables—pabiku), whereas other syllables were only sometimes followed by another syllable (e.g., when the syllable pi occurred, it was followed by gola one third of the time, and by daro or tibu the other times). To determine whether infants would extract such statistics, they were presented with three types of test items following familiarization: words consisting of syllables with a transitional probability of 1.0, part words in which the first two syllables had a transitional probability of 1.0 and the third syllable had a transitional probability of 0.33, and nonwords in which the three syllables were never associated (transitional probability of 0.0) in the familiarization corpus. Based on dozens of comparable studies on human infants, Saffran et al. predicted that if the infants have computed the appropriate statistics and extracted the functional words from this artificial language, then they should show little to no orienting response to familiar words but should show interest and an orienting response to both the part words and the nonwords. Results provided strong support for this hypothesis. Although some interpreted this finding as providing evidence against a strong nativist position on language acquisition (i.e., the capacity to compute transitional probabilities is domain-general, not domain-specific) while others argued that these capacities simply cannot do the work required for language acquisition, they undoubtedly show an early capacity to compute conditional statistics. And it is precisely these kinds of computations—together with others—that might help put the child on the path to acquiring a language. Regardless of the outcome of this debate, one can also ask whether the capacity to compute such statistics is uniquely human and—equally important—special to language.

Saffran, Newport, and Aslin have attacked the special to language problem by showing that—at least for transitional probabilities—the same kinds of results hold for melodies, patterns of light, and motor routines (Saffran, Johnson, Aslin, & Newport, 1999). A different approach comes from testing nonhuman animals.

Several studies of pigeons, capuchin monkeys, and rhesus monkeys demonstrate that under operant conditions, individuals can learn to respond to the serial order of a set of approximately 8–10 visual or auditory items (D’Amato & Colombo, 1990; Orlov, Yakoviev, Hochstein, & Zohary, 2000; Terrace, 1993; Terrace, Chen, & Newman, 1995; Wright & Rivera, 1997). These results show that at least some animals—and especially some primates—have the capacity to attend to strings of items, extract the relevant order or relationship between items, and use their memory of prior responses to guide future responses. In addition to these data, observations and experiments on foraging behavior and vocal communication suggest that nonhuman animals also engage in statistical computations. For example, results from optimal foraging experiments indicate that animals calculate rates of return, sometimes using Bayesian statistics, and some animals produce strings of vocalizations such that the function of the signal is determined by the order of elements (Hailman & Ficken, 1987; Hauser, 2000; Stephens & Krebs, 1986). Recently, studies by Savage-Rumbaugh and colleagues (1993) suggest that at least some human-reared bonobos have some comprehension of speech and specifically attend to the order in which words are put together in a spoken utterance; regardless of whether their capacity is considered to be at the level of human adults, these observations suggest that bonobos have the capacity to extract words from a speech stream and at some level appreciate that the order of words within an utterance plays a role in meaning. Together, these studies suggest that like human adults and infants, nonhuman animals may also be equipped with statistical learning mechanisms.

Based on the previously reported evidence, Hauser, Newport, and Aslin (2001) used the original Saffran et al. (1996) material in order to attempt a replication with cottontop tamarin monkeys of the statistical learning effects observed with human infants. The procedure was the same as that used with human infants, with two exceptions. Unlike human infants, who were exposed to the familiarization material for 2 minutes and then presented with the test items (in association with a flashing light), the tamarins were exposed in their home room to 21 min of the familiarization material on Day 1; then on Day 2 we presented individuals located in a soundproof chamber with 1 min of the familiarization material followed by a randomly presented set of test items. We divided our colony into two groups. One group received Version A of the language, whereas the second group received Version B; the transitional probabilities were the same for both languages, but the potential test items differed in terms of their syllabic content. On the first test session, we compared the tamarins’responses to words versus nonwords. On the second session, we compared their response to words and part words. Like the tests on the infants, these tests had several possible outcomes. If tamarins simply respond to novelty as opposed to familiarity, then they might show a significantly higher level of response (i.e., orienting to the concealed speaker) in the word versus nonword condition but fail to show a difference between word and part word; in other words, because the first two syllables are familiar in the partword comparison, while the third is novel, this difference may be insufficient to differentiate the two test items. In contrast, if tamarins compute the transitional probabilities, then nonwords and part words are both novel and should elicit a greater number of responses when contrasted with words. Like human infants, tamarins oriented to playbacks of nonwords and words more often than to words (Figure 20.5). This result is powerful not only because tamarins show the same kind of response as do human infants, but also because the methods and stimuli are largely the same and involve no training.

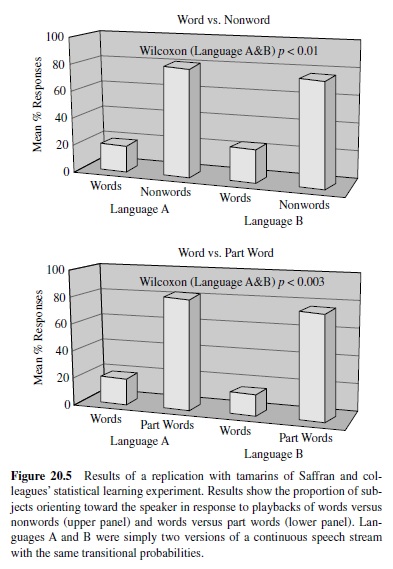
In terms of comparative inferences, our results on statistical learning should be treated somewhat cautiously because of subtle differences in methods between species, the lack of information on where in the brain such statistics are being computed, and the degree to which such computations can operate over any kind of input (i.e., visual, motoric, melodic). Methodologically, the tamarins received far more experience with the familiarization material than did the infants. We provided the tamarins with more input because we were unsure about the time that they would even listen to such synthetic speech, no less orient to it. Nonetheless, future work must establish how much experience is necessary in order to derive the appropriate statistics and how the properties of certain statistics are either learnable or unlearnable by both humans and nonhumans. For example, can human infants and nonhuman animals learn about statistical correlations between nonadjacent elements, and if so, over what kinds of distances? Assuming that human infants or toddlers can compute a different class of statistics than can nonhuman animals, which of these statistics are critically and perhaps uniquely involved in the acquisition of language but no other domain?

Implications for Linguistics and the Neurosciences

What can be said about our verbal abilities? Unique or not? If I had to place a wager, I would bet that humans share with other animals the core mechanisms for speech perception. More precisely, we inherited from animals a suite of perceptual mechanisms for listening to speech—ones that are quite general and did not evolve for processing speech. Whether the similarities across species represent cases of homology or homoplasy cannot be answered at present and will require additional neuroanatomical work, tracing circuitry, and establishing functional connectivity. What is perhaps uniquely human, however, is our capacity to take the units that comprise spoken and signed language and recombine them into an infinite variety of meaningful expressions. Although much work remains, my guess is that animals will lack the capacity for recursion, and their capacity for statistical inference will be restricted to items that are in close temporal proximity. With the ability to run animals and human infants on the same tasks with the same material, we will soon be in a strong position to pinpoint when during evolution and ontogeny we acquired our specially designed system for language.

One direction that is likely to be extremely productive—in contributing to our basic understanding of how human infants acquire a language and how the brain’s plasticity and representational structure change over time—is to use nonhuman animals as models for exploring the specific effects of experience on acoustic processing. One of the major revolutions within the neurosciences over the last 10 or so years has been the discovery that there is plasticity in the adult brain, dictated in part by experience (Kaas, 2000; Recanzone, 2000). This revolution actually started earlier, driven in part by the magnificent findings on some songbird species—their capacity to learn new songs each season, guided by changes in the volume of key nuclei and the shift in levels of circulating testosterone (Alvarez-Buylla, Kirn, & Nottebohm, 1990; Alvarez-Buylla, Theelen, & Nottebohm, 1988; Doupe, Brainard, & Hessler, 2000). More recent work on mammals (mostly rats and some primates) has shown that when an individual engages in repetitive motor routines or is repeatedly presented with sounds falling within a particular frequency range, the relevant cortical representations are dramatically altered (Jenkins, Merzenich, Ochs, Allard, & Guic-Robles, 1990; Kaas, 2000; Kilgard & Merzenich, 1998; Recanzone, 2000). Similar kinds of effects have been suggested in cases of human infants and language acquisition (Kuhl, 2000), as well as patients reporting phantom limb effects (Ramachandran, 1993; Yang et al., 1994).

Given the evidence for cortical plasticity, we are ideally placed to provide our subjects with specific linguistic experience and then test for reorganization of perceptual sensitivity. For example, consider the results on tamarins showing a capacity to distinguish two different languages from two different rhythmic groups (i.e., Dutch and Japanese). Studies of human infants suggest that whereas natives of one rhythmic group (e.g., French) can discriminate sentences of their own language from sentences of another language within the same rhythmic group (e.g., Spanish), infants exposed to a language

Comparative Cognition: The Next Generation

that falls outside this rhythmic group cannot discriminate French from Spanish. To test whether this follows from general auditory principles or from a specialized speech mechanism that is uniquely human, we can passively expose our subjects to sentences from one language over a period of weeks or months and then explore whether such experience influences their capacity to discriminate the so-called native language with other languages, as well as the capacity to make fine-grained discriminations within the exposed language. Similarly, it is possible to selectively expose captive primate infants at different stages of development and thereby determine whether there are critical periods for exposure and their consequences. These results can then be used to fuel studies exploring the neurophysiology underlying behavioral or perceptual changes.

Comparative Cognition: The Next Generation

Comparative studies of animal minds have entered a new era. This shift is due in part to a clearing of earlier conceptual veils—theoretical perspectives that saw animals as mindless, at the base of some intellectual hierarchy, or as mere pawns to be maneuvered for purely biomedical gains. The new era of investigation is based on a marriage between Darwin’s theory of evolution and the representational-computational theory of mind that tends to dominate much of current cognitive science. Underlying or supporting this marriage are a set of methodological tools that have been developed by ethologists, animal learning psychologists, cognitive scientists, neuroscientists, and developmentalists. In this essay, I have attempted to highlight some of the empirical offspring from this new marriage by discussing two problems: the capacity to represent numerosities and the mechanisms recruited to process speech. In the case of number, studies show that a wide variety of animals—primates included—have the ability to discriminate small numbers precisely and large numbers approximately. At present, it appears that over the course of human evolution, we acquired a mechanism that allowed only our species to discriminate large numbers precisely; this capacity ultimately led to our unique gift for complex mathematics. Although it is a currently untested hypothesis, one candidate mechanism is language—in particular, the combinatorial and recursive aspects that underlie our capacity to create an infinite number of meaningful verbal and mathematical expressions. With respect to speech-processing mechanisms, I have argued that we share with other animals all of the core perceptual tools for extracting the salient features of the speech stream. At present, there are no clear-cut mechanisms that we have that no other animal has. But this work is only in its infancy, with many more important processes to investigate from a comparative perspective.

What I have emphasized in this essay is that the future of comparative studies of cognition—especially comparisons between human and nonhuman primates—hangs on three factors. First, to understand loci of convergence and divergence in cognitive capacities, we must develop methods that can be used across species, with little to no modification. I have focused primarily on methods that involve no training because I believe that these are most appropriate for comparative studies of animals and human infants. This focus in no way implies that other methods—especially those involving intensive training—are less important. On the contrary, a complete understanding of cognitive abilities in primates will come from the use of different methods that can be brought to bear on the same set of conceptual problems. Second, studies at the behavioral level must be united with studies at the neural level. Methodologically, this is important because we should use behavioral tasks that are sensitive to the problems that each species evolved to solve. Theoretically, this is important as well because we should use our understanding of the neural mechanisms to refine our assessments of whether similarity at the level of behavior is mediated by similarity at the level of the brain. Because similarity at one level may not be matched by similarity at another, we may end up with different kinds of claims with respect to the distinction between homology and homoplasy. Third, studies of primate cognition are increasingly being used to constrain theoretical arguments in the study of human cognition—in particular, infant cognitive development. In the same way that humans with damage to particular regions of the brain can be used to explore the functional architecture of the human mind, studies of nonhuman primates can be used to test which aspects of the mind are possible in the absence of language. Turning one of David Premack’s famous quotes around, even though nonhuman primates do not have language, they nonetheless have interesting thoughts.

Bibliography:

1. Allman, J. (1999). Evolving brains. New York: Wiley.
2. Alvarez-Buylla, A., Kirn, J. R., & Nottebohm, F. (1990). Birth of projection neurons in adult avian brain may be related to perceptual or motor learning. Science, 249, 1444–1446.
3. Alvarez-Buylla, A., Theelen, M., & Nottebohm, F. (1988). Birth of projection neurons in the higher vocal center of the canary forebrain before, during, and after song learning. Proceedings of the National Academy of Sciences, 85, 8722–8726.
4. Antell, S., & Keating, D. P. (1983). Perception of numerical invariance in neonates. Child Development, 54, 695–701.
5. Balaban, E. (1997). Changes in multiple brain regions underlie species differences in a complex, congenital behavior. Proceedings of the National Academy of Sciences, 94, 2001–2006.
6. Balda, R. P., Kamil, A. C., & Bednekoff, P. A. (1997). Predicting cognitive capacities from natural histories: Examples from four Corvid species. Current Ornithology, 13, 33–66.
7. Bickerton, D. (1990). Species and language. Chicago: University of Chicago Press.
8. Blaser, E., Pylyshyn, Z., & Holcombe, A. O. (2000). Tracking an object through feature space. Nature, 408, 196–199.
9. Bornstein, M. H. (1987). Perceptual categories in vision and audition. In S. Harnad (Ed.), Categorical perception (pp. 287–300). Cambridge, UK: Cambridge University Press.
10. Boysen, S. T. (1997). Representation of quantities by apes. Advances in the Study of Behavior, 26, 435–462.
11. Boysen, S. T., & Bernston, G. G. (1989). Numerical competence in a chimpanzee. Journal of Comparative Psychology, 103, 23–31.
12. Brannon, E. M., & Terrace, H. S. (1998). Ordering of the numerosities 1 to 9 by monkeys. Science, 282, 746–749.
13. Brannon, E. M., & Terrace, H. S. (2000). Representation of the numerosities 1–9 by rhesus macaques (Macaca mulatta). Journal of Experimental Psychology: Animal Behavior Processes, 26, 31–49.
14. Butterworth, B. (1999). What counts: How every brain is hardwired for math. New York: Free Press.
15. Byrne, R. W., & Russon, A. E. (1998). Learning by imitation: A hierarchical approach. Behavioral and Brain Sciences, 21, 667– 684.
16. Caramazza, A., Hillis, A., Leek, E. C., & Miozzo, M. (1994). The organization of lexical knowledge in the brain: Evidence from category and modality-specific deficits. In L. A. Hirschfield & S. A. Gelman (Eds.), Mapping the mind: Domain specificity in cognition and culture (pp. 68–84). Cambridge, UK: Cambridge University Press.
17. Caramazza, A., & Shelton, J. R. (1998). Domain-specific knowledge systems in the brain: The animate-inanimate distinction. Journal of Cognitive Neuroscience, 10, 1–34.
18. Carey, S. (in press). The origins of concepts. Cambridge, MA: MIT Press.
19. Carey, S., & Spelke, E. S. (1994). Domain-specific knowledge and conceptual change. In L. Herschfeld & S. Gelman (Eds.), Mapping the mind: Domain-specificity in cognition and culture (pp. 169–201). Cambridge, UK: Cambridge University Press.
20. Carey, S., & Spelke, E. S. (in press). On conceptual change: counting and number. In J. Mehler & L. Bonati (Eds.), Developmental cognitive science. Cambridge, MA: MIT Press.
21. Carroll, S. B., Weatherbee, S. D., & Langeland, J. A. (1995). Homeotic genes and the regulation and evolution of insect wing number. Nature, 375, 58–61.
22. Cheney, D. L., & Seyfarth, R. M. (1985). Social and non-social knowledge in vervet monkeys. Philosophical Transactions of the Royal Society of London, 308B, 187–201.
23. Cheney, D. L., & Seyfarth, R. M. (1988). Assessment of meaning and the detection of unreliable signals by vervet monkeys. Animal Behaviour, 36, 477–486.
24. Cheney, D. L., & Seyfarth, R. M. (1990). How monkeys see the world: Inside the mind of another species. Chicago: University of Chicago Press.
25. Cheng, K. (1986). A purely geometric module in the rat’s spatial representation. Cognition, 23, 149–178.
26. Chomsky, N. (1957). Syntactic structures. The Hague, The Netherlands: Mouton.
27. Chomsky, N. (1965). Aspects of the theory of syntax. Cambridge, MA: MIT Press.
28. Chomsky, N. (1966). Cartesian linguistics. New York: Harper and Row.
29. Chomsky, N. (1988). Language and problems of knowledge. Cambridge, MA: MIT Press.
30. Church, R. M., & Boradbent, H. A. (1990). Alternative representations of time, number, and rate. Cognition, 37, 55–81.
31. Cleveland, J., & Snowdon, C. T. (1981). The complex vocal repertoire of the adult cotton-top tamarin, Saguinus oedipus oedipus. Zeitschrift fur Tierpsychologie, 58, 231–270.
32. Clutton-Brock, T. H. (1992). The evolution of parental care. Princeton, NJ: Princeton University Press.
33. Cowan, N. (2001). The magical number 4 in short-term memory: a reconsideration of mental storage capacity. Behavioral and Brain Sciences, 24, 5–43.
34. D’Amato, M., & Colombo, M. (1990). The symbolic distance effect in monkeys (Cebus apella). Animal learning and behavior, 18, 133–140.
35. Davies, N. B. (2000). Cuckoos, cowbirds and other cheats. New York: Academic Press.
36. Deacon, T. W. (1997). The symbolic species: The co-evolution of language and the brain. New York: Norton.
37. Deaner, R. O., Nunn, C. L., & van Schaik, C. P. (2000). Comparative tests of primate cognition: different scaling methods produce different results. Brain, Behavior and Evolution, 232, 1–8.
38. Dehaene, S. (1997). The number sense. Oxford, UK: Oxford University Press.
39. Dehaene, S. (2000). Cerebral bases of number processing and calculation. In M. Gazzaniga (Ed.), The new cognitive neurosciences. (2nd ed., pp. 987–998). Cambridge, MA: MIT Press.
40. Dent, M. L., Brittan-Powell, F., Dooling, R. J., & Pierce, A. (1997). Perception of synthetic /ba/-/wa/ speech continuum by budgerigars (Melopsittacus undulatus). Journal of the Acoustical Society of America, 102, 1891–1897.
41. Di Fiore, A., & Rendall, D. (1994). Evolution of social organization: a reappraisal for primates by using phylogenetic methods. Proceedings of the National Academy of Sciences, 91, 9941–9945.
42. Dittus, W. P. G. (1984). Toque macaque food calls: Semantic communication concerning food distribution in the environment. Animal Behaviour, 32, 470–477.
43. Doupe, A. J., Brainard, M. S., & Hessler, N. A. (2000). The song system: neural circuits essential throughout life for vocal behavior and plasticity. In M. Gazzaniga (Ed.), The new cognitive neurosciences (pp. 451–468). Cambridge, MA: MIT Press.
44. Ehret, G., & Haack, B. (1981). Categorical perception of mouse pup ultrasounds by lactating females. Naturwissenshaften, 68,
45. Eimas, P. D., Siqueland, P., Jusczyk, P., & Vigorito, J. (1971). Speech perception in infants. 171, 303–306.
46. Evans, C. S., & Marler, P. (1995). Language and animal communication: Parallels and contrasts. In H. Roitblatt (Ed.), Comparative approaches to cognitive science (pp. 241–282). Cambridge, MA: MIT Press.
47. Feigenson, L., Carey, S., & Hauser, M. D. (2002). The representations underlying infants’choice of more: Object files versus analog magnitudes. Psychological Science, 13, 150–156.
48. Feigenson, L., Carey, S., & Spelke, E. S. (2002). Infants’ discrimination of number vs. continuous extent. Cognitive Psychology 44, 33–66.
49. Fischer, J. (1998). Barbary macaques categorize shrill barks into two call types. Animal Behaviour, 55, 799–807.
50. Fisher, J., & Hinde, R. A. (1949). The Opening of milk bottles by birds. British Birds, 42, 347–357.
51. Fitch, W. T. (2000). The evolution of speech: a comparative review. Trends in Cognitive Sciences, 4, 258–267.
52. Fodor, J. A. (1975). The language of thought. Cambridge, MA: Harvard University Press.
53. Fodor, J. A. (1983). The modularity of mind. Cambridge, MA: MIT Press.
54. Fodor, J. A. (2000). The mind doesn’t work that way. Cambridge, MA: MIT Press.
55. Galef, B. G., Jr. (1992). The question of animal culture. Human Nature, 3, 157–178.
56. Gallistel, C. R. (1990). The organization of learning. Cambridge, MA: MIT Press.
57. Gallistel, C. R., & Gelman, R. (2000). Non-verbal numerical cognition: from reals to integers. Trends in Cognitive Sciences, 4, 59–65.
58. Gardner, R. A., & Gardner, B. T. (1969). Teaching sign language to a chimpanzee. Science, 165, 664–672.
59. Gelman, R., & Gallistel, C. R. (1986). The child’s understanding of number. Cambridge, MA: Harvard University Press.
60. Gerhart, J., & Kirschner, M. (1997). Cells, embryos, and evolution. Oxford, UK: Blackwell Scientific.
61. Gibbon, J. (1977). Scalar expectancy theory and Weber’s Law in animal timing. Psychological Review, 84, 279–335.
62. Gibbon, J., Malapani, C., Dale, C. L., & Gallistel, C. R. (1997). Toward a neurobiology of temporal cognition: advances and challenges. Current Opinions in Neurobiology, 7, 170–184.
63. Gouteux, S., Thinus-Blanc, C., & Vauclair, J. (2001). Rhesus monkeys use geometric and non-geometric information during a reorientationtask.JournalofExperimentalPsychology:General, 130, 505–519.
64. Gouzoules, S., Gouzoules, H., & Marler, P. (1984). Rhesus monkey (Macaca mulatta) screams: representational signalling in the recruitment of agonistic aid. Animal Behaviour, 32, 182–193.
65. Hailman, J. P., & Ficken, M. S. (1987). Combinatorial animal communication with computable syntax: Chick-a-dee calling qualifies as ‘language’by structural linguistics. Animal Behaviour, 34, 1899–1901.
66. Harcourt, A. H., & de Waal, F. B. M. (1992). Coalitions and alliances in humans and other animals. Oxford, UK: Oxford University Press.
67. Harnad, S. (1987). Categorical perception: The groundwork of cognition. Cambridge, UK: Cambridge University Press.
68. Hauser, M. D. (1996). The evolution of communication. Cambridge, MA: MIT Press.
69. Hauser, M. D. (1997). Artifactual kinds and functional design features: What a primate understands without language. Cognition, 64, 285–308.
70. Hauser, M. D. (1998). Functional referents and acoustic similarity: Field playback experiments with rhesus monkeys. Animal Behaviour, 55, 1647–1658.
71. Hauser, M. D. (2000). Wild minds: What animals really think. New York: Henry Holt.
72. Hauser, M. D., & Carey, S. (1998). Building a cognitive creature from a set of primitives: Evolutionary and developmental insights. In D. Cummins & C. Allen (Eds.), The evolution of mind (pp. 51–106). Oxford, UK: Oxford University Press.
73. Hauser, M. D., & Carey, S. (in preparation). Limits on spontaneous number processing in rhesus monkeys: Evidence from an expectancy violation procedure. Manuscript in review.
74. Hauser, M. D., Carey, S., & Hauser, L. B. (2000). Spontaneous number representation in semi-free-ranging rhesus monkeys. Proceedings of the Royal Society, London, 267, 829–833.
75. Hauser, M. D., MacNeilage, P., & Ware, M. (1996). Numerical representations in primates. Proceedings of the National Academy of Sciences, 93, 1514–1517.
76. Hauser, M. D., Newport, E. L., & Aslin, R. N. (2001). Segmenting a continuous acoustic speech stream: Serial learning in cotton-top tamarin monkeys. Cognition, 78, B58–B64.
77. Haxby, J. V., Hoffman, E. A., & Gobbini, M. I. (2000). The distributed human neural system for face perception. Trends in Cognitive Science, 4, 223–232.
78. Healy, S. (1998). Spatial representation in animals. Oxford, UK: Oxford University Press.
79. Herman, L. M., & Uyeyama, R. K. (1999). The dolphin’s grammatical competency: Comments on Kako (1999). Animal Learning and Behavior, 27, 18–23.
80. Hermer, L., & Spelke, E. S. (1994). A geometric process for spatial reorientation in young children. Nature, 370, 57–59.
81. Hermer, L., & Spelke, E. S. (1996). Modularity and development: The case of spatial reorientation. Cognition, 61, 195–232.
82. Hermer-Vazquez, L., Spelke, E., & Katsnelson, A. (1999). Sources of flexibility in human cognition: Dual-task studies of space and language. Cognitive Psychology, 39, 3–36.
83. Heyes, C. M., & Galef, B. G. (1996). Social learning in animals: The roots of culture. San Diego, CA: Academic Press.
84. Heyes, C. M., & Huber, L. (2000). The evolution of cognition. Cambridge, MA: MIT Press.
85. Hirschfeld, L. A., & Gelman, S. A. (1994). Mapping the mind: Domain specificity in cognition and culture. Cambridge, UK: Cambridge University Press.
86. Huber, E. (1931). Evolution of the facial musculature and facial expression. Baltimore: Johns Hopkins University Press.
87. Jackendoff, R. (1999). Possible stages in the evolution of the language capacity. Trends in Cognitive Science, 3, 272–279.
88. Jenkins, W. M., Merzenich, M. M., Ochs, M. T., Allard, T., & GuicRobles,E.(1990).Functionalreorganizationofprimarsomatosensory cortex in adult owl monkeys after behaviorally controlled tactile stimulation. Journal of Neurophysiology, 63, 82–104.
89. Jusczyk, P. W. (1997). The discovery of spoken language. Cambridge, MA: MIT Press.
90. Kaas, J. H. (2000). The reorganization of sensory and motor maps after injury in adult mammals. In M. Gazzaniga (Ed.), The new cognitive neurosciences (pp. 223–236). Cambridge, MA: MIT Press.
91. Kahneman, D., Treisman, A., & Gibbs, B. (1992). The reviewing of object files: Object specific integration of information. Cognitive Psychology, 24, 175–219.
92. Kanwisher, N., Downing, P., Epstein, R., & Kourtzi, Z. (in press). Functional neuroimaging of human visual recognition. In Kingstone & Cabeza (Eds.), The handbook on functional neuroimaging. Cambridge, MA: MIT Press.
93. Kanwisher, N., McDermott, J., & Chun, M. M. (1997). The fusiform face area: A module in human extrastriate cortex specialized for face perception. Journal of Neuroscience, 17, 4302–4311.
94. Kawai, N., & Matsuzawa, T. (2000). Numerical memory span in a chimpanzee. Nature, 403, 39–40.
95. Keil, F. C. (1994). The birth and nurturance of concepts by domains: The origins of concepts of living things. In L. A. Hirschfield & S. A. Gelman (Eds.), Mapping the mind: Domain specificity in cognition and culture (pp. 234–254). Cambridge, UK: Cambridge University Press.
96. Kilgard, M. P., & Merzenich, M. M. (1998). Cortical reorganization enabled by nucleus basalis activity. Science, 278, 1714–1718.
97. Kilner, R. M., Noble, D. G., & Davies, N. B. (1999). Signals of need in parent-offspring communication and their exploitation by the common cuckoo. Nature, 397, 667–672.
98. Kluender, K. R., Diehl, R., & Killeen, P. R. (1987). Japanese quail can learn phonetic categories. Science, 237, 1195–1197.
99. Kluender, K. R., Lotto, A. J., Holt, L. L., & Bloedel, S. L. (1998). Role of experience for language-specific functional mappings of vowel sounds. Journal of the Acoustical Society of America, 104, 3568–3582.
100. Koechlin, E., Dehaene, S., & Mehler, J. (1997). Numerical transformations in five-month old human infants. Mathematical Cognition, 3, 89–104.
101. Kuhl, P. K. (1989). On babies, birds, modules, and mechanisms: A comparative approach to the acquisition of vocal communication. In R. J. Dooling & S. H. Hulse (Eds.), The comparative psychology of audition (pp. 379–422). Hillsdale, NJ: Erlbaum.
102. Kuhl, P. K. (1991). Human adults and human infants show a “perceptual magnet effect” for the prototypes of speech categories, monkeys do not. Perception and Psychophysics, 50, 93–107.
103. Kuhl, P. K. (2000). Language, mind, and brain: Experience alters perception. In M. Gazzaniga (Ed.), The new cognitive neurosciences (2nd ed., pp. 99–118). Cambridge, MA: MIT Press.
104. Kuhl, P. K., & Miller, J. D. (1975). Speech perception by the chinchilla: Voiced-voiceless distinction in alveolar plosive consonants. Science, 190, 69–72.
105. Kuhl, P. K., & Padden, D. M. (1982). Enhanced discriminability at the phonetic boundaries for the voicing feature in macaques. Perception and Psychophysics, 32, 542–550.
106. Kuhl, P. K., & Padden, D. M. (1983). Enhanced discriminability at the phonetic boundaries for the place feature in macaques. Journal of the Acoustical Society of America, 73, 1003–1010.
107. Kuhl, P. K.,Williams, K.A., Lacerda, F., Stevens, K. N., & Lindblom, B. (1992). Linguistic experience alters phonetic perception in infants by 6 months of age. Science, 255, 606–608.
108. Leslie, A. M., Xu, F., Tremoulet, P. D., & Scholl, B. J. (1998). Indexing and the object concept: Developing ‘what’ and ‘where’ systems. Trends in Cognitive Science, 2, 10–18.
109. Liberman, A. M., Cooper, F. S., Shankweiler, D. P., & StuddertKennedy, M. (1967). Perception of the speech code. Psychological Review, 74, 431–461.
110. Liberman, A. M., Delattre, P. C., & Cooper, F. S. (1958). Some rules for the distinction between voiced and voiceless stops in initial position. Language and Speech, 1, 153–167.
111. Liberman, A. M., Harris, K. S., Hoffman, H. S., & Griffith, B. C. (1957). The discrimination of speech sounds within and across phoneme boundaries. Journal of Experimental Psychology, 54, 358–368.
112. Liberman, A. M., & Mattingly, I. G. (1985). The motor theory of speech perception revised. Cognition, 21, 1–36.
113. Liberman, A. M., & Mattingly, I. G. (1988). Specialized perceiving systems for speech and other biologically significant sounds. In G. M. Edelman, W. E. Gail, & W. M. Cowan (Eds.), Auditory function (pp. 775–793). New York: Wiley.
114. Lieberman, P. (1968). Primate vocalizations and human linguistic ability. Journal of the Acoustical Society of America, 44, 1574–1584.
115. Lieberman, P. (1984). The biology and evolution of language. Cambridge, MA: Harvard University Press.
116. Lieberman, P., Klatt, D. H., & Wilson, W. H. (1969). Vocal tract limitations on the vowel repertoires of rhesus monkeys and other nonhuman primates. Science, 164, 1185–1187.
117. Logothetis, N. K., & Sheinberg, D. L. (1996). Visual object recognition. Annual Review of Neuroscience, 19, 577–621.
118. Lotto, A. J., Kluender, K. R., & Holt, L. L. (1998). Depolarizing the perceptual magnet effect. Journal of the Acoustical Society of America, 103, 3648–3655.
119. MacNeilage, P. F. (1998). The frame/content theory of evolution of speech production. Behavioral and Brain Sciences, 21, 499–546.
120. Macphail, E. (1987a). The comparative psychology of intelligence. Behavioral and Brain Sciences, 10, 645–695.
121. Macphail, E. (1987b). Intelligence: A comparative approach. In C. Blakemore & S. Greenfield (Eds.), Mindwaves: Thoughts on intelligence, identity and consciousness (pp. 177–194). Oxford, UK: Basil Blackwell.
122. Marler, P. (1978). Primate vocalizations: Affective or symbolic? In G. Bourne (Ed.), Progress in ape research (pp. 85–96). New York: Academic Press.
123. Marler, P., Dufty, A., & Pickert, R. (1986). Vocal communication in the domestic chicken. Pt. 1. Does a sender communicate information about the quality of a food referent to a receiver? Animal Behaviour, 34, 188–193.
124. Matsuzawa, T. (1985). Use of numbers by a chimpanzee. Nature, 315, 57–59.
125. May, B., Moody, D. B., & Stebbins, W. C. (1989). Categorical perception of conspecific communication sounds by Japanese macaques, Macaca fuscata. Journal of the Acoustical Society of America, 85, 837–847.
126. McComb, K., Packer, C., & Pusey, A. (1994). Roaring and numerical assessment in contests between groups of female lions, Panthera leo. Animal Behaviour, 47, 379–387.
127. Mechner, F. (1958). Probability relations within response sequences under ratio reinforcement. Journal of the Experimental Analysis of Behavior, 1, 109–122.
128. Meck, W. H., & Church, R. M. (1983). A mode control model of counting and timing processes. Journal of Experimental Psychology: Animal Behavior Processes, 9, 320–334.
129. Mix, K. S., Levine, S. C., & Huttenlocher, J. (1997). Numerical abstraction in infants: another look. Developmental Psychology, 33, 423–428.
130. Moyer, R. S., & Landauer, T. K. (1967). Time required for judgements of numerical inequality. Nature, 215, 1519–1520.
131. Needham, A., & Baillargeon, R. (2000). Infants’ use of featural and experiential information in segregating and individuating objects: A reply to Xu, Carey, and Welch. Cognition, 74, 255–284.
132. Nelson, D. A., & Marler, P. (1989). Categorical perception of a natural stimulus continuum: Birdsong. Science, 244, 976–978.
133. Olthof, A., Iden, C. M., & Roberts, W. A. (1997). Judgement of ordinality and summation of number by squirrel monkeys. Journal of Experimental Psychology: Animal Behavior Processes, 23, 325–339.
134. Orlov, T., Yakoviev, V., Hochstein, S., & Zohary, E. (2000). Macaque monkeys categorize images by their ordinal number. Nature, 404, 77–80.
135. Pepperberg, I. M. (1994). Numerical competence in an African gray parrot (Psittacus erithacus). Journal of Comparative Psychology, 108, 36–44.
136. Pepperberg, I. M. (2000). The Alex studies. Cambridge, MA: Harvard University Press.
137. Perrett, D. I., Mistlin, A. J., Chitty, A. J., Smith, P. A., Potter, D. D., Broennimann, R., & Haries, M. (1988). Specialized face processing and hemispheric asymmetry in man and monkey: evidence from single unit and reaction time studies. Behavioural Brain Research, 29, 245–258.
138. Perrett, D. I., Smith, A. J., Potter, D. D., Mistlin, A. J., Head, A. S., Milner, A. D., & Jeeves, M. A. (1984). Neurones responsive to faces in the temporal cortex: Studies of functional organization, sensitivity to identity and relation to perception. Human Neurobiology, 3, 197–208.
139. Pinker, S. (1994). The language instinct. New York: William Morrow.
140. Pinker, S. (1997). How the mind works. New York: W. W. Norton.
141. Pinker, S., & Bloom, P. (1990). Natural language and natural selection. Behavioral and Brain Sciences, 13, 707–784.
142. Platt, J. R., & Johnson, D. M. (1971). Localization of position within a homogeneous behavior chain: Effects of error contingencies. Learning and Motivation, 2, 386–414.
143. Premack, D. (1986). Gavagai! or the future history of the animal language controversy. Cambridge, MA: MIT Press.
144. Ramachandran, V. S. (1993). Behavioral and magnetoencephalographic correlates of plasticity in the adult brain. Proceedings of the National Academy of Sciences, 90, 10413–10420.
145. Ramus, F., Hauser, M. D., Miller, C. T., Morris, D., & Mehler, J. (2000). Language discrimination by human newborns and cotton-top tamarins. Science, 288, 349–351.
146. Reboreda, J. C., Clayton, N. S., & Kacelnik, A. (1996). Species and sex differences in hippocampus size in parasitic and nonparasitic cowbirds. Neuroreport, 7, 505–508.
147. Recanzone, G. H. (2000). Cerebral cortical plasticity: Perception and skill acquisition. In M. Gazzaniga (Ed.), The new cognitive neurosciences (pp. 237–247). Cambridge, MA: MIT Press.
148. Remez, R. E., Rubin, P. E., Pisoni, D. B., & Carrell, T. D. (1981). Speech perception without traditional speech cues. Science, 212, 947–950.
149. Ridley, M. (1996). The origins of virtue. New York: Viking Press.
150. Robinson, J. G. (1979). An analysis of the organization of vocal communication in the titi monkey. Callicebus moloch. Zeitschrift fur Tierpsychologie, 49, 381–405.
151. Robinson, J. G. (1982). Vocal systems regulating within-group spacing. In C. T. Snowdon, C. R. Brown, & M. R. Petersen (Eds.), Primate communication (pp. 94–116). Cambridge, UK: Cambridge University Press.
152. Rolls, E. T. (2000). Functions of the primate temporal lobe cortical visual areas in invariant visual object and face recognition. Neuron, 27, 205–218.
153. Rumbaugh, D. M., & Washburn, D. A. (1993). Counting by chimpanzees and ordinality judgements by macaques in videoformatted tasks. In S. T. Boysen & E. J. Capaldi (Eds.), The development of numerical competence: Animal and human models (pp. 87–108). Hillsdale, NJ: Erlbaum.
154. Saffran, J. R., Aslin, R. N., & Newport, E. L. (1996). Statistical learning by 8-month-old infants. Science, 274, 1926–1928.
155. Saffran, J. R., Johnson, E., Aslin, R. N., & Newport, E. (1999). Statistical learning of tone sequences by human infants and adults. Cognition, 70, 27–52.
156. Santos, L. R., Hauser, M. D., & Spelke, E. S. (2001). Recognition and categorization of biologically significant objects in rhesus monkeys (Macaca mulatta): The domain of food. Cognition, 82, 127–155.
157. Savage-Rumbaugh, E. S. (1986). Ape language: From conditioned response to symbol. New York: Columbia University Press.
158. Savage-Rumbaugh, E. S., Murphy, J., Sevcik, R. A., Brakke, K. E., Williams, S. L., & Rumbaugh, D. M. (1993). Language comprehension in ape and child. Monographs of the Society for Research in Child Development, 58, 1–221.
159. Scholl, B. J., & Pylyshyn, Z. W. (1999). Tracking multiple items through occlusion: Clues to visual objecthood. Cognitive Psychology, 38, 259–290.
160. Seyfarth, R. M., Cheney, D. L., & Marler, P. (1980a). Monkey responses to three different alarm calls: Evidence of predator classification and semantic communication. Science, 210, 801– 803.
161. Seyfarth, R. M., Cheney, D. L., & Marler, P. (1980b). Vervet monkey alarm calls: semantic communication in a free-ranging primate. Animal Behaviour, 28, 1070–1094.
162. Sherry, D. F. (1997). Cross-species comparisons. In M. Daly (Ed.), Characterizinghumanpsychologicaladaptations(pp. 181–194). New York: Wiley.
163. Sherry, D. F. (2000). What sex differences in spatial ability tell us about the evolution of cognition. In M. Gazzaniga (Ed.), The new cognitive neurosciences (2nd ed., pp. 1209–1217). Cambridge, MA: MIT Press.
164. Sherry, D. F., Forbes, M. R. L., Khurgel, M., & Ivy, G. O. (1993). Females have a larger hippocampus than males in the broodparasitic brown-headed cowbird. Proceedings of the National Academy of Sciences, 90, 7839–7843.
165. Sherry, D. F., & Galef, B. G. (1984). Cultural transmission without imitation: Milk bottle opening by birds. Animal Behaviour, 32, 937–938.
166. Sherry, D. F., & Galef, B. G. (1990). Social learning without imitation: More about milk bottle opening by birds. Animal Behaviour, 40, 987–989.
167. Shettleworth, S. (1998). Cognition, evolution and behavior. New York: Oxford University Press.
168. Simon, T. J. (1997). Reconceptualizing the origins of number knowledge: A “non-numerical” account. Cognitive Development, 12, 349–372.
169. Simon, T. J., Hespos, S., & Rochat, P. (1995). Do infants understand simple arithmetic? A replication of Wynn (1992). Cognitive Development, 10, 253–269.
170. Sinnott, J. M. (1989). Detection and discrimination of synthetic English vowels by OldWorld monkeys (Cercopithecus, Macaca) and humans. Journal of the Acoustical Society of America, 86, 557–565.
171. Sinnott, J. M., & Brown, C. H. (1997). Perception of the English liquid/ra-la/ contrast by humans and monkeys. Journal of the Acoustical Society of America, 102, 588–602.
172. Sinnott, J. M., Petersen, M. R., & Hopp, S. L. (1985). Frequency and intensity discrimination in humans and monkeys. Journal of the Acoustical Society of America, 78, 1977–1985.
173. Snowdon, C. T. (1987). A naturalistic view of categorical perception. In S. Harnad (Ed.), Categorical perception (pp. 332–354). Cambridge, UK: Cambridge University Press.
174. Sommers, M. S., Moody, D. B., Prosen, C. A., & Stebbins, W. C. (1992). Formant frequency discrimination by Japanese macaques (Macaca fuscata). Journal of the Acoustical Society of America, 91, 3499–3510.
175. Spelke, E. S. (1979). Perceiving bimodally specified events in infancy, Developmental Psychology, 15, 626–636.
176. Spelke, E. S., Born, W. S., & Chu, F. (1983). Perception of moving, sounding objects by 4-month-old infants. Perception, 12, 719– 732.
177. Staddon, J. E. R., & Higa, J. J. (1999). Time and memory: Towards a pacemaker-free theory of interval timing. Journal of the Experimental Analysis of Behavior, 71, 215–251.
178. Starkey, P., & Cooper, R. (1980). Perception of numbers by human infants. Science, 210, 1033–1035.
179. Starkey, P., Spelke, E. S., & Gelman, R. (1990). Numerical abstraction by human infants. Cognition, 36, 97–127.
180. Stebbins, W. C. (1983). The acoustic sense of animals. Cambridge, UK: Harvard University Press.
181. Stephens, D., & Krebs, J. R. (1986). Optimal foraging theory. Princeton, NJ: Princeton University.
182. Strauss, M. S., & Curtis, L. E. (1981). Infant perception of numerosity. Child Development, 52, 1146–1152.
183. Struhsaker, T. T. (1967). Auditory communication among vervet monkeys (Cercopithecus aethiops). In S. A. Altmann (Ed.), Social communication among primates (pp. 281–324). Chicago: Chicago University Press.
184. Studdert-Kennedy, M. (1998). The particulate origins of language generativity: From syllable to gesture. In J. Hurford, M. Studdert-Kennedy, & C. Knight (Eds.), Approaches to the evolution of language: Social and cognitive bases (pp. 202–221). Cambridge, UK: Cambridge University Press.
185. Sulkowski, G. M., & Hauser, M. D. (2001). Can rhesus monkeys spontaneously subtract? Cognition, 79, 239–262.
186. Tarr, M. J., & Gauthier, I. (2000). FFA: A flexible fusiform area for subordinate-level visual processing automatized by expertise. Nature Neuroscience, 3, 764–769.
187. Terrace, H. (1993). The phylogeny and ontogeny of serial memory: List learning by pigeons and monkeys. Psychological Science, 4, 162–169.
188. Terrace, H., Chen, S., & Newman, A. (1995). Serial learning with a wild card by pigeons: Effect of list length. Journal of Comparative Psychology, 109, 162–172.
189. Thomas, R. K., Fowlkes, D., & Vickery, J. D. (1980). Conceptual numerousness judgments by squirrel monkeys. American Journal of Psychology, 93, 247–257.
190. Tomasello, M., Kruger, A., & Ratner, H. (1993). Cultural learning. Behavioral and Brain Sciences, 16, 495–552.
191. Trivers, R. L. (1972). Parental investment and sexual selection. In B. Campbell (Ed.), Sexual selection and the descent of man (pp. 136–179). Chicago: Aldine Press.
192. Trout, J. D. (2000). The biological basis of speech: what to infer from talking to the animals. Psychological Review, 143, 112–146.
193. Uller, C. (1997). Origins of numerical concepts: A comparative study of human infants and nonhuman primates. Unpublished doctoral dissertation, MIT, Cambridge, MA.
194. Uller, C., Carey, S., Huntley-Fenner, G., & Klatt, L. (1999). What representations might underlie infant numerical knowledge. Cognitive Development, 14, 1–36.
195. Uller, C., Hauser, M. D., & Carey, S. (2001). Spontaneous representation of number in cotton-top tamarins. Journal of Comparative Psychology, 115, 248–257.
196. Vallortigara, G., Zanforlin, M., & Pasti, G. (1990). Geometric modules in animals’ spatial representations: A test with chicks (Gallus gallus domesticus). Journal of Comparative Psychology, 104, 248–254.
197. Vander Wall, S. B. (1990). Food hoarding in animals. Chicago: University of Chicago Press.
198. Wallman, J. (1992). Aping language. New York: Cambridge University Press.
199. Washburn, D. A., & Rumbaugh, D. M. (1991). Ordinal judgements of numerical symbols by macaques (Macaca mulatta). Psychological Science, 2, 190–193.
200. Weiss, D. J., Ghazanfar,A.A., Miller, C. T., & Hauser, M. D. (2002). Specialized processing of primate facial and vocal expressions: Evidence for cerebral asymmetries. In L. Rogers & R. Andrews (Eds.), Cerebral vertebrate lateralization (pp. 480–530). New York: Cambridge University Press.
201. Whalen, J., Gallistel, C. R., & Gelman, R. (1999). Nonverbal counting in humans: The psychophysics of number representation. Psychological Science, 10, 130–137.
202. Whiten, A., Goodall, J., McGrew, W. C., Nishida, T., Reynolds, V., Sugiyama, Y., Tutin, C. E. G., Wrangham, R. W., & Boesch, C. (1999). Cultures in chimpanzees. Nature, 399, 682–685.
203. Whiten, A., & Ham, R. (1992). On the nature and evolution of imitation in the animal kingdom: Reappraisal of a century of research. In P. J. B. Slater, J. S. Rosnblatt, C.Beer, & M. Milinski (Eds.), Advances in the study of behavior (pp. 239–283). New York: Academic Press.
204. Wilson, J. Q. (1987). The moral sense. New York: Basic Books.
205. Wilson, M. L., Hauser, M. D., & Wrangham, R. W. (2001). Does participation in cooperative intergroup conflict depend on numerical assessment, range location or rank for wild chimpanzees? Animal Behaviour, 61, 1203–1216.
206. Wright, A. A., & Rivera, J. J. (1997). Memory of auditory lists by rhesus monkey (Macaca mulatta). Journal of Experimental Psychology: Animal Behavior Processes, 23, 441–449.
207. Wynn, K. (1992). Addition and subtraction by human infants. Nature, 358, 749–750.
208. Wynn, K. (1996). Infants’individuation and enumeration of actions. Psychological Science, 7, 164–169.
209. Wynn, K. (1998). Psychological foundations of number: Numerical competence in human infants. Trends in Cognitive Sciences, 2, 296–303.
210. Wyttenbach, R. A., & Hoy, R. R. (1999). Categorical perception of behaviorally relevant stimuli by crickets. In M. D. Hauser & M. Konishi (Eds.), The design of animal communication (pp. 559–576). Cambridge, MA: MIT Press.
211. Wyttenbach, R. A., May, M. L., & Hoy, R. R. (1996). Categorical perception of sound frequencies by crickets. Science, 273, 1542–1544.
212. Xu, F., & Carey, S. (1996). Infants’ metaphysics: The case of numerical identity. Cognitive Psychology, 30, 111–153.
213. Xu, F., & Carey, S. (2000). The emergence of kind concepts: A rejoinder to Needham and Baillargeon. Cognition, 74, 285–301.
214. Xu, F., Carey, S., & Welch, J. (1999). Infants’ ability to use object kind information for object individuation. Cognition, 70, 137– 166.
215. Xu, F., & Spelke, E. S. (2000). Large number discrimination in 6-month old infants. Cognition, 74, B1–B11.
216. Yang, T. T., Gallen, C. C., Ramachandran, V. S., Cobb, S., Schwartz, B. J., & Bloom, F. E. (1994). Noninvasive detection of cerebral plasticity in adult human somatosensory cortex. NeuroReport, 5, 701–704.
217. Ydenberg, R. C. (1998). Behavioral decisions about foraging and predator avoidance. In R. Dukas (Ed.), Cognitive ecology (pp. 343–378). Chicago: University of Chicago Press.
218. Zuberbuhler, K., Cheney, D. L., & Seyfarth, R. M. (1999). Conceptual semantics in a nonhuman primate. Journal of Comparative Psychology, 113, 33–42.
219. Zuberbuhler, K., Noe, R., & Seyfarth, R. M. (1997). Diana monkey long-distance calls: Messages for conspecifics and predators. Animal Behaviour, 53, 589–604.