View sample Theories Of Risk, Decision, And Choice Research Paper. Browse other research paper examples and check the list of research paper topics for more inspiration. If you need a religion research paper written according to all the academic standards, you can always turn to our experienced writers for help. This is how your paper can get an A! Feel free to contact our research paper writing service for professional assistance. We offer high-quality assignments for reasonable rates.
Risk is a central concept in everyday life as well as in many theories of the social and behavioral sciences. People have an intuitive notion about what is meant by risk. We are able to make risk judgments and we are able to compare the riskiness of alternatives. We might agree that it is riskier to invest in stocks than in bonds, and it might seem riskier to eat mushrooms which we have collected ourselves than mushrooms bought in a supermarket. Nevertheless, some people choose to buy stocks and others choose to eat mushrooms which they collected, i.e., they are willing to take the risk.
Academic Writing, Editing, Proofreading, And Problem Solving Services
Get 10% OFF with 24START discount code
The examples demonstrate that risk can be analyzed as a primitive and that risk can be analyzed in the context of choice. Theories which model risk as a primitive usually start from the assumption that for each individual there exists a meaningful risk ordering of alternatives which can be obtained directly by asking the individual. Theories that consider risk in the context of preference start from choice as a primitive. A definition of risk or riskiness of an alternative is then derived based on models of choice.
Throughout Sect. 1, the leading model of choice, expected utility, is considered. Based on this model, concepts of risk and riskiness are analyzed. Section 2 investigates theories that take risk as a primitive. In Sect. 3, risk value models are presented. They model choice in a way that explicitly considers risk, i.e., they combine the ideas of Sects. 1 and 2.
Throughout this research paper, only theories for the risk of random variables are presented. Random variables will be denoted X, Y, etc. and they will also be called lotteries or gambles. See Risk: Empirical Studies on Decision and Choice for what is known about the public’s judgments of the riskiness of physical, environmental, and material risk in ways that go beyond modeling these risks as random variables. An overview on risk-taking behavior can be found in Yates (1992).
1. Risk In The Context Of Expected Utility
The most widely used model of preference is von Neumann and Morgenstern’s (1947) expected utility model:
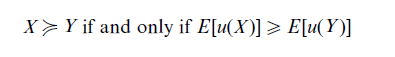
where u(.) is the utility function of an individual and E stands for expected value. The binary relation ≥ denotes ‘preferred or indifferent to.’ As expected utility results in an ordering of risky alternatives, it is called a theory for decision making under risk. However, utility theory offers no direct definition of risk or riskiness.
1.1 Risk Premium
One measure of risk in the context of expected utility could be the risk premium (RP), which is defined by the following equation:

The difference E [X ] – RP is also called the certainty equivalent of the lottery X. For reasons of simplicity, in the following only increasing utility functions are considered. If the risk premium is negative (positive), the expected utility of the lottery is larger (smaller) than the utility of the expected value of the lottery, i.e., the decision maker does (not) like the risk of the lottery, i.e., they behave in a risk seeking (risk averse) manner. A decision-maker with a risk premium of zero is labeled risk neutral. All risk premiums for nondegenerate lotteries (lotteries where no single consequence has a probability of one) are positive (negative, zero) if and only if the decision-maker’s utility function is concave (convex, linear).
Can the risk premium be used to define a risk ordering on lotteries, i.e., a binary relation ≥R, where X ≥R Y means that lottery X is at least as risky as lottery Y? Unfortunately, the answer is no. The risk premium depends on the initial wealth of the decision maker. If W and W denote two initial wealth levels, it is quite possible that RP(W + X ) > RP(W + Y ) and RP(W` + X ) < RP(W` + Y ). To define risk unambiguously, one must place restrictions on the utility function, or on the random variable.
1.2 Restrictions On The Utility Function
A classic restriction on the utility function is to assume that it has a quadratic form
![]()
where x denotes possible outcomes of the gamble X. In this case, the expected utility of a gamble X is given by
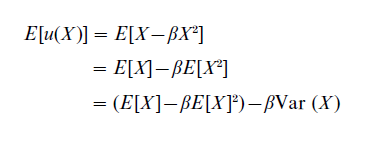
Thus, the expected utility is a function of expected value and variance. An increase in risk (measured by variance) implies a decrease in expected utility and vice versa. The coefficient β reflects the trade-off between risk and expected value. The risk ordering of lotteries implied by variance is independent of the decision-maker’s wealth level. For further cases where variance is a reasonable measure of risk, see Levy (1992). The general question to what extent expected utility can be interpreted as a risk value model is discussed in Sect. 3.
1.3 Restrictions On Random Variables
A classic restriction on the random variable is to compare only those that have identical expected values. For this case, Rothschild and Stiglitz (1970) were able to provide a definition of the risk of gambles. For E [X ] = E[Y ], we can say that X is more risky than Y if and only if the following three statements, which are equivalent, are true
(a) Every risk-averse decision maker prefers Y to X.
(b) X is equal to gamble Y plus noise, i.e., some random variable with expected value zero.
(c) X is obtained by a mean preserving spread of Y. A mean preserving spread takes probability weight from central parts of the distribution and puts it into the tails of the distribution while holding the expected value constant.
This definition of riskiness is convincing, but it is only applicable to lotteries with equal expected value, and thus yields a partial ordering of the space of gambles. To overcome this limitation, Jia and Dyer (1996) define a risk ordering on lotteries for concave utility functions u as follows
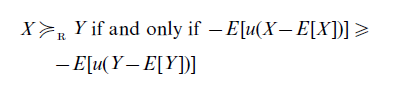
This definition of riskiness is able to order all lotteries. However, it is not clear to what extent this definition captures what people intuitively think about risk and how an ordering in terms of risk is related to an ordering in terms of preference. We will further investigate these questions in Sect. 3.
1.4 Relative Risk Aversion
All the results in this section are based on expected utility theory. However, it should be pointed out that utility functions not only measure decision-makers’ risk attitude, simultaneously they measure the marginal value of the good to be evaluated. An example should illustrate this point.
Suppose one has to evaluate a lottery which gives eight oranges if on a coin flip head comes up and zero oranges if tail comes up. Assume that the certainty equivalent is three oranges, i.e., the risk premium is one orange and thus the decision-maker is considered risk averse. Now, it could well be that this positive risk premium has nothing to do with any ‘intuitive’ notion of risk aversion. For instance, if the decision-maker likes three oranges half as much as eight oranges, then the average value of the lottery is equal to the value of three oranges, i.e., the risk premium can equally well be explained by some strength of preference considerations. The notion of relative risk aversion, introduced by Dyer and Sarin (1982), helps to disentangle strength of preference from utility. The concept of relative risk aversion defines risk aversion relative to the strength of preference. The above example shows a decision-maker who is relatively risk neutral.
2. Risk As A Primitive
In this section we start out with the assumption that subjects are able to meaningfully order lotteries with respect to their riskiness, i.e., that a risk ordering X ≥R Y exists. In Risk: Empirical Studies on Decision and Choice it is demonstrated that individuals are able to give consistent risk judgments. In this section we investigate how these judgments can be modeled. One has to look for a function R defined on the set of gambles with the property
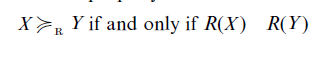
Every such function R will be called a risk measure. Note that we take subjects’ risk judgments (risk perception) as a primitive without giving an abstract definition of risk and without relating it to preference (see Brachinger and Weber 1997 for an overview).
2.1 Naive Measures Of Risk
The first class of risk measures to be discussed are so-called naive risk measures. Most of them are special cases of the following formula
![]()
where x0 is a benchmark (reference level of wealth) defining gains and losses, x` defines the range parameter that specifies what deviations are to be included in the risk measure, and α is a measure of relative impact of large and small deviations. Risk measures such as variance, semivariance, shortfall measures, probability of ruin (loss), etc., are all special cases of this risk measure. Some of these measures are quite popular, e.g., shortfall measures in the insurance and banking industry; nevertheless, they do not capture what individuals perceive as risk.
The fact that risk perception is not captured by variance, the measure most popular in economics and finance, can be demonstrated by a simple example. Consider the three two-outcome gambles X = (10, 0.5; -10, 0.5)—this is a gamble with a 50–50 chance of receiving 10 or -10-, Y = (20, 0.2; – 5, 0.8), and Z = (5, 0.8; – 20, 0.2). Empirical studies find that subjects consistently judge each of Z and Y to be more risky than X (Coombs and Bowen 1971), but expected value and variance are the same for all three lotteries. Higher moments of the distribution, e.g., skewness, have an influence on risk perception too.
2.2 Axiomatic Measures Of Risk: I
For a while it was quite popular to axiomatically derive measures of risk. Similar to what is done in modeling preferences, simple axioms of risk judgments were presented and measures of risk were derived mathematically. Pollatsek and Tversky (1970) were the first to use the axiomatic approach. Besides some technical axioms, they require a risk measure to be additive, i.e., the risk of the convolution of two lotteries should be equal to the sum of the risk of each lottery. This property implies, e.g., that the risk of a lottery played twice is equal to twice the risk of the lottery played once, and the risk ordering of two lotteries is not changed if they are both convoluted with the same lottery. Finally, they require that the risk of a lottery is reduced if a constant is added to all outcomes. From these conditions they derive the following risk measure
![]()
Thus, according to Pollatsek and Tversky (1970), the risk ordering is generated by a linear combination of expected value and variance. This model does not fit risk judgments since, for instance, the example given at the end of Sect. 2.1 demonstrates that subjects’ risk perception can not be explained just by expected value and variance.
Fishburn (1982, 1984) explored risk measurement from a purely axiomatic point of view. He considered gambles separated into gains and losses and did not specify functional forms, thus his theory remains rather general and is not considered further here.
2.3 Axiomatic Measures Of Risk: II
Luce (1980) was the first to derive risk measures from functional equations characterizing the effect of rescaling on perceived risk. His most prominent models consider the α-transformation Xα in which each outcome of the gamble X is multiplied by α > 0. He assumes that there exists an increasing function S (with S(1) =1), such that R(Xα) = R(αX ) = R(X ) S(α) for all X and α. He also assumes that the risk of a gamble X is the expectation of a transformation T of that gamble, i.e.,
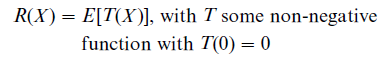
These assumptions imply the following risk measure
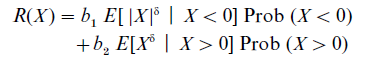
where δ is a positive real number, bi are weights on the components, and Prob (X > 0) denotes the probability that the random variable has outcomes greater than zero. This risk measure is a linear combination of the conditional expectation of negative and positive outcomes, where all outcomes are raised to the power δ.
Luce’s model was extended by Luce and Weber (1986). Influenced by empirical work and based on a system of axioms, they proposed the Conjoint Expected Risk (CER) model that has the following form
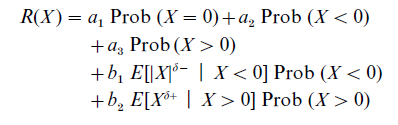
with ai and bi being weights on the components, and δ– and δ+ being coefficients of power functions. Empirical research has demonstrated that the CER model describes risk judgments reasonably well, admittedly at the cost of a rather large number of parameters in the model.
Sarin (1987) chose another way to extend Luce’s measure of risk. Instead of the α-transformation, he used a β-transformation, which just adds a factor β to all outcomes of the lottery. He then assumes that R(Xβ) = R(X + β) = R(X) S( β), with S a strictly decreasing function, S(0) = 1 and β > 0. This assumption mirrors the fact that the risk of a gamble appears to decrease when a β-transformation is applied. In conjunction with the expectation principle (see Luce’s approach), Sarin derived the following risk measure
![]()
with k > 0, c < 0 or k < 0 and c > 0. This risk measure gives higher weight to a gamble’s potential losses than to its potential gains. Both Sarin’s model and the CER model are able to capture the effect that subjects strongly dislike the possibility of large losses (potential catastrophes).
All the risk measures presented in Sects. 2.2 and 2.3 have the property that adding a constant (applying the β-transformation to the gamble) changes the risk, i.e., they are not location free. This property is supported by a lot of empirical work. However, on theoretical grounds, in quite a number of applications, e.g., in capital market theory, risk should be location free. Since nearly all the models proposed in Sect. 2.1 are location free, for certain applications it might be useful to combine the ideas of Sects. 2.2 and 2.3 with the concept of a location free risk measure. Weber (1990), therefore, advocates extending Sarin’s measure of risk to the following form, giving the risk measure some normative flavor
![]()
with k > 0, c < 0, which can be used in a capital market framework.
Recently, Jia et al. (1999) modified the model of Jia and Dyer (1996) presented in Sect. 1.3 to make it descriptively appealing. In Sect. 1.3, risk was defined as R*(X ) = – E [u(X – E [X ])] which is location free. To heal this deficiency, they propose the following measure of risk
![]()
where f (E [X ]) is a decreasing function of the expected value and R*(0) = – u(0) a constant. Thus, an increase in expected value leads to a decrease of risk—as in Sarin’s model. Their model is rather general as it only specifies that R*(X ) depends on the decision-maker’s utility function, but no specific form of the utility function is required.
3. Risk Value Models
Clearly, risk is related to preference (see also Sect. 1). To further investigate this relation, one could propose a general risk value model for evaluating gambles such that a gamble X is preferred to a gamble Y, i.e.,
![]()
where V measures the value of a gamble, R measures the risk, and f reflects the trade-off between these two components (see Sarin and Weber 1993 for a more extensive review). Clearly, a greater value is more preferred and a lower risk is more preferred. Therefore, f is increasing in V and decreasing in R.
Risk value models have an intuitive appeal, as people like to talk about the risk and the value of alternatives. There are two ways to use risk value models:
(a) Starting from expected utility, the EU model can be reformulated as a risk value model.
(b) A measure of risk as a primitive and the expected value can be the components of a risk value model.
Both ways still have their disadvantages. If one starts with expected utility (case (a)), in most cases it is not possible to find a straightforward decomposition into risk and value. It was shown in Sect. 1 that in order to do this one has to considerably restrict the utility function or the probability distribution. In addition, the risk measures derived from expected utility might not be descriptively correct. If one begins with a risk measure as a basis for a risk value model (case (b)), one has to first define a trade-off function f. It is by no means clear that the resulting risk value model will be prescriptively appealing. Future research hopefully will shed more light onto the relation between preference and risk.
Bibliography:
- Brachinger H W, Weber M 1997 Risk as a primitive: A survey of measures of perceived risk. OR Spektrum 19: 235–50
- Coombs C H, Bowen J N 1971 A test of VE-theories of risk and the effect of the central limit theorem. Acta Psychologica 35: 15–28
- Dyer J S, Sarin R K 1982 Relative risk aversion. Management Science 28: 875–86
- Fishburn P C 1982 Foundations of risk measurement. II. Effects of gains on risk. Journal of Mathematical Psychology 25: 226–42
- Fishburn P C 1984 Foundations of risk measurement. I. Risk as a probable loss. Management Science 30: 396–406
- Jia J, Dyer J S 1996 A standard measure of risk and risk-value models. Management Science 42: 1691–1705
- Jia J, Dyer J S, Butler J C 1999 Measures of perceived risk. Management Science 45: 519–32
- Levy H 1992 Stochastic dominance and expected utility: Survey and analysis. Management Science 38: 555–93
- Luce R D 1980 Several possible measures of risk. Theory and Decision 12: 217–28
- Luce R D, Weber E U 1986 An axiomatic theory of conjoint, expected risk. Journal of Mathematical Psychology 30: 188– 205
- Pollatsek A, Tversky A 1970 A theory of risk. Journal of Mathematical Psychology 7: 540–53
- Rothschild M, Stiglitz J E 1970 Increasing risk: I. A definition. Journal of Economic Theory 2: 225–43
- Sarin R K 1987 Some extensions of Luce’s measures of risk. Theory and Decision 22: 125–41
- Sarin R K, Weber M 1993 Risk-value models. European Journal of Operational Research 70: 135–49
- von Neumann J, Morgenstern O 1947 Theory of Games and Economic Behavior. Princeton University Press, Princeton, NJ
- Weber M 1990 Risikoentscheidungskalkule in der Finanzierungstheorie. C. E. Poeschel, Stuttgart, Germany
- Yates J F (ed.) 1992 Risk-taking Behavior. Wiley, Chichester, UK




