Self-Organizing Dynamical Systems Research Paper

Here, following a brief historical introduction, the main ideas of dynamical systems are described in a nontechnical fashion. The connection between notions of self-organization and nonlinear dynamical systems is then addressed as a foundation for understanding behavioral pattern formation, flexibility, and change. A flavor of the approach, which stresses an intimate relationship between theory and experiment, is addressed in the context of a few examples from the behavioral and social sciences. Finally, some extensions of the approach are discussed briefly, including a way to include meaningful information into the self-organizing dynamics.

1. A Short History Of Dynamical Systems

For the eighteenth century Scottish philosopher David Hume, all the sciences bore a relation to the human mind. In his Treatise of Human Nature (1738), Hume first divided the mind into its contents: ideas and impressions. Then he added dynamics, noting the impossibility of simple ideas forming more complex ones without some bond of union between them. Hume’s three dynamical laws for the association of ideas—resemblance, contiguity, and cause and effect—were thought to be responsible for controlling all mental operations. A kind of attraction, Hume thought, existed in the mental world: the motion of the mind was conceived as analogous to the motion of a body, as described earlier by Newton. Mental ‘stuff’ was governed (somehow) by dynamics.

All this has a strangely contemporary ring to it. Dynamics is not only the language of the natural sciences, but has permeated the social, behavioral, and neurosciences as well (Arbib et al. 1998, Kelso 1995, Vallacher and Novak 1997). Cognitive science, whose theory and paradigms are historically embedded in the language of the digital computer, may be the most recent of the human sciences to fall under the spell of dynamics (Port and van Gelder 1995, Thelen and Smith 1994).

Which factors led to the primacy of dynamics as the language of science, whether natural or human? First, was the insight of the French mathematician Henri Poincare to put dynamics into geometric form. Poincare introduced an array of powerful methods for visualizing how things behave, somewhat independent of the things themselves.

Second, following Poincare’s lead, were developments in understanding nonlinear dynamical systems from a mathematical point of view. These are sets of differential equations that can exhibit multiple solutions for the same parameters and are capable of highly irregular, even unpredictable behavior.

Third, was the ability to visualize how these equations behave by integrating them numerically on a digital computer. Parameters can be varied and parameter spaces explored without doing a ‘real’ experiment or collecting data of any kind. In fact, computer simulation and visualization is often the only possible method of exploring complex behavior.

Finally, were quite specific examples of cooperative (or ‘collective’) behavior in physics (e.g., fluids, lasers), chemistry (e.g., chemical reactions), biology (e.g., morphogenesis), and later, in the behavioral sciences. The behavioral experiments (Kelso 1984) and consequent theoretical modeling (Haken et al. 1985) showed for the first time that dynamic patterns of human behavior, how behavior forms, stabilizes, and changes, may be described quite precisely in the mathematical language of nonlinear dynamical systems. Not only were new effects predicted and observed, it was possible to derive these emergent patterns and the pattern dynamics by nonlinearly coupling the component parts. Since these early empirical and theoretical developments, ideas of self-organization and dynamics have infiltrated the social, behavioral, economic, and cognitive sciences, not to speak of literature and the arts.

2. Dynamical Systems: Some Terminology

What exactly is a dynamical system? It is not possible here to do justice to the mathematics of dynamical systems and its numerous technical applications, for example, in time series analysis (e.g., Strogatz 1994). For present purposes, only the basics are considered. Fundamentally, a dynamical system pertains to anything—such as the behavior of a human being or a social group—that evolves over time. Mathematically, if X₁, X₂ , …, X_n are the variables characterizing the system’s behavior, a dynamical system is a system of equations stipulating the temporal evolution of X, the vector of all permissible X-values. Therein lies the rub: in the social and behavioral sciences one has to find these Xs and identify their dynamics on a chosen level of description.

If X is a continuous function of time, then the dynamics of X is typically described by a set of first order ordinary differential equations (ODEs). The order of the equation refers to the highest derivative that appears in the equation. Thus, X = F (X ) is a first order equation where the dot above the X denotes the first derivative with respect to time and F (X ) gives the vector field. ODEs are of greatest interest when F is nonlinear because, depending on the particular form of F, a wide variety of behaviors can arise.

Another important class of dynamical system is difference equations or maps. Maps are often useful when the behavior of a system appears to be organized around discrete temporal events. Maps and ODEs provide complementary ways to model and study nonlinear dynamical behavior, but we shall not pursue maps further here (see, however, van Geert 1995 as an example of the approach).

A vectorfield is defined at each and every point of the state or phase space of the system, defined by the values of the variables X₁, X₂, …, X_n. As these states evolve in time they can be represented graphically as a trajectory. The state space is filled with trajectories. At any point in a given trajectory, a velocity vector can be determined by differentiation. These velocity vectors prescribe a velocity vectorfield, which is assumed to represent the flow or behavior of the dynamical system (Abraham and Shaw 1982). This flow often has characteristic tendencies particularly in dissipative systems, named thus because their state space volume decreases or dissipates over time toward attractors. In other words, trajectories converge over time (technically, as time goes to infinity) to subsets of the phase space (a given attractor’s basin of attraction). One may even think of an attractor as a representation of the goal of the behaving system (Saltzman and Kelso 1987).

The term transient defines the segment of a trajectory starting from some initial condition in the basin of attraction until it settles into an attractor. Attractors can be fixed points, in which all initial conditions converge to some stable rest state. Attractors can be periodic, exhibiting preferred rhythms or orbits on which the system settles regardless of where it starts. Or, there can be so-called strange attractors; strange because they exhibit deterministic chaos, a type of irregular behavior resembling random noise, yet often containing pockets of quite ordered behavior.

The presence of chaos in physical systems is ubiquitous, and there is some evidence suggesting that it may also play an important role in certain biological systems, including the human brain and its disorders (Kelso and Fuchs 1995). Chaos means sensitive dependence on initial conditions: nudging a chaotic system by just a hair can change its future behavior dramatically. In the vernacular, human behavior certainly seems ‘chaotic’ sometimes. However, although an area of active interest in many research fields, it remains unclear whether chaos, and its close relative, fractals (Mandelbrot 1982) provide any essential insights in the social and behavioral sciences.

What may be rather more important to appreciate is that parameters, so-called control parameters, can move a system through a vast array of different kinds of dynamic behavior of which chaos is only one. Thus, when a parameter changes smoothly, the attractor in general also changes smoothly. In other words, sizeable changes in the input have little or no effect on the resulting output. However, when the control parameter passes through a critical point or threshold in an intrinsically nonlinear system an abrupt change in the attractor can occur. This sensitive dependence on parameters is called a bifurcation in mathematics, or a nonequilibrium phase transition in physical theories of pattern formation (Haken 1977).

3. Concepts Of Self-Organization

Dynamical theory, by itself, does not give us any essential insights into how patterns of behavior may be created in complex systems that contain multiple (often different) elements interacting nonlinearly with each other and their environment. This is where the concept of self-organization is helpful (Haken 1977, Nicolis and Prigogine 1977).

Self-organization refers to the spontaneous formation of pattern and pattern change in complex systems whose elements adapt to the very patterns of behavior they create. Think of birds flocking, fish schooling, bees swarming. There is no ‘self ’ inside the system ordering the elements, dictating to them what to do and when to do it. Rather, the system, which includes the environment, literally organizes itself. Inevitably, when the elements form a coupled system with the world, coordinated patterns of behavior arise. Emergent pattern reflects the collective behavior of the elements. Collective behavior as a result of self-organization reduces the very large number of degrees of freedom into a much smaller set of relevant dynamical variables called, appropriately enough, collective variables. The enormous compression of degrees of freedom near critical points can arise because events occur on different timescales: the faster individual elements in the system may become ‘enslaved’ to the slower, emergent pattern or collective variables, and lose their status as relevant behavioral quantities (Haken 1977). Alternatively, one may conceive of a hierarchy of timescales for various processes underlying human behavior. On a given level of the hierarchy are pattern variables subject to constraints (e.g., of the task) that act as boundary conditions on the pattern dynamics. At the next level down are component processes and events that typically operate on faster timescales. Notice in this scheme (Kelso 1995), the key is to chose a level of description and understand the relation between adjacent levels, not reduce to some ‘fundamental’ lower level.

So what causes behavioral patterns to form? And what causes pattern change? It is here that the connection between processes of self-organization and dynamical systems theory becomes quite explicit. In complex systems that are open to exchanges of information with their environment, naturally occurring environmental conditions or intrinsic, endogenous factors may take the form of control parameters in a nonlinear dynamical system. When the control parameter crosses a critical value, instability occurs, leading to the formation of new (or different) patterns.

Dynamic instability is the generic mechanism underlying spontaneous self-organized pattern formation and change in all systems coupled to their internal or external environment. The reason is that near instability the individual elements, in order to adjust to current conditions (control parameter values), must order themselves in a new or different way. Fluctuations are always present, constantly testing whether a given behavioral pattern is stable. Fluctuations are not just noise; rather, they allow the system to discover new, more adaptive behavioral patterns.

The patterns that emerge and change near instabilities have a rich and highly nonlinear pattern, or coordination dynamics. Herein lies the basis of the hypothesis that human beings and the basic forms of behavior they produce, may be understood as self-organizing dynamical systems (Kelso 1995). Humans—complex systems consisting of multiple, interacting elements—produce behavioral patterns that are captured by collective variables. The resulting dynamical rules are essentially nonlinear and thus capable of producing a rich repertoire of behaviors. By this hypothesis, all human behavior—even human cognitive development (Magnusson 1995, Thelen and Smith 1994) and learning (Zanone and Kelso 1992) which occur on very different time scales—arises because complex material systems, through the process of self-organization, create a dynamic, pattern forming system that is capable of both behavioral simplicity (such as fixed point behavior) and enormous, even creative, behavioral complexity (such as chaotic behavior). No new principles, it seems, need be introduced (but see Sect. 5).

4. Finding Dynamical Laws In Behavioral And Social Systems

In the social and behavioral sciences the key collective variables characterizing the system’s state space are seldom known a priori and have to be identified. Science always needs special entry points, places where irrelevant details may be pruned away while retaining the essential aspects of the behavior one is trying to understand. Unique to the perspective of self-organized dynamical systems is its focus on qualitative change, places where behavior bifurcates. The reason is that qualitative change affords a clear distinction between one pattern and another, thereby enabling one to identify the key pattern variables that define behavioral states.

Likewise, any parameter that induces qualitative behavioral change qualifies as a control parameter. The payoff from knowing collective pattern variables and control parameters is high: they enable one to obtain the dynamical rules of behavior on a chosen level of description. By adopting the same strategy the next level down, the individual component dynamics may be studied and identified. It is the interaction between these that creates the patterns at the level above, thereby building a bridge across levels of description.

5. The Laws That Bind Us

It has long been recognized that social relationships are an emergent product of the process of interaction. Commonly studied relationships are the mother– infant interaction, the marriage bond and the patienttherapist relation, all of which are extremely complicated and difficult to understand. A more direct approach may be to study simpler kinds of social coordination, with the aim of determining whether such emergent behavior is self-organized, and if so what its dynamics are.

As an illustrative example, consider two people coordinating their movements. In this particular task each individual is instructed to oscillate a limb (the lower leg in this case) in the same or opposite direction to that of the other (Schmidt et al. 1990). Obviously the two people must watch each other in order to do the task. Then, either by an instruction from the experimenter or by following a metronome whose rate systematically increases, the social dyad also must speed up their movements.

When moving their legs up and down in the same direction, the two members of the dyad can remain synchronized throughout a broad range of speeds. However, when moving their legs in the opposite direction (one person’s leg extending at the knee while the other’s is flexing), such is not the case. Instead, at certain critical speeds participants spontaneously change their behavior so that the legs now move in the same direction.

How might these social coordination phenomena be explained? The pattern variable that changes qualitatively at the transition is the relative phase, φ. When the two people move in the same direction, they are in-phase with each other, φ = 0. When they move in different directions, their behavior is antiphase (φ = ± π radians or ± 180 degrees).

The phase relation is a good candidate for a collective variable because it clearly captures the spatiotemporal ordering between the two interacting components. Moreover, φ changes far more slowly than the variables that might describe the individual components (position, velocity, acceleration, electromyographic activity of contracting muscles, etc.) Importantly, φ changes abruptly at the transition.

The simplest dynamics that captures all the observed facts is

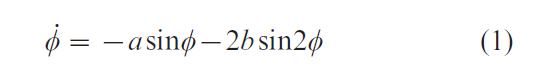
where φ is the relative phase between the movements of the two individuals, φ is the derivative of φ with respect to time, and the ratio b/a is a control parameter corresponding to the movement rate in the experiment. An equivalent formulation of Eqn. (1) is

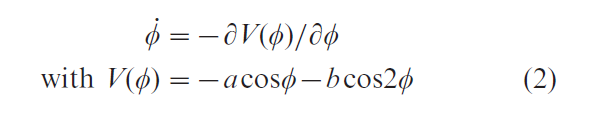
In the literature, this is called the HKB model of coordinated behavior, after Haken et al. (1985) who formulated it as an explanation of the coordination of limb movements within a single person (Kelso 1984). Figure 1 (top) allows one to develop an intuitive understanding of the behavior of Eqn. (2), as well as to connect to the key concepts of stability and instability in self-organizing dynamical systems introduced earlier. The dynamics can be visualized as a particle moving in a potential function, V(φ). The minima of the potential are points of vanishing force, giving rise to stable solutions of the HKB dynamics. As long as the speed parameter (b/a) is slow, meaning the cycle period is long, Eqn. (2) has two stable fixed point attractors, collective states at φ = 0 and φ = ± π rad. Thus, two coordinated behavioral patterns coexist for exactly the same parameter values, the essentially nonlinear feature of bistability. Such biand in general multistability is common throughout the behavioral and social sciences. Ambiguous figures (old woman or young girl? Faces or vase?) are well-known examples (e.g., Kruse and Stadler 1995).

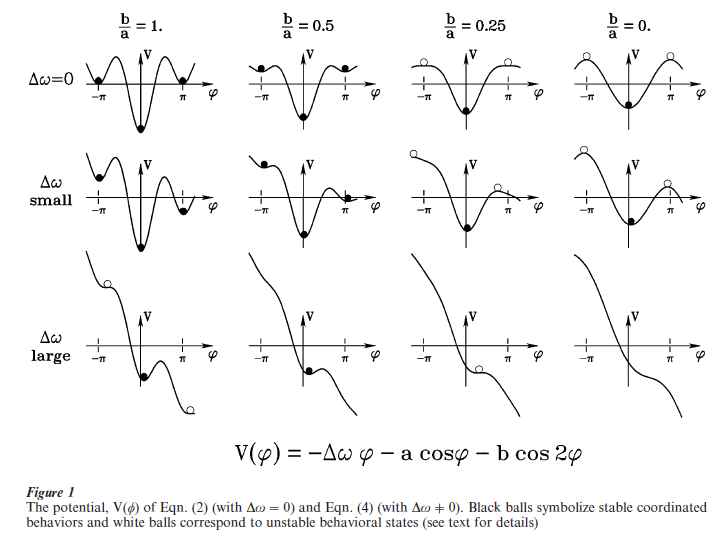
As the ratio b/a is decreased, meaning that the cycle period gets shorter as the legs speed up, the formerly stable fixed point at φ = ± π rad. becomes unstable, and turns into a repellor. Any small perturbation will now kick the system into the basin of attraction of the stable fixed point (behavioral pattern) at φ = 0. Notice also that once there, the system’s behavior will stay in the in-phase attractor, even if the direction of the control parameter is reversed. This is called hysteresis, a basic form of memory in nonlinear dynamical systems.

What about the individual components making up the social dyad? Research has established that these take the form of self-sustaining oscillators, archetypal of all time-dependent behavior whether regular or not. The particular functional form of the oscillator need not occupy the reader here. More important is the nature of the nonlinear coupling that produces the emergent coordination. The simplest, perhaps fundamental coupling that guarantees all the observed emergent properties of coordinated behavioral patterns—multistability, flexible switching among behavioral states, and primitive memory, is

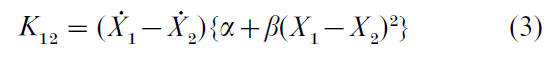
where X₁ and X₂ are the individual components and α and β are coupling parameters. Notice that the ‘next level up,’ the level of behavioral patterns and the dynamical rule that governs them (Eqns.(1) and (2)), can be derived from the level below, the individual components and their nonlinear interaction. One may call this constructive reductionism: by focusing on adjacent levels, under the task constraint of interpersonal coordination, the individual parts can be put together to create the behavior of the whole.

The basic self-organized dynamics, Eqns. (2) and (3) have been extended in numerous ways, only a few of which are mentioned here.

(a) Critical slowing down and enhancement of fluctuations. Introducing stochastic forces into Eqns. (1) and (2) allows key predictions to be tested and quantitatively evaluated. Critical slowing is easy to understand from Fig. 1 (top). As the minima at φ = ± π become shallower and shallower, the time it takes to adjust to a small perturbation takes longer and longer. Thus, the local relaxation time is predicted to increase as the instability is approached because the restoring force (given as the gradient in the potential) becomes smaller. Likewise, the variability of φ is predicted to increase due to the flattening of the potential near the transition point. Both predictions have been confirmed in a wide variety of experimental systems, including recordings of the human brain.

(b) Symmetry breaking. Notice that Eqns. (1) and (2) are symmetric: the dynamical system is 2π periodic and is identical under left-right reflection (φ is the same as – φ). This assumes that the individual components are identical, which is seldom, if ever the case. Nature thrives on broken symmetry. To accommodate this fact, a term ∆ω is incorporated into the dynamics

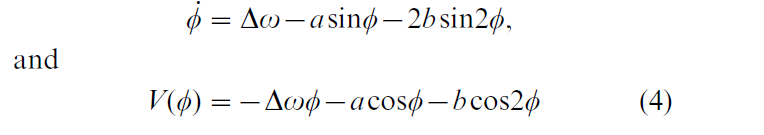
for the equation of motion and the potential respectively. Small values of ∆ω shift the attractive fixed points (Fig. 1 middle) in an adaptive manner. For larger values of ∆ω the attractors disappear entirely (Fig. 1 bottom) causing the relative phase to drift: no coordination between the components occurs. Note, however, that the dynamics still retain some curvature (Fig. 1 bottom right): even though there are no attractors there is still attraction to where the attractors used to be. The reason is that the difference (∆ω) between the individual components is sufficiently large that they do their own thing, while still retaining a tendency to cooperate. This is how global integration, in which the component parts are locked together, is reconciled with the tendency of the parts to function locally, as individual autonomous units (Kelso 1995).

(c) Information: a new principle? Unlike the behavior of inanimate things, the self-organizing dynamics of human behavior is fundamentally informational, though not in the standard sense of data communicated across a channel (Shannon and Weaver 1949). Rather, collective variables are context-dependent and intrinsically meaningful. Context-dependence does not imply lack of reproducibility. Nor does it mean that every new context requires a new collective variable or order parameter. As noted above, within and between-person coordinated behaviors are described by exactly the same self-organizing dynamics. One of the consequences of identifying the latter is that in order to modify or change the system’s behavior, any new information (say a task to be learned, an intention to change one’s behavior) must be expressed in terms of parameters acting on system-relevant collective variables. The benefit of identifying the latter is that one knows what to modify. Likewise, the collective variable dynamics—prior to the introduction of new information—influences how that information is used. Thus, information is not lying out there as mere data: information is meaningful to the extent that it modifies, and is modified by, the collective variable dynamics.

(d) Generalization. The basic dynamics (Eqns. (1–4)) can readily be elaborated as a model of emergent coordinated behavior among many anatomically different components. Self-organized behavioral patterns such as singing in a group or making a ‘wave’ during a football game are common, yet unstudied examples. Recently, Neda et al. (2000) have examined a simpler group activity: applause in theater and opera audiences in Romania and Hungary. After an exceptional performance, initially thunderous incoherent clapping gives way to slower, synchronized clapping. Measurements indicate that the clapping period suddenly doubles at the onset of the synchronized phase, and slowly decreases as synchronization is lost. This pattern is a cultural phenomenon in many parts of Europe: a collective request for an encore. Increasing frequency (decreasing period) is a measure of the urgency of the message, and culminates in the transition back to noise when the performers reappear. These results are readily explained by a model of a group of globally coupled nonlinear oscillators (Kuramoto 1984)

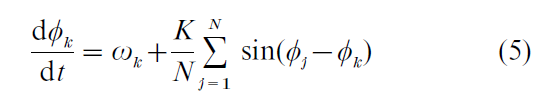
in which a critical coupling parameter, K_c determines the different modes of clapping behavior. K is a function of the dispersion (D) of clapping frequencies

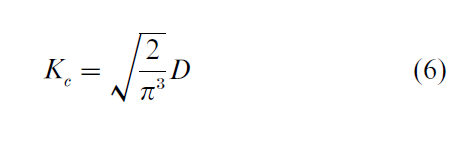
During fast clapping, synchronization is not possible due to the large dispersion of clapping frequencies. Slower, synchronized clapping at double the period arises when small dispersion appears. Period doubling rhythmic applause tends not to occur in big open-air concerts where the informational coupling among the audience is small. K can also be societally imposed. In Eastern European communities during communist times, synchronization was seldom destroyed because enthusiasm was often low for the ‘great leader’s’ speech. For people in the West, the cultural information content of different clapping patterns may be quite different. Regardless, the mathematical descriptions for coordinated behavior—of social dyads and the psychology of the crowd—are remarkably similar.

6. Conclusion And Future Directions

The theoretical concepts and methods of self-organizing dynamics are likely to play an ever greater role in the social, behavioral, and cognitive sciences, especially as the interactions among disciplines continues to grow. Up to now, the use of nonlinear dynamics is still quite restricted, and largely metaphorical. One reason is that the tools are difficult to learn, and require a degree of mathematical sophistication. Their implementation in real systems is nontrivial, requiring a different approach to experimentation and observation. Another reason is that the dynamical perspective is often cast in opposition to more conventional theoretical approaches, instead of as an aid to understanding. The former tends to emphasize decentralization, collective decision-making and cooperative behavior among many interacting elements. The latter tends to focus on individual psychological processes such as intention, perception, attention, memory, and so forth. Yet there is increasing evidence that intending, perceiving, attending, deciding, emoting, and remembering have a dynamics as well. The language of dynamics serves to bridge individual and group processes. In each case, dynamics must be filled with content, with key variables and parameters obtained for the system under study. Every system is different, but what we learn about one may aid in understanding another. What may be most important are the principles and insights gained when human brains and human behavior are seen in the light of self-organizing dynamics.

Bibliography:

1. Abraham R H, Shaw C D 1982 Dynamics: The Geometry of Behavior. Ariel Press, Santa Cruz, CA
2. Arbib M A, Erdi P, Szentagothai J 1998 Neural Organization: Structure, Function and Dynamics. MIT Press, Cambridge, MA
3. Haken H 1977 Synergetics, an Introduction: Non-equilibrium Phase Transitions and Self-organization in Physics, Chemistry and Biology. Springer, Berlin
4. Haken H 1996 Principles of Brain Functioning. Springer, Berlin
5. Haken H, Kelso J A S, Bunz H 1985 A theoretical model of phase transitions in human hand movements. Biological Cybernetics 51: 347–56
6. Kelso J A S 1984 Phase transitions and critical behavior in human bimanual coordination. American Journal of Physiology: Regulatory, Integrative and Comparative 15: R1000–4
7. Kelso J A S 1995 Dynamic Patterns: The Self-organization of Brain and Behavior. MIT Press, Cambridge, MA
8. Kelso J A S, Fuchs A 1995 Self-organizing dynamics of the human brain: Critical instabilities and Sil’nikov chaos. Chaos 5(1): 64–9
9. Kuramoto Y 1984 Chemical Oscillations, Waves and Turbulence. Springer-Verlag, Berlin
10. Magnusson D 1995 Individual development: A holistic, integrated model. In: Moen P, Elder G H Jr, Luscher K (eds.) Examining Lives in Context. American Psychological Association, Washington, DC
11. Mandelbrot B 1982 The Fractal Geometry of Nature. Freeman, New York
12. Neda Z, Ravasz E, Brechet Y, Vicsek T, Barabasi A L 2000 The sound of many hands clapping. Nature 403: 849–50
13. Nicolis G, Prigogine I 1977 Self-organization in Nonequilibrium Systems. Wiley, New York
14. Port R F, van Gelder T 1995 Mind as Motion: Explorations in the Dynamics of Cognition. MIT Press, Cambridge, MA
15. Saltzman E L, Kelso J A S 1987 Skilled actions: A task dynamic approach. Psychological Review 94: 84–106
16. Schmidt R C, Carello C, Turvey M T 1990 Phase transitions and critical fluctuations in the visual coordination of rhythmic movements between people. Journal of Experimental Psychology: Human Perception and Performance 16: 227–47
17. Shannon C E, Weaver W 1949 The Mathematical Theory of Communication. University of Illinois Press, Chicago
18. Strogatz S H 1994 Nonlinear Dynamics and Chaos. AddisonWesley, Reading, MA
19. Thelen E, Smith L B 1994 A Dynamic Systems Approach to the Development of Cognition and Action. MIT Press, Cambridge, MA
20. Vallacher R R, Nowak A 1997 The emergence of dynamical social psychology. Psychological Inquiry 8: 73–99
21. Van Geert P 1995 Learning and development: A semantic and mathematical analysis. Human Development 38: 123–45
22. Zanone P G, Kelso J A S 1992 The evolution of behavioral attractors with learning: Nonequilibrium phase transitions. Journal of Experimental Psychology: Human Perception and Performance 18/2: 403–21