Sample Probabilistic Thinking Research Paper. Browse other research paper examples and check the list of research paper topics for more inspiration. If you need a religion research paper written according to all the academic standards, you can always turn to our experienced writers for help. This is how your paper can get an A! Feel free to contact our research paper writing service for professional assistance. We offer high-quality assignments for reasonable rates.
1. Introduction
Some people have enjoyed playing games that involved at least a component of chance ever since civilizations—as we know them—emerged in human history. Many of these people apparently had a fairly good intuitive idea of what we might now term the ‘probabilities’ or ‘odds’ of various outcomes associated with these games. Alternatively, at least some people (whom in hindsight we might now label ‘superstitious’) believed that the outcomes of these games could indicate something about the favorability of the world in general toward the gambler (a belief that may exist even today—at least on an implicit basis—for chronic gamblers), specifically the favorability or unfavorability of a particular god that was involved with a particular game.
Academic Writing, Editing, Proofreading, And Problem Solving Services
Get 10% OFF with 24START discount code
In the last 600 years or so people have proposed systematic ways of evaluating probabilities—e.g., in terms of equally likely outcomes in games of chance or in terms of subjective belief. In the last 150 years or so scientific endeavor has started to make specific use of probabilistic thinking, and in the last 100 years or so probabilistic ideas have been applied to problems of everyday life. (see Gigerenzer et al. 1989). Currently, for example, jurors are often asked to determine manufacturer or company liability on the basis of differential rates of accidents or cancers; in such judgments, jurors cannot rely on deterministic reasoning that would lead to a specification of exactly which negative outcome is due to what; nor can they rely on ‘experience’ in these contexts in which they have had none. Thus, it is extraordinarily important to understand—if indeed generalizations about such thinking are possible—how it is that people think about and evaluate probabilities, and in particular the problems that they (we) have. The major thesis presented here is that both the thinking and the problems can be understood in terms of systematic deviations from the normative principles of probabilistic reasoning that have been devised over the past five or so centuries. These deviations are not inevitable; it is certainly possible for people to think about probabilities coherently (at least on occasion); nevertheless, when deviations occur, they tend to be of the systematic nature to be described here; they occur most often when people are engaged in what is termed ‘automatic’ or ‘associational’ thinking, as opposed to ‘reflective’ and ‘comparative’ thinking. (These terms will be made more precise later in this research paper.)
2. A Brief History (Of Thought)
Beginning in early infancy, we develop intuitions about space, time, and number (at least to the extent of ‘one, two, three, many’). These intuitions are essentially correct. They remain throughout our lives basically unaltered except for small variations, and they form the foundation of far more sophisticated mathematical systems that have been developed over the past thousands of years. Moreover, their importance in our lives has been clear throughout those millennia.
In contrast, probabilistic thinking is often unintuitive, and it generally can be taught only after we are familiar with fractions, so that analogs to relative frequency are clear. Moreover, our intuitions about probabilities are often just plain wrong. For example, belief in the ‘gambler’s fallacy’ (negative recency) can even be explicitly rejected, but nevertheless implicitly influence decision making—such as when people demand a greater amount of money in preference to gambling on an outcome that is ‘due’ (e.g., a tail after five straight heads) than in preference to gambling on one that isn’t (e.g., an additional head); see Gold (1997).
The fairly recent, and somewhat ‘iffy,’ use of probabilistic judgment does not imply, however, that people did not gamble throughout the centuries. As mentioned previously, the outcomes of games of chance could provide not just monetary winners and losers but ‘signals’ from ‘the gods’ about favorability toward the gambler; this belief is well captured by the narrative of the novelist Robert Graves (1943) about Caligula’s gambling shortly before his assassination. This tyrant is both watching gladiator games, often putting to death people he has bribed to lose, and rolling a form of dice called ‘astragali’—which are four-sided dice made from pig or lamb bones.
Caligula is playing with his Uncle Claudius, who in order to avoid winning (a dangerous outcome for Claudius) hands the emperor beautiful new dice loaded to come up with a ‘Venus roll,’ which consists of four separate sides (generally with the numbers 1, 3, 4, and 6). Caligula’s subsequent success convinces him that Venus is favorable toward him that day, and he does not take the usual precautions upon leaving the games. Throughout his life, Claudius feels guilty that the loaded dice sent the wrong message to Caligula about how Venus felt about him that day—an inappropriate intervention between a god and a man. (According to Hacking 1975, the interpretation of such events as ‘signals’ from ‘on high’ is common up to the Renaissance, even after people in Europe had given up polytheism for monotheism; the reader might also note how often in the Old Testament people decide to ‘cast lots’ to decide what to do—apparently in the belief that God would determine the outcome.)
Of course, not everyone believed in such intervention. For example, Cicero is quoted as claming that ‘Nothing is so unpredictable as a throw of the dice [modern translation],’ and that ‘both now and then indeed he will make it [the Venus roll] twice and even thrice in succession. Are we going to be so feebleminded then as to aver that such a thing happened by the personal intervention of Venus rather than by pure luck?’ (see David 1962, p. 25).
Among those not so superstitious (such as Cicero, who was himself assassinated), the intuitive understanding gained through experience of which bets are good ones and which bets are bad ones led to fairly good implicit estimates of probability. Even now, however, Wagenaar (1988) finds chronic gamblers to be more reliant on intuition and experience than on mathematical analysis.
In contrast, explicit probabilistic thinking goes beyond experience. We can, for example, indicate what are good or bad bets in gambles we have just now constructed, with which we have had no previous experience. Probabilistic thinking can also be extended to ‘personal belief’ about uncertain events, it can be used to evaluate risks, and it can serve as a guide for social policy.
Systematic, probabilistic thinking appears to have started with questions about gambling (in particular about gambles that have not yet been played multiple times). Despite the fact that people gambled a lot, however, the formal theory did not begin until the Italian Renaissance, specifically in correspondence and argumentation between Geronimo Cardano (1501–76) and his associates. The approach that has been ascribed to Cardano involved Comparative rather than associational thinking. He proposed that the likelihood of success of a gamble could be computed, or at least approximated, by comparing the number of outcomes of the device favorable to the gambler divided by the total number of outcomes. In situations where the gambling device is set up to make each possible outcome equally likely, this ratio assessment of probability is used today. The ratio assessment leads to certain general principles, often termed ‘axioms,’ which in turn provide a more abstract notion of probability, and allow different interpretations of probability to be developed—just provided they lead to measures consistent with the axioms. For example, Ramsey (1931) demonstrated that when explicit probabilities are used to determine fair gambling odds, then the gambler will follow the basic principles of probability theory if and only if it is not possible to make a ‘Dutch Book’ (see de Finetti 1974–5, p. 87) such that the gambler always loses; that is, the gambler will be consistent if and only if it is impossible for a highly intelligent opponent to make a series of bets such that the opponent always wins.
After Cardano, the idea of probabilistic inference developed quite rapidly. Many French and Dutch intellectuals corresponded with each other about what constituted better or worse bets—not just in games that had been played chronically, but in games of their own invention. Interestingly, when they discussed probability, they often did so in terms of the expected value of the game, and questions were often posed as to which of the two games had a higher expected value. Then there was rapid development of probability theory—for example, Bernoulli’s’ Law of Large Numbers,’ which specified the relationship between the probability of a single outcome and the probability distribution of multiple outcomes of the same type (for example, the relationship between the probability a fair coin comes up heads and the probability that it comes up heads at least three times in 10 trials); the ‘law’ itself derived the limit of the proportion of heads as the number of trials becomes indefinitely large. To jump ahead to recent times, von Neumann and Morgenstern published their classic work Theory of Games and Economic Behavior (1944 1947), in which again the question was one of choosing between different gambles, but in terms of expected utility rather than expected value. This work was quite consistent with the earliest work, in which the question of probability was secondary to the question of choice between alternative courses of action.
3. Probability Assessments
All probabilistic analysis is based on the idea that (suitably trained and intelligent) people can at least recognize good probabilistic arguments presented by someone else, or discovered or thought of by themselves, but not necessarily generate good assessments. The very fact that there was correspondence about the gambles—and occasionally some disputes about them—indicated that people do not automatically assess probabilities in the same way, or accurately (e.g., corresponding to relative frequencies, or making good gambling choices).
The von Neumann and Morgenstern work, however, does involve some psychological assumptions that people can engage in ‘good’ probabilistic thinking. First, they must do so implicitly, so that the choice follows certain ‘choice axioms’ that allow the construction of an expected utility model—i.e., a model that represents choice as a maximization of implicit expected utility; that in turn requires that probabilities at the very least follow the standard axioms of probability theory. It also implies considering conditional probabilities in a rational manner, which is done only when implicit or explicit conditional probabilities are consistent with Bayes’ theorem. Thus, the von Neumann and Morgenstern work required that people be ‘Bayesian’ in a consistency sense, although that term is sometimes used to imply that probabilities should at base be interpreted as degrees of belief. Another way in which probability assessment must be ‘good’ is that there should be some at least reasonable approximation between probabilities and long-term relative frequencies; in fact, under particular circumstances (of interchangeability and indefinitely repeated observations), the probabilities of someone whose belief is constrained by Bayes’ theorem must approximate relative frequencies (Dawid 1982).
Are people always coherent? Consider an analogy with swimming. People do swim well, but occasionally we drown. What happens is that there is particular systematic bias in attempting to swim that makes it difficult. We want to hold our heads above water. When, however, we raise our heads to do so, we tend to assume a vertical position in the water, which is one of the few ways of drowning (aside from freezing or exhaustion or being swept away in rough waters).
Just as people drown occasionally by trying to hold their heads above water, people systematically deviate from the rules of probabilistic thinking. Again, however, the emphasis is on ‘systematic.’ For example, there is now evidence that people’s probabilistic judgments are ‘subadditive’—in that when a general class is broken into components, the judgmentally estimated probabilities assigned to disjoint components that comprise the class sum to a larger number than the probability assigned to the class. That is particularly true in memory, where, for example, people may recall the frequency with which they were angry at a close friend or relative in the last month and the frequency with which they were angry at a total stranger, and the sum of the estimates is greater than an independent estimate of being angry period (even though it is possible to be angry at someone who is neither a close friend or relative nor a total stranger; see Mulford and Dawes 1999). The clever opponent will then bet against the occurrence of each component but on the occurrence of the basic event, thereby creating a Dutch Book.
4. The Heuristics And Biases Approach To Problems Of Probabilistic Thinking
The basic conception is that we all use a series of ‘heuristics’ in our everyday estimation (explicit or implicit) of probabilities, and these heuristics lead to biases. These heuristics provide a type of ‘bounded rationality’ (Simon 1955, 1956, 1979)—in that they substitute for a very detailed or logical analysis, an analysis that may be beyond our ‘computational capacity.’ Just as associational thinking serves us well in many contexts, however, so do the heuristics. Occasionally, however, they lead to grossly erroneous—systematically erroneous—probabilistic thinking. The conception that heuristics have some type of ‘generalized validity,’ but that they often lead us astray, was well argued in a classic Science article by Tversky and Kahneman (1974); unfortunately, the principle has been lost on some critics, who can point out many situations in which these heuristics ‘work.’ Naturally, they do. If they didn’t have some sort of generalized utility, they would not have survived over generations of people trying to make probabilistic judgments.
One of the most important of these heuristics is termed the ‘representativeness’ heuristic, which was first proposed by Tversky and Kahneman in an article concerning Belief in the Law of Small Numbers (1971). The idea supported in that article is that we expect very small samples to ‘represent’ the populations from which they were drawn, where the ‘we’ includes even people with a fair amount of formal training in statistics. That expectation leads to judgment of probability on the basis of the degree to which an instance or a sample matches a population or general idea, rather than on a judgment of how it can be generated. For example, when tossing a coin, a result consisting of six heads appears to be much less likely than one of a head followed by two tails, followed by two heads and finally a tail. But of course each of the sequences is equally likely; each occurs with probability 1 64. In fact, the sequence of a head followed by two tails followed by two heads and a tail is seen as more likely than a sequence of strict alternation of heads and tails—even though in general people believe that there is more than a chance amount of alternation when they judge what is truly ‘random’ (and in fact are most apt to pick as random the sequence that has a transition probability of 2/3 rather than 1/2). This incorrect expectation of alternation leads to such erroneous beliefs as that in the ‘hot hand’ in basketball when observing clusters of similar outcomes (e.g., successful shots). See, for example, Gilovich et al. (1985).
Another heuristic is termed an availability one. Briefly, we estimate frequencies on the ease with which instances ‘come to mind,’ or on our judgment of the ease with which we can recall or generate instances. It is, in fact, generally true that when there are more instances as opposed to fewer in the world, we find it easier to recall or generate more as opposed to fewer. The problem is, however, that there are determinants of ease of recall or generation that are independent of—or sometimes even in conflict with—actual relative frequency in our environment. For example, vivid instances are more readily recalled than pallid ones. (See again the result on ‘subadditivity’ in memory.) Moreover, instances that are easily imaginable (even if we haven’t actually experienced them) are more readily ‘brought to mind’ than are those difficult to imagine.
The availability heuristic creates a bias when we are unaware of the factors other than frequency that can result in ease of recall or generation, but use it as a way of estimating actual frequency. Sometimes, the bias is so strong that we even ignore instances that we cannot sample—a ‘structural availability’ problem. For example, clinical psychologists often claim that no child sexual abusers stop on their own without therapy. When asked to substantiate this claim, they will cite many of the child abusers with whom they have had contact, often mandated by a judge to enter therapy with them. The problem is, however, that they would not have had contact with any who had stopped on their own, and by definition they were seeing people only in a therapy setting, hence could not observe any of them stopping ‘without therapy.’ Nevertheless, the experience with such people is so salient and compelling that even while acknowledging the logical problem with the conclusion, many of these clinical psychologists simply revert to the belief a day or a week after having publicly recognized the availability bias (see Dawes 1988, p. 102).
Following the ideas of Fischhoff and Beyth-Marom (1983) as elaborated by Dawes (1998), the standard cognitive biases and heuristics can be understood by alluding to simple forms of Bayes’ theorem. Consider, for example, the relationship between a symptom S and a disease D, and suppose a diagnostician observes this symptom S. If the probability of the disease is assessed on the basis of a pure matching or association between the symptom and the disease, independent of considerations of conditional probability, there is no normative structure to which the judgment corresponds. More often, however, the judgment will be made on the basis of the conditional probabilities—a normatively correct judgment if it is based on the conditional probability of the disease given the symptom, P(D/S), but a representative judgment if it is the probability of the symptom given the disease, P(S/D). Unfortunately, there is a lot of evidence that the judgment is often made on the basis of the latter relationship—when conditional probabilities are considered at all.
The relationship between these two probabilities is given by rewriting Bayes’ theorem as:
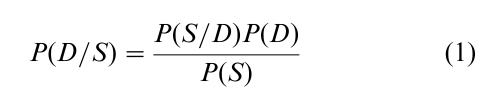
It can also be written in terms of the ‘ratio rule’:
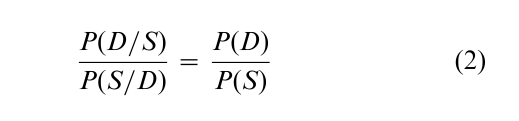
Because the ratio rule follows from the very definition of conditional probability, it is simply incoherent to equate the probability of the disease given the symptom with the probability of the symptom given the disease in the absence of a simultaneous belief that the probability of the disease and the probability of the symptom are identical. (Again, if someone were to make a series of bets based on ‘fair betting odds’ in such a belief, an opponent could make a Dutch Book against that person.) Classic representative thinking—e.g., ‘she gave a typical schizophrenic response, therefore she must be schizophrenic’—embraces such an identity. What is critical, of course, are the base rates of D and of S, yet extensive research has shown that people underutilize such base rates in their intuitive judgments—or at least fail to incorporate them to a sufficient extent into their prior beliefs, given that they are often seen as ‘not relevant.’ (Why, people often ask, should the general probabilities of these symptoms and diseases be relevant to a particular judgment about a particular person with a particular symptom? Such an argument is sometimes even followed by bland assertions to the effect that ‘statistics do not apply to the individual’—a wholly erroneous conclusion, as can be attested to by the heavy cigarette smoker who develops lung cancer.)
People often do not ignore these base rates entirely in the judgments, particularly if the probabilistic nature of the judgment is made clear (see Gigerenzer et al. 1989). Nevertheless, the ‘underutilization’ of such base rates is ubiquitous. In the psychological literature it was first decried by Meehl and Rosen (1955), who noted that in case conferences they attended, clinical psychology and psychiatry judges tended to ignore base rates completely; later, underutilization has been established in a variety of experimental situations using a wide variety of subjects, especially by Kahneman and Tversky (1972, 1973). For example, when asked to judge whether a description is of a particular engineer or a particular lawyer, subjects make the same judgment whether the experimenter states that the description was drawn from a pool of 70 percent engineers and 30 percent lawyers, or vice versa. As Bar-Hillel (1990) points out, the 70/30 split does not appear to be ‘relevant,’ but it’s relevance would most likely be clear if the split were 99/1, and certainly if it were a 100/0. (Again, we can hypothesize that people can recognize probabilistic arguments— although it’s possible to be fooled on occasion—but often not make them spontaneously.) Thus, for example, someone who is said to be interested in sailing and carpentry and sharing model train sets with a child is judged to be much more likely to be an engineer than a lawyer, whether this person was drawn from a pool of 70 percent engineers or 70 percent lawyers. Making the sampling procedure absolutely ‘transparent’ does, however, reduce that tendency.
The use of Bayes’ theorem to understand the relationship between symptoms and disease leads naturally to its use to consider the general relationship between any hypotheses and any bit of evidence. Let e refer to some bit of evidence about whether a hypothesis h is or is not true; for example, a symptom may be regarded as a bit of evidence, and having a particular disease a hypothesis; or the hypothesis may concern who is going to win the election in the United States in the year 2020 and a particular bit of evidence may be the margin of victory or defeat of the potential candidate in a more local election. Bayes’ theorem expressed in terms of evidence and hypotheses is presented as
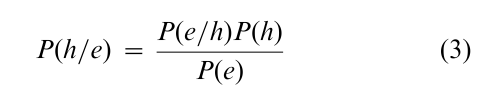
This form of Bayes’ theorem, while true, often leads to complications when trying to evaluate the probability of the evidence. There is, however, a way to avoid having to estimate that probability. What we can do is to consider odds that the hypothesis is true. These odds are the probability the hypothesis is true given the evidence divided by the probability that this hypothesis is false given the evidence—that is, by the ratio P(h/e) P(–h/e). Once we know the odds, it is trivial to compute the probability. The advantage of considering odds is that the denominator in Bayes’ theorem cancels out when we compute these odds. That is
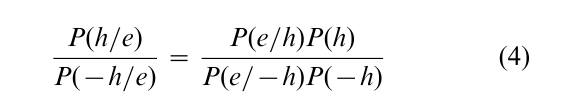
Now we are in a position to categorize the most common forms of representative thinking. Pseudodiagnosticity refers to making an inference about the validity of hypothesis h on the base of evidence e without considering hypothesis –h. Another way of stating pseudodiagnosticity is that it involves considering only the numerator of the first term on the right-hand side in Eqn. (4). People do that when they state that a bit of evidence is ‘consistent with’ or ‘typical of’ some hypothesis without concerning themselves about alternative hypotheses, or in particular the negation of the hypothesis. For example, in attempting to diagnose whether a child has been sexually abused, alleged experts in court often refer to symptoms ‘typical’ of such abuse—without concerning themselves with how typical these symptoms are of children who have not been abused, or the frequency with which children have been sexually abused.
Another type of representative thinking involves considering the probability of the evidence given the hypothesis or hypotheses without looking at the second terms in Eqn. (4), that is, the prior odds. The reason that these odds are important is that they yield the extent of the evidence and hypotheses considered. For example, being a poor speller may be evidence of dyslexia in the sense that it has a very high probability given dyslexia. However, in order to diagnose dyslexia on the basis of poor spelling, we have to know something about the base rates of poor spelling and the base rates of dyslexia in the population from which the person whom we wish to diagnose was chosen.
Dilution effects occur when evidence that does not distinguish between hypotheses in fact influences people to be less convinced of a most likely hypothesis; the problem is similar to that found in pseudodiagnosticity in that people do not realize that evidence that is not very likely given the hypothesis may be equally unlikely given the negation of that hypothesis, but may in fact believe a hypothesis less as a result of collecting evidence that is unlikely if it is true. Dilution is simply the converse of pseudodiagnosticity.
Finally, it is possible to describe a ailability biases as well by Eqn. (4). People believe that they are sampling evidence given the hypothesis, when in fact they are sampling this evidence given the hypothesis combined with the manner in which they are sampling. For example, when private practice clinical psychologists claim that they are sampling characteristics of people who fall into a certain diagnostic category on the basis of their experience, what they are really sampling is people who fall in that category and who come to them. Similarly, when we sample our beliefs about ‘what drug addicts are like,’ most of us are sampling on the basis of how the media presents drug addicts—both in ‘news’ programs and in dramatizations (Dawes 1994b). Doctors often sample on the basis of their contact with addicts when these addicts are ill, perhaps gravely so, while police are often sampling on the basis of their experience with these same addicts during arrests and other types of confrontation. It is not surprising, then, that doctors are in favor of a ‘medical’ approach to drug addiction including such policies as sterile needle exchanges, while police are in favor of much more punitive policies. Both are sampling evidence combined with their exposure to it.
All these anomalies have been demonstrated experimentally. It is important to point out, however, that the investigation of these anomalies did not spring simply from understanding Bayes’ theorem and then from creating very clever experimental situations in which subjects’ inferences systematically violate it. The motive to study these anomalies of judgment arises from having observed them on a more informal basis outside the experimental setting—and trying to construct an experimental setting, which yields a greater measure of control, that will allow them to be investigated in a systematic manner. The reader is referred, for example, to the essay of Meehl (1977) or the book of Dawes (1994a) for descriptions of these biases in the clinical judgment of professional psychologists and psychiatrists who rely on their own ‘experience’ rather than (dry, impersonal) ‘scientific’ principles for diagnosis and treatment.
5. Analyzing An Important Example
This section ends with a discussion of pseudodiagnosticity, a bias that is prevalent in ‘expert’ proclamations encouraging ‘child sex abuse hysteria’ (Dawes 2001). The main problem here is that hypotheses are not compared: instead, single hypotheses are evaluated in terms of the degree to which evidence is ‘consistent with’ them; in addition, evidence is often sought in terms of its consistency with or inconsistency with ‘favorite hypotheses’—rather than in terms of its ability to distinguish between hypotheses. This type of pseudodiagnosticity has made its way into the legal system, where experts are allowed to testify that a child’s recanting of a report of sexual abuse is ‘consistent with’ the ‘child sexual abuse accommodation syndrome’ (Summit 1983). The finding is that many children who are known to have been sexually abused deny the abuse later (recant), therefore, the probability of the evidence (the child recants) given the hypothesis (actual abuse) is not as low as might be naively assumed; therefore, recanting is ‘consistent with’ having been abused (i.e., can be considered part of a ‘syndrome’ of accommodation to abuse).
The problem with this pseudodiagnostic reasoning is that it compares the probability of the evidence given the hypothesis to the probability of the negation of the evidence given the hypothesis, whereas a rational comparison is of the probability of the evidence given the hypothesis to the probability of the evidence given the negation of the hypothesis. When considering this latter comparison, we understand immediately that the recanting would be diagnostic of actual abuse only if the probability of recanting given actual abuse were higher than the probability of recanting given such abuse had not occurred—a highly implausible (not to mention paradoxical) conclusion.
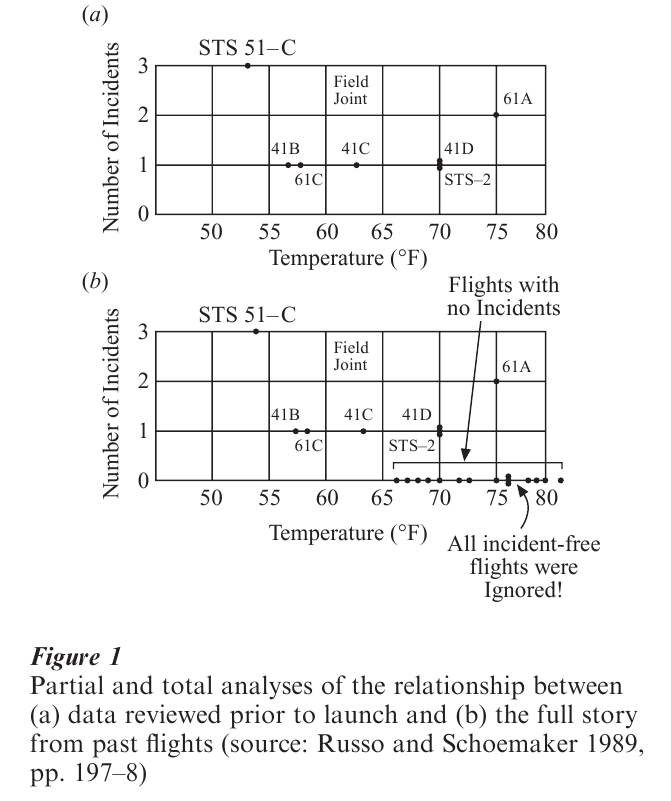
Such pseudodiagnostic reasoning is involved in other disasters as well, for example, the explosion of the US Space Shuttle Challenger on January 22, 1986. When considering the possibility that cold temperatures might cause the O-rings to malfunction, ‘the worried engineers were asked to graph the temperatures at launch time for the flights in which problems have occurred’ (Russo and Schoemaker 1989, p. 197). Thus, these engineers attempted to evaluate the hypothesis that there would be O-ring problems by asking what the temperature was given the existence of these problems. As indicated in Fig. 1(a) (Fig. 6 in Russo and Schoemaker 1989, p. 198), there appeared to be no relationship. When, however, the temperature of launches in which there were no problems were considered, a very clear relationship between problems and temperature is evident (see Fig. 1(b), from Russo and Schoemaker 1989, Fig. 7, p. 198.)
Moreover, people actively seek evidence compatible or incompatible with a hypothesis rather than evidence that distinguishes between hypotheses, as has been extensively studied by Doherty and his colleagues (see for example Doherty et al. 1979). Consider, for example, subjects who are asked to play the role of medical students (and actual medical students prior to specific training, see Wolf et al. 1985) who must determine whether patients have one of two conditions. The conditions are explained, and subjects are told that a patient has two symptoms. The judges are then presented with the conditional probability of one of these symptoms given one of the diseases (e.g., that it is very likely that the patient has a high fever given the patient has meningitis). They can then choose to find out the probability of the other symptom given the same disease, the probability of the first symptom given the second disease, or the probability of the second symptom given the second disease. While virtually no subjects choose a different symptom and a different disease, the majority choose to find the probability of the second symptom given the first disease (the ‘one that is focal’ as a result of being told the first symptom). But for all these subjects know, of course, the first symptom may be more or less typical of the alternative disease, as may the second symptom. Finding out that the probability of these two symptoms given only one disease in no way helps to distinguish between that disease and some other. Of course, in real medical settings doctors may ha e prior knowledge of these other disease symptom relationships, but because the diseases are not even identified in the current setting, such knowledge would be of no help.
Occasionally, pseudodiagnosticity has been confused with what has been termed a ‘confirmation bias’—that is, a desire to search for evidence that is very probable given a focal hypothesis. As Fischhoff and Beyth-Marom (1983), Trope and Bassok (1982), and Skov and Sherman (1986) point out, however, such a search does not necessarily imply pseudodiagnosticity (or any other particular irrationality) because it may be possible that the evidence is not found—that is, that instead of finding the anticipated evidence, the diagnostician finds its negation. In fact, Skov and Sherman (1986) demonstrate that in searching for evidence—at least in their experimental context—subjects often became quite rational when they are informed of the conditional probabilities. The irrationality occurs in the search for which probabilities to seek, and in ‘jumping’ to a conclusion on the basis of only one probability (i.e., on the basis of the first term in the numerator in the odds form of Bayes’ theorem).
The cognitive explanation of pseudodiagnosticity and the other heuristic-based biases covered in the section is simple. People often think by association; in fact, whole computer programs have been built to simulate human judgment on the basis of ‘matching’ characteristics to schemas. The point of pseudodiagnosticity is that only one ‘schema’ (i.e., hypothesis) is considered, whereas coherent diagnostic judgment is always Comparative. In fact, all the biases covered here are based on associational thinking, whereas clear normative probabilistic thinking always involves comparisons.
6. Summary And Implications
When we deal with probabilistic situations in everyday life, we can often ‘muddle through,’ but occasionally not appreciating the comparative nature of valid probabilistic thinking can lead to judgmental disasters. Similarly, experience with games of chance can lead to some pretty good intuitive estimations of the likelihood of various payoffs, but once again there can be systematic biases, such as belief in the gambler’s fallacy. Explicit probabilistic thinking has developed in our cultures only in the last 500 years or so, and in the last 150 years or so it has become increasingly important in both scientific reasoning and in our dayto-day living—and even in legal contexts (where as jurors we may be asked to judge the liability of a particular company by comparing the probability of developing cancer among those exposed to it or its product as opposed to the ‘base rate’ probability, or may be asked to evaluate what an expert witness states about the relationship between a symptom and a diagnosis). Here, if we rely on our intuitive grasp of probabilities, we often find that we have systematic biases, much as novice swimmers may attempt to keep their heads above water and thereby drown. These biases—which have been briefly described and catalogued in this research paper—involve explicitly defined deviations from the conclusions of valid probabilistic reasoning, which follow from the simplest forms of Bayes’ theorem. They are not random deviations, which could be modeled as analogous to an engineering context involving a ‘signal’ plus ‘noise.’
Of course, we are also capable of precise probabilistic thinking—just as swimmers are capable of assuming a horizontal position in the water and consequently not drowning. The point is, however, that when we deviate from the rules (‘axioms’) of probability theory or from coherent judgments, these deviations follow the patterns described here—as has been documented in everyday observation and studied experimentally by those advocating the ‘heuristics and biases’ approach to such judgment. For a greater elaboration of this approach than is found here, see the chapters in Kahneman et al.’s book Judgment Under Uncertainty: Heuristics and Biases (1982). These systematic departures themselves in turn may be connected to thinking in terms of associations, whereas good probabilistic judgment always requires comparative thinking.
Bibliography:
- Bar-Hillel M 1990 Back to base-rates. In: Hogarth R M (ed.) Insights in Decision Making: A Tribute to Hillel J. Einhorn. University of Chicago Press, Chicago
- Dawes R M 1988 Rational Choice in an Uncertain World. Harcourt Brace Jovanovich, San Diego, CA
- Dawes R M 1994a House of Cards: Psychology and Psychotherapy Built on Myth. Free Press, New York
- Dawes R M 1994b AIDS, sterile needles, and ethnocentrism. In: Heath L, Tinsdale R S, Edwards J, Posavac E, Bryant F B, Henderson-King E, Suarez-Balcazar Y, Myers J (eds.) Social Psychological Applications to Social Issues. III: Applications of Heuristics and Biases to Social Issues. Plenum, New York, pp. 31–44
- Dawes R M 1998 Behavioral decision making and judgment. In: Gilbert D, Fiske S, Lindzey G (eds.) The Handbook of Social Psychology, 11. McGraw-Hill, Boston, MA, pp. 497–548
- Dawes R M 2001 Everyday Irrationality: How Pseudoscientists, Lunatics and the Rest of Us Systematically Fail to Think Rationally. Westview Press, Boulder, CO
- David F N 1962 Games, Gods, and Gambling. Hafner Pub. Co., New York, Chap. 4
- Dawid A P 1982 The well-calibrated Bayesian. Journal of the American Statistical Association 77(379): 605–10
- de Finetti B 1974–5 Theory of Probability: A Critical Introductory Treatment. John Wiley and Sons, London, Vol. 1
- Doherty M E, Mynatt C R, Tweney R D, Schiavo M D 1979 Pseudodiagnosticity. Acta Psychologica 43: 111–21
- Fischhoff B, Beyth-Marom R 1983 Hypothesis evaluation from a Bayesian perspective. Psychological Review 90: 239–60
- Gigerenzer G, Swijtink Z, Porter T, Daston L, Beatty J, Kruger L 1989 The Empire of Chance: How Probability Changed Science and Everyday Life. Cambridge University Press, Cambridge, UK
- Gilovich T, Vallone R, Tversky A 1985 The hot hand in basketball: On the misperception of random sequences. Journal of Personality and Social Psychology 17: 295–314
- Gold E 1997 The Gambler’s Fallacy, Doctoral dissertation submitted in partial fulfillment of the requirement for the degree of Doctor of Philosophy, Carnegie Mellon University
- Hacking I 1975 The Emergence of Probability: A Philosophical Study of Early Ideas About Probability, Induction and Statistical Inference. Cambridge University Press, New York
- Kahneman D, Tversky A 1972 Subjective probability: A judgment of representativeness. Cognitive Psychology 3: 430–54
- Kahneman D, Tversky A 1973 On the psychology of prediction. Psychological Review 80: 237–51
- Kahneman D, Slovic P, Tversky A (eds.) 1982 Judgment Under Uncertainty: Heuristics and Biases. Cambridge University Press, Cambridge, UK
- Meehl P E 1977 Why I do not attend case conferences. In: Meehl P E (ed.) Psychodiagnosis: Selected Papers. W. W. Norton, New York, pp. 225–302
- Meehl P E, Rosen A 1955 Antecedent probability in the efficiency of psychometric signs, patterns, or cutting scores. Psycho-logical Bulletin 52: 194–216
- Mulford M, Dawes R M 1999 Subadditivity in memory for personal events. Psychological Science 10(1): 47–51
- Ramsey F 1931 Truth and probability. In: Ramsey F P (ed.) The Foundations of Mathematics and other Logical Essays. Harcourt, Brace and Co., New York, pp. 156–98
- Russo J E, Schoemaker P J H 1989 Decision Traps: Ten Barriers to Brilliant Decision Making and how to Overcome Them. Simon and Schuster, New York
- Simon H 1955 A behavior model of rational choice. Quarterly Journal of Economics 69: 99–118
- Simon H 1956 Rational choice and the structure of the environment. Psychological Review 63: 129–38
- Simon H 1979 Models of Thought. Yale University Press, New Haven, CT, Vol. 1
- Skov R B, Sherman S J 1986 Information-gathering processes: Diagnosticity, hypothesis-confirmatory strategies, and perceived hypothesis confirmation. Journal of Experimental Social Psychology 22: 93–121
- Summit R C 1983 The child sexual abuse accommodation syndrome. Child Abuse and Neglect 7: 177–93
- Trope Y, Bassok M 1982 Confirmatory and diagnosing strategies in social information gathering. Journal of Personality and Social Psychology 43(1): 22–34
- Tversky A, Kahneman D 1971 Belief in the law of small numbers. Psychological Bulletin 76: 105–110
- Tversky A, Kahneman D 1974 Judgment under uncertainty: Heuristics and biases. Science 185: 1124–31
- von Neumann J, Morgenstern O 1944/1947 The Theory of Games and Economic Behavior, 2nd edn. Princeton University Press, Princeton, NJ
- Wagenaar W 1988 Paradoxes of Gambling Behavior. Lawrence Erlbaum Associates, Hillsdale, NJ
- Wolf F M, Gruppen L D, Billi J E 1985 Differential diagnosis and the competing hypothesis heuristic—a practical approach to judgment under uncertainty and Bayesian probability. Journal of the American Medical Association 235: 2858–62




