Multidimensional Signal Detection Theory Research Paper

1. Introduction And Notation

Stimulus dimensions, A, B,…, represent different types of information about a class of stimuli, for example, in a two-dimensional (2-D) case, the shape (A) and color (B) of objects. The researcher specifies the levels on each dimension to study (e.g., square and rectangle are levels of shape, and blue, turquoise, and green are levels of color). A multidimensional ‘signal’ is stimulus A_iB_j, where the subscript indicates the specific level on the corresponding dimension (e.g., a green square is A₁B₃). For each physical stimulus dimension A (B,…), there is assumed a corresponding unique psychological or perceptual dimension X (Y,…).

The minimal stimulus set considered in this research paper consists of four 2-D stimuli, {A₁B₁, A₁B₂, A₂B₁, A₂B₂}, constructed by combining two levels on dimension A (i = 1, 2) with each of two levels on dimension B ( j = 1, 2). For example, the set constructed from two levels of color (blue, green) and two levels of shape (square, rectangle) is {blue square, blue rectangle, green square, green rectangle}.

On a single trial, one stimulus is selected from the set at random, and it is presented to the observer whose task is to identify the stimulus. The presentation of a 2-D stimulus results in a percept, a point (x, y) in X-Y-perceptual space. The observer’s response is based on the percept’s location relative to the observer’s placement of decision criterion bounds in the perceptual space, typically one bound per dimension, denoted c_A, c_B, … . These bounds divide the perceptual space into response regions such that if, for example, (x, y) falls above c_A and below c_B, the (2-D) response would be ‘21’ (or any response that uniquely identifies it as A₂B₁).

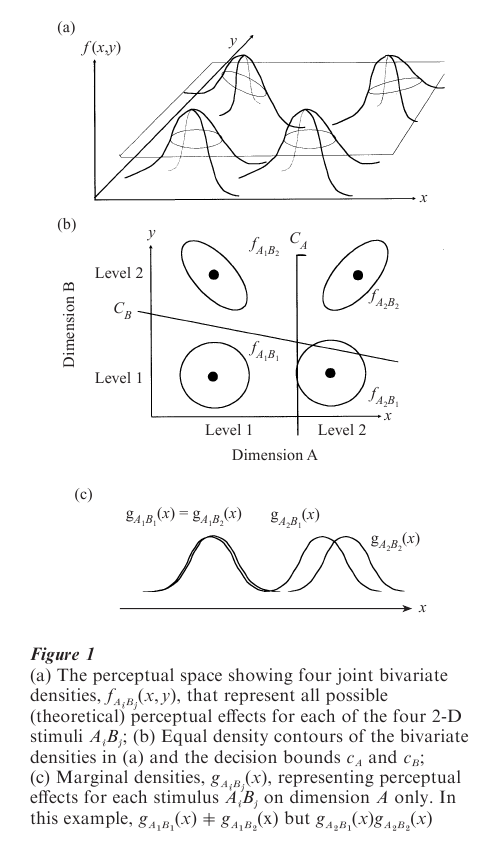
As in unidimensional SDT, multiple presentations of a single stimulus are assumed to lead to a distribution of percepts, and one distribution (usually Gaussian) is assumed for each stimulus. An example with four 2-D stimuli is illustrated in Fig. 1. The bivariate joint densities, f_AiBj(x, y), are represented more easily as equal-density contours (Fig. 1(b)), that are obtained by slicing off the tops of the joint densities in Fig. 1(a) at a constant height, and viewing the space from ‘above.’ The joint density for each stimulus A_iB_j yields: (a) Marginal densities on each dimension, g_AiBj(x) and g_AiBj(y), obtained by integrating over all values of the second dimension (see Fig. 1(c) for marginal densities g_AiBj(x) for dimension A); and (b) Conditional densities for each dimension (not shown), conditioning on the observer’s response to the second dimension, and obtained by integrating only over values either above (or below) the decision bound on the second dimension, for example, g_AiBj(x|y > c_B).

An observer’s responses are tabulated in a 4 × 4 confusion matrix, a table of conditional probability estimates, P(R_p|A_iB_j), that are proportions of trials that response R_p was emitted when stimulus A_iB_j was presented. These proportions estimate the volumes under each joint density in each response region. For example, the proportion of trials on which the observer responded ‘11’ when in fact stimulus A₁B₂ was presented is

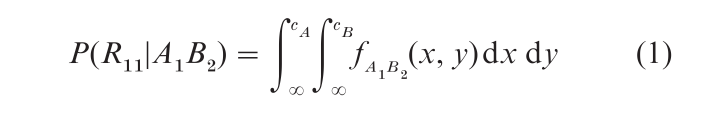
2. Definitions Of Independence Of Dimensions

Several definitions of independence of dimensions are defined within MSDT. These are: perceptual separability (PS), decisional separability (DS), and perceptual independence (PI).

2.1 Perceptual Separability (PS ) And Decisional Separability (DS)

Dimension A is PS from dimension B if the perceptual effects of A are equal across levels of dimension B, that is, g_AiB1 (x) = g_AiB1 (x), for all values of x and both i = 1 and i = 2. Similarly, dimension B is perceptually separable from dimension A if g_A1Bj (x) = g_A1Bj(x), for all y, and j = 1, 2.

DS is a similar type of independence of the decisions that the observer makes about the stimuli. DS holds for dimension A (or B) when the decision bound c_A (or c_B) is parallel to the Y- (or X-) perceptual axis.

PS and DS are global types of independence defined for perceptual dimensions across levels of the second dimension for all stimuli in the set. They can also be asymmetrical relations. In Fig. 1(b), for example, PS holds for dimension B across levels of dimension A, but PS fails for dimension A across levels of B; also, DS holds for dimension A but fails for dimension B.

2.2 Perceptual Independence (PI )

PI is distinguished from PS in that it is a local form of independence among dimensions within a single stimulus. PI holds within stimulus A_iB_j if

for all (x, y). This is statistical independence, and it is a symmetric relation in a given stimulus.

The shape of an equal density contour describes the correlation among the perceived dimensions in one stimulus. A circle indicates PI in a stimulus with variances equal on the two dimensions. An ellipse with its major and minor axes parallel to the perceptual axes also indicates PI, but with unequal variances on the two dimensions. A tilted ellipse indicates failure of PI, with the direction of the tilt (positive or negative slope of the major axis) indicating the direction of the dependence. In Fig. 1(b), stimuli A₁B₁ and A₂B₁ show PI, stimulus A₂B₂ shows a positive dependence, and stimulus A₁B₂ shows a negative dependence.

3. Marginal And Conditional d´s And βs

As in unidimensional SDT, sensitivity, d´, and response bias, β, are parameters that describe different characteristics of the observer. Two sets of these parameters are defined: (a) marginal d´s and βs, and (b) conditional d´s and βs. The marginal and conditional d´s and βs for the four-stimulus set discussed here can be generalized to any number of dimensions and any number of levels: for details, see Kadlec and Townsend (in Ashby 1992, Chap. 8).

3.1 Marginal d´s And βs

Marginal d´s and βs are defined using the marginal densities, g_AiBj(x) and g_AiBj(y). Let the mean vector and variance-covariance matrix of f_AiBj(x, y), for stimulus A_iB_j, be denoted by

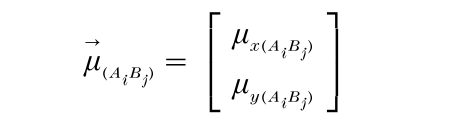
and

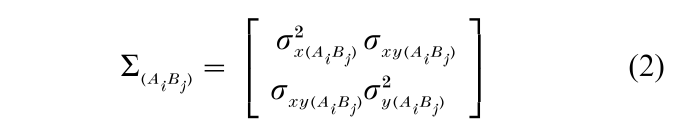
respectively. The marginal d for dimension A at level j of dimension B is

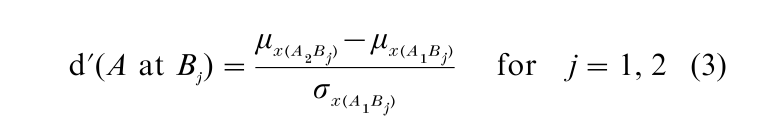
The subscript x indicates that for a d on dimension A, only the X-coordinates of the mean vectors and the standard deviation along the X-perceptual axis are employed. As in unidimensional SDT, the standard deviation of the ‘noise’ stimulus (here indicated as level 1 of dimension A) is used, and without loss of generality, it is assumed that µ_(A1B1) = [0 0]^T(^Tdenotes transpose) and Σ_(A1B1) = I (i.e., σ_x² = σ_y² = 1, and σ_xy = 0). Similarly, the marginal d s for dimension B at level i of dimension A is

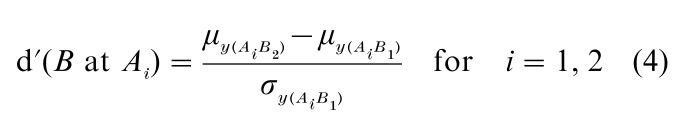
In a parallel fashion, marginal βs are defined as

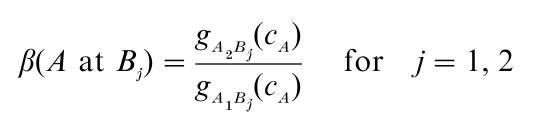
and

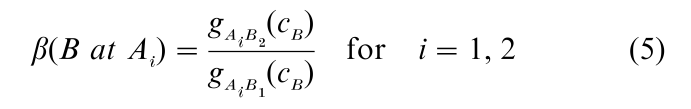
where c_A and c_B are the decision bounds for dimension A and B, respectively.

3.2 Conditional d´s And βs

In the four-stimulus set, two pairs of conditional d´s and βs are defined for each dimension, conditioning on the observer’s response on the second. Using the terminology of unidimensional SDT for simplicity, with level 1 indicating the ‘noise’ stimulus and level 2 the ‘signal’ stimulus, one pair of conditional d´s for dimension A, with B presented at level 1, is: (a) d (A ‘correct rejection’ on B)—conditioned on the observer’s correct response that B was at level 1, defined using parameters of

i = 1 and 2 in Eqn. (3); and (b) d´(A ‘false alarm’ on B)—conditioned on the incorrect response that B was at level 1, using parameters of

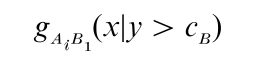
in Eqn. (3). The second pair of conditional d´s for dimension A, with B presented at level 2, is: (c) d´(A|‘hit’ on B)—conditioned on the correct response that B was at level 2; and (d) d´(A|‘miss’ on B)—conditioned on the incorrect response that B was at level 1. Similar pairs are defined for conditional βs, and for d´s and βs for dimension B conditional on dimension A responses.

4. Using The d´s And βs To Test Dimensional Interactions

These d´ and β parameters are linked theoretically to PS, DS, and PI (Kadlec and Townsend 1992). Their estimates, obtained from the confusion matrix proportions (Eqn. (1)), can thus be used to draw tentative inferences about dimensional interactions (Kadlec 1999). DS for dimension A (or B) is inferred when c_A (c_B) estimates are equal at all levels of dimension B (A). Equal marginal d s for a dimension across levels of the other are consistent with PS on that dimension. A stronger inference for PS on both dimensions can be drawn if the densities form a rectangle (but not a parallelogram), and this condition is testable if DS and PI hold (Kadlec and Hicks 1998; see also Thomas 1999 for new theoretical developments). When DS holds, evidence for PI is gained if conditional d s are found to be equal: Conversely, unequal conditional d s indicate PI failure, and the direction of the inequality provides information about the direction of the dimensional dependencies in the stimuli. Exploring these relationships and looking for stronger tests of PS and PI is currently an active area of research.

MSDT is a relatively new development, and with its definitions of independence of dimensions, it is a valuable analytic and theoretical tool for studying interactions among stimulus dimensions. Current applications include studies of (a) human visual perception (of symmetry, Gestalt ‘laws’ of perceptual grouping, and faces); and (b) source monitoring in memory. It can be used in any research domain where the study of dimensional interactions is of interest.

Bibliography:

1. Ashby F G (ed.) 1992 Multidimensional Models of Perception and Cognition. Hillsdale, Erlbaum, NJ
2. Ashby F G, Maddox W T 1994 A response time theory of separability and integrality in speeded classification. Journal of Mathematical Psychology 38: 423–66
3. Ashby F G, Townsend J T 1986 Varieties of perceptual independence. Psychology Review 93: 154–79
4. Kadlec H 1999 MSDA-2: Updated version of software for multidimensional signal detection analyses. Behavior Research Methods, Instruments & Computers 31: 384–5
5. Kadlec H, Hicks C L 1998 Invariance of perceptual spaces. Journal of Experimental Psychology: Human Perception & Performance 24: 80–104
6. Kadlec H, Townsend J T 1992 Implications of marginal and conditional detection parameters for the separabilities and independence of perceptual dimensions. Journal of Mathematical Psychology 36: 325–74
7. Thomas R D 1999 Assessing sensitivity in a multidimensional space: Some problems and a definition of a general d´. Psychonomic Bulletin & Review 6: 224–38