Geometry Of Visual Space Research Paper

1. Is Visual Space Non-Euclidean?

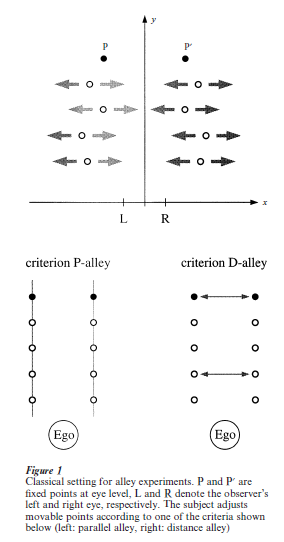
The question of whether visual space is Euclidean was not formulated explicitly until the beginning of the twentieth century. Answers to this question, however, can be traced back as far as the ancient Greek philosophers. Suppes (1997) presents a list of classical contributions to this problem, starting with Euclid’s theory of perspective (rated as a ‘Yes’ answer). His list contains a majority of ‘No’ statements, some undecided cases rated as ‘not sure,’ and only a few ‘Yes’ conclusions, mainly from authors using philosophical arguments rather than empirical results. Strong evidence against Euclidean geometry as an appropriate description of the structure of visual space arose from observations in so-called alley experiments. Investigating the phenomenon of size constancy, Hillebrand (1902, cited in Lukas 1996) asked subjects to arrange small light points in the horizontal plane along two lines such that they should form an alley-like configuration, running from two fixed points towards the observer. He used two similar tasks but with different instructions. The first was to match the ‘horizontal distances’ of points to make sure that, perceptually, the width of the alley should be perceived as equal at any egocentric distance (D-alley).

The second was to pay attention to the alley’s right and left border and make sure that they are perceived as ‘parallel straight lines’ (P-alley). To Hillebrand’s surprise, the two instructions led to different configurations. Both alley types were curved, with Dalleys consistently lying ‘outside’ the corresponding P-alleys (see Fig. 1). Blumenfeld (1913, cited in Lukas 1996) confirmed this finding and was the first to mention a far-reaching consequence: since in Euclidean geometry lines with constant distance everywhere are called parallel (and vice versa), visual space has to be non-Euclidean. Blumenfeld’s geometric reasoning elicited a vivid discussion, but for more than 30 years thereafter, it was not worked out mathematically in any substantive way. Luneburg (1947) was the first to present both a complete geometrical framework for visual space, and explicit psychophysical functions that related physical and visual coordinates in order to explain the striking results of the alley experiments and other empirical facts in binocular space perception known at that time.

2. Geometry As A Mathematical Language For Spatial Structure

Within mathematics there are at least two different approaches to geometry, the ‘synthetic’ and the ‘analytic’. In the spirit of Euclid’s axiomatic approach, synthetic geometry is defined over a set of points and a set of straight lines as primitives by specifying a number of relations considered to be true. Over many centuries Euclid’s axioms have been considered to be the only reasonable description for spatial relationships. They include incidence axioms (for example, any two distinct lines have at most one common point), order axioms, axioms concerning motion and congruity, metric axioms, and, finally, the famous parallel axiom stating that for any point P and any line g not containing P there is one and only one line g through P parallel to (not intersecting) g. At the beginning of the nineteenth century, however, Gauss, Bolyai, and Lobachevski discovered independently that the parallel axiom can be replaced by the postulate that there exist at least two parallels, yielding a different type of geometry (later called ‘hyperbolic’). Moreover it has been shown that even a third version of the parallel axiom, stating that any two lines have at least one point in common, is compatible with the remaining Euclidean axioms, and leads to an ‘elliptic’ geometry.

The properties of both types of non-Euclidean geometry are demonstrated easily by models that fulfill the respective set of axioms. A well-known model for an elliptic plane is the surface of a sphere in Euclidean space IR², where the set of elliptic lines is defined as the set of all (Euclidean) great circles. Similarly, models for hyperbolic geometry can be constructed on surfaces with constant negative curvature in IR² (for example, saddle-shaped surfaces). Hyperbolic geometry is therefore said to have constant negative curvature, whereas elliptic geometry is characterized by its constant positive curvature.

3. Theories On The Geometry Of Visual Space

Let V be the set of all points in the three-dimensional physical space which a fixed observer can see without moving the head. If x, y, z denote the Euclidean coordinates in physical space, then V is a subset of the positive half space y > 0 right in front of the observer. The origin of the coordinate system is interpreted as the egocenter of the observer and is assumed to lie in the closure of V, the x-axis denotes the direction from left to right, and the z-axis corresponds to the vertical axis. We restrict the following discussion to the horizontal plane z = 0 at eye level. The well-known Euclidean metric d_phys represents the physical distances in V.

In his famous attempt to represent the perceptual structure of binocular visual space geometrically, Luneburg (1947) starts out with the basic assumption that in addition to d_phys there exists some metric d_vis on V that represents the ‘perceived’ spatial structure. If γ and φ denote binocular parallax and bipolar latitude, respectively, his theory can be summarized by the following basic hypotheses:

LH 1             There exists a Riemannian metric d_vis on the visual field V that represents perceived

distances. The geodesics of d_vis are perceived as straight lines.

LH 2 The visual space (V, d_vis) has constant

Gaussian curvature K.

LH 3 The perceived distance d_vis (0, P) of

point P to the observer is a function of the

bipolar parallax only.

LH 4 The φ-translations (γ, φ) → (γ, φ + const) are

visual isometries (leave all perceived

distances unchanged).

LH 5 The γ-translations (γ, φ) → (γ + const, φ) are

angle-preserving.

Assumption LH 1 provides the basis for the remaining assumptions: In a Riemannian metric space a coordinate system can be introduced that allows numerical representations for any geometrical objects such as lines, angles, triangles, or distances. LH 2 restricts the discussion to geometries that are constantly curved everywhere. The remaining assumptions LH 3 through LH 5 define the psychophysical relationship between (physical) stimulus space and (perceptual) visual space. LH 3 implies, for example, that points lying on a Vieth–Muller circle (a circle containing the nodal points of the observers eyes) are perceived as equidistant to the observer because they have the same bipolar parallax γ. These latter assumptions are explained and discussed extensively in Binocular Space Perception Models.

Eschenburg (1980) gave a complete proof of Luneburg’s conjecture that LH 1 through LH 5 uniquely determine the metric d_vis by two parameters K and σ up to equivalence. More specifically, the line element of the metric is represented in terms of the bipolar coordinates φ and γ by

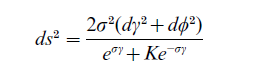
(Eschenburg 1980 p. 7). K denotes the Gaussian curvature of visual space, and σ is an individual scaling factor.

4. Empirical Results On Geometrical Structures Of Visual Space

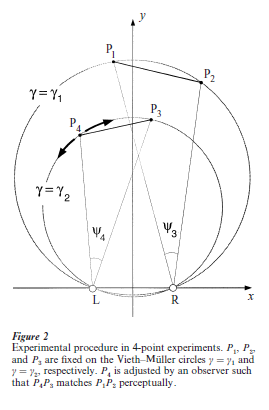
Whereas LH 3 through LH 5 are closely connected to the psychophysical relationship between physical and visual coordinates, LH 1 and LH 2 define the inner geometry of visual space. Empirical investigations have concentrated on two questions: (a) is K constant? (b) if so, is K = 0 indicating Euclidean geometry, or K < 0 (hyperbolic geometry) or K > 0 (elliptic space)? The early observations of distance alleys lying consistently outside the corresponding parallel alleys are only compatible with hyperbolic geometries (Indow and Watanabe 1984). Direct numerical estimates for K can be derived from alley experiments or from so-called 3and 4-point experiments using double Vieth–Mullercircles (VMC) suggested by Luneburg (1947) (see Fig. 2). Using these methods K has mostly been found to be negative (Hardy, Blank, Boeder, Rand, and Rittler, 1953, cited in Lukas 1996). However, numerical estimates of K cannot always reliably be reproduced in repeated measurements, estimates resulting from 3and 4-point experiments are not valid predictors for data obtained from alley experiments, and experiments over large egocentric distance ranges coincide qualitatively but not quantitatively (Indow 1991).

Moreover, for a test of LH 2, numerical estimates of K are only of limited utility, because they presuppose the psychophysical mapping functions. Several methods have been suggested to test LH 1 and LH 2 independently from the remaining assumptions. In the triangle method used by Blank (1961) subjects had to bisect two sides of a given triangle ABC. Six of a total of seven subjects gave judgments indicating a negative curvature. However, the results seem to depend on the size of the triangle. Using the same method, Higashiyama (1981) found strong variations in curvature depending on lateral positions of the triangles and their distance from the observer. Battro et al. (1976) used stakes to produce experimental alleys of variable size in large open fields in natural environments. The curvature of visual space did not show a negative constant value. In addition, the results of experiments with equidistant lines and visual triangles under these viewing conditions also invalidated the constant curvature assumption.

Luneburg (1947) used quite a different argument and referred to the fact that Riemannian spaces with constant curvature are often characterized geometrically by a property called free mobility (any con- figuration can be moved to any position in space without changing the shape). Eschenburg (1980) showed that, contrary to Luneburg’s argumentation, the existence of visual isometries alone does not guarantee free mobility in a strict sense. In Blank’s (1958, cited in Blank 1961) axiomatic version of Luneburg’s theory, free mobility is guaranteed by an axiom that implies both the so-called Desarguesian property, and constant curvature in Riemannian spaces. Empirical consequences of this axiom have been tested successfully by Foley (1964, cited in Foley 1972). However, a much stronger test in subsequent experiments failed (Foley 1972). Lukas (1996) gave detailed arguments as to why the first test might have been too weak and the latter one unreasonably strong. From an empirical point of view Eschenburg (1980) provides the most powerful and sensitive test of the constant curvature hypothesis. He shows that an appropriate combination of the double VMC- experiments produces necessary and sufficient conditions for LH 2. Experimental tests of these conditions reported in Lukas (1996) reflect a situation that seems to characterize most results in this field: the data are nicely fitted qualitatively by the predictions using constant curvature, yet there are numerically small, but statistically significant deviations.

Nevertheless, there are few models in the literature that try to generalize Luneburg’s geometrical assumptions (contrary to his psychophysical assumptions, which have been relaxed in several attempts). Yamazaki (1987) developed a concrete non-Riemannian geometry and suggested its application to visual space. Because this model does not use the concept of length, its utility for empirical research seems limited.

A different approach is reported in Lukas (1996). Starting out with an axiomatic analysis of size constancy, he defines ‘apparent distance’ in terms of modern measurement and shows that a very weak invariance condition resembling Luneburg’s iseiconic transformations (defined in LH 4 and LH 5) forces the geometric structure of visual space to be Euclidean.

5. Conclusion And Future Directions

Critical reviews of empirical results seem to indicate that there is little hope of characterizing visual space globally by one particular geometry. Suppes (1995) concludes that visual space is context-dependent and no reasonable simple set of axioms in the spirit of synthetic geometry can be given for the structure of visual space. This view seems to be supported by recent results from Zimmer (1998). In a series of experiments, subjects failed in a test of very basic requirement of ‘betweenness’ indicating that not even simple order structures on a straight line can be assumed to hold a priori. Nowadays, geometric models in visual perception are actively discussed almost exclusively in the context of mathematical psychology and foundational aspects of science. The main stream of research in vision has obviously shifted to computational models and the analysis of cognitive processes underlying human performance in spatial perception.

Bibliography:

1. Battro A M, di Pierro Netto S, Rozestraten R J 1976 Riemannian geometries of variable curvature in visual space: Visual alleys, horopters, and triangles in big open fields. Perception 5: 9–23
2. Blank A A 1961 Curvature of binocular visual space. Journal of the Optical Society of America 51: 335–9
3. Eschenburg J H 1980 Is binocular visual space constantly curved? Journal of Mathematical Biology 9: 3–22
4. Foley J M 1972 The size–distance relation and intrinsic geometry of visual space: Implications for processing. Vision Research 12: 323–32
5. Higashiyama A 1981 Variation of curvature in binocular visual space estimated by the triangle method. Vision Research 21: 925–33
6. Indow T 1991 A critical review of Luneburg’s model with regard to global structure of visual space. Psychological Review 98: 430–53
7. Indow T, Watanabe T 1984 Parallel and distance alleys with moving points in the horizontal plane. Perception and Psychophysics 35: 144–54
8. Lukas J 1996 Psychophysik der Raumwahrnehmung. Psychologie Verlags Union, Weinheim, Germany
9. Luneburg R K 1947 Mathematical Analysis of Binocular Vision. Technical Report, Princeton, NJ
10. Suppes P 1977 Is visual space Euclidean? Synthese 35: 397–421
11. Suppes P 1995 Some foundational problems in the theory of visual space. In: Luce R D, D’Zmura M, Hoffman D D, Iverson G J, Romney A K (eds.) Geometric Representations of Perceptual Phenomena: Papers in Honor of Tarow Indow on his 70th Birthday. Lawrence Erlbaum Associates, Mahwah, NJ
12. Yamazaki T 1987 Non-Riemannian approach to geometry of visual space: An application of affinely connected geometry to visual alleys and horopter. Journal of Mathematical Psychology 31: 270–98
13. Zimmer K 1998 Experimentelle Untersuchungen zur Geometrischen Struktur des Binokularen Sehraums. Shaker, Aachen, Germany