Karl Pearson Research Paper

1. Career

Karl Pearson was proud that his ancestors were of ‘yeoman stock’ though his father was a barrister. At Cambridge Karl read mathematics. Third place in the examinations brought him a college fellowship and the financial freedom to pursue his very wide interests. Pearson qualified as a barrister and studied social, philosophical, and historical issues. He developed his own view of man’s place in a post-Christian world, expressing this in a novel and a play as well as through essays; some of those were published in the Ethic of Freethought (1888).

In 1884 the essayist and freelance lecturer became professor of Applied Mathematics and Mechanics at University College London. Besides carrying out the usual duties, Pearson took on two books left un-finished when their authors died. W. K. Clifford’s Common Sense of the Exact Sciences explained the nature of mathematics and it would link Pearson’s early general essays to the Grammar of Science (1892). The Grammar of Science presented the scientific method as ‘the orderly classification of facts followed by the recognition of their relationship and recurring sequences.’ In later editions the positivist ideas about space and force were joined by an exposition of statistical ideas. The other book, Isaac Todhunter’s History of the Theory of Elasticity, was the history of Pearson’s own specialism. Pearson actually wrote much more of this huge work than Todhunter himself. Pearson’s later historical researches—a biography of Galton and lectures on the history of statistics—com- bined Todhunter’s thoroughness with Pearson’s own very different awareness of broad intellectual currents.

Pearson moved from elasticity and philosophy to biometry and statistics under the influence of W. F. R. Weldon, appointed to the college in 1890 as professor of Zoology. Weldon was applying Galton’s statistical methods to species formation and Pearson helped him extend the methods. However, Pearson was not just a mathematical consultant, he became a contributor to the biological literature in his own right. The partnership with Weldon was central to Pearson’s development and he made his most important contributions to statistical thinking in these early years with Weldon. Pearson wrote over 300 pieces after 1900 but they were on lines he had already established. Of course these works demonstrated what statistical methods could achieve and were part of making statistics a recognized discipline.

In 1901 Pearson, Weldon and Galton founded Biometrika, a ‘Journal for the Statistical Study of Biological Problems’ which also published tables and statistical theory. From 1903 a grant from the Worshipful Company of Drapers funded the Biometric Laboratory. The laboratory drew visitors from all over the world and from many disciplines. Pearson wrote no textbook or treatise but the visitors passed on what they had learnt when they returned home. In 1907 Pearson took over a research unit founded by Galton and reconstituted it as the Eugenics Laboratory. This laboratory researched human pedigrees but it also produced controversial reports on the role of inherited and environmental factors in tuberculosis, alcoholism, and insanity—great topics of the day. In 1911 a bequest from Galton enabled Pearson finally to give up responsibility for applied mathematics and become Professor of Eugenics and head of the Department of Applied Statistics. During World War One, normal activities virtually ceased but afterwards expansion was resumed. However, Pearson was no longer producing important new ideas and Ronald Fisher was supplanting him as the leading figure in statistics. Pearson retired in 1933 but he continued to write and, with his son Egon. vs. Pearson, to edit Biometrika.

Pearson made strong friendships, notably with Weldon and Galton. He also thrived on controversy. Some of the encounters produced lasting bitterness, those with William Bateson and Ronald Fisher being particularly unforgiving. Following the ‘rediscovery’ of Mendel’s work in 1900, Bateson questioned the point of investigating phenomenological regularities such as Galton’s law of ancestral heredity. The biometricians replied that such regularities were established and that any theory must account for them. After Weldon’s death in 1906, the biometricians were often miscast as mathematicians who knew no biology. The quarrel about the value of biometric research faded with Bateson’s death and Pearson’s withdrawal from research into inheritance. Fisher, like Bateson, was a Mendelian but there was no quarrel about the value of statistics. Fisher criticized the execution of Pearson’s statistical work but he also considered himself a victim of Pearson’s abuse of his commanding position in the subject.

2. Contributions To Statistics

Pearson was a tireless worker for whom empirical research and theoretical research went hand in hand. His empirical work was always serious. He wanted to make a contribution to knowledge in the field to which he was applying his methods not just to show that they ‘worked,’ but so he would set out to master the field. However, his contribution to statistical methodology overshadowed his contribution to any substantive field. His statistical contributions can be divided into ways of arranging numerical facts—univariate and multivariate—and methods of inference—estimation and testing.

3. Univariate Statistics: The Pearson Curves

Pearson’s first major paper (1894) was on extracting normal components from ‘heterogeneous material.’ However, Pearson considered ‘skew variation in homogeneous material’ a more serious problem for he held that the normal distribution underlying the theory of errors was seldom appropriate. Pearson (1895) presented a system of frequency curves; these would be of use in ‘many physical, economic and biological investigations.’ Systems were also developed by Edgeworth, Charlier, Kapteyn, and others, but Pearson’s was the most widely used. Other systems have been devised, inspired by his, but none has been as central to the statistical thought of its time.

From probabilistic considerations—which now seem contrived—Pearson obtained a basic differential equation governing the probability density function, or frequency curve, y = y(x):

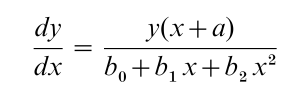
The constants determine the form of the curve. Pearson developed methods for choosing an appropriate curve and for estimating the constants. His laboratory produced tables to ease the burden of calculation.

While Pearson used these curves as data distributions, he assumed that the estimators of the constants would be approximately normal, certainly in large samples. In the work of ‘Student’ (W. vs. Gosset) and then Fisher the data distributions are normal but the exact distributions of the sample statistics are usually not, though they may follow the Pearson curves. ‘Student’ did his distribution work in Pearson’s laboratory but for many years Pearson thought that such ‘small sample’ work was off the main track and useful only to ‘naughty brewers.’

In the Pearson system the normal distribution is just one type. In Fisher’s analysis of variance which appeared in the 1920s it is the only type. People schooled in the Pearson system did the earliest robustness studies and one of the continuing roles of the system has been in this area. While Pearson’s skepticism towards normality pervades much modern work, the modern approach to inference is so different from his that he is not a direct inspiration.

4. Multivariate Statistics: Correlation And Contingency

In 1888 Galton introduced correlation and soon Edgeworth was developing the theory and Weldon was applying the method in his research on crustaceans. Pearson, however, produced the definitive formulation of normal correlation and had the vision that correlation would transform medical, psychological, and sociological research.

Pearson (1896) set out to frame hypotheses about inheritance in terms of the multivariate normal distribution but these were of less enduring interest than his account of correlation and multiple regression. The familiar partial and multiple correlation and regression coefficients appear at this time either in Pearson’s work or that his assistant, G. Udny Yule. Soon Pearson and those around him were applying correlation in meteorology, sociology and demography as well as in biometry.

The 1896 ideas formed the basis of a definitive theory, especially when completed by the exact distribution theory of ‘Student’ and Fisher. But Pearson soon moved on to qualitative, non-normal, and time series data, though not with the same success. Pearson’s scheme for contingency, the qualitative analogue of correlation, has latent continuous variables—surprisingly jointly normal ones. Yule, no longer working with him, rejected the scheme. The controversy that ensued had no clear resolution. Pearson toiled unsuccessfully to create a theory of skew surfaces, uniting correlation and skew curves. Time series correlation analysis was another disputed field. Pearson thought of the true correlation between series as obscured by time trends superimposed upon them. The scheme was widely used but in the 1920s Yule criticized it effectively, yet putting nothing in its place.

From the beginning Pearson encountered problems with correlation which have lived in the underworld of statistics occasionally surfacing in fields such as path analysis and structural modeling. Pearson formalized Galton’s notion of correlation as measuring the extent to which variables are governed by ‘common causes.’ He was soon aware of cases of ‘spurious correlation’ where the natural interpretation is not sustainable. He and Yule—who developed the other standard interpretation of a direct causal relationship between the correlated variables—found numerous pathological cases. They devised treatments but developed no systematic way of thinking about the problem.

Pearson—following Galton—established multivariate analysis. Yet by a curious twist the multivariate data for which Pearson struggled to create a theory of frequency surfaces is often treated by Fisher’s ‘regression analysis’ which was a development from Gauss’s univariate theory of errors rather Pearson’s correlation theory.

5. Estimation: The Method Of Moments And Inverse Probability

Pearson usually found the constants of frequency curves by the method of moments. He introduced this in his first major paper (1894) for he could find no other method for estimating a mixture of normals. Pearson went on to apply the method quite generally. It seemed particularly appropriate for the Pearson curves where the constants determine the first four moments. However, the method was put on the defensive after Fisher criticized it for not being ‘efficient’—even when applied to the Pearson curves.

Probable errors (scaled standard errors corresponding to the 50 percent point) for method of moments estimators were derived by Pearson and Filon (1898) using a modification of an argument in the 1896 correlation paper. Pearson had obtained the productmoment estimate from the posterior distribution (based on a uniform prior) and its probable error from a large sample normal approximation to the posterior. In 1898 he assumed that the same technique would always yield probable errors for the method of moments. He seems to have dropped the technique when he realized that the formulae could be wrong but it was reshaped by Fisher into the large sample theory of maximum likelihood.

In 1896/8 Pearson used Bayesian techniques in a formalistic way but he could be a thoughtful Bayesian. Over a period of 30 years he wrote about the ‘law of succession,’ the standard Bayesian treatment of predicting the number of successes in future Bernoulli trials given the record of past outcomes—‘the fundamental problem of practical statistics’ he called it. Pearson held that a prior must be based on experience; a uniform prior cannot just be assumed. Pearson pressed these views in estimation only once when he criticized Fisher’s maximum likelihood as a Bayesian method based on an unsuitable prior—essentially Pearson’s own method of 1896 8. Fisher was offended by this misinterpretation of his Bayes-free analysis.

There was plenty of improvisation in Pearson’s estimation work; it was eclectic, even inconsistent. He was not the consistent Bayesian that Jeffreys would have liked. Pearson used sampling theory probable errors but he did not follow up the results on the properties of estimators in the old theory of errors. Pearson was not unusual in his generation; the theory of errors he found to hand-mixed frequentist and Bayesian arguments. Some of his contemporaries were more acute but foundational clarity and integrity only became real values towards the end of his career when Fisher, Jeffreys, and Neyman set about eliminating the wrong kind of argument.

6. Testing: Chi-Squared

Pearson’s earliest concerns were with estimation— curve fitting and correlation—though there testing could be done, using the estimates and their probable errors and making the assumption of large sample normality. However, his chi-squared paper of 1900 introduced a new technique and gave testing a much bigger role.

The chi-squared test made curve fitting less subjective. One could now say: ‘In 56 cases out of a hundred such trials we should on a random selection get more improbable results than we have done. Thus we may consider the fit remarkably good.’ The tail area principle was adopted without any examination. Naturally Pearson enjoyed showing that the fit of the normal distribution to errors in astronomical measurements was not good.

Pearson brought chi-squared into his treatment of contingency and by 1916 he had established the main applications of the chi-squared distribution—a test for goodness of fit of distributions, a test for independence in contingency tables, a test for homogeneity of samples, a goodness of fit test for regression equations.

Pearson’s distribution theory involved the exact distribution of the exponent in the multinormal density, this density appearing as a large sample approximation to the multinomial. Pearson slipped in the mathematics and used the same approximation whether the constants of the frequency curves are given a priori or estimated from the data. Fisher realized the importance of the difference and reconstructed the theory, finding that the chi-squared approximation was valid but the number of degrees of freedom had to be altered.

Fisher continued Pearson’s chi-squared work and gave significance testing an even bigger role in applied statistics. Pearson’s methods were more or less vindicated by the later work of Fisher and then of Neyman and E. vs. Pearson but, as in estimation, his reasons did not pass critical examination.

7. Summary

Of the many statistical techniques Pearson devised, only a few remain in use today and though his ideas sometimes find re-expression in more sophisticated form, such as the correlation curve or the generalized method of moments, there is little to suggest that Pearson continues to directly inspire work in statistics.

Pearson broke with the theory of errors but in the next generation through the analysis of variance and regression the theory was restored to stand beside, even to overshadow, Pearsonian statistics. From a modern perspective Pearson’s theory seems desperately superficial. Yet the problems he posed have retained their importance and the ground he claimed for the discipline of statistics has not been given up. Pearson was an extraordinarily prolific author and there is also a considerable secondary literature. There is a brief guide to this literature on the website http://www.soton.ac.uk/jcol

Bibliography:

1. Eisenhart C 1974 Karl Pearson. Dictionary of Scientific Biography 10: 447–73
2. Hald A 1998 A History of Mathematical Statistics from 1750 to 1930. Wiley, New York
3. MacKenzie D A 1981 Statistics in Britain 1865–1930: The Social Construction of Scientific Knowledge. Edinburgh University Press, Edinburgh, UK
4. Magnello M E 1999 The non-correlation of biometrics and eugenics: Rival forms of laboratory work in Karl Pearson’s career at University College London, (in two parts). History of Science 37: 79–106, 123–150
5. Morant G M 1939 A Bibliography: of the Statistical and other Writings of Karl Pearson. Cambridge University Press, Cambridge, UK
6. Pearson E S 1936/8 Karl Pearson: An appreciation of some aspects of his life and work, in two parts. Biometrika 28: 193–257; 29: 161–247
7. Pearson K 1888 The Ethic of Freethought. Fisher Unwin, London
8. Pearson K 1892 The Grammar of Science [further editions in 1900 and 1911]. Walter Scott, London [A.& C Black, London]
9. Pearson K 1894 Contributions to the mathematical theory of evolution. Philosophical Transactions of the Royal Society A. 185: 71–110
10. Pearson K 1896 Mathematical contributions to the theory of evolution. III. Regression, heredity and panmixia. Philosophical Transactions of the Royal Society A. 187: 253–318
11. Pearson K, Filon L M G 1898 Mathematical contributions to the theory of evolution IV. On the probable errors of frequency constants and on the influence of random selection on variation and correlation. Philosophical Transactions of the Royal Society A. 191: 229–311
12. Pearson K, Filon L M G 1900 On the criterion that a given system of deviations from the probable in the case of correlated system of variables is such that it can be reasonably supposed to have arisen from random sampling. Philosophical Magazine. 50: 157–75
13. Pearson K, Filon L M G 1914/24/30 The Life, Letters and Labours of Francis Galton. Cambridge University Press, Cambridge, UK, Vols. I, II, IIIA, IIIB
14. Provine W B 1971 The Origins of Theoretical Population Genetics. Chicago University Press, Chicago
15. Semmel B 1960 Imperialism and Social Reform: English Social-Imperial Thought 1895–1914. George Allen & Unwin, London
16. Stigler S M 1986 The History of Statistics: The Measurement of Uncertainty before 1900. Belknap Press of Harvard University Press, Cambridge, MA